SiSy_HS12_sempruef

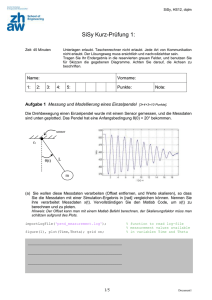
SiSy, HS12, dqtm
SiSy Semester-Prüfung:
Zeit: 90 Minuten
Unterlagen erlaubt. Taschenrechner nicht erlaubt. Jede Art von Kommunikation
nicht erlaubt. Der Lösungsweg muss ersichtlich und nachvollziehbar sein.
Tragen Sie Ihr Endergebnis in die reservierten grauen Felder, und benutzen Sie
für Skizzen die gegebenen Diagramme. Achten Sie darauf, die Achsen zu
beschriften.
Name:
1:
2:
Vorname:
3:
4:
5:
Punkte:
Note:
Aufgabe 1 Chapter 1 Introduction, Signals & Matlab-Plots [4x4=16 Punkte].
(a) Vervollständigen Sie den Matlab Code, welchen den unteren Graph erzeugt.
clear all, close all, clc;
N = 16;
% Anzahl Punkte
n = _________________
x_n = __________________
stem(n,x_n)
…
1/10
Document1
SiSy, HS12, dqtm
Zeichnen Sie die Graphen unten, welche mit folgendem Matlab-Code erzeugt werden.
(b) Figure-1
clear all, close all, clc
Tau = 0.01;
tstep = Tau/20;
t = 0:tstep:5*Tau;
yb_t = (1/Tau)*(exp(-t/Tau));
figure(1), plot(t,yb_t)
…
% Numerische Approximation
% der Integral-Operation
yc_t = tstep*cumsum(yb_t);
figure(2)
plot(t,yc_t)
…
(c) Figure-2
(d) Berechnen Sie das Integral unten
und bestimmen Sie den Endwert für
ihre Kurve im Teilaufgabe (c).
t
 y   d  ?
b
0
(Platz für die Berechnung von Teilaufgabe-d)
2/10
Document1
SiSy, HS12, dqtm
Aufgabe 2 Chapter 2 :Reference Systems
[5+3=8 Punkte].
Der Frequenzgang G(jω) eines typischen Systems (Tiefpassfilters 2te Ordnung mit Parametern
k, ω0 und d ) ist unten gegeben.
G  j  
k 02
 j 2  2d 0  j    02
k  1

d  0,1
  1M rad s  10 6 rad s
 0
(a) Es werden unten zwei passive RLC Topologien gegeben. Mit welcher kann man ein TPF
wie oben realisieren? Begründen Sie ihre Antwort mit einem Vergleich des Frequenzganges
und bestimmen Sie die Werte von L und C, gegeben ist R =10kΩ.
TOPOLOGIE-A
TOPOLOGIE-B
Notation:
s   j 
Topologie:
L=
C=
(b) Welcher Typ von Filter wird realisiert mit der anderen Topologie? Vergessen Sie nicht ihre
Antwort zu begründen (z.Bsp. mit einer Skizze des Amplitudengangs).
Filter-Typ:
3/10
Document1
SiSy, HS12, dqtm
Aufgabe 3 Chapter 2 System Views Darstellungsarten
[4+2=6 Punkte].
Das Blockschaltbild eines Systems ist unten gegeben.
A0
- m t 
u(t)
B0
+

m t 
y t 
+
-
yt 

y(t)
A1
(a) Berechnen Sie die entsprechende Differentialgleichung (DGl), welche das System
vollständig beschreibt. In ihrer DGl sollen nur Termen mit u(t), y(t) und entsprechende
Ableitungen vorkommen.
 t  und y t  beschreiben und dann
Hinweis: Bestimmen Sie zuerst die zwei DGl, welche m
überlegen Sie sich, wie Sie die gesammte DGl ausrechnen können.
DGl:
(b) Zeigen Sie mit einer Berechnung, dass der Frequenzgang G(jω) dem obigen System
gleicht:
G j  
B0
 j 2  A1   j   A0
Bmk: So können Sie ihr Ergebnis von Teilaufgabe (a) verifizieren.
4/10
Document1
SiSy, HS12, dqtm
Aufgabe 4 Chapter 2 System : Convolution (Faltung)
[6+3=9 Punkte].
(a) Zwei diskrete Signale u[n] und g[n] sind unten gezeichnet. Berechnen und skizzieren Sie
das Signal y[n] definiert als: yn  un gn
Bmk: Ihr Lösungsweg (Berechnung mit Tabelle, Skizze oder Gleichungen muss ersichtlich
sein).
(b) Eine Audioaufnahme (Signal u[n] unten) und ein diskretes Signal y[n] wie unten gezeichnet
(siehe 2te Graph unten) werden miteinander gefaltet. Welcher Effekt wird dadurch erzeugt?
Begründen Sie ihre Antwort mit einer Aussage und/oder einer Skizze/Gleichung.
5/10
Document1
SiSy, HS12, dqtm
Aufgabe 5 Chapter 3 FR : Spectrum Introduction und FR-Notations
[3+4=7 Punkte].
Das einseitige Spektrum eines Signals x(t) wird gemessen und ist unten gezeichnet.
Ak
3/2
1
0
15
30
45
60
f [Hz]
15
30
45
60
f [Hz]
k
+/2
0
-/2
-
(a) Bestimmen Sie die Gleichung x(t) (als Summe von allen harmonischen Anteilen) :
Bmk: Achten Sie auf den DC-Inhalt.
x(t) =
(b) Bestimmen Sie die Koeffizienten ck, für das zweiseitige Spektrum von x(t) . Begründen Sie
ihre Antwort mit einem Vergleich zwischen den Koeffizienten Ak, φk (Notation-II) und ck
(Notation-III).
Aufgabe 6 Chapter 3 FR : DFT und Chapter-5: Aliasing
[3+2+3=8 Punkte].
Der Matlab Code unten berechnet die DFT eines Signales.
clear all, close all, clc;
N = 50;?
Fs = 50e3;
% Fs= 50kHz
aux = 0:1:N-1;
t = (1/Fs)*aux;
f = (Fs/N)*aux;
fsig = [10e3 20e3];
y_t = 2*sin(2*pi*fsig(1)*t) + cos(2*pi*fsig(2)*t);
Y_f = (1/N)*fft(y_t);
stem(f,abs(Y_f)), …
6/10
Document1
SiSy, HS12, dqtm
Mit zwei verschiedenen N-Werten erzeugt man die folgenden Plots:
(a) Bestimmen Sie die Werte von N für die Variation-1 und für die Variation-2 des Plotes.
Begründen Sie ihre Antwort mit einem Vergleich zwischen jedem Plot und der
entsprechenden Frequenzauflösung.
Var-2:
Var-1:
(b) Würde in diesen beiden Plots das Spektrum des Signales durch den Aliasing Effekt
verfälscht? Bmk: Vergessen Sie nicht ihre Antwort zu begründen.
(c) Bestimmen Sie drei andere Werte für die harmonischen Frequenzen (fsig Vektor), welche
(wegen Aliasing) denselben Spektrum-Plot ergeben würden.
fsig(1)
fsig(0)
7/10
Document1
SiSy, HS12, dqtm
Aufgabe 7 Chapter 4 FT : Properties
[3+6=9 Punkte].
Das zweiseitige Amplitudenspektrum eines Tiefpassfilters GTPF(f) ist unten gegeben. Die
Bandbreite des Filters ist gleich fg = 1kHz .
¦GTPF(f)¦
1
-1k
1k
f [Hz]
(a) Sie wollen diesen Tiefpassfilter so modifizieren, dass der Filter doppel so schnell im
Zeitbereich reagiert (z.Bsp. die Impulsantwort des Filters doppel so schnell wird). Was
bedeutet das für die Bandbreite des Filters? Begründen Sie ihre Antwort mit einer Aussage
über die entsprechende Eigenschaft der Fouriertransformation.
(b) Jetzt modifizieren Sie das Filter nochmals, indem Sie die Impulsantwort des Filters g(t) mit
einem Cosinus cos(2πf0t) multiplizieren (mit f0=10kHz).
Welchen Typ von Filter bekommen Sie nun? Begründen Sie ihre Antwort mit einer Aussage
über die entsprechende Eigenschaft der Fouriertransformation und mit einer Skizze im
Frequenzbereich.
FT
Hinweis: Die Impulsantwort und der Frequenzgang sind eine FT-Paar
g t  
 G f 
8/10
Document1
SiSy, HS12, dqtm
Aufgabe 8 Chapter 5 AD-DA : DAC Reconstruction
[4+4=8 Punkte].
Der Plot eines diskreten Signal u[n] wird unten gegeben. Dieses Signal wird durch eine DAC,
mit einem ZOH (Zero-Order-Holder) und einem zusätzlichen Tiefpassfilter (Rekonstruktionsfilter
oder Anti-Imaging Filter) in ein kontinuierliches Signal gewandelt.
u[n]
ZOH
Ts = 2ms
u1(t)
Tiefpass
u2(t)
(a) Wie sehen die Signale u1(t) (nach der ZOH) und u2(t) (nach der Rekonstruktionsfilter) aus?
Vervollständigen Sie die Skizze unten und begründen Sie ihre Antwort mit einer kurzen
Aussage.
Bmk: Zeichnen Sie bitte u1(t) und u2(t) mit verschiedenen Farben, und identifizieren Sie
ihre Farbe in der Legende. Vergessen Sie nicht, die Zeit-Achse zu beschriften.
9/10
Document1
SiSy, HS12, dqtm
(b) Die Impulsantwort des ZOH gZOH(t) wird unten gegeben. Zeichnen Sie eine Skizze des
entsprechenden Amplitudenspektrums.
Hinweis: Vergleichen Sie die Impulsantwort mit dem Referenz Signal „square-pulse“.
¦gZOH(t)¦
1
Ts = 2 ms
Ts
10/10
t [s]
Document1