Analysis 8 Extremwertaufgaben
Werbung
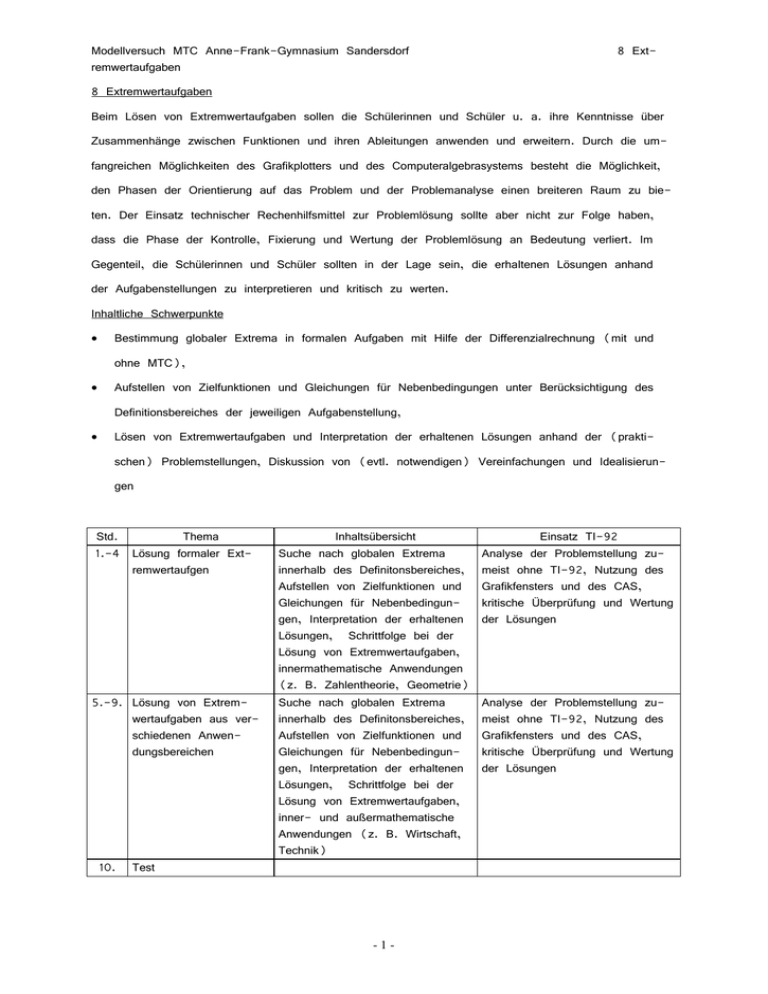
Modellversuch MTC Anne-Frank-Gymnasium Sandersdorf remwertaufgaben 8 Ext- 8 Extremwertaufgaben Beim Lösen von Extremwertaufgaben sollen die Schülerinnen und Schüler u. a. ihre Kenntnisse über Zusammenhänge zwischen Funktionen und ihren Ableitungen anwenden und erweitern. Durch die umfangreichen Möglichkeiten des Grafikplotters und des Computeralgebrasystems besteht die Möglichkeit, den Phasen der Orientierung auf das Problem und der Problemanalyse einen breiteren Raum zu bieten. Der Einsatz technischer Rechenhilfsmittel zur Problemlösung sollte aber nicht zur Folge haben, dass die Phase der Kontrolle, Fixierung und Wertung der Problemlösung an Bedeutung verliert. Im Gegenteil, die Schülerinnen und Schüler sollten in der Lage sein, die erhaltenen Lösungen anhand der Aufgabenstellungen zu interpretieren und kritisch zu werten. Inhaltliche Schwerpunkte Bestimmung globaler Extrema in formalen Aufgaben mit Hilfe der Differenzialrechnung (mit und ohne MTC), Aufstellen von Zielfunktionen und Gleichungen für Nebenbedingungen unter Berücksichtigung des Definitionsbereiches der jeweiligen Aufgabenstellung, Lösen von Extremwertaufgaben und Interpretation der erhaltenen Lösungen anhand der (praktischen) Problemstellungen, Diskussion von (evtl. notwendigen) Vereinfachungen und Idealisierungen Std. Thema 1.-4 Lösung formaler Extremwertaufgen 5.-9. Lösung von Extremwertaufgaben aus verschiedenen Anwendungsbereichen 10. Inhaltsübersicht Suche nach globalen Extrema innerhalb des Definitonsbereiches, Aufstellen von Zielfunktionen und Gleichungen für Nebenbedingungen, Interpretation der erhaltenen Lösungen, Schrittfolge bei der Lösung von Extremwertaufgaben, innermathematische Anwendungen (z. B. Zahlentheorie, Geometrie) Suche nach globalen Extrema innerhalb des Definitonsbereiches, Aufstellen von Zielfunktionen und Gleichungen für Nebenbedingungen, Interpretation der erhaltenen Lösungen, Schrittfolge bei der Lösung von Extremwertaufgaben, inner- und außermathematische Anwendungen (z. B. Wirtschaft, Technik) Test -1- Einsatz TI-92 Analyse der Problemstellung zumeist ohne TI-92, Nutzung des Grafikfensters und des CAS, kritische Überprüfung und Wertung der Lösungen Analyse der Problemstellung zumeist ohne TI-92, Nutzung des Grafikfensters und des CAS, kritische Überprüfung und Wertung der Lösungen Modellversuch MTC Anne-Frank-Gymnasium Sandersdorf remwertaufgaben -2- 8 Ext- Modellversuch MTC Anne-Frank-Gymnasium Sandersdorf remwertaufgaben 8 Ext- Lehrbücher für Aufgaben: [1] SCHMID, AUGUST; SCHWEIZER, WILHELM (Hrsg.): LS Mathematik Analysis Grundkurs Gesamtausgabe. 1. Auflage. Stuttgart: Ernst Klett Schulbuchverlag GmbH, 1992 [2] BOCK, HANS; WALSCH, WERNER (Hrsg.): Mathematik entdecken-verstehen-anwenden Analysis. 1. Auflage. München: R. Oldenbourg Verlag GmbH, 1993 [3] WEBER, KARLHEINZ; ZILLMER, WOLFGANG (Hrsg.): Mathematik Aufgabenbuch Analysis Analytische Geometrie Stochastik Sekundarstufe II. 1. Auflage. Berlin: paetec Gesellschaft für Bildung und Technik mbH, 1995 Aufgaben zum Abschnitt 5 Ableitungen 1. Aufgaben aus [1]: a) S. 128 Nr. 2 (Einführungsaufgabe) b) S. 130 Nr. 5-25 (Innermathematische Anwendungen) c) S. 132 Nr. 26-35 (Außermathematische Anwendungen) d) S. 138 Nr. 20-22 (Anwendungen aus der Wirtschaft) 2. Aufgaben aus [2]: a) S. 155 Nr. 23-25 (Einführungsaufgaben) b) S. 165 Nr. 29-30 (Innermathematische Anwendungen) c) S. 166 Nr. 31-36 (Außermathematische Anwendungen) 3. Aufgaben aus [3]: a) S. 56 Nr. DA 122-DA 128 (Außermathematische Anwendungen) b) S. 57 Nr. DA 129-DA 134 (Innermathematische Anwendungen) 4. In einer Mühle (Punkt M) brennt es. Die Feuerwehr fährt vom Spritzenhaus (Punkt H) querfeldein zum Bach, um Löschwasser zu tanken, dann zur Mühle. An welchem Punkt B muß sie den Bach treffen, um möglichst auf kürzestem Wege bei der Mühle einzutreffen (Skizze). M H B 5. Welches unter allen Rechtecken mit gegebener Diagonalenlänge hat den größten Flächeninhalt (Umfang)? 6. Welches von allen gleichschenkligen Dreiecken, die man einen Kreis mit gegebenen Radius einbeschreiben kann, besitzt maximalen Flächeninhalt? 7. Rindfleisch enthält 6% Fett und 20% Eiweiß, Haselnüsse 30% Fett und 10% Eiweiß. Der Mindestbedarf eines Menschen pro Tag ist 60g Fett und 80g Eiweiß. Ein Kilogramm Rindfleisch kos-3- Modellversuch MTC Anne-Frank-Gymnasium Sandersdorf remwertaufgaben tet kann der 8 Ext- 11,99 DM und ein Kilogramm Haselnüsse 9,99 DM. Für welchen kleinsten Geldbetrag tägliche Mindestbedarf beschafft werden? 8. Beim Bau von Wechselstromtransformatoren ist es von Wichtigkeit, das Innere einer Spule von kreisförmigen Querschnitt durch einen Eisenkern von kreuzförmigen Querschnitt möglichst auszufüllen. Wie sind die Abmessungen des Eisenkerns zu wählen, wenn der Spulenradius 8cm beträgt (Skizze)? 9. Eine Querfeldeinstrecke habe den Startpunkt S und den Zielpunkt Z, die auf verschiedenen Seiten eines Weges w liegen. Südlich des Weges (dort liegt S) verläuft die Strecke über einen morastigen Acker, auf dem ein Läufer mit einer Durchschnittsgeschwindigkeit von 12 km/h vorankommt. Nördlich des Weges (dort liegt Z) liegt eine Wiese, auf welcher der Läufer in 20 Minuten 5 km zurücklegt. An welcher Stelle muß der Läufer den Weg w kreuzen, damit er die Strecke von S nach Z in möglichst kurzer Zeit zurücklegt? 10. Ein Mathematiker bestimmt in seinem Testament, dass auf seinem Grab ein rechteckiger Stein mit aufgesetztem Halbkreis stehen soll. Dieser solle so hergestellt werden, dass bei festem Gesamtumfang von 10m der Flächeninhalt der Vorderseite möglichst groß ist. 11. Ein unausgebauter Dachboden hat als Querschnitt ein gleichschenkliges Dreieck von 8m Breite und 5m Höhe. Die Haubesitzer wollen auf dem Dachboden ein Zimmer mit rechteckigem Querschnitt bauen. Sie berechnen die Höhe mit 2,5m und die Breite mit 4m und denken, damit den optimalen Querschnitt gefunden zu haben. Stimmt das? -4- Modellversuch MTC Anne-Frank-Gymnasium Sandersdorf remwertaufgaben 8 Ext- Arbeitsblatt 1. Geben Sie zu den folgenden Funktionen f in den angegebenen Intervallen I jeweils die Koordinaten von lokalen und globalen Extrempunkten an. Funktionsgleichung Intervall I Lokale(r) Extrempunkt(e) (-2;4) f(x) = 2x – 3 [-2;4] f(x) = -5- Globale(r) Extrempunkt(e)