Konvexe Funktionen

Proseminar Mathematisches Problemlösen
Thema: Konvexe Funktionen
Definition: Sei K Teilmenge des Rⁿ eine konvexe Menge
a) Eine Funktion f: K → R heißt konvex(streng konvex), falls
f(t x + (1-t)y) ≤ t f(x) + (1-t) f(y),
(<)
x,y є K und t є [0,1]
b) Eine Funktion f: K → R heißt konkav(streng konkav), falls
f(t x + (1-t)y) ≥ t f(x) + (1-t) f(y),
(>)
x,y є K und t є [0,1]
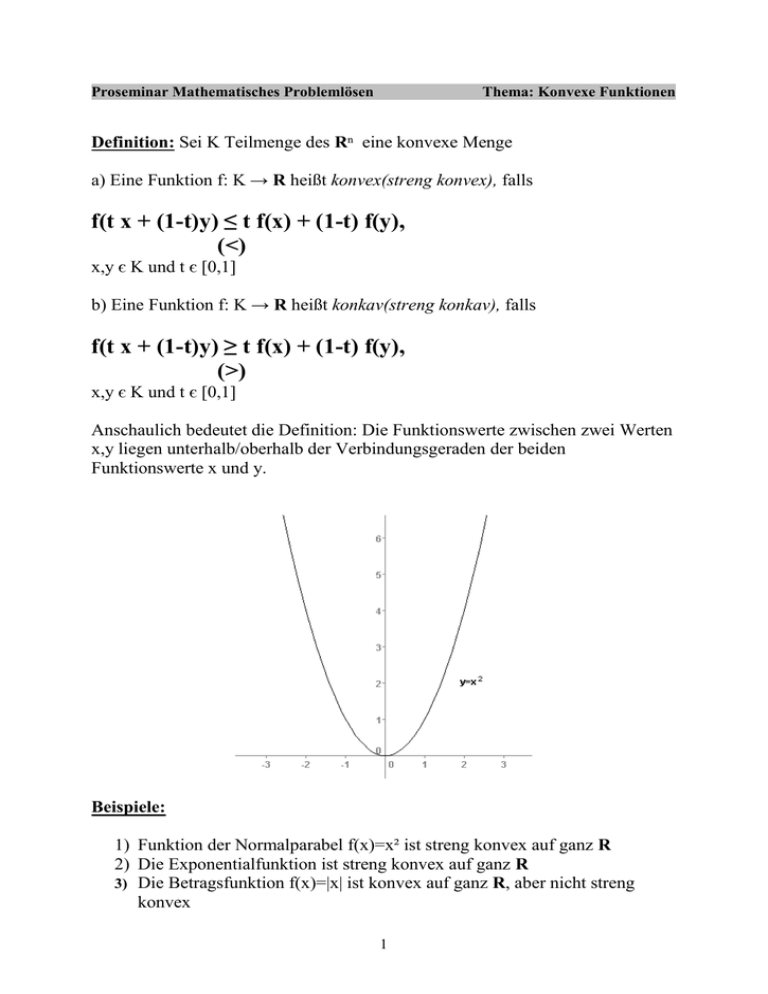
Anschaulich bedeutet die Definition: Die Funktionswerte zwischen zwei Werten
x,y liegen unterhalb/oberhalb der Verbindungsgeraden der beiden
Funktionswerte x und y.
Beispiele:
1) Funktion der Normalparabel f(x)=x² ist streng konvex auf ganz R
2) Die Exponentialfunktion ist streng konvex auf ganz R
3) Die Betragsfunktion f(x)=|x| ist konvex auf ganz R, aber nicht streng
konvex
1
Proseminar Mathematisches Problemlösen
Thema: Konvexe Funktionen
Die besondere Bedeutung konvexer bzw. konkaver Funktionen liegt darin, dass
sie allgemeiner als lineare Funktionen sind, aber einfach zu untersuchende
Eigenschaften haben, die viele Aussagen über nichtlineare Systeme,
insbesondere über nichtlineare Optimierungsprobleme ermöglichen.
Eigenschaften:
- Der Graph einer konvexen Funktion ist so gewölbt, dass die Menge der
Punkte oberhalb des Graphen, der so genannte Epigraph, eine konvexe
Menge ist.
- Der Graph einer konkaven Funktion ist so gewölbt, dass die Menge der
Punkte unterhalb des Graphen eine konvexe Menge ist.
- Zu beachten ist, dass eine nicht-konvexe Funktion nicht automatisch
konkav sein muss, d.h. konvex und konkav sind hier nicht das exakte
Gegenteil voneinander.
- Eine Funktion f ist genau dann konvex (konkav), wenn die Funktion –f
konkav (konvex) ist.
- Für eine monoton steigende und konvexe (konkave) Funktion ist die
Umkehrfunktion konkav (konvex).
- Jede lineare Funktion ist konvex und konkav.
- Die Sinus-, Cosinus- und Tangensfunktion sind weder konvex noch
konkav.
- Sind f und g zwei konvexe (konkave) Funktionen, so ist auch jede
Linearkombination af+bg mit a,b є R+ wieder konvex (konkav).
- Für stetige Funktionen gibt es einen schwächeren Konvexitätsbegriff.
Aufgaben:
1) Sei K Teilmenge des Rⁿ eine konvexe Menge und f: K → R eine
konvexe Funktion. Beweisen Sie, dass die Menge F Teilmenge von K x R
F={(x,t) є K x R : f(x) ≤ t} (Punkte oberhalb des Graphen von f) konvex
ist.
Lösung:
Seien y1=(x1,t1) und y2=(x2,t2) aus F, d.h. t1 ≥ f(x1), t2 ≥f(x2). Dann ist
f(α1 x1+α2 x2) ≤ α1f(x1)+ α2 f(x2) ≤ α1 t1 + α2 t2.
Das ist aber zu der Konvexitätsbedingung
α1 y1 + α2 y2 = (α1 x1+α2 x2, α1 t1+α2 t2 ) є F
äquivalent.
2
Proseminar Mathematisches Problemlösen
Thema: Konvexe Funktionen
2) Seien K Teilmenge des Rⁿ eine konvexe Menge, g: K → R eine konvexe
Funktion und c є R eine Konstante.
a) Beweisen Sie, dass die Menge Kc = {x є K : g(x) ≤ c} konvex ist.
Lösung:
Seien x,y є Kc. Dann ist g(t x +(1-t)y) ≤ t g(x)+(t-1)g(y) ≤ t c+(1-t)c=c. Daher
ist t x+(1-t)y є Kc.
b) Ist die Umkehrung auch richtig: Folgt aus der Konvexität von Kc für alle
c, dass g konvex ist?
Lösung:
Nein, die Umkehrung gilt i.A. nicht. Man nehme z.B. eine beliebige monoton
steigende Funktion. Dann ist Kc=(-∞, g^(-1)(c)] konvex. Die Funktion muss
aber nicht konvex sein, vgl. beispielsweise g(x) = x³.
3) Sei K Teilmenge des Rⁿ konvex. Beweisen Sie: eine stetige Funktion f: K
→ R ist genau dann konvex, wenn für alle x,y є K gilt
f ((x+y)/2) ≤ (f(x)+f(y))/2. (☼)
Bemerkung: In anderen Worten, die Konvexitätsbedingung kann für stetige
Funktionen durch diese schwächere Bedingung ersetzt werden.
Lösung:
In eine Richtung ist die Behauptung offensichtlich: ist f konvex, so gilt die
Relation
insbesondere für t=½.
Sei nun (☼) erfüllt. Halten wir zwei Punkte x1,x2 є K mit x1 ≠ x2 fest. Wir
bezeichnen mit D die Strecke D=[x1,x2] = {(1-t)x1+t x2 : t є [0,1]}.
Die Funktion g(t) = f((1-t)x1+t x2) (Einschränkung von f auf D, parametrisiert
durch t) erfüllt ebenfalls (☼) bezüglich t. Jede lineare Funktion g1(t) = at+b
ist konvex, erfüllt also ebenfalls (☼). Betrachten wir die Hilfsfunktion
h: [0,1] → R gegeben durch h = g-g1 mit
g1(t) = (1-t)f(x1)+t f(x2) = (1-t)g(0)+t g(1).
Wie leicht einzusehen ist, gilt g1(0)=g(0) und g1(1)=g(1). Die Differenz h
erfüllt folglich sowohl die Randbedingungen h(0)=h(1)=0, als auch die
Konvexitätsbedingung (☼), d.h.
h((t1+t2)/2) ≤ (h(t1)+h(t2))/2 für alle t1,t2 є [0,1].
Aus h(0)=h(1)=0 folgt somit h(½) ≤ 0. Ferner gilt
h(¼) ≤ ½(h(0)+h(½)) ≤ 0 und h(¾) ≤ ½(h(½)+h(1)) ≤ 0 u.s.w.
3
Proseminar Mathematisches Problemlösen
Thema: Konvexe Funktionen
Für jeden Punkt der Form tn,m = n2^(-m), n,m є N gilt h(tn,m) ≤ 0. Da aber die
Punkte { tn,m : n,m є N, n < 2^m} überall dicht in (0,1) liegen, gilt für jedes t
є (0,1) die Abschätzung h(t) ≤ 0. Ausgeschrieben bedeutet das
f((1-t)x1+t x2)-[(1-t)f(x1)+t f(x2)] ≤ 0,
was zu der Konvexitätsbedingung
f((1-t)x1+t x2) ≤ (1-t)f(x1)+t f(x2)
äquivalent ist.
4) Sei f eine auf dem Intervall [a,b] monoton steigende konvexe Funktion.
Zeigen sie, dass die inverse Funktion g = f^(-1) auf dem Intervall
[g(a),g(b)] konkav ist.
Lösung:
Zu zeigen ist g(t y1+(1-t)y2) ≥ t g(y1)+(1-t)g(y2) für alle y1, y2 є [g(a),g(b)] und
t є [0,1]. Sei yj = f(xj) , j=1,2. Dann ist
t g(y1)+(1-t)g(y2) = tx1 + tx2 bzw.
g(t y1+(1-t) y2) = g(t f(x1)+(1-t)f(x2)) ≥ g(f(t x1+(1-t)x2)) = t x1+(1-t)x2.
Die mittlere Ungleichung folgt aus der Konvexität von f, d.h. aus
t f(x1)+(1-t)f(x2) ≥ f(t x1 + (1-t)x2), und aus der Monotonie von g.
5) Zeigen sie, dass die Exponentialfunktion auf R konvex und entsprechend
ln y auf y > 0 konkav ist.
Lösung:
Da die Exponentialfunktion stetig ist, reich es nach der Aufgabe 3 zu zeigen:
e^((x+y)/2) ≤ ½ (e^x + e^y)
Dies folgt aber aus der AM-GM-Ungleichung:
e^((x+y)/2) = (e^(x+y))^ ½ = (e^x * e^y)^½ ≤ ½(e^x+e^y).
Die zweite Behauptung (ln y konkav) folgt aus der Konvexität der
Exponentialfunktion (siehe Aufgabe 4).
6) Sei K Teilmenge des Rⁿ eine konvexe Menge und f: K → R eine
Funktion. Beweisen Sie: Die Funktion f ist genau dann konvex, wenn für
jede Gerade g Teilmenge des Rⁿ die Einschränkung f|g von f auf g ∩ K
(falls die Schnittmenge nichtleer ist) konvex ist.
Lösung:
„“: Sei f: K → R konvex und sei der Schnitt g ∩ K nicht leer. Betrachten
wir zwei Punkte x1, x2 є g ∩ K. Dann ist die ganze gerade Strecke [x1, x2],
siehe Def. Konvexe Mengen, in g ∩ K enthalten wegen
(☼) [x1, x2] Teilmenge von g und [x1, x2] Teilmenge von K (da K konvex).
4
Proseminar Mathematisches Problemlösen
Thema: Konvexe Funktionen
Aus der Konvexität von f auf K folgt nun f(t x1+ (1-t) x2) ≤ t f(x1) + (1-t)f(x2),
d.h. die Funktion f ist auf g ∩ K konvex.
„“: Sei nun die Einschränkung f|g von f auf jede Gerade konvex.
Betrachten wir zwei Punkte x1, x2 є K und die Gerade g=(x1, x2), die durch
diese beiden Punkte geht. Die gerade Strecke [x1, x2] ist in g ∩ K enthalten
wegen (☼). Aus der Konvexität von f auf g ∩ K folgt nun f(t x1+ (1-t) x2) ≤ t
f(x1) + (1-t) f(x2). Da dies für zwei beliebige Punkte in K gilt, ist f auf K
konvex.
Quellen:
-
Harro Heuser, Lehrbuch der Analysis Teil 1
Konrad Königsberger, Analysis 1
Skript zur Vorlesung Optimierungstheorie im SS 2005 von Prof. Dr. Andreas Kirsch
Unterlagen von Dr. Natalia Grinberg
www.wikipedia.org
© Anne Tremmel
5