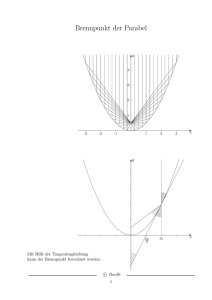
Aufgaben1

Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
3 C, D Parabel interpretieren
y = ax² + bx + c ist die allgemeine Gleichung einer Parabel.
a) Geben Sie ein konkretes Beispiel an, das eine nach unten offene Parabel beschreibt, die ihren
Scheitel auf der y-Achse hat (siehe Abbildung). Erklären Sie, welche Bedingung die Koeffizienten
a,b,c für diesen Fall aufweisen müssen.
b) Argumentieren Sie, ob eine nach unten offene Parabel mit Scheitel auf der y-Achse immer
Nullstellen aufweisen muss.
Lösung:
a) Interpretieren, argumentieren: z:B. a = -2, b = 0, c = 3  y = -2x² + 3
Eine nach unten offene Parabel hat den Koeffizienten a negativ. Wenn der Scheitel auf der yAchse liegt, dann muss b = 0 sein und c gibt die Schnittstelle der Parabel auf der y-Achse an.
b) Argumentieren: Es gibt drei mögliche Fälle:
Wenn c > 0, dann gibt es im Falle einer nach unten offenen Parabel 2 reelle Nullstellen
Wenn c = 0, dann schneidet die y-Achse die Parabel nicht, sondern berührt sie: Es gibt eine
Nullstelle, den Koordinatenursprung.
Wenn c < 0, dann gibt es keine Nullstellen (Lösungen der Gleichung sind imaginär). Die Parabel
liegt mit ihrem Scheitel unterhalb der x-Achse.
1
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
3C,D Parabel auswählen
Welche der folgenden Abbildungen entspricht der Funktion f(x), wenn
f(x) = ax² + bx + c und a>0 und c<0. Begründen Sie Ihren Lösungsvorschlag.
Abb.1
Abb. 2
Abb. 3
Abb. 4
Lösung: Interpretieren und argumentieren
Abb. 1, da bei a >0 der Graph der Funktion nach oben geöffnet ist und wenn c< 0 ist, dann bedeutet
dies, dass die die y-Achse im negativen Bereich von der Parabel geschnitten wird.
2
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
3A,C Anhalteweg: Modellieren und Transferieren mit funktionalen Zusammenhängen
Die Fahrschulregel für den Anhalteweg bei Kraftfahrzeugen lautet:
Anhalteweg in m = Bremsweg + Reaktionsweg
Bremsweg in m = Geschwindigkeit des PKW in km/h durch 10 dividieren und
das Resultat quadrieren
Reaktionsweg in m = Geschwindigkeit in km/h mal 3 durch 10
Finden Sie ein Modell, wie Sie den Bremsweg, den Reaktionsweg und den Anhalteweg gemäß der
Fahrschulregeln als Funktion der Fahrzeuggeschwindigkeit darstellen können.
Lösung: Interpretieren und Dokumentieren
Tabellarisch:
Geschwindigkeit v in km/h 0 20 40 60
Bremsweg sb in m
0 4 16 36
Reaktionsweg sr in m
0 6 12 18
Anhalteweg sa in m
0 10 28 54
80 100 120 140
64 100 144 196
24 30 36 42
88 130 180 238
Als Funktionsgleichung:
Grafische Darstellung:
3
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
3B, C, D Benzinverbrauch 1
Der Kraftstoffverbrauch eines PKW ist in guter Näherung eine quadratische Funktion der
Fahrgeschwindigkeit. Für einen Klein-PKW einer bestimmten Automarke gibt die folgende Formel
den Zusammenhang zwischen dem Benzinverbrauch y (in Liter je 100 km) und der Geschwindigkeit v
(zwischen 50 km/h und 140 km/h) an:
.
a) Berechnen Sie den Benzinverbrauch bei einer Geschwindigkeit von 130 km/h.
b) Bei welcher Geschwindigkeit wird gegenüber a) eine 20-prozentige Verringerung des
Benzinverbrauchs erreicht?
c) Welche Bedeutung könnte die Einschränkung des Geschwindigkeitsbereichs für den
Benzinverbrauch haben?
d) Welche weitere Annahme ist in der Formulierung der Angabe stillschweigend getroffen worden?
Lösung:
a) Für v in der Formel 130 einsetzen und berechnen. y = 9,231 l/100km
b) 80 % des Ergebnisses von a) berechnen und für y in die Formel einsetzen und die Gleichung
lösen. v = 110,31 km/h. 2.Lösung ist auszuschließen, weil sie negativ ist ( -28,96)
c) Mögliche Antworten: Eine höhere Geschwindigkeit als 130 km/h ist auf Österreichs Straßen nicht
erlaubt
Die grafische Darstellung dieses Modells zeigt bei v = 0 den Benzinverbrauch im Stehen bei
laufendem Motor von 5,5l/100km. Beim Stehen mehr Benzin zu verbrauchen als beim Anfahren
ist nicht wahrscheinlich. (Modell hier nicht passend)
Die Geschwindigkeit liegt bei diesem Modell mit dem minimalen Verbrauch liegt bei 40,68 km/h
und beträgt 4,5 Liter/100 km.
d) Konstante Geschwindigkeit über die gesamten 100 Kilometer.
4
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
3A,B,C,D Benzinverbrauch 2
Laut Messungen eines Autofahrerclubs ergibt sich für eine bestimmte Automarke abhängig von der
Geschwindigkeit v (in km/h) folgender Benzinverbrauch BV (in Liter / 100 km):
v
BV
30
40
6,25 6,2
80
7,0
Man geht davon aus, dass der Benzinverbrauch quadratisch von der Geschwindigkeit abhängt.
a) Wie lautet der Funktionsterm für den Benzinverbrauch?
b) Wie hoch ist der Benzinverbrauch bei einer Durchschnittsgeschwindigkeit von 120 km/h?
c) Berechnen Sie bei welcher Geschwindigkeit der Verbrauch genau 8 Liter/100 km beträgt und
interpretieren Sie das Ergebnis.
Erklären Sie, wie man diese Aufgabe auch grafisch lösen kann.
d) Wie viele Lösungen gibt es in Aufgabe c? Welche anderen Lösungsfälle können bei quadratischen
Gleichungen (in R) noch auftreten? Begründen Sie mit Hilfe der Lösungsformel!
Lösung :
a) Modellieren, Technologieeinsatz Ansatz: BV(v) = av² + bv + c
I. 6,25 = 900a + 30b + c
II. 6,2 = 1600a + 40b + c
III. 7,0 = 6400a + 80b + c
BV(v) = 0,0005v² - 0,04v + 7
b) Operieren: BV(120) = 0,0005.120² - 0,04.120 + 7 = 9,4 Liter pro 100 km/h
c) Operieren ohne und mit Technologie: BV(v) = 8
8 = 0,0005v² - 0,04v + 7
0 = 0,0005v² - 0,04v -1
v1 = -20 km/h
v2 = 100 km/h
Antwort: Bei 100 km/h beträgt der Verbrauch 8 Liter/100 km. Die negative Lösung ist nicht
sinnvoll. Sie ergibt sich aufgrund der Symmetrie der quadratischen Funktion, liegt aber nicht im
Definitionsbereich dieser Funktion.
grafische Lösung:
Zeichnung der beiden Funktionen BV(v) = 0,0005v² - 0,04v + 7 und BV = 8
Lösung ist der Schnittpunkt (im pos. Geschwindigkeitsbereich)
d) Argumentieren: die Parabel hat 2 Nullstellen, die Lösungsformel führt zu 2 reellen Lösungen. (Die
Diskriminante ist positiv, daher ist der Wert der Wurzel eine reelle Zahl)
Allgemeine Lösungsfälle sind abhängig vom Wert der Diskriminanten bzw. vom Ergebnis der
Wurzel in der Lösungsformel. Ist der Wert der Wurzel imaginär, dann gibt es keine reellen
Lösungen. Ist der Wert der Wurzel in der Lösungsformel = 0,
dann gibt es nur eine Lösung –b / (2a)
5
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
2 A, B, C Brückenbogen:
Der Brückenbogen dieser Brücke hat die Form einer Parabel.
a) Ermitteln Sie die Gleichung der Parabel, indem Sie den Ursprung (0/0) in den Scheitel des
Brückenbogens legen.
b) Kann ein Frachtschiff die Fahrrinne am Rande noch gefahrlos durchfahren, wenn es 17m über die
Wasseroberfläche ragt?
Lösung:
a) Modellieren, Operieren
A(-40/-20)
-20 = 1600a - 40b
B(40/20)
-20 = 1600a + 40b
0 (0/0)  c=0

y = - 0,0125x²
b) Operieren, Interpretieren: P(25/y) y = - 0,0125  625 = -7,81m
24m – 7,81m =16,19 m Fahrhöhe stehen zur Verfügung. Antwort: nein!!
3 A,B,C, D Stahlbrücke
Die Stützpfeiler einer Stahlbrücke haben auf Parabelbögen
zusätzliche Streben, die im Abstand von einem Meter zueinander
angeordnet sind (siehe Skizze)
a) Ermitteln Sie die Funktionsgleichung der in der Zeichnung
dargestellten Parabel und erläutern Sie den Lösungsweg.
b) Berechnen Sie die Längen der verschiedenen Streben im
ersten Bogen.
c) Erörtern Sie die Lösungsfälle einer quadratischen Gleichung und ihre graphische Interpretation!
Erwartung:
a) Modellieren, Operieren
Möglicher Lösungsweg:
Betrachte nur den ersten Bogen: 3 Punkte bekannt (0/6), S(4/10), (8/6)
y = ax² + bx + c
3 Variablen, daher 3 Gleichungen nötig:
I. f(0)=6
c=6
II. f(4) = 10
 10 = 16a + 4b + 6
III. f(8) = 6
 6 = 64a + 8b + 6
mit oder ohne Technologieeinsatz: a = -0,25; b = 2; c = 6
y = -0,25x² + 2x + 6
6
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
b) Operieren, Interpretieren
Wertetabelle:
x
0
1
s(x) in m
4
2,25
2
1
3
0,25
4
0
c) Argumentieren, Interpretieren:
Allgemeine Lösungsfälle sind abhängig vom Wert der Diskriminanten bzw. vom Ergebnis der
Wurzel in der Lösungsformel.
Ist der Wert der Wurzel imaginär (Diskriminante negativ), dann gibt es keine reellen Lösungen –
die Parabel schneidet die x-Achse nicht, sie hat keine Nullstellen.
Ist der Wert der Wurzel in der Lösungsformel = 0 (Diskriminante = 0), dann gibt es nur eine
Lösung –b / (2a), die Parabel berührt die x-Achse. Die Parabel hat eine Nullstelle.
Ist der Wert der Wurzel reell (positive Diskriminante) dann führt die Lösungsformel zu 2 reellen
Lösungen. Die Parabel schneidet die x-Achse 2-mal, sie hat 2 Nullstellen.
3 A,B,C Parabelkirche
Die Parabelkirche in Gelsenkirchen hat eine Vielzahl von parabelförmigen Bögen.
a) Beschreiben Sie die folgenden Eigenschaften der eingezeichneten Parabel:
Definitionsbereich, Monotonie, Nullstellen, höchster Punkt.
b) Durch welche Funktionsgleichung lässt sich im angegebenen Koordinatensystem die
eingezeichnete Parabel am besten beschreiben?
Lösung:
a) Interpretieren:
Definitionsmenge: -2≤ x ≤ 2
Nullstellen N1(-2|0), N2(2|0)
Hochpunkt (0|5)
monoton steigend von -2≤ x ≤ 0
monoton fallend von 0≤ x ≤ 2
b) Modellieren und Operieren
Es handelt sich um eine quadratische Funktion mit dem Scheitel in 0|5 -b/ 2a = 0, daher b = 0,
also eine rein quadratische Funktion. ax² + c = 0
0| 5 auf der Parabel: a . 0 + c = 5  c = 5
2 | 0 auf der Parabel: a  4 + c = 0  a = -5/4
Gleichung: y = - 1,25 x² + 5
7