Aufgaben2

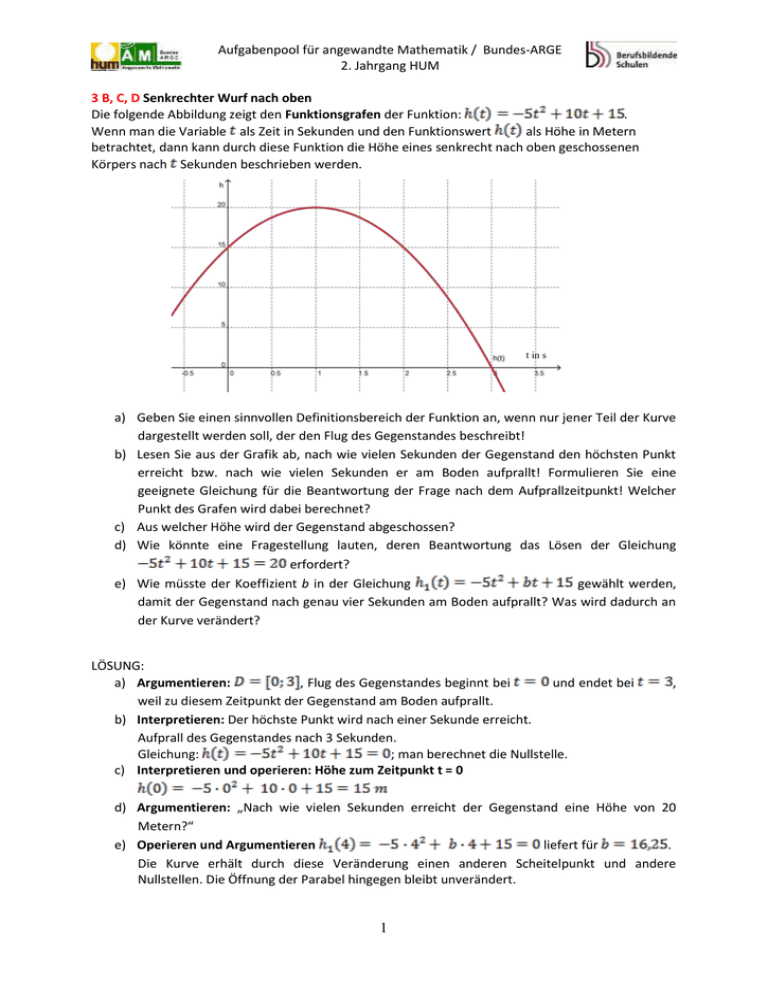
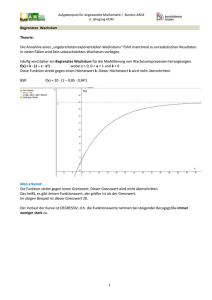
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
3 B, C, D Senkrechter Wurf nach oben
Die folgende Abbildung zeigt den Funktionsgrafen der Funktion:
.
Wenn man die Variable als Zeit in Sekunden und den Funktionswert
als Höhe in Metern
betrachtet, dann kann durch diese Funktion die Höhe eines senkrecht nach oben geschossenen
Körpers nach Sekunden beschrieben werden.
t in s
a) Geben Sie einen sinnvollen Definitionsbereich der Funktion an, wenn nur jener Teil der Kurve
dargestellt werden soll, der den Flug des Gegenstandes beschreibt!
b) Lesen Sie aus der Grafik ab, nach wie vielen Sekunden der Gegenstand den höchsten Punkt
erreicht bzw. nach wie vielen Sekunden er am Boden aufprallt! Formulieren Sie eine
geeignete Gleichung für die Beantwortung der Frage nach dem Aufprallzeitpunkt! Welcher
Punkt des Grafen wird dabei berechnet?
c) Aus welcher Höhe wird der Gegenstand abgeschossen?
d) Wie könnte eine Fragestellung lauten, deren Beantwortung das Lösen der Gleichung
erfordert?
e) Wie müsste der Koeffizient b in der Gleichung
gewählt werden,
damit der Gegenstand nach genau vier Sekunden am Boden aufprallt? Was wird dadurch an
der Kurve verändert?
LÖSUNG:
a) Argumentieren:
, Flug des Gegenstandes beginnt bei
und endet bei
weil zu diesem Zeitpunkt der Gegenstand am Boden aufprallt.
b) Interpretieren: Der höchste Punkt wird nach einer Sekunde erreicht.
Aufprall des Gegenstandes nach 3 Sekunden.
Gleichung:
; man berechnet die Nullstelle.
c) Interpretieren und operieren: Höhe zum Zeitpunkt t = 0
,
d) Argumentieren: „Nach wie vielen Sekunden erreicht der Gegenstand eine Höhe von 20
Metern?“
e) Operieren und Argumentieren
liefert für
.
Die Kurve erhält durch diese Veränderung einen anderen Scheitelpunkt und andere
Nullstellen. Die Öffnung der Parabel hingegen bleibt unverändert.
1
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
3 A,B,C Silvesterrakete
Die Flugbahn einer Silvesterrakete verläuft parabelförmig (siehe
Skizze).
a) Wie beschreibt man eine quadratische Funktion?
Was sagen die dabei auftretenden Kennzahlen aus?
b) Ermitteln Sie die Funktionsgleichung der in der Zeichnung
dargestellten Wurfparabel und erläutern Sie den Lösungsweg.
c) Berechnen Sie die horizontale Entfernung der Auftreffstelle von
der Abschussstelle.
Erwartung:
a) Interpretieren:
Die quadratische Funktion wird allgemein angesetzt mit: y = ax² + bx + c.
Die Koeffizienten a, b und c bestimmen den Wertebereich und die Form des Graphen.
a > 0: der Graph ist nach oben geöffnet.
a < 0: der Graph ist nach unten geöffnet.
Je kleiner der Betrag von a ist, desto schmaler wirkt der Graph.
Eine Veränderung des Parameters c bewirkt eine Verschiebung in y-Richtung.
Wird c um eins erhöht, dann wird der Graph um eine Einheit nach oben verschoben. Wird c um eins verringert, wird der Graph
dagegen um eine Einheit nach unten verschoben.
Schwieriger deutbar ist der Parameter b. Eine Veränderung von b bewirkt eine Verschiebung der
Parabel sowohl in x- als auch in y-Richtung. Zumindest die Lage des Parabelscheitels kann
aufgrund des Vorzeichens von b abgelesen werden: Ist b > 0, dann liegt der Scheitel links und hat
eine negative x- Koordinate, ist b < 0, so liegt der Scheitel rechts und hat eine positive xKoordinate. (Die Lage des Scheitels erhält man mit: x = -b/2a und y = c – b²/4a)
Annahme: y = 2x² + 4x -12
a = 2: nach oben offene Parabel, enger wirkend als die Normparabel y = x²
c = -12: Die Parabel schneidet die y-Achse bei -12
b = 4 … Der Scheitel der Parabel liegt links im Koordinatensystem (x=-1, y =-14)
( Erhöht man b um 1, dann verschiebt sich die Parabel nach links um 1 / 2a und nach unten um (2b+1)/4a Einheiten. Vermindert man
um 1, dann ist eine Verschiebung um 1/2a nach rechts und 2b-1)/4a nach oben)
b) Modellieren, Operieren, Dokumentieren
Möglicher Lösungsweg:
y = ax² + bx + c
3 Variablen, daher 3 Gleichungen nötig:
I. f(0)=0
c=0
II. f(8) = 32
 32 = 64a + 8b
III. f(16) = 0
 0 = 256a + 16b
mit oder ohne Technologieeinsatz: a = -0,5; b = 8
 y = - 0,5x² + 8x
c) Interpretieren, Operieren
y = (-40) in Funktionsgleichung einsetzen: -40 = - 0,5x² + 8x
quadrat. Gleichung lösen: 0,5x² - 8x - 40 = 0  Lösungen: 20 (und -4 D)
Entfernung 20 m
2
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
3 A,B,C,D Tennisball
Die Wurfhöhe eines Tennisballes kann näherungsweise durch die Funktion:
s(x) = s0 - 4,9 x²/v² beschrieben werden, wobei x die waagrechte Entfernung von der
Abwurfstelle in Meter bedeutet, v die Abschlaggeschwindigkeit des Balls ist und s0 die
Abschlaghöhe = Schulterhöhe des Spielers + Unterarmlänge + Tennisschläger. Sie wird
angenommen mit s0 ≈ 200 cm.
Zusatzinformationen:
Länge Tennisplatz: 23,77 m, Netzhöhe: 0,914 m
a) Stellen Sie die Flugbahn des Balles bei waagrechter Abschlagrichtung bei mindestens 3
unterschiedlichen Abschussgeschwindigkeiten in einem gemeinsamen Koordinatensystem grafisch dar und interpretieren Sie das Ergebnis. (Bei Lösung mit GTR genügt eine
Skizze).
b) Wie groß muss die Abschlaggeschwindigkeit v(t=0) des Tennisballes sein, damit der Ball
gerade noch über das Netz geht? Geben Sie das Ergebnis in km/h an.
c) Die Geschwindigkeit v beim Abschuss v = 25,3 m/s. Trifft der Spieler ins gegnerische
Feld? Wie weit vom Netz entfernt schlägt der Ball auf?
d) Was kann der Spieler beim Abschlag verändern, wenn er bei kleinerer
Abschlaggeschwindigkeit den Ball doch noch über das Netz schlagen will?
Lösungen: a) Technologieeinsatz (hier mit Geogebra und Schieberegler)
Die Abschussgeschwindigkeit legt die Flugweite fest. Je größer die Geschwindigkeit,
desto weiter fliegt der Ball. Bei 40 m/s fliegt er bereits über den Platz hinaus.
3
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
b) Operieren: Die Netzkoordinate, halbe Spielfeld-Weite und Höhe ist (11,885 | 0,914)
Gleichung nach v auflösen
(zB mit Technologie)
0,914 = 2 – 4,911,885²/v² 
v = 25,25 m/s = ca. 91 km/h
c) Operieren: Gleichung nach x auflösen
0= 2 – 4,9 x²/25,3²
x= 16,16 m
Der Ball trifft etwas über 4 m hinter dem Netz auf, Flugweite 16,16 m.
d)Argumentieren:
Um Höhe zu gewinnen müsste der Spieler den Abschlag nicht waagrecht machen,
sondern den Ball schräg nach oben nach Art eines schrägen Wurfs schlagen.
4
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
3 A, B,C,D Kormoran
Der Kormoran ist ein Vogel, der sich in den Donauauen von Fischen
ernährt. Sein 6 Sekunden langer Beuteflug entspricht der Kurve
h(t)= t² - 8t + 15; h in Meter (m), t in Sekunden (s).
Die t-Achse (Abszisse) entspricht der Wasseroberfläche.
a) Beschreiben Sie, was in der 3. Sekunde passiert!
b) Berechnen Sie, wann der Kormoran – vielleicht mit einem Fisch –
wieder auftaucht?
c) Skizzieren Sie die Flugbahn!
d) In welcher Höhe startet der Beuteflug?
e) Verändern Sie die Funktionsgleichung so, dass beschrieben wird, wie ein Vogel bei gleichem
Startpunkt genau an der Stelle seines vorherigen tiefsten Eintauchpunktes nun auf der
Wasseroberfläche nach dem Fisch greift! (Lösen mit Kenntnissen des 2. JG.)
Lösung:
a) Operieren, Interpretieren
h(3) =3² - 8  3+15
h(3) = 0
Der Kormoran taucht ins Wasser ein.
b) Operieren, interpretieren
Berechnung der Nullstellen, Interpretieren der 2. NSt als Auftauchen, Technologieeinsatz
möglich.
h(t) = t² - 8t + 15 = 0
t1 = 3sec
t2 = 5sec
c) Operieren
d) Interpretieren
h(0) = 15 m
e) Modellieren, Operieren und Argumentieren
Der Scheitel verschiebt sich nach oben, die Flugbahn wird etwas flacher. Die tiefste Stelle =
Scheitel des Flugs befindet sich bei (4|0)
Auf der neuen Bahn kennt man die Bedingungen Startpunkt (0|15), tiefste Stelle (4|0). Der
tiefste Punkt ist die eine Nullstelle der Funktion, daher gilt: - b/2a = 4
Gleichungssystem: 15 = c, 0 = 16 a + 4b + 15, und - b = 8a  (mit oder ohne Technologie)
hneu(t)= 0.9375 t² -7,5t + 15
5
Aufgabenpool für angewandte Mathematik / 2. Jahrgang
Bundes-ARGE
3 A,B,C,D Wasser wird warm
Die Grafik zeigt, wie sich das Volumen von 1 dm³ Wasser bei Erwärmung, ausgehend von 0°Celsius,
verändert.
a) Beschreiben Sie an Hand des Grafen die Volumenänderung von 1 dm³ Wasser in
Abhängigkeit von der Temperatur.
b) Lesen Sie aus dem Grafen ab, bei welcher Temperatur das Wasservolumen auf ein Minimum
absinkt (= Anomalie des Wassers.)
c) Kreuzen Sie an, welchem allgemeinen Funktionstyp der abgebildete Graph zugeordnet
werden kann, und begründen Sie Ihre Wahl.
Funktionstyp
f(x) = ax² + b
f(x) = ax² + bx + c
f(x) = ax² + bx
f(x) = ax²
Begründung




d) Geben Sie an, was Sie über den Koeffizienten a im Funktionsterm der abgebildeten Funktion
aussagen können.
e) Ermitteln Sie eine Termdarstellung der abgebildeten Funktion.
f) Erklären Sie eine Methode zur Berechnung des Scheitels der abgebildeten Kurve und
berechnen Sie diesen.
g) Skizzieren Sie mögliche Kurvenverläufe für f(x) = ax² + b in Abhängigkeit von a, b  R
(a, b ≠ 0).
6
Aufgabenpool für angewandte Mathematik / 2. Jahrgang
Bundes-ARGE
Lösungserwartung:
a) Interpretieren: Im Intervall [0; 4] nimmt die Volumenänderung ab und in Intervall [4; 11]
nimmt sie zu.
b) Interpretieren: Bei 4°C befindet sich das Minimum und dies entspricht dem Scheitel des
Graphen.
c) KFunktionstyp
r
f(x) = ax² + b
e
f(x) = ax² + bx + c
u
f(x) = ax² + bx
z
e
f(x) = ax²
Begründung (Argumentieren)


x
Parabel mit zwei Nullstellen, eine davon liegt im
Koordinatenursprung (Produkt-Null-Satz)

d) Argumentieren: a > 0, weil die Parabel nach oben geöffnet ist.
e) Operieren, Modellieren: Punkte: N(8|0) und P(1|-50)  f(x) = ax² + bx
0 = 64 a + 8 b
-50 =
a + b / (-8)
oder händisch:
400 = 56 a
Technologieeinsatz möglich
400 50

56
7
50  400

b =  50 
7
7
50
400
x² 
x
f(x) =
7
7
a=
f) Argumentieren: Die x-Koordinate des Scheitels liegt zwischen den beiden Nullstellen und es
gilt
x=
a b 08

=4
2
2
und
y = f(4) = -114,2867
g) Operieren
a > 0;
b>0
a > 0;
b<0
a < 0;
b>0
a < 0;
b<0
7
S(4/-114,3)
Aufgabenpool für angewandte Mathematik / 2. Jahrgang
Bundes-ARGE
3A,C Bevölkerung in den USA
Beschreiben und interpretieren Sie die Bevölkerungsentwicklung in den USA an Hand folgender
graphischer Darstellung!
Quelle: http://www.angeredbrackets.com/2009/05/measuring-copyright-duration-in-manyears-the-only-way-it-really-matters/ [Stand: Dezember 2010]
a) Entnehmen Sie die Bevölkerungszahl in den Jahren 1910, 1930, 1970 aus der Grafik!
b) Nähern Sie diese Bevölkerungsentwicklung mit einer quadratischen Funktion an. Hinweis:
Setzen Sie für die Berechnungen das Jahr 1790 als Zeitpunkt 0. Bestimmen Sie daraus, wann
die Bevölkerungszahl 150 000 000 Menschen betragen wird.
c) Zeichnen Sie die Näherungskurve!
d) Bestimmen Sie die absolute und die prozentuelle Bevölkerungsentwicklung zwischen 1900
und 2000 aus der Näherungskurve!
8
Aufgabenpool für angewandte Mathematik / 2. Jahrgang
Bundes-ARGE
LÖSUNG:
a) Interpretieren 1910: 90 000 000
1930: 120 000 000
1970: 200 000 000
b) Operieren: Quadratische Funktion: y = f(x) = ax2 + bx + c
f(x) = 150 000 000 einsetzen und mit Technologie bestimmen: x = 156, 62
1 970 + 157 = 2 127
Im Jahre 2 127 erwartet man in den USA bei gleichbleibendem Trend 150 Mio. Menschen.
c) und d) Interpretieren und Operieren
d)
Jahr 1910: f(120) = 90 000 000
Jahr 1930: f(140) = 120 000 000
Jahr 1970: f(180) = 200 000 000
Prozentuelle Bevölkerungsentwicklung zwischen 1900 und 2000: ca. 250 Prozent
Absolute Bevölkerungsentwicklung zwischen 1900 und 2000: ca. 200 000 000
9