Aufgaben3

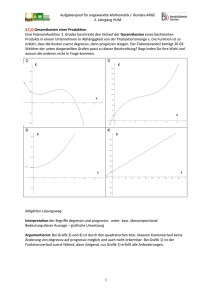
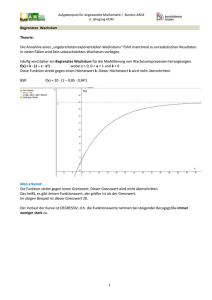
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
3A,B,C Wirtschaftsmathematik auf Stufe des 2. JG
Zwischen dem Verkaufspreis p eines Artikels und der verkauften Menge x besteht folgender linearer
Zusammenhang:
3
x
2
p = 360 -
(Preis-Absatz-Funktion)
a) Unter dem Erlös versteht man die Funktion E = p  x. Geben Sie die Erlösfunktion an und stellen
Sie sie grafisch dar. Berechnen Sie, wann der Erlös gleich Null ist.
b) Bei wie viel verkauften Stück beträgt der Erlös genau € 21.000,-?
c) Bei wie viel verkauften Stück ist der Erlös maximal und wie hoch ist er dann?
d) Die Kostenfunktion beschreibt die gesamten anfallenden Kosten für die Erzeugung von x Stück.
Sie besteht aus Fixkosten, die nicht von der Stückzahl abhängig sind und aus variablen Kosten, die
sich mit der Anzahl der erzeugten Stück x verändern.
Sie ist gegeben: K(x)= 120 x + 5 000.
Zeichnen Sie den Grafen im Schaubild der Erlösfunktion ein und geben Sie in der Grafik die
Fixkosten an.
e) Bestimmen Sie die Funktion der durchschnittlichen Kosten K (x) = K/x ( =Stückkostenfunktion)
und skizzieren Sie ihren Verlauf in einem eigenen Koordinatensystem.
f) Ermitteln Sie die Gewinnfunktion G(x), die sich mit G = E – K bestimmen lässt.
Berechnen Sie die Gewinnzone, d.h. jenen Bereich, in dem ein Gewinn anfällt.
g) Bei wie viel verkauften Stück ist der Gewinn maximal und wie groß ist er dann?
h) Stellen Sie G(x) im Bild von E(x) und K(x) dar und interpretieren Sie den Zusammenhang zwischen
den drei Funktionsgrafen.
Lösung:
a) Operieren: E(x) = p.x = 360x -
360x -
3
x² = 0
2
3
x²
2
x1= 0 x2= 240
b) Operieren 21000 = 360x -
3
x²
2
x1= 100 x2= 140
Bei 100 Stück und bei 140 Stück nimmt man jeweils
21 000 Euro ein.
c)Interpretieren und operieren
Aus der Grafik erkennbar x = 240/2 = 120
E(120)= 21 600
1
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
d) Interpretieren, Operieren: Fixkosten = € 5.000,-
e) Operieren K (x) = K(x)/x = 120 + 5000/x
f) Modellieren, Operieren
G(x)= E(x)-K(x) = 360x G(x) = 0
3
3
x² - 120x-5000 = - x² +240x -5000
2
2
Ein Gewinn ist zwischen 25 und 135 Stück möglich
g) Operieren, Interpretieren: max. Gewinn bei 80 Stück (Scheitel der Parabel) und G(80) = 4 600
f) Interpretation: Schnittpunkte von Kosten- und Erlösfunktion = Nullstellen der Gewinnfunktion
wenn E(x) > K(x) dann G(x) > 0
2
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
3 A,B Fluglinie
Eine kleine Fluglinie hat auf einer bestimmten Strecke mit 60 beförderten Personen volle Auslastung.
Ein Flugticket kostet dabei € 80,-. Um die Einnahmen zu steigern, überlegt die Fluglinie, den
Ticketpreis zu erhöhen. Es wird angenommen, dass pro Erhöhung des Flugpreises um € 2,- eine
Person weniger buchen wird.
a) Stellen Sie die Funktionsgleichung auf, die einen linearen Zusammenhang zwischen Ticketpreis
und Personenanzahl voraussetzt.
b) Stellen Sie die Einnahmen als Funktion der Personenzahl grafisch dar und lesen Sie aus der Grafik
ab, welcher Ticketpreis die größtmöglichen Einnahmen bewirkt.
Lösung
a) Modellieren, operieren (mit oder ohne Technologieeinsatz)
Anzahl der Personen: 60 Personen  Ticketpreis: p = 80 Euro/Person
59 Personen  Ticketpreis: p = 82 Euro/Person
p(x) = ax + b
80 = 60 a + b
82 = 59a + b
 p(x)= -2x + 200
b) Operieren, Interpretieren
Einnahmen = Preis pro Ticket mal Personen ( E = -2x² + 200 x)
grafische Lösung
E(x)= -2x² + 200x quadratische Erlösfunktion (nach unten geöffnet, Scheitel gibt den größtmöglichen
Funktionswert wieder!)
Variante: Grafik vorgeben und interpretieren lassen:
a) Wie wirkt sich eine Preiserhöhung auf die Nachfrage aus?
b) Wie viele Tickets können verkauft werden, wenn der Preis…beträgt?
c) Welcher Preis dürfte höchstens verlangt werden, damit zumindest … Personen den Flug
buchen?
d) Wie hoch ist der Erlös, wenn das Ticket um … verkauft wird?
e) Welcher Erlös wird bei voller Auslastung erzielt?
3
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
3 A,B,D Netbook
Ein Hersteller von Notebooks erkennt aus empirischen Untersuchungen den folgenden
Zusammenhang zwischen Preis/Stück und Absatzmenge:
x Absatz in Stück p
10
30
60
Preis in €/Stück
428
406
328
a) Erstellen Sie eine quadratische Funktion der Form p( x)  a  x ²  b  x  c mit Hilfe der 3 Punkte.
b) Argumentieren Sie, warum schon aus der Angabe klar ist, dass der Koeffizient a negativ sein
muss, bzw. was würde es bedeuten, wenn er positiv wäre?
c) Diskutieren Sie, ob das Modell der quadratischen Gleichung f(x) = - 0,03x² + 0,1x + 430 den
Zusammenhang zwischen Preis pro Stück und Absatzmenge realistisch beschreibt. Erläutern Sie
unter Umständen Mängel des Modells.
Lösung:
a) Operieren und Technologieeinsatz
428 = 100a + 10b + c
406 = 900a + 30b + c
328 = 3600a + 30b + c
Lösung mit Technologie:
p(x) = -
3
x
x² + + 430
100
10
b) Argumentieren
Im Allgemeinen hat ein höherer Verkaufspreis zur Folge, dass der Absatz zurückgeht, was er laut
Tabelle auch tut.
Positives a würde bedeuten: höherer Preis mehr Absatz (evtl. Snob-Effekt)
c) Argumentieren
Die Preisfunktion hat folgenden Verlauf:
Im Prinzip eignet sich die Funktion im Definitionsbereich
[0, 121] recht gut zur Beschreibung der Abhängigkeit
zwischen Preis und Absatz. Man muss allerdings die
Grenzen des Modells (besonders auf der x-Achse)
beachten.
Wenn man nichts verkauft kann man zwar den Preis mit
430 Euro pro Stück ansetzen – Höchstpreis -, aber sehr
unwahrscheinlich ist es, wenn man den Preis auf 0 setzt,
dass man dann ca. 121 Stück verkauft. Man nennt dies
die Sättigungsmenge, realistisch ist nur, dass dann auf
dem Markt kein Interesse am Produkt mehr besteht.
4
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
3 A, B, C, D Anhänger
In einem Betrieb werden PKW eines bestimmten Typs hergestellt. Die Herstellungskosten für einen
Anhänger können mit 4 Geldeinheiten (= GE) veranschlagt werden. Dazu kommen wöchentliche
Fixkosten von 100 GE. Die Anzahl x (Stück) verkaufter Anhänger hängt vom Verkaufspreis p eines
Anhängers ab: mit zunehmendem Verkaufspreis p werden weniger Anhänger verkauft. Auf Grund
von Marktbeobachtungen konnte man näherungsweise für die Zeitdauer einer Woche den
Zusammenhang p = - x / 20 + 10 finden.
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
l)
m)
Setzen Sie den Wert x = 0 ein und interpretieren Sie das Ergebnis!
Setzen Sie p = 5 ein und interpretieren Sie das Ergebnis!
Werden nur halb so viele Anhänger verkauft, wenn der Preis von 4 auf 8 GE/ME verdoppelt wird?
Stellen Sie den Zusammenhang zwischen Preis und verkaufter Stückanzahl graphisch dar.
Wenn der Erlös berechnet wird mit E(x) = p(x)  x, wie lautet die Erlösfunktion für dieses spezielle
Beispiel?
Stellen Sie die Erlösfunktion graphisch dar!
Bei welcher Stückzahl hat man den größten Erlös? Begründen Sie
Ihr Ergebnis.
Erklären Sie, warum der Erlös nicht als Gewinn verstanden werden kann.
Erstellen Sie aus der Angabe die (lineare) Kostenfunktion!
Gewinn = Erlös - Kosten: Wie lautet hier die Gewinnfunktion?
Stellen Sie die Gewinnfunktion graphisch dar!
Was bedeuten die Nullstellen der Gewinnfunktion?
Bei welcher Stückzahl ist der Gewinn am größten?
Lösung:
a) Operieren, Interpretieren: p(0) =10 GE heißt:
kein Anhängerverkauf bei Stückpreis von 10 GE
b) Operieren, Interpretieren: 5 = - x /20+10
x =100
Bei einem Preis von 5 GE werden 100 Anhänger
verkauft.
c) Operieren, Interpretieren: Preis = 4  4 = - x /20+10 
x = 120;
Preis verdoppeln  8 = - x /20+10  x = 40
Die Anzahl wird nicht halbiert.
d) Siehe Nebenspalte
e) Modellieren: E(x) = - 0,05x² + 10x
f) Siehe Nebenspalte
g) Operieren und argumentieren: bei x = 100 ( Scheitel –b/2a =
10/0,1=100)
h) Argumentieren: Der Erlös gibt die Einnahmen wieder, davon sind
aber die Herstellungskosten abzuziehen, dann erst erhält man den
Gewinn.
i) Modellieren: K(x) = 4x + 100
j) Modellieren: G(x) = -0,05x² + 6x-100
k) Siehe Nebenspalte
l) Interpretieren: N(20/0) und N(100/0). Es müssen zwischen 20 und
100 Anhänger verkauft werden, um Gewinn erzielen zu können.
m) Interpretieren: Bei 60 verkauften Anhängern ist der Gewinn am
größten.
Zu d)
zu f)
zu k)
5
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
3 A,B,C,D Produktion
Die Produktionskosten einer Ware können annähernd durch die folgende quadratische Funktion
beschrieben werden: K(x) = 0,005x³ + 0,44x +512.
Der Verkaufspreis pro Stück beträgt konstant 4 GE.
a) Erstellen Sie die Erlösfunktion! (E = px)
b) Stellen Sie die Kosten- und die Erlösfunktion grafisch dar.
(Günstige Fenstereinstellungen: x: -500 bis 800, y: -200 bis 2500!)
c) Geben Sie die Gewinnfunktion (G = E – K) an, stellen Sie G(x) ebenfalls grafisch dar.
d) Ermitteln Sie grafisch die Schnittpunkte von K(x) mit E(x) und die Nullstellen von G(x).
Was fällt Ihnen auf? Begründen Sie Ihre Erkenntnis!
Wie nennt man den Bereich zwischen den beiden Nullstellen von G(x)?
e) Skizzieren Sie den Graphen der Gewinnfunktion! Verwenden Sie für eine aussagekräftige Skizze
mindestens drei signifikante Punkte des Graphen.
Kennzeichnen Sie die Gewinnzone in Ihre Skizze!
(Günstige Fenstereinstellungen: x: 0 bis 600 y: -100 bis 200)
f) Bei welcher Stückzahl wird der maximale Gewinn erzielt und wie groß ist er?
g) Für welche Stückzahl beträgt der Gewinn mindestens 100 GE?
Lösung:
a) Modellieren: E ( x)  4 x
b) und c) Operieren und Technologieeinsatz
G ( x)  E ( x)  K ( x)
G ( x)  0,005 x 2  3,56 x  512
6
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
d) Operieren, Technologieeinsatz und Argumentieren
Schnittpunkte von K(x) und E(x): S1=(200|800), S2=(512|2048)
Nullstellen von G(x): N1 (200|0), N2 (512|0)
Die x-Koordinaten der Schnittpunkte und Nullstellen sind ident. Sind Erlös und Kosten gleich hoch, so
arbeitet der Betrieb genau kostendeckend. Es wird somit weder ein Gewinn noch Verlust erzielt,
deshalb sind diese Punkte auch die Nullstellen von G(x)!
Den Bereich zwischen den beiden Nullstellen von G(x) nennt man Gewinnzone!
e)Operieren und
Interpretieren
signifikante Punkte:
N1 (200|0), N2 (512|0),
Max(356|121,68)
f) Technologieeinsatz
Maximaler Gewinn:
Der maximale Gewinn in Höhe von 121,68 GE wird bei 356 Stück erzielt.
g) Interpretieren und argumentieren
Schnittpunkte zwischen der
Hilfslinie y =100 und der
Gewinnfunktion mit
Technologie ermitteln:
S1 (290,15|100)
S2 (421,85|100)
Im Bereich von 291 bis 431
produzierten und
verkauften Stück beträgt
der Gewinn mindestens
100 GE.
7