Wachstumsfunktionen1

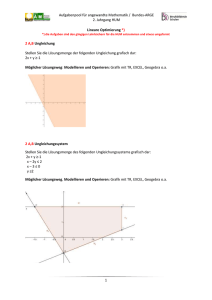
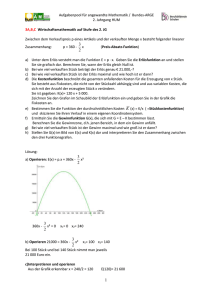
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
Wachstums- und Zerfallsfunktionen (linear und exponentiell)
Wichtig: das Rechnen mit Exponentialtermen muss zuerst mit normalen Rechenaufgaben
nach den üblichen Lehrbuchaufgaben eingeübt werden!
3 A,B, D Regenwald
Aus vielen Gründen (Gewinnung von Tropenhölzern, Rodung für Weideflächen, …) nimmt der
Regenwaldbestand jährlich um ca. 4% ab.
a) Argumentieren Sie, ob hier lineare oder exponentielle Abnahme oder etwas anderes vorliegt.
b) Erstellen Sie ein mathematisches Modell für diesen Abnahmeprozess.
c) Berechnen Sie, wie lange es dauert, bis ein gewisser Waldbestand von 110 000 m3 Holz auf
82 660 m3 zurückgeht.
d) Wie lange dauert es (unabhängig vom Anfangswert), bis sich der Holzbestand halbiert?
Lösung:
a) Argumentieren:
Wenn in gleichen Zeitabständen der gleich große Prozentsatz i des Bestandes B verschwindet, so
handelt es sich um eine exponentielle Abnahmefunktion B(n).
Begründung:
Bestand zu Beginn: B0
Nach 1 Jahr B(1) = B0 (1 - i)
Nach n Jahren B(n) = B0 (1 - i)n …Exponentialfunktion.
b) Transferieren und Modellieren:
möglich: Tabelle, Schrumpfungsfaktor, Exponentialgleichung, richtige Formel aus der
Formelsammlung
B(n) = 100 · 0,96n Bestand in Prozent, Anfangswert 100 %
Oder :
B(n)= 100 · e -0,0408 n
c) Operieren und Technologieeinsatz:
Möglicher Lösungsweg: Anfangswert B0 = 110 000
m(t) = m(0) . qt
q = 96% = 0,96
t
82 660 = 110 000 . 0,96 …. Technologieeinsatz, oder
0,96t = 82 660/110 000
/ log
t. log 0,96 = log 0,751 454 545
t = log 0,751 454 545/log 0,96
t = 6,999  7 Jahre
d) m(0)/2 = m(0) . qt
0,5 = 0,96t
t . log 0,96 = log 0,5
t = log 0,5/log 0,96 = 16,979  17 Jahre
1
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
3 A, B,C Wassertonne
In einer zylindrischen Wassertonne, in der sich bereits 20 l Wasser befinden, fließt gleichmäßig Wasser zu.
Pro Minute fließen 3 l zu.
a) Gib eine Formel für die Wassermenge V nach der Füllzeit von t min. an.
b) Stelle das Volumen V der Tonne abhängig von der Zeit t grafisch dar und lies ab, wann die Tonne
50 Liter fasst.
c) Eine zweite zylindrische Wassertonne ist leer, aber pro Minute fließen 5 Liter zu.
Wann fasst diese Tonne gleich viel wie jene Wassertonne, in der sich bereits 20 l Wasser befinden
und in die pro Minute 3 l zufließen?
Lösung:
a) Modellieren
V  0   20  20  N0
V 1  23  23  k  20  k  3
V  t   3t  20
b) Operieren, Interpretieren
nach 10 min fasst die Tonne 50 Liter.
2
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
c) Operieren, Interpretieren
Rechenart frei, hier Geogebra:
t in min
Nach 10 min sind beide Tonnen gleich voll.
3
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
3 A,B,C,D
Salmonellen
Bei einer Feier wird Kartoffelsalat angeboten. Um 15 Uhr sind in 100 g bereits 5 000 Salmonellen
vorhanden. Bis zur Verwendung wird der Salat so gelagert, dass sich unter diesen Bedingungen die Anzahl
der Salmonellen in 2 Stunden 36 Minuten verdoppelt.
a. Stellen Sie eine Funktionsgleichung auf, welche den Wachstumsprozess in Abhängigkeit von der Zeit,
beschreibt!
b. Berechnen Sie die prozentuelle Zunahme pro Stunde.
c. Die Anzahl der Salmonellen um 18:30 Uhr und 21:06 Uhr erlauben die Ermittlung der Verdopplungszeit.
Begründen Sie, warum dies möglich ist und geben Sie die Verdopplungszeit an.
d. 3 Millionen Salmonellen können zu ernsthafter Erkrankung führen.
Die Graphik zeigt den Verlauf der Wachstumsfunktion. Interpretieren Sie anhand der Grafik, wann
dieser Wert überschritten wird! In welcher Zeitspanne verzehnfacht sich die Anzahl der Salmonellen?
e.
Möglicher Lösungsweg:
a) Operieren
2  e2,6
  ln(2):2,6
  0,266595
N(t)  5000  e0,266595t
b)Operieren
auf die Form bringen: N(t) = 5 000 · at
N(t)  5000 1,3055117t
Ablesen von a: 30,55 %
4
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
c) Operieren, Argumentieren
N(3,5)  5000  e3,5  12711 N(6,1)  5000  e6,1  25423
Die Anzahl der Salmonellen hat sich verdoppelt. Das bedeutet, die Zeitspanne entspricht genau der
Verdoppelungszeit. 6,1 – 3,5 = 2,6 Stunden
d) Interpretieren
Verschiedene Lösungswege möglich, am besten mit Technologie
Ablesung ergibt ca. 24 h
In ca. 24 Stunden sind etwa 3 Mio. Salmonellen im Salat zu erwarten.
Ablesung: 22,4 - 13,8 = 8,6 h
Alle ca 8 ½ Stunden verzehnfacht sich die Zahl der Salmonellen
5
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
3 A,B Attersee
Der Attersee ist 171 m tief, seine Oberfläche liegt auf 469 m Seehöhe. Der Druck im Wasser nimmt alle 10 Meter um
ungefähr 1 Bar (bar)zu. Der Luftdruck p ist von der Meereshöhe h abhängig und wird mit der folgenden Formel
beschrieben:
h
p(h)  1,013  0,5 5500
h … Meereshöhe in Meter (m)
p … Druck in bar
a) Berechnen Sie, wie hoch der Gesamtdruck am tiefsten Grund ist.
b) Stellen Sie die Funktionsgleichung auf, die den Druck im Wasser beschreibt.
LÖSUNG
a)Operieren
469
5500
f(469)  1,013  0,5
 0,955 bar
Wasserdruck in 10 m Tiefe: 1,955 bar
Der Wasserdruck in 171 m Tiefe beträgt ungefähr 18,055 bar.
b) Modellieren
p(0) = 0,955, p(10) = 1,955
Es handelt sich um eine lineare Funktion, daher
p(h) = k · h + d
d = 0,955, 1,955 = k · 10 + 0.955  k = 0,1
p(h) = 0,1h + 0,955
3 B, D Energiebedarf
In einer Region wurden im Jahr 2000 560,3 TWh ( = Terawattstunden = 1012 Wattstunden) verbraucht, im Jahr 2007
609,37 TWh. Die vorhandenen Kapazitäten reichen bis 711 TWh.
a) Ein Energieunternehmen nimmt an, dass der Energieverbrauch in den nächsten 13 Jahren wie in den 7 Jahren
davor, linear weiter steigt. Ermitteln Sie eine Prognose für den zukünftigen Verbrauch.
Argumentieren Sie, ob ein zusätzliches Kraftwerk benötigt wird.
b) Eine Bürgerinitiative behauptet, der Energieverbrauch steigt exponentiell. Sie möchte, dass ein zusätzliches
Kraftwerk mit mindestens 1,2 TWh gebaut wird, um in den nächsten 13 Jahren den zukünftigen Bedarf decken zu
können.
Ermitteln Sie eine Prognose für den zukünftigen Verbrauch unter diesem Aspekt.
Argumentieren Sie, ob diese Initiative das zusätzliche Kraftwerk in der angegebenen Größe zu Recht fordert.
Lösung
609,37  560,3
 7,01 ; f(2020)  609,37  13  7,01  700,5 TWh
7
Es ist bei dem Modell einer linearen Zunahme kein neues Kraftwerk nötig.
a) lin.W.: : k 
13
 609,37  7
b) exp.W.: : f(2020)  609,37  
  712,19 TWh
 560,3 
Es ist das neue Kraftwerk bei dem Modell des exponentiellen Wachstums nötig. Bei 1,2 TWH mehr, würden die
Kapazitäten für die nächsten 13 Jahre ausreichen.
6
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
3 A,B,C,D Insekten
Die Grafik zeigt das Anwachsen einer Insektenpopulation innerhalb von 10 Tagen.
a) Interpretieren Sie anhand der Grafik den Anfangswert
y(0).
Geben Sie die Zeit an, nach welcher sich die Anzahl der
Insekten verdreifacht.
b) Argumentieren Sie, welche Form von Wachstum hier vorliegt: Lineares oder exponentielles Wachstum.
c) Erstellen Sie mithilfe von 2 abgelesenen Werten eine
geeignete Wachstumsfunktion.
Berechnen Sie, nach wie vielen Tagen sich der
Anfangsbestand verzehnfacht hat.
Lösungen
a) Interpretieren
y(0) = 30
Zu Beginn waren 30 Insekten
y(6) = 90 nach 6 Tagen hat sich der Anfangsbestand verdreifacht.
b) Argumentieren
Es liegt ein exponentielles Wachstum vor, denn es ist kein konstanter Zuwachs pro Zeiteinheit und die Werte b
bilden bei gleichen Zeitabständen eine geometrische Folge:
Aus den Werten für den Beginn, nach 5 und nach 10 Tagen: b(0) = 30, b(1) = 36, b(2) = 43 folgt:
36 /30 ≈ 1,2 und 43/36 ≈ 1,2 … annähernd gleicher Quotient bei gleichen Zeitabständen.
Daher gilt die Formel für die geometrische Folge b(n) = b(0) · qn mit q ≈1,2
Das ist eine Exponentialfunktion.
c) Modellieren und Operieren
b(n) = a · b n
Einsetzen: n = 0 und n = 5 weil sie gut ablesbar sind 
75 = 30 · b5
b = 1,201
Der Insektenbestand kann annähernd mit der Funktionsgleichung: b(n) = 30 · 1,201n mit n Є N beschrieben
werden.
b(n) = 300 = 30 · 1,201n  n = 12,57
Am 13. Tag hat sich die Population nach diesem Modell verzehnfacht.
7
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
3 A,B,C,D Radioaktiver Zerfall
In einer Menge des radioaktiven Isotops Plutonium
zerfallen.
243
Pu sind nach 3 Stunden bereits 34% der vorhandenen Kerne
a) Geben Sie das Zerfallsgesetz in der Form N(t) = N0 · e-λt sowie in der Form N(t)= N0 · at an.
b) Berechnen Sie die Halbwertszeit  und begründen Sie, warum die Halbwertszeit von der Anfangsmenge
unabhängig ist.
c) Skizzieren Sie die Funktion und interpretieren Sie anhand der Grafik, wie viel von der anfänglichen Masse von 10 g
234
Pu nach sieben Stunden noch vorhanden sind.
d) Argumentieren Sie, wann das Element komplett verstrahlt sein wird.
Lösung:
a) Operieren und Technologieeinsatz
N0 = 100% … Anfangswert
Nach 3 Stunden N = 66%  66 = 100 · e -3λ  λ = 0,138
N(t)=100 · e-0,1385t
oder N(t)= 100 · 0,87 t N(t) ist in Prozent des Anfangswert angegeben, t in Stunden.
b) Operieren und Argumentieren
50 = 100 · e-0,1385t
 ln(0,5) = - λ   = - ln(0,5)/ λ = 5 h
Die Halbwertszeit gibt an, wann die Hälfte der gerade vorhandenen Menge abgebaut ist. Dies ist unabhängig davon
wie viel Menge zu Beginn vorhanden ist.
Mathematisch gesehen kürzt sich in der Gleichung die Anfangsmenge heraus:
N0
 N0  e
2
d) Argumentieren:
c) Operieren und interpretieren
Man kann aus der Grafik erkennen,
dass die Kurve allmählich gegen 0 geht.
Betrachtet man die Gleichung
N(t)= 10 · 0,87 t, dann gilt für hohe
Werte von t, dass sich N zwar der Null
nähert, dass N aber niemals exakt 0
wird.
t = 100 h  N = 8,9 · 10 -5 g
t = 1000 h  N = 3 · 10-59 g
t ∞, N = 0 … Grenzwert.
Nach sieben Stunden sind von 10 g noch ca. 3,8 g vorhanden.
8
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
3 A,B,C,D Exponentielle Temperaturverläufe
Ein Körper wird in einen Kühlraum gestellt und kühlt exponentiell ab, wobei für die Temperatur
T in Grad Celsius (°C) nach t Minuten gilt:
T(t) = 80 · 0,85 t
Der folgende Graph zeigt diesen Kühlungsprozess:
a) Interpretieren Sie anhand des Graphen, welche Temperatur der Körper zu Beginn, nach 3 bzw. nach 5 Minuten
hatte und wann die Temperatur nur mehr halb so groß wie zu Beginn ist.
3C
b) Überprüfen Sie alle diese Werte von a) rechnerisch mit Hilfe der angegebenen Funktionsgleichung.
3B
c) Argumentieren Sie, um wie viel Prozent die Temperatur pro Minute abnimmt und wie weit die Temperatur des
Körpers höchstens sinken kann.
3 D,C
d) Argumentieren Sie, wie der Temperaturverlauf für eine exponentielle Erwärmung aussehen muss, wenn ein 20°C
warmer Körper um 12 % pro Minute erwärmt wird.
3D
t
e) Erklären Sie, was die Basis a bei einer Abkühlung bzw. Erwärmung nach der Funktionsgleichung T(t) = c · a
generell aussagt und wie groß sie sein muss.
3D
Lösung:
a) Interpretieren anhand der Grafik:
zu Beginn 80°C
T(3) = ca. 49°C
T(5) = ca. 35°C
Halb so groß: nach ca. 4 min
b) Operieren
zu Beginn: T(0) = 80.0,850 = 80
T(3) = 80.0,853 = 49,1°C
T(5) = 80.0,855 = 35,5°C
halb so groß:
40 = 80.0,85t
0,5 = 0,85t
log 0,5 = t.log0,85
log(0,5)
t
 4,3min
log(0,85)
c) Argumentieren, Interpretieren
Pro Minute sinkt sie um 15%
Aus der Grafik: 100 % … 80°
85% … 68° nach 1 Minute
Unterschied 15%
Oder: 100% …30°, 25,5° nach 1 Minute … 85%
Unterschied 15%
Die Temperatur kann nur bis zur Umgebungstemperatur sinken. Also bis
zur Temperatur im Kühlraum. (im Beispiel: 0°C)
d) Argumentieren
Die Funktion hat den Anfangswert 20°, steigt dann monoton nach der
Gleichung: T(t) = 20 · 1,12t
T in °C und t in Minuten.
e) Argumentieren: Die Basis a gibt das prozentuelle Wachstum an:
1+ p/100 im Falle einer Zunahme und 1- p/100 im Falle einer Abnahme.
9
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
3 A,B,C,D Alkomat
Klaus ist bei Freunden eingeladen. Er trinkt um 19 Uhr 1/4 Liter Wein und misst mittels Alkomat einen
Alkoholspiegel von 0,7‰. Um 22:42 ist die Hälfte seines Alkoholspiegels abgebaut.
a) Stellen Sie die Funktionsgleichung auf, die den Abbau des Alkohols beschreibt.
3A
b) Erklären Sie, um welche Funktion es sich handelt und beschreiben Sie die Eigenschaften dieser
Funktion.
3D
c) Um 24 Uhr trinkt er noch 3/8 Liter Wein. Geben Sie den Alkoholspiegel um 3 Uhr an.
3B
d) Argumentieren Sie, ab welcher Uhrzeit er mit seinem Auto nach Hause fahren darf, nachdem er um
Mitternacht noch 3/8 Liter zu sich genommen hat. Der erlaubte Promillegehalt ist 0,5‰.
3B,C
Lösung:
a) Modellieren und transferieren
N(t) … Alkoholspiegel nach einer bestimmten Zeit t in Stunden
N(0) … Alkoholspiegel zu Beginn um 19 h in Promille
a … Abnahmefaktor
t … Zeit in Stunden
Mit den gegebenen Werten:
a = 0,829
N(t) = 0,7 · 0,829 t
b)
Es handelt sich um eine Exponentialfunktion: hier wird ein Abnahmeprozess beschrieben, a ist dabei
kleiner als 1, der stündliche Abbau beträgt ca. 17%, zu Beginn (ab 19 h) nimmt der Alkoholspiegel rasch ab,
dann langsamer.
c)
Vom ersten Viertel beträgt der Alkoholspiegel um Mitternacht – nach 5 Stunden –
¼ Liter entspricht 0,7‰, daher 3/8 Liter entsprechen 1,05‰
Insgesamt abzubauen sind 1,324.
N(t) = 1,324 · 0,829 3 = 0,754
Der Alkoholgehalt um 3 Uhr beträgt 0,754‰.
d)
t = 5,193 nach 0 Uhr
Er darf selbst im Auto fahrend erst gegen 5:12 Uhr nach Hause fahren.
10
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
3, A,B,C,D Bakterienwachstum
Coli-Bakterien vermehren sich im menschlichen Darm durch Zellteilung nach einer exponentiellen
Wachstumsfunktion f(t) = a · bt.
a) Die nach t Minuten vorhandene Anzahl f der Bakterien zeigt folgende Wertetabelle.
t = Minuten
0
20 40 60 80 100
f = Bakterienanzahl in
Tausend Stück
1
2
4
8
16 32
Stellen Sie den funktionalen Zusammenhang in Form einer Funktionsgleichung f(t) dar und geben Sie
die prozentuelle Zunahme pro Minute an.
3A,C
b) Argumentieren Sie die Lösung der folgenden Gleichung im Zusammenhang mit dem Wachstum von Bakterien.
t
20
3
 59049
c) Interpretieren Sie, welchen Sachverhalt die folgenden Funktionsgleichungen ausdrücken.
f wird in Tausend Stück angegeben und t in Minuten.
f(t) = 0,5
0,1t
f(t) = 10 ∙
Lösung
a) Modellieren und Interpretieren
Um die Gleichung zu finden, sind mehrere Methoden möglich:
am einfachsten mit Regression (EXCEL oder Taschenrechner)
Das liefert f(t) = 1,0353t.
Im Falle, dass man über diese Kenntnis noch nicht verfügt, können Tabellenwerte herangezogen werden:
f(0) = 1, f(100) = 32 können eingesetzt werden.
32 = 1 · a 100  a = 32 1/100
Das liefert das gleiche Ergebnis.
Pro Minute beträgt die Zunahme ca. 3,5%.
(andere Erklärung: Verdoppelung nach jeweils 20 Minuten  2 1/20 = 1,0353 )
b) Operieren, Argumentieren
t
20
3
 59049
Die Lösung dieser Gleichung : t = 200 Minuten
Die Aussage bedeutet, dass nach 200 Minuten die Bakterienanzahl auf 59 049 Mengeneinheiten angewachsen ist.
11
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
c) Interpretieren
Am besten kann man interpretieren, wenn man sich jeweils eine Skizze anfertigt, ist aber nicht
erforderlich.
Die Funktion f mit f(t) = 0,5 0,1t beschreibt eine
Abnahme mit einer Halbwertszeit von 10 Minuten und
ist daher für den vorliegenden Fall nicht passend.
Bei der Funktion mit
f(t) = 10 ∙
handelt es sich um eine Zunahme, mit dem
Anfangswert von 10 000 Bakterien.
Die Verdopplungszeit beträgt ca. 31 Minuten.
Diese Funktion könnte durchaus ein
Bakterienwachstum beschreiben.
12
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
Anwendungsaufgaben zu Wachstums- und Abnahmeprozessen von Theresia Klonner
Überarbeitung aus Josef Laub, Lehrbuch der Mathematik für Bildungsanstalten 3; Wien 1987 (ISBN 3-209-00682-2), SS. 63, 64, 86
ABC Holzbestand eines Waldes
Der Holzbestand eines Waldes nimmt jährlich um 8 % zu.
a) Derzeit beträgt der Holzbestand rund 17 000 m³.
Berechne den Holzbestand in 3,5 Jahren, wenn nichts
geschlägert wird.
b) Berechne, wie lange es dauert, bis sich der Holzbestand
verdoppelt.
c) Der Graph zeigt das Holzwachstum eines anderen Waldes.
Ermittle grafisch den Holzbestand dieses Waldes nach 8
Jahren.
Lies aus dem Graphen ab, wann dieser Wald einen Bestand
von 20 000 m³ hat.
d) Wieder ein anderer Wald hatte anfangs einen Holzbestand
von 30 000 m³. Nach 10 Jahren wurden
5 000 m³ geschlägert.
Erstelle eine Gleichung, mit der du den Holzbestand dieses
Waldes nach 12 Jahren berechnen kannst.
Lösung
a) 8 % jährliche Zunahme: Vn = V0  1,08n
V3,5 = 17 000  1,083,5
V3,5 = 22 255,228…
In 3,5 Jahren wird der Wald rund 22 255 m³ Holz haben.
b) Verdopplung: 2V0 = V0  1,08n
2 = 1,08n /ln
ln(2) = n  ln(1,08)
n = ln(2) / ln(1,08) = 9,006…
Es dauert etwa 9 Jahre, bis sich der Holzbestand verdoppelt hat.
c)
Nach 8 Jahren hat der Wald ca. 28 000 m³ Holz.
Nach ca. 3,7 Jahren hat der Wald 20 000 m³ Holz.
d) V12 = [(30 000  1,0810) – 5 000]  1,08²
13
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
B D Bakterienkultur
Bakterien vermehren sich durch Teilung. In einer bestimmten Bakterienkultur beträgt die Verdopplungszeit
17 Minuten.
a) Argumentiere, ob sich die der Vorgang der Bakterienteilung durch eine Folge oder durch eine Funktion
mathematisch exakt beschreiben lässt.
b) Nach 2 Stunden wurden 150 000 Bakterien gezählt.
Berechne, wie viele Bakterien ursprünglich vorhanden waren.
c) Stelle die Zunahme der Bakterienzahl in den ersten 2 Stunden grafisch dar. Gehe dabei von einem
Anfangswert von 80 Stück aus.
Lies aus dem Graphen ab, wie viele Bakterien nach 85 Minuten gezählt werden.
Lies ab, nach welcher Zeit 10 000 Bakterien vorhanden sind.
Lösung
a) Der Unterschied zwischen Funktion (D = R) und Folge (D = N) liegt in der Definitionsmenge.
Es handelt sich beim Bakterienwachstum (Teilungen) genau genommen um eine geometrische Folge.
Startwert: n0
1. Glied: n0  a, 2. Glied: n0  a2, usw.
Die Exponentialfunktion ist die Trägerfunktion der Folge.
b) nt = n0  at
2 = 1  a17
a =
= 1,041616011
1,041616120
waren ursprünglich vorhanden
Bei Verwendung eines grafikfähigen Taschenrechners reicht
Eine angemessene Ableseungenauigkeit ist zu tolerieren.
150 000 = n0 
n0  1 125 Bakterien
eine Handskizze.
Nach 85 Minuten werden ca. 2 700 Bakterien gezählt.
10 000 Bakterien sind es nach ca. 115 Minuten (nicht ganz 2 Stunden).
ABD Bevölkerungswachstum (A, B, D)
Die Bevölkerung einer Stadt wächst exponentiell.
a) Im Jahr 1980 hatte eine Stadt ca. 35 000 Einwohner, 2000 waren es bereits 48 000.
Erstelle eine Formel, mit der du die Einwohnerzahl dieser Stadt für ein bestimmtes Jahr abschätzen kannst.
b) Die Bevölkerung einer anderen Stadt wächst jährlich um 1,5 %. Im Jahr 1990 hatte diese Stadt ca.
40 000 Einwohner.
Berechne die zu erwartende Einwohnerzahl für 2020 (auf Hunderter gerundet).
c) Erkläre, wie du berechnen kannst, wann die Stadt aus b) die 50 000-Einwohner-Grenze überschritt.
Lösung
a) nt = n0  at
nimm t = 0 für das Jahr 1980
48 000 = 35 000  a20
a=
= 1,01591801
b) nt = n0  at
nt = 40 000  1,015t
n30 = 40 000  1,01530 = 62 523,2…
Im Jahr 2020 werden es ca. 62 500 Personen sein.
nt = 35 000  1,01591801t
14
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
c) Setze in die Wachstumsformel für n0 = 40 000 ein, für nt = 50 000, für a = 1,015.
Weil der Exponent t gesucht ist, muss man die Gleichung logarithmieren.
Dann wird noch t ausgedrückt.
ABC Abkühlung (B, A, C)
Die Abkühlung von heißem Wasser auf die Temperatur T erfolgt nach der Formel
T = T1 + (T2 – T1)e-0,05t
T … Temperatur in °C nach t min
t … Zeit in min
T1 … Umgebungstemperatur in °C
T2 … Ausgangstemperatur in °C
a) Heißes Wasser mit einer Ausgangstemperatur von 80°C kühlt bei einer Umgebungstemperatur von 20°C ab.
Berechne die Temperatur des Wassers nach 10 Minuten.
b) Forme die Formel so um, dass du bei gegebenen Temperaturen T, T1 und T2 die Abkühlungszeit berechnen
kannst.
c) Der Graph zeigt die Abkühlung von 90°C heißem Wasser bei einer Raumtemperatur von 21°C in Abhängigkeit
von der Zeit t in min.
Lies aus dem Graphen ab, welche Temperatur das Wasser nach 30 Minuten hat.
Lies aus dem Graphen ab, wann das Wasser auf 60°C abgekühlt ist.
Lösung
a) T = T1 + (T2 – T1)  e-0,05t
T = 20 + (80 – 20)  e-0,05  10
T  56,4°C
b) T - T1 = (T2 – T1)  e-0,05t
/ ln
15
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
c)
Nach 30 min hat das Wasser eine Temperatur von ca. 46°C
Auf 60°C abgekühlt nach ca. 12 min
BD Jodisotop 131
Das Jodisotop J-131 zerfällt mit einer Halbwertszeit von 8,05 Tagen.
a) Berechne die Zerfallskonstante .
b) Berechne, wie lange es dauert, bis nur noch 1 % der Ausgangssubstanz vorhanden ist.
c) Erkläre, wie du berechnen kannst, wie viel % der Ausgangsmasse nach 30 Tagen zerfallen sind.
Lösung
a) n(t) = n0  e-t
0,5 = e-.8,05
ln 0,5 = - . 8,05
 =-
= 0,08610524
b) 0,01 = e- 0,08610524 . t
ln 0,01 = - 0,08610524 . t
t=
= 53,483…
Nach ca. 53,5 Tagen ist noch 1 % radioaktives Jod vorhanden.
c) Setze in das allgemeine Zerfallsgesetz den Wert für  und für t = 30 ein.
Berechne n(t), das ist eine Dezimalzahl zwischen 0 und 1
mit 100 multiplizieren  %
16
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
BD Luftdruck
Der Luftdruck hat auf Meereshöhe den Wert p0 = 1,013 bar. Er sinkt mit zunehmender Höhe und kann mit folgender
Funktion beschrieben werden:
p(h) = p0  e-0,125h
h … Höhe in km
a) Stelle den Luftdruck in Abhängigkeit von der Höhe für 0 km  h  9 km grafisch dar.
Lies aus dem Graphen ab, welcher Höhe ein Luftdruck von 0,8 bar entspricht.
Lies den ungefähren Luftdruck bei einer Höhe von 5 000 m ab.
b) Berechne den Luftdruck in einem Bergwerksschacht, der 1 200 m unter dem Meeresspiegel liegt.
c) Erkläre, wie du aus der gegebenen Funktionsgleichung die prozentuelle Abnahme je Kilometer herausfinden
kannst.
Lösung
a)
0.8 bar  Höhe  1,7 km (= 1 700
m)
5 000 m = 5 km  Luftdruck  0,55 bar
b) p = 1,013  e-0,125 . (-1,2)
p = 1,16183… bar
c) Berechne e-0,125 = 0,8824…
muss < 0 sein, weil negativer Exponent
0,88  88 %, das entspricht einer Abnahme von 12 %
ABD Radioaktiver Zerfall von Radium
Die Mengenabnahme eines radioaktiven Stoffes wird als radioaktiver Zerfall bezeichnet.
Von m0 Milligramm (mg) Radium sind nach t Jahren noch m = m0  e-0,000428t mg vorhanden.
a) Berechne, wie viel mg Radium von ursprünglich 3 mg nach 1 000 Jahren noch nachweisbar sind.
b) Forme die gegebene Formel so um, dass du aus einer derzeit vorhandenen Radiummenge und einer
bekannten Zeitspanne auf die Ausgangsmenge schließen kannst.
c) Erkläre, wie du aus der Formel die Halbwertszeit von Radium ermitteln kannst
Lösung
a) m = m0  e-0,000428t
m = 3  e-0,000428  1000 = 3  e-0,428
m = 1,955…  1,955 mg
b) m = m0  e-0,000428t
c)
m = m0  e-0,000428t
setze in die Formel für m =
ein, dann kann man m0 wegkürzen
Nachdem t im Exponenten steht, muss die Gleichung logarithmiert werden
ln(e) fällt weg
t ausdrücken – das ist die Halbwertszeit
17
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
BCD C-14-Methode
Die C-14-Methode wird verwendet, um das Alter von organischen Substanzen (Knochen, Holz, …) zu bestimmen. Der
Anteil des radioaktiven Kohlenstoffisotops C-14 bleibt in lebenden Organismen konstant. Nach dem Tod des
Lebewesens beginnt es zu zerfallen.
a) Der Graph stellt den Abbau des radioaktiven Kohlenstoffisotops C-14 vom Todeszeitpunkt weg dar.
Lies aus dem Graphen die Halbwertszeit ab.
Lies ab, nach wie vielen Jahren ein Tierskelett nur noch 20 % des ursprünglichen C-14-Anteils enthält.
Lies ab, welchen C-14-Anteil Knochenfunde haben, die 8 000 Jahre alt sind.
b) Erkläre, wie du aus dem allgemeinen Zerfallsgesetz n(t) = n0  e-t mithilfe der Halbwertszeit die
Zerfallskonstante  für C-14 berechnen kannst.
c) C-14 hat eine Zerfallskonstante  = 0,000120338.
Berechne, auf welchen Prozentsatz der C-14-Anteil nach 30 000 Jahren gesunken ist.
Lösung
a)
Halbwertszeit: ca. 5 800 Jahre
0,2 = 20 % nach ca. 13 500 Jahren
nach 8 000 Jahren: noch ca. 38 % vorhanden
b) n(t) = n0  e-t
Setze für n(t) gleich n0/2 ein, dann kürzt sich n0 weg.
Setze für t die Halbwertszeit 5760 Jahre ein.
 steht im Exponenten, daher wird logarithmiert (ln wegen „e“)
ln(e) = 1 und fällt weg.
Nun muss man nur noch  explizit ausdrücken.
c)  = 0,000120338
n(t) = n0  e-t
n(t) = e-0,000120338  30 000
n(t) = 0,027…  2,7 %
18