Aufgaben2

Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
Funktionen – Teil2
Funktionsgleichungen
IV 3A,C Gerade und Formel
Welche der angegebenen Formeln ergibt graphisch eine Gerade? Begründen Sie!
1. y = kx +d
2. y = kx² + 2d
3. y = d +2x
4. y = 2kx +d
5. y = d + 2k/x
□ 1., 2. und 3. sind richtig.
□ 1., 3. und 4. sind richtig.
□ Alle sind richtig.
□ 1. und 3. sind richtig.
□ 4. und 5. sind richtig.
Mögliche Lösung: 1,3, und 4 sind richtig
IV 3-C,D Funktionsterm zuordnen
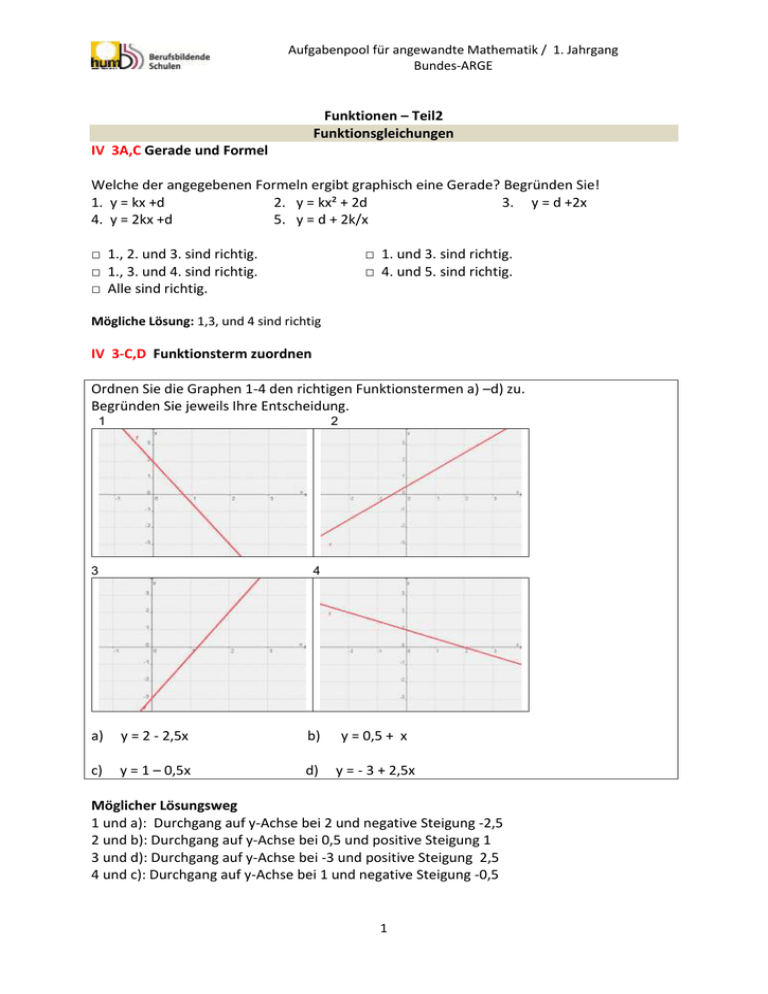
Ordnen Sie die Graphen 1-4 den richtigen Funktionstermen a) –d) zu.
Begründen Sie jeweils Ihre Entscheidung.
1
2
3
4
a)
y = 2 - 2,5x
b)
y = 0,5 + x
c)
y = 1 – 0,5x
d)
y = - 3 + 2,5x
Möglicher Lösungsweg
1 und a): Durchgang auf y-Achse bei 2 und negative Steigung -2,5
2 und b): Durchgang auf y-Achse bei 0,5 und positive Steigung 1
3 und d): Durchgang auf y-Achse bei -3 und positive Steigung 2,5
4 und c): Durchgang auf y-Achse bei 1 und negative Steigung -0,5
1
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3A,B,C,D Graph und Text, passen sie zusammen?
Kreuzen Sie an, welche der folgenden Aussagen mit der Graphik übereinstimmen und welche nicht.
Der Definitionsbereich entspricht jeweils den positiven Werten.
a) Für den Druck eines Plakates werden in einer Druckerei pro Plakat 9 € verlangt.
Zusätzlich werden 1,2 € pro Plakat für das Stecken der Druckplatte verrechnet.
b) Eine junge Frau möchte für ein Fest Namensanstecker bestellen. Die Kosten dafür
betragen 1,2 € pro Anstecker und 9 € Liefergebühr.
c) Für eine Lieferung Frühlingsblumen bezahlt eine Gemeinde 9 € pro Pflanze, für die
Lieferung kommt ein Pauschalbetrag von 1,2 € dazu
d) Ein Pizzalieferant berechnet pro Pizza einen Betrag von 9 €, für die Lieferung
verlangt er 1,2 €.
e) Die Grundgebühr eines Handyanbieters beträgt 9 €, für jede Telefonminute wird
zusätzlich 1,2 € verrechnet.
Möglicher Lösungsweg:
a)
b)
c)
d)
e)
passt nicht, wäre: 9x + 1,2x
passt
passt nicht, wäre: 9x + 1,2
passt nicht, wäre: 9x + 1,2
passt
2
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3-A Was ist eine Funktion, was nicht?
Handelt es sich bei folgenden Zuordnungen um Funktionen? Begründen Sie die Antworten!
a) Den SchülerInnen einer Klasse werden die Katalognummern zugeordnet.
b) Den SchülerInnen einer Klasse werden die jeweils gewählten Freigegenstände
zugeordnet.
c) Den natürlichen Zahlen werden ihre Teiler zugeordnet.
d) Der Zeit nach dem Fallenlassen einer Kugel wir die momentane Höhe zugeordnet.
e) Den Sitzplätzen im Theater wird der Preis für die Karte zugeordnet.
Möglicher Lösungsweg:
a) Funktion: jeder/m SchülerIn wird ein eindeutiger Wert (Katalognummer) zugeordnet
b) Keine Funktion, weil jede/r SchülerIn mehrere Freigegenstände wählen kann.
c) Keine Funktion, weil vielen natürlichen Zahlen mehrere Teiler zugeordnet werden.
d) Funktion, weil zu jedem Zeitpunkt eine eindeutige Höhe zugeordnet werden kann.
e) Funktion, weil jeder Sitzplatz einen eindeutigen Preis hat.
IV 3A,C Graphen interpretieren
Gegeben ist der folgende Graph:
Interpretieren Sie ihn in Bezug
auf:
a) Funktionsgleichung
b) Verhältnis
c) Steigung in %
Möglicher Lösungsweg:
a) y = x/5
b) k = 40:200
c) k = 1/5 = 0,2 = 20%
3
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV – 3A,B,C Funktionsdarstellung
Es sind folgende drei Wertetabellen gegeben:
a) Bei welcher Tabelle könnte eine lineare Funktion vorliegen?
b) Begründen Sie Ihre Entscheidung!
c) Geben Sie die Funktionsgleichungen an, wo es möglich ist!
d) Was fällt bzgl. f(x) und h(x) auf?
e) Zeichnen Sie den Graphen der Funktion f(x) über D = {0; 1; 2; 3; 4;}
und über D = [-4; 4]!
f(x):
g(x):
h(x):
x y
x y
x y
0 8
-3 13
-3 -1
3 14
-2 3
0 5
4 16
0 -5
3 11
1 -3
7 19
Mögliche Lösung:
a) Bei f(x) und h(x) könnte eine lineare Funktion vorliegen.
Bei g(x) liegt keine lineare Funktion vor.
b) Ich lege durch zwei Punkte eine Gerade und wenn die restlichen Punkte auf dieser
Geraden liegen, dann könnte es sich um eine lineare Funktion handeln. Dies trifft bei
f(x) und h(x) zu. Bei g(x) ist dies nicht möglich.
c) f(x) = k ∙ x + d
8 = k ∙ 0 + d => d = 8
14 = k ∙ 3 + d
14 = 3k + 8
|-8
6 = 3k
|:3
k=2
f(x) = 2x + 8
h(x) = k ∙ x + d
-1 = k ∙ (-3) + d
5 = k ∙ 0 + d => d = 5
-1 = -3k + 5
-6 = -3k
| : (-3)
k=2
h(x) = 2x + 5
d) f(x) und h(x) sind parallel, sie haben die gleiche Steigung.
e)
20
15
f ( x)
10
5
4
2
0
x
4
2
4
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3A,B,C,D Zuordnungen verstehen
Die folgenden Tabellen zeigen jeweils den Zusammenhang zwischen zwei abhängigen Größen:
a)
b)
x
y1
x
y2
x
y3
x
y4
1
5
1
12
1
12
1
2
2
7
2
6
2
8
2
4
3
9
3
4
3
4
3
6
4
11
4
3
4
0
4
8
Beschreiben Sie die Abhängigkeiten - falls möglich - durch Funktionsgleichungen und
stellen Sie diese graphisch dar.
Schreiben Sie die zugeordneten Gleichungen in das jeweils richtige Feld der folgenden
Tabelle.
direkt proportional
indirekt proportional
keines von beiden
x und y1
x und y2
x und y3
x und y4
Möglicher Lösungsweg: a) y1 = 2x+3, y2 = 12/x, y3 = -4x + 16, y4 = 2x
b) direkt proportional y = kx, Ursprunggerade, indirekt proportional y = k.
direkt proportional
indirekt proportional
x und y1
keines von beiden
y = 2x+3
x und y2
y = 12/x
x und y3
x und y4
1
Hyberbel
x
y = -4x +16
y = 2x
.
5
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3-A,B,C Lineare Funktion
1) In der Zeichnung ist eine lineare Funktion dargestellt.
Kennzeichnen Sie die Größen k und d, lesen Sie ihren Wert ab und geben Sie die Gleichung
der linearen Funktion an.
Kreuzen Sie die richtigen Aussagen an:
 Je größer die Steigung, umso steiler verläuft die Gerade.
 Je größer die Steigung, umso flacher verläuft die Gerade.
 Die Steigung ist der Quotient von Höhenunterschied zur
waagrechten Entfernung.
 Die Steigung ist der Quotient von waagrechter Entfernung
zum Höhenunterschied.
 In der Gleichung einer linearen Funktion wird mit d der x–
Achsenabschnitt bezeichnet.
 In der Gleichung einer linearen Funktion wird mit d der y–
Achsenabschnitt bezeichnet
2
Möglicher Lösungsweg:
k = 2, d = 1, y = 2x + 1
Richtige Aussagen:
Je größer die Steigung, umso steiler verläuft die Gerade.
Die Steigung ist der Quotient von Höhenunterschied zur waagrechten Entfernung.
In der Gleichung einer linearen Funktion wird mit d der y–Achsenabschnitt bezeichnet
IV 3-A,C Spezielle lineare Funktion
Das Schaubild einer linearen Funktion ist eine Gerade. Wie verläuft eine Gerade, wenn in
der Funktionsgleichung
a) k = 0
b) d = 0 ist?
Skizzieren Sie jeweils eine Gerade für Teil a) bzw. Teil b):
Möglicher Lösungsweg:
Bei k = 0  Gerade ist parallel zur x-Achse, bei d= 0 geht die Gerade durch den Ursprung.
Bsp:
f: y = 4 und g: y = 4x
6
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3-A, C Parallele Geraden
Parallele Geraden erkennt man daran, dass ihre Funktionsgleichungen ……………………
…………………………………………………………………………………………….. .
Gegeben sind vier Geradengleichungen:
g1: y = –3x – 5
g2: 2y = –6x – 5
g3: 5y = –15x + 30
g4: 2y = 6x + 10
Kreuzen Sie die richtigen Aussagen an:
 g1  g3
 g2  g4
 g1  g2
 g1  g4
Möglicher Lösungsweg:
Parallele Geraden erkennt man daran, dass ihre Funktionsgleichungen das gleiche k haben.
g1  g3
g1  g2
IV 3-A, C Punkte
Gegeben sind die Punkte P1(7;6), P2(9;4), P3(1;5)
a) Überprüfen Sie graphisch, ob die drei Punkte auf einer Geraden liegen.
b) Berechnen Sie die Steigung zwischen P1 und P2, bzw. P2 und P3 und interpretieren Sie
das Ergebnis.
c) Erstellen Sie die Gerade g durch P1 und P2 mit Hilfe der Definition der Steigung und
überprüfen Sie rechnerisch, ob der Punkt P3 auf der Geraden liegt.
d) Erstellen Sie die Geradengleichung der zu g parallelen Geraden h durch den Punkt P 3.
Möglicher Lösungsweg:
a) Liegen nicht auf einer Geraden!
b) k(P1,P2) =2/-2 = -1
k(P2,P3) =-1/8
c) y = -x +13 P3 einsetzen : 5 =12 f.A., liegt nicht drauf
d) h : y = -x +6
7
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3- A,B,C Die Normale
a) Lesen Sie die Funktionsgleichung der abgebildeten Funktion f ab.
b) Beantworten Sie grafisch und rechnerisch die beiden Fragen f(-2) = ? und f(x) = -2, x = ?.
c) Ermitteln Sie grafisch und rechnerisch die Gleichung jener Geraden g, die zur Geraden f
normal ist und durch den Koordinatenursprung geht.
Möglicher Lösungsweg:
a)
 y-Achsenabschnitt d = –1
 Die Steigung k ist –1/4, weil „4 nach rechts und 1 hinunter“, also
1
f(x)    x  1
4
1
4
1
2
b) f(–2) = ? und f(x) = –2, x = ?. f(2)    (2)  1    0,5 f(x) = –2  x = 4
Normale: y = 4x
8
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3A,B,C,D Schnittpunkt
Gegeben sind die Gleichungen:
I
2y – x = 4
II
4y – 3x = 7
a) Ermitteln Sie die Lage der Geraden und den Schnittpunkt.
b) Fertigen Sie eine Zeichnung an.
c) Ändern Sie die Gerade II so, dass sie parallel zur Geraden II ist und sie die Gerade I
im Punkt P(3/ 3,5) schneidet.
d) Wo schneiden die Geraden die y-Achse und wie kann man diesen Wert aus der
Angabe ablesen?
Möglicher Lösungsweg:
a) S (1/ 2,5)
b)
c) k= 0,75
3,5 = 3. 0,75 + d  d= 1,25
d) Umformen: y = kx+d d1 = 2 und d2 =
y= 0,75x + 1,25
9
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3-A, C k und d zuordnen
a) Geben Sie für die dargestellten linearen Funktionen an, welche Bedingungen für die
Parameter k und d jeweils gelten müssen (Füge ein: > , < , = )
g1:
k…0
d…0
g2:
k…0
d…0
g3:
k…0
d…0
g4:
k…0
d…0
b) Entscheiden Sie, welche der oben dargestellten Funktionen die nachfolgende reale
Situation abbildet und geben Sie die Bedeutung von k und d in diesem Zusammenhang an
Ein voller Tanklastwagen wird entladen.
Pro Sekunde wird immer dieselbe Menge an Öl abgelassen.
Möglicher Lösungsweg:
a)
g1: k > 0
d =0
g2: k = 0
d>0
g3: k < 0
d<0
g4: k < 0
d>0
b)
g4 bildet das ab, y = 200 – 0,5x
x…Zeit in Sekunden, 200 Liter sind im Wagen
in einer Sekunde wird 0,5 Liter abgelassen
y = verbleibendes Öl im Wagen
10
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3A,B,C,D Geschwindigkeit
Bei gleich bleibender Geschwindigkeit kann der zurückgelegte Weg berechnet werden mit
der Formel: Weg = Geschwindigkeit mal Zeit  s = v . t
a) Erstellen Sie ein Zeit-Weg-Diagramm für eine Geschwindigkeit von 50 km/h und von
75 km/h. Wie beeinflusst die Geschwindigkeit das Bild der Funktion?
b) Wie verändert sich der zurückgelegte Weg, wenn die Geschwindigkeit sich verdoppelt?
O Er bleibt gleich
O Er wird verdoppelt
O Er wird halbiert
O Er wird größer
c) Jemand möchte in derselben Zeit die dreifache Wegstrecke zurücklegen. Wie muss er die
Geschwindigkeit wählen?
d) Frau Matis benötigt für die tägliche Fahrt zur Arbeit (70 km) 50 Minuten. Sie fährt eines
Tages 5 Minuten später weg. Wie viel schneller als sonst muss sie fahren, wenn sie zur
gleichen Zeit ankommen möchte wie sonst auch?
Möglicher Lösungsweg:
a)
Der Anstieg der Geraden gibt die Geschwindigkeit wieder, daher ist s2 steiler, k = 75!
b) Er wird verdoppelt.
c) Er muss 3 mal schneller sein. v2 = 3. v1
d) Durchschnittlich um 9,33 km/h schneller.
IV 3A,B Farbe
Eine Malerfirma verlangt für das Mischen der Farbe für eine Hausfassade eine Grundgebühr
von 35 €, die Kosten für jeweils ein Liter Farbe betragen 1,50 €.
Geben Sie eine Gleichung für die Gesamtkosten an, wenn a Liter Farbe benötigt werden!
Möglicher Lösungsweg:
y = 1,5 a + 35
y = Kosten
a= Farbmenge in Liter
11
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV, 3A,C,D Ein Tag im Leben einer Wühlmaus
Skizze der Höhle:
…. Erdoberfläche
….“Vorratsebene“
….“Wohnebene“
….“Schlafebene“
Geschichte:
Nachdem die Wühlmaus wie jeden Tag pünktlich um 6°° morgens aufgewacht war, ging sie sofort in
die Vorratskammer, um etwas Essbares zu holen. Da sie noch müde war und vom gestrigen Laufduell
mit dem Eichhörnchen einen Muskelkater hatte, brauchte sie eine halbe Stunde, um nach oben in
den Vorratsraum zu kommen. Es war jeden Tag das gleiche: Oben angekommen konnte sich die
Maus eine Stunde lang nicht entscheiden, was sie nun zum Essen mit nach unten nehmen sollte. Sie
entschied sich dann wieder für eine der Nüsse, die sie unter dem Baum auf der Erdoberfläche
gefunden hatte. Schnell verschwand sie damit ins Wohnzimmer. Volle zwei Stunden spielte die
Maus mit der Nuss, um sie dann genüsslich zu essen.
Plötzlich hörte sie von oben ein Geräusch….
a) Versuchen Sie, die Position der Maus in der obigen Geschichte grafisch im vorgegebenen
Koordinatensystem darzustellen. Ordnen Sie dabei der jeweiligen Uhrzeit (x – Achse) die
Position der Maus zu! (Achtung: negatives Vorzeichen unter der Erdoberfläche!) Vergleichen
Sie die Zeichnung mit Ihrem Nachbarn und diskutieren Sie über Unterschiede.
….Erdoberfläche
12
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
b) Denken Sie sich eine Fortsetzung der begonnenen Geschichte aus und zeichnen Sie
den Graphen bis 18°° (natürlich 18°° im Tagesablauf der Maus) fertig!
c) Zeichnen Sie eine neue Höhle oder einen beliebigen Lebensraum eines Tieres und
stellen Sie den Ablauf einer anderen Zeitspanne, z.B. eine Stunde, eine Minute,…..
dar! Versuchen Sie hierfür selbst ein geeignetes Koordinatensystem zu erstellen.
d) Erklären Sie auf Basis der Definition von Funktionen, warum es sich bei dieser
Zuordnung um einen funktionalen Zusammenhang handelt!
e) Geben Sie die Definitionsmenge und die Wertemenge der dargestellten Funktionen
an!
f) Beantworten Sie folgende Fragen / Stimmen folgende Aussagen?
 Warum bildet hier eine durchgehende Linie den Funktionsgrafen?
 Uhrzeiten, zu denen sich die Maus auf der Wohnebene befindet werden gleiche
Funktionswerte zugeordnet! Warum kann man aus der Steigung des Funktionsgrafen
etwas über die Geschwindigkeit der Maus aussagen?
Sehr offene Aufgabe keine Lösung
IV 3A,B,C,D Zugverbindungen
Aufstellung der Züge, die zwischen 7:00 Uhr und 8:00 Uhr zwischen Wels und Linz verkehren.
(Stand März 2010)
Wels
Marchtrenk
Oftering
Hörsching
Pasching
Leonding
Linz
7:06 A
7:10-7:11
7:22
7:11 B
7:15-7:16
7:28
7:19 C
7:24-7:25
7:28-7:29
7:32-7:33
7:34-7:35
7:39-7:40
7:44
7:27 D
7:37-7:38
7:43-7:44
7:48
7:35 E
7:48-7:49
7:53
Linz
Leonding
Pasching
Hörsching
Oftering
Marchtrenk
Wels
7:13 F
7:13
7:27
7:28 G
7:28
7:40
a) Wie viele Möglichkeiten gibt es zwischen 7:00 Uhr und 8:00 Uhr von Wels nach Linz zu fahren?
Wie viele sind es von Linz nach Wels?
b) Mit welcher Durchschnittsgeschwindigkeit fährt A? Achten Sie auf die Einheiten und geben Sie
die Geschwindigkeit in m/s an. (v = s / t)
c) Mit welcher Durchschnittsgeschwindigkeit fährt E? Achten Sie auf die Einheiten und geben Sie
die Geschwindigkeit in km/h an.
d) Wie lange braucht C für die Strecke von Leonding nach Linz? Wie lange D?
e) Geben Sie beim Zug C die Koordinaten des Startpunkts und des Zielpunkts an, mit folgenden
Einheiten (1min/ 1km). Linz hat die Koordinaten (0/0). Erstellen Sie eine Geradengleichung, die
durch diese Punkte geht.
f) Geben Sie beim Zug G die Koordinaten des Startpunkts und des Zielpunkts an. Erstellen Sie eine
Geradengleichung, die durch diese Punkte geht.
g) Berechnen Sie den Schnittpunkt der beiden Geraden C und G= Treffpunkt der Züge.
h) Ist die Gerade steigend fährt der Zug von _________ nach __________.
i) Je steiler die Gerade ist, desto ____________ fährt der Zug.
Wels – Marchtrenk: 7km, Wels – Oftering: 12km, Wels – Hörsching: 15km,
Wels – Pasching: 17km, Wels – Leonding: 21 km, Wels – Linz: 25km
13
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
Möglicher Lösungsweg:
a)
b)
c)
d)
e)
f)
g)
5, 2
25 000: (16. 60) = 26,04 m/s
4:(4:60) = 60 km/h
C braucht 4 Minuten, D auch 4 Minuten
C: Startpunkt (25/25) Ziel (44/0),
G: Start (28/0) Ziel (40/25)
C: y = (-25x + 1100) / 19 D: y = (25x-700)/12 Schnitt: 34,19/12,9
Treffpunkt: 34,19-25 = 9,19 Minuten nach dem Start von C, 12,9 km von Linz entfernt zwischen
Hörsching und Oftering, knapp vor Oftering.
h) Ist die Gerade steigend fährt der Zug von Linz nach Wels.
i) Je steiler die Gerade ist, desto schneller fährt der Zug.
IV 3A,C Diesel
Ein Auto verbraucht auf jedem Autobahnkilometer a Liter Diesel, ansonsten pro km b Liter.
Ein Liter Diesel kostet p €.
Auf einer Fahrt werden x km auf der Autobahn und y km auf sonstigen Straßen (in der Stadt,
Landstraßen, etc.) gefahren.
a) Geben Sie in Worten an, was mit dem Term ax + by berechnet wird.
b) Geben Sie einen Term an, mit dem die Kosten für die Gesamtstrecke berechnet werden
kann.
Möglicher Lösungsweg:
a) ax + by gibt den Gesamtverbrauch in Liter auf x km Autobahn und y km Landstraße an.
b) Kosten= p(ax + by)
14
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3-A,B,C,D Rolltreppen
Rolltreppen bewegen sich in Österreich in Flughäfen mit 2,34 km/h, in Kaufhäusern mit 1,8 km/h.
In Asien wird generell mit 2,7 km/h gefahren, damit mehr Menschen transportiert werden können.
Mit Höchsttempo, fast 2,8 km/h, fahren die Treppen der Moskauer Metro.
Die nach t Minuten zurückgelegten Strecken s(t) in Meter werden durch folgende Gleichungen
angegeben:
2340
t
60
1800
sKaufhaus 
t
60
2700
s Asien 
t
60
2800
sMoskau 
t
60
sFlughafen 
a) Berechnen Sie für alle vier Funktionen die Dauer für eine Strecke von 100m.
Geben Sie die Zeitunterschiede in Sekunden und die prozentuellen Zeitunterschiede bezogen auf die kürzeste Zeit - an und stellen Sie die Ergebnisse in einer Tabelle dar.
b) Formulieren Sie vergleichende Antwortsätze in der Form „Während eine Rolltreppe in einem
Flughafen für 100m…“
c) Formulieren Sie Antworten zu:
i) sFlughafen(10) = ? und
ii) sFlughafen (t=?) = 200
d) Ordnen Sie den nachstehenden Graphen die Funktionsgleichungen zu.
15
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
Möglicher Lösungsweg:
a)
Flughafen: 100 = 39t
Kaufhaus: 100 = 30t
Asien: 100 = 45t
Moskau: 100 = 46, t
t = 2,56 min = 153,85 Sekunden
t =3, min = 200 Sekunden
t = 2, min = 133, Sekunden
t = 2,14 min = 128,57 Sekunden...kürzeste Zeit
Dauer für 100m absoluter Unterschied
in Minuten
in Sekunden
Flughafen-Rolltreppe
2,56
25,27
3,
Kaufhaus-Rolltreppe
71,43
2,
Rolltreppe in Asien
4,76
Rolltreppe in
Moskau
2,14
relativer Unterschied
in Prozent
19,
55,56
3,7
b)
Während die Rolltreppe in einem Flughafen für 100m 2 Minuten 33,85 Sekunden braucht,
braucht sie für diese Strecke in einem Kaufhaus 3 Minuten 20 Sekunden, in Asien 2 Minuten
13, Sekunden, in der Moskauer Metro nur 2 Minuten 8,57 Sekunden.
Die Rolltreppe in der Moskauer Metro ist somit 25,27 Sekunden schneller als in einem
Flughafen, 1 Minuten 11,43 Sekunden schneller als in einem Kaufhaus und 4,76 Sekunden
schneller als in Asien.
In Moskau ist die Rolltreppe somit um 19, % schneller als in einem Flughafen, 55,56 %
schneller als in einem Kaufhaus und um 3,7 % schneller als in Asien.
c) sFlufhafen(10) = 39·10 = 390 m
sFlughafen (t) = 200
200 = 39t
t = 5,13 min
In einem Flughafen fährt die Rolltreppe in einer Zeit von 10 Minuten eine Strecke von
390 m, für 200m braucht die Rolltreppe 5,13 Minuten.
d)
Reihenfolge von oben nach unten:
oberste: Moskau
Asien
Flughafen
unterste: Kaufhaus
16
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3-A,B,C Internetzugang
Die monatliche Grundgebühr eines Internetzuganges bei Anbieter A beträgt 12 Euro. Eine
Sekunde Online-Zeit kostet 0,00035 Cent.
a) Stellen Sie die Funktionsgleichung f der Kosten, abhängig von der Online-Zeit auf.
Begründen Sie das Ansteigen der Geraden.
b) Berechnen Sie die Gesamtkosten für 17,5h Onlinezeit!
c) Berechnen Sie, wie lange man für 50 Euro online sein kann!
Möglicher Lösungsweg:
a.) Die vorgegebene Größe ist die Zeit; Einheit Minuten.
Die abhängige Größe sind die Kosten K in Euro, die eine Funktion der Zeit t sind:
K = f(t) = 0,021t + 12
b.) 17,5 h = 17,5·60 = 1050 min. Gesucht sind die Kosten für 1050 min, also f(1050):
f(1050) = 0,021·1050 + 12 = 34,05 Euro.
c.)Gesucht ist dasjenige t, für das die Kosten f(t)=50 Euro betragen:
f(t) = 0,021t + 12 = 50  t = 30h 9min 31s
IV 3-A,C Produktion
2500
Herstellungskosten / €
2400
2300
Was lässt sich alles
aus dem Diagramm ablesen?
2200
2100
2000
1900
1800
1700
1600
1500
0
100
200
300
400
500
600
Produktionsmenge / Stück
Möglicher Lösungsweg:
Es gibt zwischen den Herstellungskosten und der Produktionsmenge einen linearen
Zusammenhang, je mehr produziert wird, desto mehr stiegen die Kosten.
pro 100 Stück um 125 €. Die Fixkosten betragen 1600 €.
Die Funktionsgleichung mit x…Produktionsmenge, y …Herstellungskosten y = 1,25 x + 1600
17