Gleichungen und Ungleichungen

Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
Gleichungen und Ungleichungen
Gleichungen
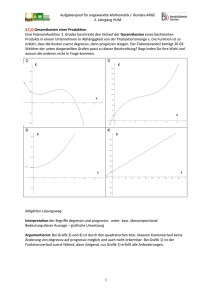
III 2-A Gleichung suchen
Wie lautet eine lineare Gleichung, deren Definitionsmenge die Zahl 3 nicht enthält und deren
Grundmenge Q ist?
Möglicher Lösungsweg:
Es gibt unendlich viele Möglichkeiten für eine solche gesuchte Gleichung mit D = Q \{3}
zB:
2x
3
x3

 1 uam
oder
x 3 5
2x  6
III 2-B,D Was ist falsch?
Begründen Sie, ob und warum hier richtig/falsch gerechnet wurde:
7x – 5 = 5+ 7x | +5 – 7x
x = 10
Stellen Sie gegebenenfalls richtig!
Möglicher Lösungsweg:
Durch die Umformung mit +5 - 7x erhält man:
0 = 10 (nicht x = 10), da das eine falsche Aussage ergibt, hat die angegebene Gleichung keine
Lösung.
III 2-C,D Gleichungsüberprüfung
Prüfen Sie die Äquivalenzumformungen bei der folgenden Gleichung.
x x
x    10 |∙6
2 3
6x – 3x – 2x = 10
x = 10
a) Stellen Sie Fehler richtig!
b) Geben Sie Überprüfungsmöglichkeiten für die Lösung an!
c) Geben Sie eine Lösungsmenge in der Grundmenge Z an!
d) Erfinden Sie einen passenden Text zur Gleichung!
1
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
Möglicher Lösungsweg:
a) 1. Zeile: Rechte Seite wurde nicht mit 6 multipliziert, richtige Lösung x = 60.
b) Überprüfungsmöglichkeiten: Solver mit Technologie, Einsetzen der Lösung in die erste
Zeile muss zu einer wahren Aussage führen.
c) L = {60}
d) Meine Schwester hat von ihrem Taschengeld zuerst die Hälfte für ein T-Shirt und dann ein
Drittel für ein Buch ausgegeben und hat jetzt nur mehr 10 € übrig. Wie viel Taschengeld
hatte sie ursprünglich.
III 2-A,B D Zuordnungen
Das um 7 vermehrte Dreifache einer Zahl ist gleich dem um 9 verminderten Vierfachen
derselben Zahle. Wie heißt sie?“
a. Übersetze in die Sprache der Mathematik:
Text
Um 7 vermehrt
Dreifache einer Zahl
Um 9 vermindert
Vierfache einer Zahl
Mathematik
b. Welche der folgenden Gleichungen entspricht dem oben genannten Text
 3.x-9=4.x-7
 7.x+3=9.x-4
 3.x+7=4.x-9
 3.x+7=4.x+9
 7.(3+x)=9.(x-4)
Möglicher Lösungsweg:
Text
Um 7 vermehrt
Dreifache einer Zahl
Um 9 vermindert
Vierfache einer Zahl
Mathematik
+7
3 .x
-9
4 .x
c. Welche der folgenden Gleichungen entspricht dem oben genannten Text
 3.x-9=4.x-7
 7.x+3=9.x-4
2
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
o 3 . x+7=4.x-9
 3.x+7=4.x+9
 7.(3+x)=9.(x-4)
III 2-B -Monatslohn
Ein Fünftel des Monatslohns wird benötigt um die Energieversorgung des Hauses zu
finanzieren, rund ein Drittel machen die Lebenshaltungskosten der Familie aus, ein Viertel
sind sonstige regelmäßige Ausgaben. Es bleiben 1040 Euro auf dem Konto übrig. Wie hoch
war der Monatslohn?
Möglicher Lösungsweg:
Lohn ....x
x - x/5 - x/4 - x/3 = 1040 Gleichung auflösen
13x/60 = 1040
x = 4 800 Euro beträgt der Monatslohn
III 2-A – Waldorfsalat
In der Küche sollen Äpfel, Nüsse und Sellerie in kleine Stücke geschnitten, als Basis für den
Waldorfsalat vorbereitet werden.
Die Apfelmasse muss doppelt so schwer sein wie die Selleriemasse und die Walnüsse dürfen
nur ein Viertel der Selleriemasse wiegen.
Sellerie kostet pro kg € 1,Äpfel kosten pro kg € 1,50
Walnüsse kosten pro kg € 4,a) Welche exakten Mengen werden von den 3 Grundstoffen benötigt, wenn 5 kg
Rohmasse für Waldorfsalat hergestellt werden soll?
b) Wie viel kosten 5 kg dieser Rohmasse?
Möglicher Lösungsweg:
Bestandteil
Sellerie
Äpfel
Walnüsse
Summe
Masse in kg
x
2x
x/4
13x/4
Sellerie: 1,54 kg
Äpfel:
3,08 kg
Walnüsse: 0,38 kg
Summe:
5 kg
7,70 €
Preis
x
3x (=2x . 1,5)
x (=x/4 . 4)
5x
13
x5
4
Preis: 1,54 €
Preis: 4,62 €
Preis: 1,54 €
3
13x  20
x
20
13
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
III 2-B-Preisgeld
Ein Preisgeld von 76 000 Euro soll unter drei Preisträgern so aufgeteilt werden, dass jeder
1/3 weniger bekommt als der Vorgänger. Wie viel bekommt jeder?
Möglicher Lösungsweg:
1. bekommt x, 2. bekommt x-x/3 = 2x/3
Der Dritte bekommt 2x/3 - 2x/9 = 4x/9
x + 2x/3 + 4x/9 = 19x/9 = 76 000
x = 36 000
1: 36 000
2: 24 000 3: 16 000 Euro
III 2-A, B C Gewinn
Der Gewinn einer OHG ist laut Gesellschaftsvertrag wie folgt auf die Gesellschafter Müller,
Paier, Schmidt aufzuteilen. Paier enthält 4/5 des Gewinnanteils von Müller, Schmidt enthält
3/4 des Gewinnanteils von Paier. Wie viel erhält jeder, wenn der Gewinn €600 000 beträgt?
Möglicher Lösungsweg:
Müller bekommt m, Paier bekommt 4m/5, Schmidt bekommt ¾(4m/5) = 3m/5
m + 4m/5 + 3m/5 = 600 000  m =Müller: 250 000€, Paier: 200 000€, Schmidt: 150 000€
III 2-A,B Suezkanal
Beim Bau des Suezkanals waren 13/20 seiner Länge natürliche Wasserwege, die nur
vertieft werden mussten, 1/ 4 der Gesamtlänge musste ausgesprengt werden, der Rest von
16,4 km waren brauchbare Wasserstraßen. Die Sprengungskosten betrugen 1 Mio. $ pro
km. Die Kosten der Vertiefung betrugen 1/3 der Sprengungskosten pro km.
a) Stellen Sie die Situation in einer Gleichung dar!
b) Berechnen Sie die Länge des Suezkanals!
c) Wie hoch sind die Sprengungskosten, wie hoch die Vertiefungskosten?
Möglicher Lösungsweg:
13
x
x   16,4  x x…Länge des Kanals
a)
20
4
b) Länge : x = 164 km
c) Sprengungskosten: 106  41 = 41.000.000 $
106
 106,6  35.533.333,33 $ = 3,55 . 107 $
Vertiefungskosten:
3
III 2-A, B, C Studenten-WG
Eine Wohnung hat 120m². Drei Studenten wollen eine WG gründen. Zimmer A hat 30m²,
Zimmer B hat 25 m² und Zimmer C hat 20 m². Der Rest ist Gemeinschaftsbereich
(Wohnzimmer, Bad…)
Die Gesamtmiete für die Wohnung beträgt 1050 €.
Wie sollten die drei Studenten die Miete fair aufteilen?
4
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
Möglicher Lösungsweg:
Gemeinschaftsbereich: 45m², Student 1 verwendet 75m²
Student 2 verwendet 70m², Student 3 verwendet 65m²
Aufgabe : teile 1050 im Verhältnis 75:70:65
75k+70k+65k=1050
210k=1050
k=5
5 . 75 = 375€, 5 . 70 = 350€ 5 . 65 = 325€
Student 1 bezahlt 375€, Student 2 bezahlt 350€, Student 3 bezahlt 325€.
III 2-A,D Schülerzeitung
2 Schüler arbeiten an einer Schülerzeitung. Thomas investiert ca. 60 Stunden und Markus
40 Stunden Zeitaufwand. Einen Gewinn von € 120,- wollen sie entsprechend ihrer
Arbeitsanteile aufteilen.
a) Markus fordert € 54,- des Gewinns. Thomas erhält den Rest. Beurteilen Sie, ob diese
Aufteilung gerecht ist!
b) Überprüfen Sie, welche der folgenden Aussagen der ursprünglichen Abmachung
entsprechen und begründen Sie Ihre Entscheidung.

Thomas und Markus teilen den Gewinn im Verhältnis 3 : 2.

Markus leistet 40 % der Arbeit.

Thomas bekommt zwei Drittel des Gewinns.
c) Thomas präsentiert seinem Partner folgende Berechnung seines Gewinnanteils. Hat
er richtig gerechnet? Wenn nicht, finden Sie den Fehler!
0,66 . 120 = 79,29 €
Möglicher Lösungsweg:
a) Nein, denn richtige Aufteilung wäre:
Lösung mittels Proportionalitätsfaktor t: Markus 40 t, Thomas 60 t
60 t + 40 t = 120
100t = 120
t = 1,2
Markus: 40 . 1,2 = 48 €
b)

3 : 2 ist korrekt, da 60 : 40 = 3 : 2

Gesamtarbeitszeit beträgt 100 h, das entspricht 100 %, also sind 40 h 40 %
60 3
 .

Falsch! Der Anteil von Thomas ist
100 5
c) Falsch! Sein Anteil ist 60 % von 120 € = 0,6 . 120 = 72 €
5
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
Formeln
III 2-B,C,D
Größen in Formeln schätzen
b 1
1
ax
Wie ändert sich der Wert des Bruchs, wenn a größer wird? b, x bleiben gleich.
Wie ändert sich der Wert des Bruchs, wenn x kleiner wird? a,b bleiben gleich.
Wie groß wird der Wert des Bruchs, wenn x verdoppelt wird? a, b bleiben gleich
Formen Sie die Formel nach x um!
Berechnen Sie den Wert von a, wenn x=7 und b=34 ist.
Für welche Werte von a,b oder x wird diese Gleichung zu einer falschen Aussage.
Gegeben ist die Formel
a)
b)
c)
d)
e)
f)
Möglicher Lösungsweg:
a) Wert wird kleiner als 1
b) Wert wird größer als 1
b1
d) x 
a
f) Es gibt hier viele Möglichkeiten. Bsp: a = 1, b= 1, x= 1
c) 0,5
e) a = 5
III 2-A, C, D Rechteck
Die Formel zur Berechnung des Flächeninhalts eines Rechtecks A = a. b ist bekannt.
Gehen Sie davon aus, dass der Flächeninhalt konstant ist.
Wie verändert sich Länge der Seite a, wenn sich die Länge der Seite b verdoppelt (halbiert)?
Begründen Sie Ihre Aussage.
Lösung:
A = a  b | :b
A
b
Wenn sich die Länge der Seite b verdoppelt, halbiert sich die Länge der Seite a.
Wenn sich die Länge der Seite b halbiert, verdoppelt sich die Länge der Seite a.
Je größer die Länge der Seite b wird, um so kleiner wird die Länge der Seite a und umgekehrt
a=
6
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
Ungleichungen
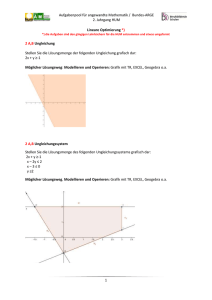
III 2-B,D Was ist falsch?
Die Lösung einer Ungleichung:
2  x 2x
x

|3
3
3
3x  2  x  2x | 4x
2  2x
1x
|: (2)
L  1,  
Finden Sie den Fehler und erklären Sie, wie es richtig ist.
Stellen Sie die richtige Lösungsmenge grafisch dar.
Möglicher Lösungsweg:
3. Zeile: Die Division durch die negative Zahl bewirkt eine Änderung des Relationszeichens.
Ab 4. Zeile richtig:
1x
x 1
L
  ,1
III 2-A,B,C,D Tulpenzwiebeln
Sie möchten original holländische Tulpen anpflanzen. Bei einem Onlinehändler werden Sie
fündig. Eine Zwiebel der Sorte „Rosa“ kostet € 0,75. Für den Versand werden zusätzlich
einmal € 5,- verrechnet. Sie haben € 16,- zur Verfügung.
a) Stellen Sie eine Formel auf, mit der Sie den Rechnungsbetrag B darstellen können, wenn
Sie x Tulpenzwiebeln der Sorte „Rosa“ kaufen.
b) Wie viele Zwiebeln der Sorte „Rosa“ können Sie bestellen? Wie viel Geld bleibt Ihnen?
Möglicher Lösungsweg:
a) B = 0,75x + 5
b) 0,75x + 5 ≤ 16
x ≤ 14,67
Man kann 14 Zwiebeln kaufen. Es bleiben 11- 0,75 . 14 = 0,5 50 Cent übrig
7