Aufgaben3 - schule.at

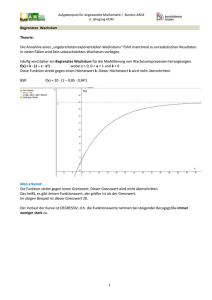
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
Funktionen-Teil3
IV 3A,B,C Bergsteigen
Ein Bergsteiger steigt vom Arthurhaus zum Gipfel des Hochkönig auf. Nach einer Stunde
erreicht er eine Seehöhe von 1786 m. Nach 3 Stunden befindet er sich auf 2346 m Seehöhe.
a) Stellen Sie als Modell eine lineare Funktion auf, die den Zusammenhang der Dauer des
Bergsteigens mit der erreichten Seehöhe angibt. Was bedeuten k und d in diesem
Beispiel? (Ist dieses Modell realistisch?)
b) Zeichnen Sie den Graphen dieser Funktion in einem sinnvollen Bereich.
c) In welcher Seehöhe wird sich der Bergsteiger nach 4¾ Stunden Gehzeit befinden?
d) Nach wie vielen Stunden wird er den Gipfel des Hochkönig in 2941 m Seehöhe
erreichen?
e) Auf welcher Seehöhe befindet sich das Arthurhaus als Ausgangspunkt dieser
Wanderung?
f) Der Abstieg vom Gipfel erfolgt in 4,1 Stunden. Wie lautet nun k für eine lineare
Funktion, die diesen Abstieg beschreibt?
g) Ermitteln Sie auch d und zeichne den Graphen der Funktion.
Möglicher Lösungsweg:
a) f(x) = 280x + 1506;
k….zurückgelegter Höhenunterschied pro Stunde,
d….Ausgangshöhe
gerade diese Bergtour ist völlig unpassend für ein lineares Modell des zurückgelegten
Höhenunterschieds. Auf der Wanderung vom Arthurhaus zum Gipfel des Hochkönig legt man
zwar relativ die 1435 Höhenmeter zurück, absolut sind es aber viel mehr (ca. 2000m), da die
Wanderroute auch viele Abstiege hat.
b)
c)
d)
e)
f)
g)
–siehe Graph f
2836 m
5,125 Stunden
1506 m
-350
2941 siehe Graph g
1
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3-A,D Bergtour
Ein Wanderer macht eine Bergtour. Er startet in Punkt A und will zu Punkt B. Die Karte ist im
Maßstab 1:10000.
Quelle: austrianmap.at
a) Wie groß ist die Entfernung (Luftlinie)?
b) Welche Höhendifferenz muss er überwinden?
c) Wie groß ist der durchschnittliche Anstieg in %?
Möglicher Lösungsweg:
a) 6cm 60 000 cm = 600 m
b)
49 m
c) k = 49/600 = 0,0482 = 4,82%
IV 3 A,B Preisnachlass
Herr Wagner weiß, dass beim Hausbauen in erster Linie die Preisnachlässe verglichen
werden. Er möchte ein bestimmtes Fenster um € 100,- verkaufen. Darum rechnet er vor
dem Verkauf 30 % dazu ( = Listenpreis), um dann 30 % Nachlass gewähren zu können.
a)
Begründen Sie, ob seine Überlegung richtig oder falsch ist !
b)
Welchen Preis muss er vor dem Verkauf angeben, damit er bei 20 % Preisnachlass
auf € 100,- kommt ?
c)
Geben Sie eine allgemeine Formel an, mit der man den Listenpreis L berechnen
kann, um nach einem Preisnachlass von x % auf den Verkaufspreis P zu kommen !
Möglicher Lösungsweg:
a)
Die Überlegung ist falsch, da 30 % von € 100,- einen anderen Wert ergeben als 30 %
vom höheren Preis. Er müsste € 142,86 verlangen.
b)
80 % ………. € 100,100 % ……….
L
L = 100. 100/80 = 125
Listenpreis: € 125,c)
(100 – x) % ………. P
100 %
………. L
L = 100 P : (100-x)
2
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV A,B,C,D Preis und Nachfrage
Die Höhe des Preises (p) einer Ware und der Umfang der Nachfrage (n) können bei Vernachlässigung
anderer Markbedingungen, in einer sogenannten Nachfragefunktion n = ap+b dargestellt werden.
a) Welches dieser Diagramme bildet die Nachfragefunktion realistisch ab?
b) Kann die Nachfrage n dann auch negative Werte annehmen?
c)Geben Sie eine mathematisch sinnvolle Definitionsmenge für dieses Beispiel an!
d) In unserem Beispiel ergibt sich die Nachfrage aus dem Preis. Wandeln Sie die vorgegebene
Gleichung um, so dass sich der Preis aus der Nachfrage ergibt. Lösen Sie die Aufgabenstellung sowohl
rechnerisch als auch grafisch!
e) Erklären Sie die Bedeutung der Variablen a und b!
Möglicher Lösungsweg:
a) Diagramm 2, mit steigendem Preis sinkt die Nachfrage)
b)Nein
c) R+;R0+
d)
grafisch:
e) a gibt an, wie schnell die Nachfrage bei steigendem Preis
Spiegelung
an
der
sinkt. b wäre (weil realitätsfremd) die Nachfrage bei Preis €
nb
p
ersten Mediane
0,-!
a
1 b
p  n
a a
IV 3-A,B Christkindlmarkt
Ein Reiseanbieter stellt fest, dass die dreitägige Fahrt zum Christkindlmarkt nach Nürnberg
bei einem Preis von € 179,- von 120 Gästen gebucht wird. Bei einer Preissenkung auf € 159,kann der Verkauf der Reise auf 150 Gäste gesteigert werden.
a) Welche Funktion erklärt den zu erwartenden Erlös?
b) Kann durch die Preissenkung der Erlös erhöht werden?
c) Ist die prozentuelle Änderung der Nachfrage größer als die prozentuelle Änderung des
Preises, so spricht man von einer elastischen Nachfrage.
Ist die Nachfrage für diese Preissenkung elastisch?
Möglicher Lösungsweg
a) E(x) = p . x b) E1(x) = 179 . 120 = 21480 und E2(x) = 159 . 150 = 23850
Der Erlös erhöht sich durch Preissenkung und der daraus resultierenden gestiegenen
Nachfrage deutlich!
c)
Prozentuelle Änderung der Nachfrage: 150/120 = 1,25 à 25% Steigerung
Prozentuelle Änderung des Preises: 159/179 = 0,888268.. à 11,2% Abnahme
3
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3-D- Point of no return
Ein Flugzeug fliegt mit der Durchschnittsgeschwindigkeit v=300 km/h, der Treibstoff reicht
für 2 Stunden.
a)
Bei Windstille fliegt das Flugzeug also 1 Stunde 300 km weit, kehrt um und landet nach
einer weiteren Stunde wieder am Startpunkt.
b) Das Flugzeug fliegt den ersten Abschnitt der Flugroute mit Gegenwind
(Windgeschwindigkeit w=100 km/h), kehrt nach 300 km um und fliegt mit Rückenwind
(Windgeschwindigkeit w=100 km/h) wieder zurück. Es erreicht nur leider den Startpunkt
nicht mehr.
c) Das Flugzeug fliegt den ersten Abschnitt der Flugroute mit Rückenwind
(Windgeschwindigkeit w=100 km/h), kehrt nach 300 km um und fliegt mit Gegenwind
(Windgeschwindigkeit w=100 km/h) wieder zurück. Es erreicht nur leider den Startpunkt
nicht mehr.
Ordnen Sie dem jeweiligen Sachverhalt eine graphische Darstellung zu und begründen Sie
Ihre Entscheidung.
Darstellung A
Darstellung B
Darstellung C
Darstellung D
Darstellung E
Möglicher Lösungsweg:
Schlüsselwörter in der Argumentation: Geradensteigung entspricht Geschwindigkeit, kein
linearer Zusammenhang zwischen Steigungswinkel und Geschwindigkeit, parallele Geraden
entsprechen gleichen Geschwindigkeiten, Bewegungsgleichungen, Rücken- und Gegenwind
sind (nicht) austauschbar
4
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3-D- Point of no return. ein wenig anders
Ein Flugzeug fliegt mit der Durchschnittsgeschwindigkeit v=300 km/h, der Treibstoff reicht
für 2 Stunden.
Bei Windstille fliegt das Flugzeug also 1 Stunde 300 km weit, kehrt um und landet nach einer
weiteren Stunde wieder am Startpunkt.
Betrachten Sie nun zwei Szenarien, wobei w = Windgeschwindigkeit.
a) Das Flugzeug fliegt den ersten Abschnitt der Flugroute mit Gegenwind ( w=100 km/h),
kehrt nach 300 km um und fliegt mit Rückenwind (w=100 km/h) wieder zurück. Es erreicht
nur leider den Startpunkt nicht mehr.
b) Das Flugzeug fliegt den ersten Abschnitt der Flugroute mit Rückenwind (Geschwindigkeit
w=100 km/h), kehrt nach 300 km um und fliegt mit Gegenwind (Geschwindigkeit w=100
km/h) wieder zurück. Es erreicht nur leider den Startpunkt nicht mehr.
Erläutern Sie, warum das Flugzeug nicht mehr zurückkehren kann.
Argumentieren Sie mit Hilfe einer Grafik gegen die Einwände eines Skeptikers: „Ob zuerst
Rückenwind oder zuerst Gegenwind herrscht, müsste egal sein.“ – „Mit Rückenwind bin ich
doch schneller und brauche weniger Treibstoff.“ – „Den Treibstoff, den ich bei Gegenwind
mehr verbrauche, spare ich bei Rückenwind.“
Wo müsste das Flugzeug umkehren, damit es nach 2 Stunden gerade noch zum Startpunkt
zurückkehren kann?
Verwenden Sie für die Argumentation die folgende Skizze.
Mögliche Lösungswege:
Schlüsselwörter in der Argumentation: Geradensteigung entspricht Geschwindigkeit, kein
linearer Zusammenhang zwischen Steigungswinkel und Geschwindigkeit, parallele Geraden
entsprechen gleichen Geschwindigkeiten, Bewegungsgleichungen, Rücken- und Gegenwind
sind (nicht) austauschbar
5
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
Hinflug mit Rückenwind, Rückflug mit Gegenwind
Hinflug mit Gegenwind, Rückflug mit Rückenwind
Umkehrpunkt bei Hinflug mit Rückenwind und Rückflug mit Gegenwind
Umkehrpunkt bei Hinflug mit Gegenwind und Rückflug mit Rückenwind
6
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3-A,C,D Text erfinden
Betrachten Sie folgende Diagramme!
a) Überlegen Sie zu jedem Diagramm eine passende Problemstellung aus dem alltäglichen
Leben und formulieren Sie je ein Textbeispiel.
b) Ergänzen Sie die Diagramme mit den für Ihre Texte entsprechenden Achsenbeschriftungen.
c) Gibt es ein Zahlenpaar, welches in beiden Diagrammen vorkommt?
d) Können Sie Fragestellung c auf Ihre Beispiele sinnvoll anwenden? Begründen Sie!
e) Nennen Sie je eine Funktionsgleichung, welche diese Zahlenpaare beinhaltet.
Diagramm 1:
Diagramm 2:
7
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
Mögliche Lösungswege:
a.)Diagramm 1)
Samuel geht ins Schwimmbad. Der Eintritt kostet 2 €. Weiters möchte er sich Süßigkeiten
kaufen, welche jeweils 25 Cent kosten. Erstelle eine Kostenfunktion für Samuels
Schwimmbadaufenthalt.
Diagramm 2)
Emilia geht in ein Geschäft und kauft Schokolade. Eine Tafel kostet 0,5 €. Wie viel muss
Emilia bezahlen, wenn sie eine, zwei, drei,… Tafeln kauft? Erstelle eine Kostenfunktion.
b.) Achsenbeschriftung:
D1: 1. Achse: Anzahl Süßigkeiten
2. Achse: €
D2: 1. Achse: Anzahl Tafel Schokoladen 2. Achse: €
c.) Ja : ( 4/8)
d.) Ja kann ich, weil ich vergleichen kann, wie viel Geld von beiden ausgegeben wird.
e.)
Samuel: f(x) = 0,25 x + 2
Emilia : f(x) = 0,5 x
IV 3A,B, C,D Handyvertrag
Melanie möchte einen Handyvertrag abschließen. Sie überlegt, ob sie den Tarif Two oder
den Tarif Two Young wählen soll.
Preise in €
Grundgebühr /
Monat
Gespräch/Minute
Two
5,00
Two Young
10,00
0,20
0,10
a) Bei welcher monatlichen Gesprächszeit sind die beiden Tarife gleich? Stellen Sie den
Sachverhalt in einer Gleichung dar!
b) Stellen Sie den Graph in einem geeigneten Intervall dar!
c) Diskutieren Sie in welchem Bereich Two oder Two Young günstiger ist!
d) Sie sollen Ihre Freundin beraten: Sie wird pro Monat 40 Minuten (ohne Freiminuten)
telefonieren. Für welches Angebot soll sie sich entscheiden und wie groß ist ihre
Ersparnis? Dokumentieren Sie alle Rechenschritte!
Möglicher Lösungsweg:
a) 5 + 0,2 x = 10 + 0,1 x
x = 50
c) Unter 50 min ist Two günstiger.
Über 50 min ist Two Young günstiger
d) Für die Freundin ist Angebot Two um 1 €
günstiger.
8
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3-B,C Handytarife
Interpretieren Sie die folgende Grafik hinsichtlich:
a) Beschreiben Sie die Funktionen mittels einer Funktionsgleichung!
b) Welche der beiden Funktionen hat eine Grundgebühr? Wie viel?
c) Bei wie vielen Gesprächsminuten/Monat sind die Tarife gleichwertig?
d) Die Schülerin X telefoniert im Schnitt 170 min. pro Monat. Welcher Tarif kann ihr
empfohlen werden?
e) Der Schüler Y telefoniert im Schnitt nur 100 min. pro Monat. Welchen Tarif kann
man ihm empfehlen?
f) Bei wie vielen Gesprächsminuten/Monat ist Tarif A bzw. Tarif B günstiger?
g) Sind Handytarife generell als lineare Funktion darstellbar? (Tipp: Taktung)
Möglicher Lösungsweg:
Lösung
a) Tarif A: y = 0,05x + 10; Tarif B: y = 0,12x
b) Tarif A hat eine Grundgebühr von 10 Euro, erkennbar an d = 10.
c) 0,05x + 10 = 0,12x  x = 142,86
Die Tarife sind bei 142,86 Gesprächsminuten gleichwertig.
d) fA(170)=0,05.170 +10 = 18,5
fB(170 = 0,12 . 170 = 20,4
Für die Schülerin X wird Tarif A empfohlen.
e) fA(100) = 0,05 . 100 + 10 = 15
fB(100) = 0,12 . 100 = 12
Für den Schüler Y wird Tarif B empfohlen.
f) Erkennbar aus Aufgabe c! Bis 143 Minuten ist Tarif B günstiger, telefoniert man jedoch
mehr als 143 Minuten pro Monat, so sollte man Tarif A wählen.
g) Nein. Minuten werden in 1-Minuten-Taktung, bzw. in 0,5-Minuten-Taktung abgerechnet,
was einer Treppenfunktion entsprechen würde.
IV 3B,C,D Tarif nach Telefonierverhalten
Herr Muster möchte für sich, die Großmutter und seinen Sohn Sebastian neue Handys
9
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
besorgen. Erfahrungsgemäß telefoniert Sohn Sebastian durchschnittlich häufig. Der Vater
benutzt das Handy sowohl privat als auch beruflich sehr intensiv, während die Großmutter
ihr Handy nur im Notfall verwendet. Es drei verschiedene Telefontarife zur Auswahl:
(A) keine Grundgebühr; Gesprächsgebühr: 4,9 Cent pro Minute
(B) Grundgebühr: 9,90.- €; Gesprächsgebühr: 2,9 Cent pro Minute
(C) Grundgebühr: 19,90 €; Gesprächsgebühr: 1,9 Cent pro Minute
a) Welchen Tarif würden Sie spontan welcher Person zuordnen? Begründen Sie Ihre
Entscheidung.
b) Beschreiben Sie die einzelnen Tarife mit Hilfe einer Formel.
c) Der Vater beobachtet das Telefonierverhalten von Sebastian einen Monat lang und
stellt eine Gesprächsdauer von 10 Stunden fest. Berechnen Sie, welchen Tarif er für
seinen Sohn wählen soll!
d) Berechnen Sie, ab welcher monatlichen Gesprächsdauer der Tarif am günstigsten ist.
e) Stellen Sie den Verlauf der einzelnen Tarife graphisch dar.
Möglicher Lösungsweg:
a)A) Großmutter, sie telefoniert selten und kurz, daher wird sie relativ billig ohne
Grundgebühr wegkommen.
B) Sebastian telefoniert oft, kleine Grundgebühr und mittlere Kosten pro Minute
C) Vater, falls er mehr telefoniert als Sebastian und wahrscheinlich länger, dann ist die
teuerste Grundgebühr sinnvoll und die billigsten Minutentarife
b) x ... Minuten, f(x)... Kosten in €
c) f(600)=29,4 €
(A) f(x)=0,049x
g(600)=27.3 €
(B) g(x)=0,029x + 9,9
h(600)=31.3 €
(C) h(x)=0,019x + 19,9
d) Wann sind (B) und (C) gleichwertig: 0.029x + 9.9 = 0.019 x + 19.9
-> ab 1000 Minuten (Kosten: 38.9€) ist Tarif (C) günstiger.
e)
IV 3-A,D Richtiger Tarif
Welche Funktion beschreibt welchem Mobiltelefontarif? Ordnen Sie zu!
10
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
1
A Carina zahlt keine Grundgebühr und in
alle Netze dieselbe Gesprächsgebühr.
B Fabian hat eine Wertkarte von der der
Minutentarif abgezogen wird.
C Alex hat eine Flatrate. Egal wie viel er
telefoniert, er zahlt immer denselben
Fixbetrag.
D Sabine zahlt eine Grundgebühr und in
alle Netzen dieselbe Gesprächsgebühr.
2
3
4
Lösung: 1-D, 2-C, 3-A, 4-B
IV 3-A,BC E-Werk
Zwei Elektrizitätswerke A, B haben folgende Konditionen:
A: Grundgebühr G1 = 10.- €, Preis k1/kWh = 0,08 €
B: keine Grundgebühr, Preis k2/kWh = 0,4 € R…Rechnung
a) Stellen Sie eine Wertetabelle für RA und RB (0, 10, 20, 30, 40, 50 kWh) auf!
b) Stellen Sie Funktionsterme für RA und RB auf! (R = k . x + G)
c) Zeichnen Sie die Graphen der Rechnungsbeträge!
d) Was lässt sich aus der Zeichnung ablesen?
e) Bei welchem Verbrauch sind die monatlichen Gesamtkosten gleich?
f) Wie hoch sind die Kosten im Fall e)
Gruppenbildung: Jede Gruppe teilt sich in Befürworter und Gegner des grafischen Lösens!
Schreiben Sie jeweils die besten Argumente auf!
Möglicher Lösungsweg:
a)
0
10
20
30
40
50
RA
10
10,8
11,6
12,4
13,2
14
c)
RB
0
4
8
12
16
20
b) RA: y = 10+0,08x
RB: y = 0,4x
d) Bis 30 kWh ist Werk A teurer, ab 30 kWh ist A zunehmend günstiger. Beide Werke haben
bei ca. 30 kWh gleiche Gesamtkosten von ca. 12 € / kWh.
e) Beide Werke haben bei genau: 10+0,08x =0,4x  x= 31,25 kWh gleiche Gesamtkosten
f) 12,5€
Argumente: Grafisch ist anschaulich, aber ungenau…usw
11
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3 A,B,C,D Autovermietung
In der Graphik werden die Tarife von 2 Autovermietern A und B dargestellt.
a) Erklären Sie an Hand der Zeichnung welcher Autovermieter unter welchen
Bedingungen günstiger ist.
b) Bei wie viel km sind die Tarife gleich?
c) Ermitteln Sie die Gleichungen und überprüfen Sie Ihre Annahme durch eine
Rechnung.
d) Für ein dreitägiges Wochenende bieten A und B einen Sondertarif an,
20% Ermäßigung auf die Tagesgebühr.
Möglicher Lösungsweg:
a) ab 501 km Anbieter A günstiger. b)Gleicher Preis bei 500km,
c) A: y= 200, B: y = 150 in D = [100,300] und y = 75 + 0,25x für x>100
Überprüfung: 75 + 0,25x = 200 x=125/0,25 = 500
d) Für 3 Tage: A: 480.B: 3. 155. 0,8 + 108. 0,25 = 417.- B günstiger
12
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3-A, B Reisebudget
Der Leiter einer Kulturreise hat anfänglich ein Budget von € 1000,- für Trinkgelder,
Parkplatzgebühren und sonstigen kleineren Ausgaben zur Verfügung.
Er verbraucht im Schnitt pro Tag € 100,-.
a) Geben Sie eine Formel für den Restbetrag f(x) am Ende des x-ten Urlaubstages an!
b) Stellen Sie diese Funktion grafisch dar!
c) Am Anfang des 6. Tages erhält der Leiter noch weitere € 400,-, wie ändert sich dadurch
der Funktionsgraph? Wie lautet nun der Funktionsterm?
Möglicher Lösungsweg
a)
B C
C
2
rekusiv lin. Fkt.
3 x f(x)
f(x)
4 0 1000
1000
5 1 900
900
6 2 800
800
7 3 700
700
8 4 600
600
9 5 50
500
10 6 400
400
11 7 300
300
12 8 200
200
13 9 100
100
14 10 0
0
B
2
3
4
5
6
7
8
9
10
11
12
13
14
C
rekursiv
f(x)
1000
=$C$4-B5*100
=$C$4-B6*100
=$C$4-B7*100
=$C$4-B8*100
=$C$4-B9*100
=$C$4-B10*100
=$C$4-B11*100
=$C$4-B12*100
=$C$4-B13*100
=$C$4-B14*100
x
0
1
2
3
4
5
6
7
8
9
10
C
lin. Fkt.
f(x)
=1000-B4*100
=1000-B5*100
=1000-B6*100
=1000-B7*100
=1000-B8*100
=1000-B9*100
=1000-B10*100
=1000-B11*100
=1000-B12*100
=1000-B13*100
=1000-B14*100
b) f(x) = 1000 – 100.x
f(x)=1000-100x
1200
1000
800
600
400
200
0
0
2
4
6
8
10
12
c)
1000  100 x 0  x  5
f ( x)  
1400  100 x 6  x  14
f(x)
1200
1000
800
600
400
200
0
0
1
2
3
4
5
6
7
8
9
10
11
13
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV A,B,D Hell’s run – Skipiste
Im Schigebiet Silvretta Nova wurde eine neue Piste, der „Hell’s
Run“ eröffnet.
a) Was bedeutet 50% Gefälle? Dieser steile Teil der Piste ist
ca. 200 m lang.
b) Welcher Höhenunterschied wird in diesem Pistenabschnitt
überwunden?
c) Wie groß ist der entsprechende Steigungswinkel (ermitteln Sie
diesen aus einer maßstabsgetreuen Zeichnung)?
d) Ermitteln Sie die Steigung und die dazugehörige
Funktionsgleichung (der Endpunkt der Piste ist der
Koordinatenursprung)!
e) Ihr Freund behauptet, eine Skipiste kann unmöglich
100 % Steigung aufweisen. Hat er Recht? Dokumentieren und
argumentieren Sie Ihre Überlegungen!
Möglicher Lösungsweg:
a) Bei einer waagrechten Entfernung von 100 m beträgt der dazugehörige Höhenunterschied
50 m
b)PythagorasHöhenunterschied: 89,44m
c) Steigungswinkel: 26,57°
d) k = -0,5 Funktionsgleichung: y = -0,5 x
e) Bei einer waagrechten Entfernung von 100 m beträgt der dazugehörige Höhenunterschied
100 m (rechtwinkliges, gleichschenkliges Dreieck), Winkel 45 °, Steigung = 1 = 1. Mediane
IV 3-A Reinigungskosten
Eine Autobahnraststätte mietet zur Reinigung der Außenflächen (Parkplätze) eine
Kehrmaschine an, für welche Fixkosten von 400€ für je 10.000m² Reinigungsfläche
aufgewendet werden müssen. Die Reinigungskosten pro m² betragen 0,05€.
Ermitteln Sie die Gesamtkostenfunktion K(x) für die Reinigung einer Fläche von 0 bis
40.000m².
Möglicher Lösungsweg



K(x)  


0,05x  400 für 0  x  10000
0,05x  800 für 10000  x  20000
0,05x  1200 für 20000  x  30000
0,05x + 1600 für 30000  x  40000
14
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3A,B,D Bewegung
Die Formel v = a . t + v0 beschreibt die Geschwindigkeit nach einer bestimmten Zeit t,
wenn ein Fahrzeug beschleunigt bzw. bremst (a ist die Beschleunigung, t ist die Zeit und v 0
die Anfangsgeschwindigkeit).
a) Die allgemeine Funktionsgleichung einer Geraden lautet: f: y = kx+d
Welche Variablen der beiden Gleichungen entsprechen einander?
b) Ordnen Sie den Fahrten laut Grafik (siehe unten) die richtigen Gleichungen zu:
 v(t) = 10 – 4t
 v(t) = 2t + 10
 v(t) = 3t +10
 Eine Gleichung fehlt: Stellen Sie diese durch Ablesen aus der Graphik selbst auf!
c) Beschreiben Sie anhand des Verlaufs der einzelnen Graphen das Fahrverhalten der
Fahrer (1) bis (4).
d) Welcher Fahrer beschleunigt am stärksten? Begründen Sie Ihre Behauptung.
e) Welcher Fahrer kommt nach welcher Fahrzeit zum Stillstand?
f) Inwieweit stößt die Darstellung dieses Sachverhaltes (Zeit – Geschwindigkeit) durch eine
lineare Funktion eventuell an Grenzen?
Möglicher Lösungsweg:
a) d = vo, k = a, x = t, y = v
b) 10-4t …1 2t+10…2, 3t+10…3, 2t+15…4
c) 1. fährt mit 10 m/s und bremst ab mit 4m/s².
2. fährt mit 10 m/s und beschleunigt mit 2m/s².
3. fährt mit 10m/s und beschleunigt mit 3m/s².
4. fährt mit 15 m/s und beschleunigt mit 2m/s²
d) Am stärksten beschleunigt 1, er bremst mit 4m/s².
e) 1 kommt nach 2,5 s zum Stillstand: Nullstelle: 10 -4t = 0 --< t = 10/4 = 2,5s
f) Das Auto kann nur in kurzen Abschnitten gleichmäßig beschleunigen!
15
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3-A,B,C,D Kinoeintritt
In einem Salzburger Kino gelten folgende Eintrittspreise:
Einzeleintrittskarte € 6,00
Ermäßigte Eintrittskarte zu € 4,00 (Mitgliedsbeitrag € 10)
Wie oft muss man jährlich das Kino besuchen, damit sich die Mitgliedschaft gegenüber der
Einzeleintrittskarte rentiert?
a) Welche der Graphiken beschreibt den Sachverhalt? Begründen Sie Ihre Entscheidung!
b) Beschreiben Sie den Unterschied von homogener zu inhomogener linearer Funktion und
nehmen Sie auf das Beispiel Bezug.
c) Lesen Sie aus der Graphik das Ergebnis ab und erläutern Sie ob eine Mitgliedschaft Ihrer
Meinung nach sinnvoll ist!
Abb.1
Abb.2
Abb.3
16
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
Mögliche Lösung:
a) Abb.3
Die Funktion (Einzeleintritt € 6,00) geht durch den Ursprung, da man nur bezahlt, wenn man
das Kino besucht.
Die Funktion (Mitgliedsbeitrag) beginnt beim y-Wert 10 und steigt flacher als die andere
Funktion.
b) Homogene Funktion: y=kx; Die Funktion Einzeleintritt ist eine homogene lineare
Funktion, sie geht durch den Ursprung. y=6x
Inhomogene Funktion: y=kx+d; Die Funktion Mitgliedsbeitrag ist eine inhomogene lineare
Funktion und beginnt bei y=10. y=4x+10
c) Ab dem sechsten Kinobesuch zahlt sich eine Mitgliedschaft aus. Das ist sinnvoll, da
ich im Jahr ungefähr zehn Mal ins Kino gehe.
IV 3-C Eiskugeln
Interpretieren Sie den folgenden Graphen, der die Preisgestaltung von Eis in Stanitzeln in
zwei verschiedenen Eissalons darstellt.
Möglicher Lösungsweg
Grafik ist nicht korrekt, es handelt sich um eine diskrete Funktion!
1. Stanitzelpreis ist ablesbar: Die blaue Verkaufskurve ist eine homogene Gleichung, d.h. bei
diesem Eisverkäufer muss man nichts für das Stanitzel bezahlen, während die schwarze
Gerade eine inhomogene Gleichung ist, bei der der Stanitzelpreis 0,30€ beträgt.
2. Bei 3 Eiskugeln bezahlt man bei beiden gleich viel. Erst ab der 4. Eiskugel ist der
„schwarze“ Eisverkäufer günstiger.
Beide Verkaufskurven sind linear, das heißt sie haben die Gestalt: y = kx + d , x aus N
„blauer Eissalon“ g: y = 0,6 x , „schwarzer Eissalon“ f: y = 0,5.x + 0,3
17
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3-D Vinothek
Die Vinothek „St. Vinum” schaffte für einen neuen Verkostungsraum einen
Weinlagerschrank im Wert von € 5000,- an. Dieses Gerät hat nach 5 Jahren noch einen Wert
von € 400,-.
Beschreiben Sie an Hand der folgenden Darstellungen, welche die geeignetste Variante ist,
um den Restbuchwert der Maschine nach 3 Jahren zu ermitteln.
1) Tabellarisch
x
0
1
5
f(x)
5000
4080
400
2) Grafisch
3) Funktionsgleichung
Wert des Geräts nach x Jahren: f(x) = -920x + 5000 (xєN)
Möglicher Lösungsweg:
Wenn der Restbuchwert nach 3 Jahren ermittelt werden soll, so eignet sich die Tabelle nur
dann, wenn man weiß, dass die Abschreibung linear erfolgt, dann kann nämlich durch den
Unterschied der Werte zum Zeitpunkt 0 und zum Zeitpunkt 1 auf die weiteren Jahre
geschlossen werden. Die grafische Darstellung gibt einen guten Überblick aber durch die
Skalierung sind keine exakten Werte ablesbar. Die genaueste Darstellungsform ist die
Funktionsgleichung, hier muss nur für x der gesuchte Zeitpunkt (also hier 3) eingesetzt
werden und man kann den exakten Wert berechnen!
18
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3A,B,C Fledermaus
Fledermäuse „sehen“ schlecht. Zur Wahrnehmung benutzen sie das Ultraschallprinzip.
Das heißt: Sie stoßen Ultraschalltöne mit der Nase aus und fangen das Echo nach einer
bestimmten Zeiteinheit wieder mit den Ohren auf.
Auf diese Weise können sie sich auch bei Dunkelheit orientieren.
a) Für das Lufttier Fledermaus gilt: Die Ultraschalltöne der Fledermaus treffen nach
einer Sekunde auf einen 331 m entfernten Gegenstand.
Geben Sie eine Gleichung für die Zuordnung Zeit/Entfernung an
Zeichnen Sie einen „sinnvollen“ Graphen. Berücksichtigen Sie dabei die Größen Zeit und
Weg.
b) Bei einer sitzenden Fledermaus wurden die Zeitspannen zwischen Aussenden des
Ultraschalls und Auffangen des Echos, das von verschiedenen Insekten zurückprallte, mit:
1,7 s; 4 s; 1,4 s , 3 s gemessen.
Wie weit waren die Insekten jeweils von der Fledermaus entfernt?
Möglicher Lösungsweg:
a) Ohne Berücksichtigung der Eigengeschwindigkeit der Fledermaus gilt: s = 331 . t/2
s in m, t in s
b)
Messzeit
Entfernung
1,7
281,35
4
662
1,4
231,7
19
3 s
496,5 m
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3A,B, C, D Fahrrad
Julia fährt mit dem Fahrrad von ihrer Schule aus nach Hause. Dafür braucht sie
üblicherweise 18 Minuten. Auf ihrem Heimweg kommt sie an der Volksschule ihres kleinen
Bruders vorbei. Bis dorthin fährt sie 4 km und dann noch weitere 2 km bis sie zuhause
angekommen ist.
a) Berechnen Sie Julias Durchschnittsgeschwindigkeit.
b) Ihr Bruder legt seinen Heimweg zu Fuß zurück und ist dabei 4 km/h schnell. Wie lange
braucht er dafür?
c) Beschreiben Sie die Bewegung der beiden mit einer Weg-Zeit-Funktionen in der Form
s  v  t  s0 .
s...Weg (in km) v...Geschwindigkeit (km /h) t...Zeit (h)
s0...Anfangsentfernung zu Julias Schule
d) Berechnen Sie mit Julias Funktion wie lange sie bis zur Volksschule braucht. Das
rechnerische Ergebnis gilt natürlich nur unter gewissen Voraussetzungen. Welchen?
Nennen Sie Gründe warum diese eventuell nicht erfüllt sein könnten.
e) Zeichnen Sie die Graphen der beiden Funktionen in ein kartesisches
Koordinatensystem.
f) Berechnen Sie, wo und wann Julia ihren Bruder überholt. Kennzeichnen Sie diesen Punkt
im Koordinatensystem.
g) Wie viele Minuten ist Julia früher zu Hause? Kennzeichnen Sie diesen Zeitraum im
Graphen.
Möglicher Lösungsweg:
a) 20 km/h
b) 30 min
c)Julia: s  20  t ; Bruder: s  4  t  4
d) (12 Minuten): die Geschwindigkeit müsste konstant bleiben…
Zeitdifferenz
zwischen Julia und
Bruder
f) nach 5 km und 15 min
g) Julia ist 12 Minuten früher daheim.
20
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
Umkehrfunktionen
IV 3-AB Funktion oder nicht?
a) Handelt es sich bei der Zuordnung y = x² - 4 um eine Funktion?
b) Handelt es sich bei der Umkehrung, wenn man x und y vertauscht, um eine Funktion?
Möglicher Lösungsweg:
a) Mit EXCEL. Um die gestellte Frage beantworten zu können, erstellen wir eine
Wertetabelle.
Wir wählen beliebig für D = [ -3, 3]R , das heißt: Das Intervall zwischen - 3 und 3 in der
Menge der reellen Zahlen.
In der 2. Zeile schreiben wir in der 1. Zelle die Formel für den Funktionsterm
=A1^2-4. Wir ziehen unter der Definitionsmenge durch und erhalten:
-3
5
-2
0
-1
-3
0
-4
1
-3
2
0
3
5
6
Wir zeichnen den Graphen mit der
Diagrammoption von EXCEL:
5
4
3
2
1
y
0
-4
-3
-2
-1
-1
0
1
2
3
4
-2
-3
-4
Deutlich sehen wir in der Tabelle und auch in
der Grafik, dass es sich um eine Funktion
handelt, da es für jeden x-Wert nur genau
einen y-Wert gibt.
-5
x
b) Wir ändern in EXCEL nun ganz einfach die Reihenfolge der Reihen:
Graphik anklicken/ Datenquelle/ Reihe 1 und Reihe 2 vertauschen.
Wir erhalten das neue Bild:
4
3
2
1
y
0
-5
-4
-3
-2
-1
0
1
-1
-2
2
3
4
5
6
Und nun ist zu erkennen, dass es zu jedem xWert zwei y-Werte gibt, einen positiven und
einen negativen.
Die Umkehrung ergibt keine Funktion mehr.
Die Zuordnung ist nicht eindeutig. Man nennt
eine solche Zuordnung eine Relation.
-3
-4
x
21
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3-A,B,C Funktionen zeichnen und interpretieren
Zeichnen Sie mit einer vertrauten Technologie die folgenden Funktionen und übertragen Sie auch
die dazugehörende Wertetabelle. D = [-2,5 bis 2,5; Schrittweite 0,5]
f :xy
1
1
f2 : x  y  
f3 : x  y 
x4
3
1
1
x4
3
x²  4
3
f4 : x  y  
1
x²  4
3
a) Was fällt beim Vergleichen dieser vier Funktionen auf?
b) Welche Rolle spielen die Zahlen in den Gleichungen?
c) Für welche der vier Funktionen existiert eine Umkehrfunktion?
Geben Sie Ihren Funktionsterm an.
Möglicher Lösungsweg:
a, b) Die linearen
Funktionsgleichungen ergeben
Geraden.
Der Koeffizient vor x gibt den
Anstieg der Geraden: Die Gerade
steigt , wenn die Zahl positiv ist,
sie fällt , wenn die Zahl negativ ist,
jeweils mit k = 1/3, bzw k = -1/3
Die Zahlen +4 und -4 geben den
Durchgang der Funktionskurve
durch die y-Achse.
Die quadratischen Funktionen f3
und f4 ergeben Parabeln:
nach oben offen, wenn der
Koeffizient vor x² positiv ist, nach
unten offen, wenn er negativ ist.
Die Zahlen +4 und -4 geben den
Durchgang der Funktionskurve
durch die y-Achse.
c)
Die linearen Funktionen haben Umkehrfunktionen:
f1-1: y = 12 + 3x und f2-1 : y =12-3x
Die quadratischen Funktionen haben keine Umkehrfunktion, die Umkehrung ergibt die
Relationen :
R3: y   12  3x und R4: y   12  3x
22
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3-B,D Umkehrungen
Bestimmen Sie die Gleichung der Umkehrung von den gegebenen Funktionen und zeichnen
Sie die Graphen mit beiden Kurven.
Entscheiden Sie in jedem Falle, ob die Umkehrung zu einer Funktion oder zu einer Relation
führt.
a) y = 3x – 4
2
3
b) y  4  x
Möglicher Lösungsweg:
Beide angegebenen Funktionen
haben Umkehrfunktionen, sie sind
linear.
a) f-1 : y = (x+4)/3…rot
b) f-1 : y = (-x+4). 1,5…grün
23
Aufgabenpool für angewandte Mathematik / 1. Jahrgang
Bundes-ARGE
IV 3-A,B,C,D Echolot
Beim Echolot sendet man Schallwellen auf den Meeresgrund. Im Meereswasser beträgt die
Schallgeschwindigkeit 1452 m/s.
a) Nach welcher Funktionsgleichung berechnet man die Meerestiefe?
b) Ein Echolot hat bei fünf Messungen in einem Abstand von 50 m nach folgenden
Zeiteinheiten die vom Meeresboden zurückkehrenden
Schallwellen aufgezeichnet. Wie groß sind die
dazugehörigen Meerestiefen. Zeichnen Sie einen
möglichen Verlauf des Meeresbodens.
1,5s
1,2s
2s
1,1s
0,9s
c) Ein Echolot hat folgende Tiefen des
Meeresboden gemessen. 740 m; 1776 m; 1184 m;
2664 m. Geben Sie die dazugehörigen Zeiten an.
(Darstellung Wertetabelle)
d) Stellen Sie die Funktion Tiefe = f(Messzeit) dar.
Möglicher Lösungsweg:
a) y =1452. t / 2 y..Meerestiefe in m, t..Laufzeit des Signals in Sekunden (hin und retour)
b)
1,5
1,2
2
1,1
0,9 s
1089
871,2
1452
798,6
1089 m
c) Messzeiten:
740
1,0
1776
2,4
d)
24
1184
1,6
2664 m
3,7 s