Aufgaben - schule.at

Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
Quadratische Gleichungen und komplexe Zahlen
2 C Kleine Lösungsformel verstehen 1*)
Finden Sie für die quadratische Gleichung x2 -20x +q= 0 jeweils einen Wert für q,
sodass gilt:
Die Gleichung hat
a) 2 reelle Lösungen,
b) genau eine reelle Lösung
c) keine reelle Lösung?
Lösung:
Verwenden der kleinen Lösungsformel: x1,2 = +10± 100-q
Interpretieren: Dier Lösungsfälle hängen von der Diskriminante ab
a) 100 – q > 0  q < 100
b) 100 – q = 0  q = 100
c) 100 – q < 0  q > 100
2 B,C Kleine Lösungsformel verstehen 2
Finden Sie für die quadratische Gleichung x2 +px+36 = 0 jeweils einen Wert für p,
sodass gilt:
Die Gleichung hat
a) 2 reelle Lösungen,
b) genau eine reelle Lösung
c) keine reelle Lösung?
Lösung:
p æp ö
Kleine Lösungsformel verwenden: x1,2 = - ± ç ÷ -36
2 è2ø
2
p2
-36 = 0  p2 = 144  p = ±12
4
a) p > 12
oder
p < -12 …jeweils 2 reelle Lösungen
……x² + 14x + 36 = 0 ---L={-3.39,-10,6}, x² -14x + 36 = 0---L = {3.39,10,6}
b) p = 12
oder
p = -12… jeweils 1 reelle Lösung
x² + 12 x + 36 = 0 L = {-6} und x² -12x + 36 = 0 …L ={6}
c) p < 12
oder
p > -12 … keine reelle Lösung, jeweils 2 komplexe Lösungen
x² + 10 x + 36 = 0 … L = {-5 ±3,32i }
x² - 10 x + 36 = 0 … L = {5 ±3,32i }
*..Natürlich können diese Aufgaben auch mit der großen Lösungsformel gemacht werden!
1
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
2 B,C,D Quadratische Gleichung
a) Erklären Sie die Definition der Zahl i und den Begriff „komplexe Zahl“ . Erläutern Sie, wie man diese
Zahlen grafisch darstellen kann.
b) Die Multiplikation der beiden folgenden Terme (Linearfaktoren) ergibt einen gemischt
quadratischen Term.
1. Term: x - 2 - 3i
2. Term: x - 2 + 3i
Stellen Sie eine quadratische Gleichung auf, indem Sie das Produkt der beiden angegeben Terme
gleich Null setzen.
c) Lösen Sie die in b) erhaltene Gleichung und stellen Sie die Lösungen grafisch dar.
d) Diskutieren Sie, wie die erhaltenen Lösungen in c) mit den Termen in der Angabe
zusammenhängen.
Lösung
a) Argumentieren
Die Zahl i wird über die Gleichung i² = -1 definiert.
-1 = i nennt man die imaginäre Einheit. In der sogenannten Gauß’schen Ebene wird diese Einheit in
der y- Richtung des Koordinatensystems verwendet, um die imaginären Zahlen darzustellen.
Komplexe Zahlen sind die Summe oder Differenz einer reellen Zahl = Realteil und einer imaginären
Zahl = Imaginärteil. In der Gauß’schen Ebene werden sie durch einen Punkt (oder Pfeil vom Ursprung
zu diesem Punkt) dargestellt. Die x-Koordinate bezeichnet den Realteil, die y-Koordinate den
Imaginärteil.
b) Operieren
Die Terme werden multipliziert:
(x - 2 - 3i) (x - 2 + 3i) = x² - 2x - 3xi - 2x + 4 + 6i +3ix - 6i - 9 i² = x² - 4x + 13 (dabei wurde
berücksichtigt, dass -9i² = +9 ist!)
Das Produkt wird gleich 0 gesetzt
x² - 4x + 13 = 0 Als Lösung erhält man: x1 = 2 + 3i und x2 = 2 - 3i
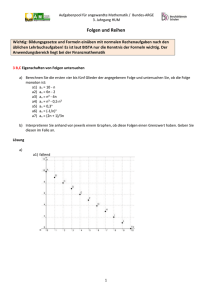
c) Grafisch interpretieren
d) Term 1 ist x – x1
Term 2 ist x – x2
Die quadratische Geleichung besteht aus dem Produkt der
Linearfaktoren (x – x1 )(x – x2 ) = 0
Wenn der Vieta’sche Satz bekannt ist, dann könnte man diesen
anwenden: p = - (x1+x2), q = x1 . x2 ….
2
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
2A,B,C Straßenverbreiterung
Ein Grundstück liegt an einer Straßenkreuzung. Die Straße soll verbreitert werden, daher kommen
ein Streifen von 1,5 m Breite von der Grundstücklänge und ein Streifen von 2,5 m von der
Grundstückbreite weg.
Die Länge des ursprünglichen Grundstücks war 20-mal länger als seine Breite und seine Fläche
beträgt nach der Abgabe 2 400 m².
a) Zeichnen Sie eine Skizze, die diese Situation veranschaulicht.
b) Stellen Sie die quadratische Gleichung in der Form ax² + bx + c = 0 auf, mit der man eine Seite des
ursprünglichen Grundstücks berechnen kann.
c) Berechnen Sie, wie viel Prozent des ursprünglichen Grundstücks die Straßenerweiterung gefordert
hat.
d) Ein Kollege von Ihnen kam in seiner Berechnung auf die folgende Gleichung für die Seite a des
Grundstücks: a² - 51,5a + 47 925 = 0. Er fragt Sie, wie er die Lösung dieser Gleichung interpretieren
solle, wo auf dem Zahlenstrahl diese Lösungen liegen und möchte wissen, welchen Fehler er
gemacht hat.
Lösung:
a) Transferieren und Interpretieren
b) Modellieren
a = 20 b
(a - 1,5) (b - 2,5) = 2 400  (20b -1,5)  (b -2,5) = 2400  20 b² - 51,5 b -2396,25 = 0
c) Operieren, Technologieeinsatz und Interpretieren
Ursprüngliches Grundstück aus b) mit Technologie  b = 12,31m a = 246,17 m
A = 3 030,72 m²
Abgetretenes Grundstück: 615,425 + 14,715 = 630,14 m², das sind ca. 20,8% des ursprünglichen
Grundstücks.
d) Operieren, Interpretieren, (evt. modellieren) und argumentieren
Die Lösung der Gleichung: 25,75 ± 217,4 i
Es sind komplexe Zahlen, die nicht auf dem Zahlenstrahl liegen, sondern als Punkte in der
Gauß’schen Ebene dargestellt werden. Die Koordinaten: x-Richtung 25,75 der Realteil und y-Richtung
217,4 – der Imaginärteil.
Die Gleichung des Kollegen hat daher keine Lösung für das Grundstück..
Sie machen vielleicht folgende Überlegung: Die Gleichung hätte nur dann reelle Lösungen, wenn das
Vorzeichen bei 47 925 negativ wäre. Dann ergäbe sich die Lösung: 246,17 und -194,68. Die positive
Lösung kommt in Frage und sie stimmt mit Ihrer Berechnung überein.
Sie können den Fehler aber auch finden, wenn Sie die Modellierung der Gleichung neu beginnen. Sie
kommen dann zur Gleichung a² - 51,5a - 47 925 = 0
3
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
2A,B,D Liegewiese
In einer öffentlichen Badeanlage ist das Kinderbecken kreisförmig und hat 10 m im Durchmesser. Das
Becken liegt im Zentrum einer quadratischen Liegewiese. Die Liegefläche ist vierfach so groß wie die
Fläche des Beckens.
a) Erstellen Sie eine Skizze, die die Situation beschreibt.
b) Berechnen Sie di e Fläche der Liegewiese.
c) Modellieren Sie die quadratische Gleichung in der Form: ax²+ bx + c = 0, sodass es möglich ist, die
Seite x der Liegewiese zu berechnen.
d) Lösen Sie die von Ihnen erstellte Gleichung und überprüfen Sie die Lösung auf ihre Brauchbarkeit.
e) Nehmen Sie an, die Liegewiese würde in Form eines Kreisrings um das Becken liegen und auch
vierfach so groß wie die Fläche des Beckens sein. Stellen Sie die entsprechende Gleichung der
Form: ax²+ bx + c = 0 auf, mit der man die Breite x der Liegewiese berechnen könnte.
Lösung
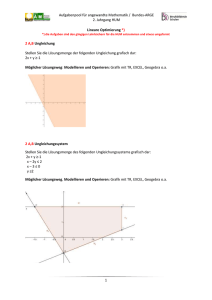
a) Transferieren
b) Operieren
Beckenfläche r² π = 25 π = 78,54 m²
Die Liegewiese hat eine Fläche von 314,16m²
c) Modellieren
x² = 5  78,54. Es ist eine rein quadratische Gleichung.
d) Operieren und kommentieren
Lösung: ± 19,82 m.
Brauchbar ist nur die positive Lösung
e) Modellieren
Die Gesamtfläche wäre: R²π = 5  25 π , R = 5 + x
(5 + x)² = 125
x² + 10x -100 = 0
(Lösung wäre 6,18 m, nicht gefordert)
4
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
2 A,B Fahrzeit
Ein Abschnitt von 10 km einer Autobahn sind von Baustellen befreit worden, so dass sich dort die
mittlere Geschwindigkeit um 40 km/h gegenüber der auf dieser Strecke vorgeschriebenen
Geschwindigkeit erhöhte. Die Fahrzeit verringert sich dadurch auf dieser Strecke um 2,5 Minuten (=
1/24 Stunden).
a) Stellen Sie die quadratische Gleichung in allgemeiner Form at² + bt + c = 0 auf, mit der man die
gesamte neue Fahrzeit t (in Stunden) berechnen kann.
b) Berechnen Sie die Geschwindigkeit, mit der das neu freigegebene Straßenstück im Mittel befahren
wird!
Lösung
a) Modellieren
Tabellarisches Ordnen
Weg in km
Geschwindigkeit in km/h
jetzt: 10
v = 10 /t
vorher: 10
v – 40 = 10/t - 40
Weg = Geschwindigkeit mal Zeit
Zeit in h
t
t + 1/24
1 
 10
 
10 = 
- 40    t +
 .....mal 24 und mal t
 t
  24 
240t = (10 - 40t)  (24t + 1)
0 = - 960 t² - 40t + 10
96 t² + 4t - 1 = 0
b) Operieren
Neue Zeit: aus a) berechnen: t =0,0833 h Geschwindigkeit: 10 / t = 120 km/h
Man fährt ohne Baustelle auf dieser Strecke mit ca. 120 km/h.
5
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
2 A,B,C Laufen und Radfahren
Eine Sportlerin läuft oder fährt mit dem Rad regelmäßig die Strecke von 12 km.
Mit dem Fahrrad gewinnt sie ca. eine halbe Stunde und ist etwa 6 km/h schneller unterwegs.
a) Stellen Sie die quadratische Geleichung auf, mit der man die Laufgeschwindigkeit berechnen kann.
b) Berechnen Sie, wie schnell die Sportlerin durchschnittlich mit dem Rad unterwegs ist und wie
lange sie für diese Strecke in beiden Fällen braucht.
Lösung:
a) Modellieren
Tabellarisches Ordnen
Weg in km
Geschwindigkeit in km/h
Laufen: 12
v
Rad : 12
v +6
Weg = Geschwindigkeit mal Zeit
12 = (v+6)  (12/v – 0,5)
12v = (v+6)  (12 – 0,5 v)
0,5 v² + 3v – 72 = 0
b) Operieren und interpretieren
v = ca. 9,37 km/h Laufgeschwindigkeit
15, 37 km/h ist die Radgeschwindigkeit
Dauer für Laufen: 1,28 h = ca. 1 h und 17 Minuten
Dauer mit Rad: 0,78h = ca 47 Minuten
6
Zeit in h
t = 12 /v
t – 0,5 = 12 / v - 0,5
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
2 A,B Theaterkarten
Für die Belegschaft einer Firma werden Extravorstellungen im Theater gebucht. Der Preis für die
Vorstellung insgesamt beträgt € 1.200,-.
Nun kommen 10 Angestellte mehr als vorgesehen waren, dadurch wird die Karte pro Person um 50
Cent billiger.
a) Fassen Sie den Text tabellarisch geordnet in mathematischer Schreibweise zusammen
b) Stellen Sie die quadratische Gleichung in der allgemeinen Form ax² + bx+ c = 0 auf, mit deren Hilfe
man die Anzahl x der Personen berechnen kann, die ursprünglich für die Vorstellung vorgesehen
waren.
c) Berechnen Sie die Anzahl der Personen , die in der Theatervorstellung waren und den Preis , den
sie jeweils pro Person bezahlen mussten.
Lösung
a) Transferieren
vorgebucht
tatsächlich
Preis pro Person
1200 / x
1200 / (x+10)
Anzahl der Personen
x
x+10
b) Modellieren
1200
1200
- 0,5 =
x
x +10
1200x  12000  0,5x²  5x 1200x
0,5x²  5x  12000  0
b) Operieren / Technologieeinsatz
vorgebuchte Plätze: x = 150
tatsächlich benötigte Plätze: 160
Preis pro Person 1200 / 160 = € 75,-
7
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
Anhang:
Umwandlung von Formeln mit quadratischen Größen samt Interpretationen und Argumentationen
Sie sind hier besonders erwähnt, weil solche Aufgaben für alle Arten von Aufnahmeprüfungen in
den tertiären Bereich wichtig sind. Die Aufgaben sind nicht schwierig, werden aber meist von den
Schülerinnen und Schülern wegen des kompliziert aussehenden Kontexts nicht gekonnt. Daher ist
eine diesbezügliche Abklärung sehr günstig.
Bei der sRDP geht man davon aus, dass solche Formelumwandlungen – egal in welchem Kontext –
niemals ein Problem sein sollten.
B,D Schwerkraft
Ein Körper mit der Masse m wird im Schwerefeld der Erde (Masse M) angezogen. Die Kraft F ist
durch die folgende Formel beschreibbar:
F  G
mM
r²
F Kraft in Newton N, m und M beide beteiligten Massen in kg, r… Abstand der beiden
Massen(mittelpunkte) in Meter. G = eine konstante Zahl, (Gravitationskonstante = 910-9 Nm²/kg²)
a) Argumentieren Sie anhand der gegebenen Formel, wie die Entfernung r die Schwerkraft F
zwischen 2 Körpern mit den Massen m und M beeinflusst.
b) Formen Sie die Formel nach der Größe r um.
Lösung
a) Argumentieren:
Wenn die Entfernung r zwischen den Massen wächst, dann wird die Schwerkraft kleiner. die
Abnahme der Schwerkraft ist nicht indirekt proportional zu r sondern zu r².
Wenn r doppelt so groß wird, dann nimmt die Schwerkraft auf ¼ ab.
Wird r halbiert, dann wächst die Schwerkraft auf das Vierfache.
b) Operieren
GmM
r
F
8
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
2 B,C,D Energie
Die Energie E eines Körpers mit der Masse m, der im Schwerefeld der Erde mit der Geschwindigkeit v
frei herunter fällt, lässt sich in jedem Moment durch die folgende Formel beschreiben:
mv²
2
E = Energie in Joule (J) , Fg ..Schwerkraft in Newton (N), h in Meter (m),
m= Masse in Kilogramm (kg), v = momentane Geschwindigkeit in Meter pro Sekunde (m/s)
E = Fg  h +
a) Formen Sie die Formel nach der Größe v um.
b) Interpretieren Sie die beiden Lösungen und entscheiden sie, welche die Situation des freien Falls
beschreibt.
c) Argumentieren Sie, wie sich die Geschwindigkeit durch die Höhe verändert, in der sich der Körper
mit der Energie E gerade befindet. Berechnen Sie dazu einige Werte zur Demonstration Ihrer
Überlegungen für eine Energie E = 100 J und einer Schwerkraft Fg = 10 N.
Lösung:
a) Operieren:
mv²
 E  Fg  h
2
2(E  Fg  h)
v
m
b) Interpretieren, Argumentieren: Die beiden Lösungen unterscheiden sich nur durch das
Vorzeichen, welches die Richtung der Geschwindigkeit angibt. Man muss daher festlegen, wie man
das in der Diskussion halten will. z.B. die Richtung zum Erdmittelpunkt wird negativ definiert und
eine Aufwärtsbewegung = Gegenrichtung positiv
Dann gilt die Lösung:
2(E  Fg  h)
v
für den freien Fall.
m
c) Argumentieren: Bei großer Höhe wird die Größe E  Fg  h kleiner, daher ist dort auch die
Geschwindigkeit v betragsmäßig kleiner, bei kleinem h wird die Geschwindigkeit größer, die Zunahme
ist nicht proportional zu h.
h =E/Fg = 10m  Wurzel ist = 0 und v = 0 die Starthöhe h kann nicht größer als 10 sein!
h = 9  v= ca. 4,5m/s; h = 8 m  v = ca. 6,3; h = 7  v =ca. 7,5m/s
Am höchsten Punkt ist die Geschwindigkeit = 0, die Geschwindigkeit nimmt betragsmäßig zu, wenn
h kleiner wird, aber nicht im gleichen Maße wie h abnimmt.
9
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
2A,B,C,D Tennisball
Ein Tennisball wird von einem Balkon aus mit der Geschwindigkeit v0 = 13,89 m/s lotrecht nach oben
geschossen. Der Abschusspunkt auf dem Balkon ist s0 = 3 m über dem Boden vor dem Haus. Der Ball
steigt senkrecht auf, erreicht den höchsten Punkt und fällt wieder hinunter. Die Erdbeschleunigung
beträgt g = 9,81 m/s².
Bezeichnungen: Weg s in Meter (m), Geschwindigkeit v im Meter pro Sekunde (m/s),
Zeit t in Sekunden (s).
g
Zusammenhänge: Lotrechter Wurf nach oben: v = v0 – g∙t
s = s0 + v0∙t –  t²
2
a) Zeichnen Sie eine Skizze zu dieser Situation
b) Berechnen Sie die Steigzeit und Steighöhe des Balls (Höhe in Bezug auf den Boden).
c) Erklären Sie anhand einer Skizze, wie man die Geschwindigkeit berechnen kann, mit
der der Ball die Horizontalebene 5 m über dem Abschusspunkt durchschneidet.
d) Berechnen Sie die Geschwindigkeit, mit der der Ball am Boden vor dem Haus auftrifft
und die gesamte Zeitdauer, wie lange der Ball unterwegs ist.
e) Der Ball springt nach Auftreffen auf dem Boden wieder hoch. Berechnen Sie die
nächsten 2 Höhen, die er in weiterer Folge noch erreichen würde, wenn man die
Höhenverluste mit 25% je Aufschlag annimmt.
f) Erklären Sie, wie man die Rechnung ansetzen müsste, wenn man herausfinden will,
wie oft der Ball am Boden auftrifft, bis seine Steighöhe weniger als 1 m beträgt.
Lösung:
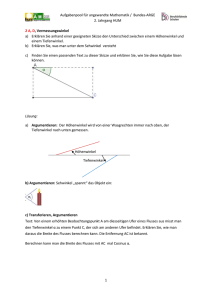
a) Transferieren und Interpretieren:
b) Operieren Steigzeit: v =
=0
(Geschwindigkeit im Umkehrpunkt v = 0 km/h)
t = 1,4159 s
Steighöhe: s =
= 12,83 m über
dem Boden bzw 9,83 m über dem Abschusspunkt.
c) Argumentieren: Geschw. in 5m über dem
Abschusspunkt = 8 m über Boden, kann man
berechnen, indem man die Gleichung:
8=
löst. Man erhält 2
Lösungen für t, denn die Horizontalebene wird
zweimal durchstoßen, bei der Aufwärtsbewegung
und nach der Umkehr nochmals beim Fall nach
unten.
Die Lösungen von t sind in die Formel für v
einzusetzen. Man erhält für v einen positiven Wert
für das Aufsteigen zu 5m Höhe über dem Balkon und die gleich große Zahl negativ für das
Herabfallen auf die Höhe von 8m über dem Boden.
10
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
d) Modellieren, Operieren und Interpretieren:
s = 0  3 + 13,89t – 4,905 t² = 0
Lösungen: t1 =-0,201 (negative Zeit  keine Lösung) t2 = 3,033 s
Die gesamte Bewegung dauert 3,033 Sekunden.
v = 13,89 – 9,81 3,033 = -15,87 m/ s ( negatives Vorzeichen bedeutet, dass die Richtung
nach unten geht)
e) Operieren
h0 = 9,83 + 3 = 12,83
nach dem 1. Aufprall : 12,83 0,75 = 9,6225 m = h1
nach dem 2. Aufprall : 9,6225 0,75 = 7,216875 m = h2
f)
Modellieren, argumentieren:
Man könnte zum Beispiel mit Excel die Liste aus Aufgabe e) fortführen
nach dem 3. Aufprall: 7,216875 0,75 = 5,412656 m = h3
nach dem 4. Aufprall: 5,412656
= 4,05949 m = h4
nach dem 5. Aufprall: 4,05949 0,75 = 3,044619 m = h5
nach dem 6. Aufprall: 3,044619
= 2,28346 m = h6
nach dem 7. Aufprall: 2,28346 0,75 = 1,712598 m = h7
nach dem 8. Aufprall: 1,712598 0,75 = 1,28445 m = h8
nach dem 9. Aufprall: 1,28445 0,75 = 0,96334 m = h9
Oder man überlegt sich, dass immer mit 0,75 multipliziert wird und löst die Gleichung
12,83  0,75n = 1 mit Technologieeinsatz
n = 8,87  nach dem 9. Aufprall ist es unter 1m
11