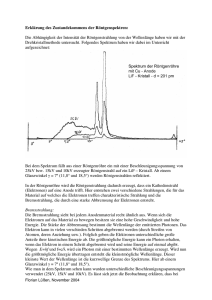
Fotoeffekt-Potenzialtopf

Von Fynn, Patrick und Malte
Abituraufgaben
1 Äußerer Photoelektrischer Effekt
Das Licht einer Quecksilberdampflampe (Hg-Lampe) beleuchtet nach der in Abbildung 1
dargestellten Anordnung eine Vakuumfotozelle. Durch unterschiedliche Filter fällt nur Licht
mit den in Tabelle 1 aufgeführten Wellenlängen auf die Fotokathode.
1.1
Erläutern Sie die Vorgänge in der Fotozelle unter Berücksichtigung der Messwerte aus der
Tabelle 1 und gehen Sie dabei auf die Funktion der einzelnen Komponenten im
Versuchsaufbau (siehe Abbildung 1) ein. Stellen die Energiebilanz für die Vorgänge in der
Fotozelle auf.
Das Licht der Hg-Dampflampe trifft auf einen Filter. Dieser filtert die gewünschte Wellenlänge λ
aus dem Gesamtspektrum der Dampflampe heraus. Das gefilterte Licht wird anschließend durch
eine Blende fokussiert und trifft am hinteren Ende der Fotozelle auf die Fotokathode, ohne mit der
Ringanode zu wechselwirken. Zwischen Ringanode und Fotokathode wird die Spannung U
gemessen.
Abhängig von der Energie des Lichts gemäß
werden Elektronen mit der
Kinetischen Energie
emittiert. Diese emittierten Elektronen
durchqueren den Raum, treffen (teilweise) auf der Ringanode ein und laden diese negativ auf.
Zwischen positiver Fotokathode und negativer Ringanode entsteht eine Spannung. Darauf folgende
Elektronen müssen gegen das durch die schon vorhandenen Elektronen erzeugte elektrische Feld
arbeiten. So pendelt sich die Spannung auf einen fixen Wert ein. In der Tabelle sind die gemessenen
Spannungen in Abhängigkeit der Wellenlänge aufgelistet.
Es fällt auf, dass mit steigender Frequenz (also sinkender Wellenlänge) die Spannung U steigt. Da
für die Energie der Zusammenhang
(q ist in diesem Fall die Elementarladung des
-19
Elektrons ≈ 1,6*10 C) gilt, steigt mit steigender Energie der Elektronen auch die Spannung.
Erklären lasst sich dieses Phänomen durch den eben beschrieben fixen Spannungswert.
Die Energie des Photons
wird abgegeben an das Elektron.
Von Fynn, Patrick und Malte
1.2
Berechnen Sie zu den angegebenen Wellenlängen die zugehörigen Frequenzen. Zeichnen Sie
das f - Ekin- Diagramm (Rechtsachse ist f, Hochachse ist Ekin) für die benutzte Kathode.
Wellenlänge λ in nm
405
436
546
579
Frequenz f in 1014 Hz Umax in V
7,4
0,81
6,88
0,59
5,49
0,02
5,18
0
Ekinetisch in eV
0,81
0,59
0,02
0
0,9
y = 0,379x - 2,011
0,8
0,7
0,6
7,4
0,5
6,88
0,4
5,49
0,3
5,18
0,2
0,1
0
-0,1 0
1
2
3
4
5
6
7
8
1.3
Deuten Sie die Steigung und die Achsenabschnitte des Diagramms als physikalische Größen.
Zeigen Sie, dass das verwendete Kathodenmaterial Kalium eine Austrittsarbeit E Austritt ≈ 2,25
eV besitzt. Ermitteln Sie die Grenzfrequenz sowie das Planksche Wirkungsquantum h.
Zeichnen sie in das f - Ekin- Diagramm zusätzlich den zu erwartenden Graphen für den Fall,
dass als Kathodenmaterial Cäsium (EAustritt ≈ 1,94 eV) verwendet wird.
Die Steigung der im Diagramm eingezeichneten Ausgleichsgerade entspricht dem Plankschen
Wirkungsquantum, da
gilt. Den Schnittpunkt der Kurve mit der X-Achse nennt man
Grenzfrequenz, also die Frequenz, bei der sich die Elektronen aus dem Metall lösen. Es gilt hier
also
.
Berechnung des Plankschen Wirkungsquantums
Aus dem Diagramm geht die Nullstelle der Kurve, also die Grenzfrequenz bei x = 5,31 hervor. Als
zweiten Wert für die Berechnung der Steigung eignet sich der Punkt (7,4|0,81). Vorerst muss jedoch
die Energie in Joule umgerechnet werden.
Steigung
ist dem tatsächlichen Wert des Plankschen Wirkungsquatums von
sehr nahe.
Von Fynn, Patrick und Malte
Grenzfrequenz
Um die Austrittsarbeit des verwendeten Metalls zu bestimmen, setzen wir in die Gleichung
die Grenzfrequenz ein.
Die Austrittsarbeit für Kalium beträgt somit ungefähr 2,25eV.
Cäsium-Graph
0,9
0,8
Kalium
(Messwerte)
0,7
0,6
0,5
Cäsium
0,4
0,3
0,2
0,1
Linear (Kalium
(Messwerte))
0
-0,1 0
2
4
6
8
Um den Graphen für die Cäsium Kathode zeichnen zu können ist es lediglich von Nöten, die
spezifische Grenzfrequenz zu bestimmen, da die Steigung des Graphen immer die Naturkonstante h
ist.
1.4
In einem weiteren Experiment wird der Durchmesser der Blende vor der Fotozelle (siehe
Abbildung 1) verkleinert. Geben sie die zu erwartenden Beobachtungen begründet an.
Es ist zu erwarten, dass die gemessene Spannung gleich bleibt, jedoch die Stromstärke im Leiter
abnimmt. Erklärung im 2. Teil.
Die Deutung des Fotoeffektes ist mit dem klassischen Wellenmodell nicht zu vereinbaren.
Stellen sie die Widersprüche zum Wellenmodell dar und deuten sie den Effekt im
Quantenmodell.
Da durch die verkleinerte Blende nun weniger Licht auf die Fotozellen fällt, die Intensität des
Lichtes also abnimmt, ist damit zu rechnen, dass die Anzahl der Elektronen, welche von der
Fotokathode zur Anode wandern zurückgeht, da im Quantenmodell eine niedrigere Intensität eine
geringere Photonendichte bedeutet.
Die einzelnen Lichtquanten besitzen allerdingst noch immer die selbe Energie und somit sind die
Von Fynn, Patrick und Malte
herausgelösten Elektronen keiner qualitativen Beeinträchtigung unterworfen, an der Spannung
ändert sich also nichts.
Dem klassichen Wellenmodell nach würde eine abnehmende Lichtintensität auch eine Abnahme des
Energiegehaltes des Lichtes bedeuten und somit wären die herausgeschlagenden Elektronen
langsamer. Die energieärmeren Elektronen führten nun zu einem Spannungsabfall, da
gilt.
1.5
Ohne Filter zwischen Hg-Lampe und Fotozelle ergibt sich (mit einer Kalium Fotokathode)
der Messwert
erklären sie diesen Sachverhalt.
Da Quecksilberdampflampen auch ultraviolettes Licht erzeugen, welches vorher herausgefiltert
wurde, und dieses eine besonders hohe Frequenz besitzt (geringe Wellenlänge), also besonders
energiereich ist, sind auch die aus dem Metall emittierten Elektronen energiereicher. Das führt zu
einer höheren fixen Spannung.
Von Fynn, Patrick und Malte