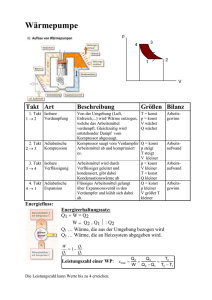
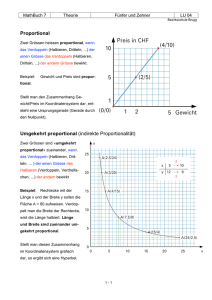
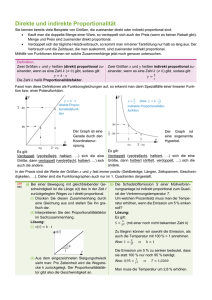
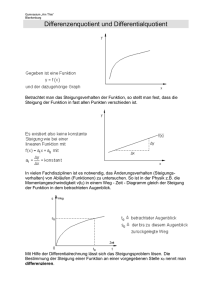
DiffGl

Differentialgleichungen
1.
Einführung
In vielen Gebieten der Wissenschaft beschäftigt man sich mit dynamischen Modellen, d.h. mit
Modellen, in denen sich bestimmte Grössen in Abhängigkeit von der Zeit ändern.
Physik:
Chemie:
Ökonomie:
Radioaktiver Zerfall, Ausbreitung von Wellen
Konzentration von Reagenzien bei verschiedenen Reaktionen
Volkseinkommen, Investitionen oder Konsum
Als Instrument zur Analyse von dynamischen Systemen dienen Differentialgleichungen.
Ziele einer dynamischen Analyse sind:
Steuerung, um einen Gleichgewichtszustand zu erhalten
Prognosen von bestimmten Werten in der Zukunft
Stabilitätsbetrachtungen
2.
Was ist eine Differentialgleichung?
Eine gewöhnliche Differentialgleichung beschreibt, wie eine unbekannte Funktion y(x) oder y(t)
und ihre Änderung y'(x) (eventuell auch höhere Ableitungen) zusammenhängt. Kommen
mehrere unabhängige Variablen vor, so heisst die Differentialgleichung partiell. Die folgenden
Ausführungen beziehen sich ausnahmslos auf gewöhnliche Differentialgleichungen.
Bezeichnung:
dy
y  
dx
Beispiel:
Def:
y'(t) = a y(t)
(Der Funktionswert ändert sich proportional zum jeweiligen Wert)
Eine Gleichung der Form
F(x, y, y', y'', ..., y(n)) = 0
bzw.
y(n) = F(x, y, y', y'', ..., y(n- 1))
heisst Differentialgleichung n-ter Ordnung.
Treten y, y', y'', ..., y(n- 1) nur linear auf, d.h. Vielfache der Funktion und ihrer
Ableitungen werden addiert oder subtrahiert, aber nicht multipliziert miteinander, so
heisst die Differentialgleichung linear. Die Koeffizienten können dabei konstant oder
Funktionen der unabhängigen Variablen x oder t sein.
Beispiele:
1)
2)
3)
4)
5)
y' = y
y'' = 1
y'' + 3y' - 10y = ex
y' + x2y = a + bx3
y'' + y'y = c
Lin. DG 1. Ordnung mit konst. Koeffizienten
Lin. DG 2. Ordnung mit konst. Koeffizienten
Lin. DG 2. Ordnung mit konst. Koeffizienten
Lin. DG 1. Ordnung mit nicht konst. Koeffizienten
Nicht lineare DG 2. Ordnung
3.
Was ist die Lösung einer Differentialgleichung?
Sucht man die Lösung einer Differentialgleichung, so sucht man Funktionen y(x) oder y(t), die
diese Differentialgleichung erfüllen.
Beispiel:
y'(x) = y(x)
Lösungen:
y(x) = 0
y(x) = ex
y(x) = kex
Def: Die allgemeine Lösung einer Differentialgleichung ist die Gesamtheit aller Funktionen,
welche die vorgeschriebene Gesetzmässigkeit aufweisen.
Anfangsbedingungen lassen die Bestimmung einer einzigen Lösung aus der Lösungsgesamtheit
zu.
Beispiele:
4.
1)
2)
3)
4)
5)
y' = x
Lösung:
y'' = 1
Lösung:
R'(t) = -kR(t) (Radioaktiver Zerfall)
Lösung:
Beweise: y'' + y = 0 hat die Lösungen y = cos x und y = sin x
Beweise: x2y'' - 3xy' + 4y = 0 hat die Lösung y = x2 ln x
Wie entstehen Differentialgleichungen?
Beispiel 1:
Radioaktiver Zerfall
Das radioaktive Isotop Thorium-234 zerfällt mit einer Rate, die proportional zum aktuellen
Bestand ist, d.h. je kleiner der Bestand an Thorium-234 ist, desto kleiner wird die Abnahme des
Bestandes.
Um einen solchen Zerfallsprozess mathematisch zu erfassen, nehmen wir an, der Bestand an
Thorium-234 zum Zeitpunkt t sei R(t)>0, wobei R in Milligramm und t in Tagen gemessen wird.
Dieser Bestand ändert sich im Laufe der Zeit. Die Abnahme des Bestandes R(t) in einem
bestimmten Zeitraum [t, t+h] ist abhängig von der Länge des Zeitintervalls h und vom jeweiligen
R(t).
dR
Lassen wir h gegen 0 gehen, so erhalten wir die momentane Änderung des Funktionswertes
.
dt
Die phylikalische Beobachtung, dass Thorium-234 mit einer Rate abnimmt, die proportional
dR
zum aktuellen Bestand ist, bedeutet, dass die momentane Veränderung
proportional zu R ist.
dt
Also erfüllt R die Differentialgleichung
dR
 kR .
dt
Beispiel 2:
Harmonische Schwingungen
Einige der bedeutendsten Anwendungen von Differentialgleichungen erster Ordnung findet man
in der Mechanik, z. B. bei der Bewegung eines Körpers entlang einer geraden Linie. Wir gehen
davon aus, dass sich die Körper gemäss dem Newtonschen Grundgesetz der Mechanik verhalten:
Das Produkt aus Masse m und Beschleunigung a ist gleich der resultierenden Kraft F
F ma
Ein Gegenstand wird aus der Ruhelage fallengelassen.
Wir gehen davon aus, dass der Versuch nicht im
Vakuum ausgeführt wird, d. h. es gibt einen Widerstand
der proportional zum Absolutbetrag der momentanen
Geschwindigkeit v des Gegenstandes ist.
Unter der Annahme, die Gravitationskraft sei konstant,
wollen wir die Position und die Geschwindigkeit des
Gegenstandes zu einem bestimmten Zeitpunkt t bestimmen.
kv
mg
In diesem Beispiel ist es geschickt, die x-Achse nach unten
x
zu richten. Der Ursprung liegt im Ausgangspunkt des
Gegenstandes, wie die nebenstehende Skizze zeigt.
Die Gewichtskraft mg, die auf den Gegenstand wirkt, wirkt so nach unten, in positiver xRichtung. Der Widerstand k v , wobei k eine positive Konstante ist, wirkt der Gewichtskraft
entgegen (in negativer x-Richtung) und bremst die Bewegung. Deshalb kann das Newtonsche
Grundgesetz der Mechanik folgendermassen geschrieben werden:
m
5.
dv
 mg  kv
dt
oder
dv k
 vg
dt m
Qualitative Analyse einer Differentialgleichung - Richtungsfeld
Wir betrachten eine Differentialgleichung erster Ordnung y f (x, y) .
Die Funktion y(x) sei eine Lösung dieser Gleichung und der Graph von y(x) gehe durch den
Punkt (x0 , y0 ) .
Die Steigung der Tangente an die Funktion y(x) in diesem Punkt beträgt y (x0 ) . Dies ist aber
f (x0 ,y0 ) , die rechte Seite der obigen Differentialgleichung y f (x, y) .
Um zu verstehen, wie der Graph der Funktion verläuft, zeichnet man kurze
Tangentenstückchen mit den entsprechenden Steigungen in ein Koordinatensystem. Die
entstehende Graphik nennt man Richtungsfeld einer Differentialgleichung erster Ordnung.
Mit Hilfe des Richtungsfeldes versteht man auch, was mit der Lösung der
Differentialgleichung in verschiedenen Bereichen des Koordinatensystems geschieht.
Die Lösung der Differentialgleichung wächst, falls die Steigung positiv ist,
die Lösung der Differentialgleichung nimmt ab, falls die Steigung negativ ist und
die Lösung der Differentialgleichung verläuft parallel zur x-Achse, falls die Steigung 0 ist.
Beispiel:
Gegeben sei die Differentialgleichung 1. Ordnung
Gesucht ist das Richtungsfeld.
Zeichnet man nun dieses
Richtungsfeld, so lassen sich
die Lösungskurven von Hand
in das Richtungsfeld
einpassen.
y' = x
gsa ve cu rrentp oint tran slate stro
1 4 ke
4
di v1setl
4 di
inewid
v setlth
inewid
0 sthetgra0ys etgra
0.0 00
stro
220
.870
ke
y 2220
114
149
6.1
00.0
164
12
.565
.000
.870
00
.565
2 62.2
m164
201
235
oveto
moveto
75
.000
.435
.565
m ove
mo
4.0
30
5
Es wird etwas parabelartiges
herauskommen.
Am Richtungsfeld ist deutlich
zu sehen, dass es keine
eindeutige Lösung gibt,
solange nicht noch gewisse
Anfangsbedingungen gegeben
sind.
-5
Man könnte beispielsweise
verlangen, dass die gesuchte
Kurve durch einen
bestimmten Punkt, wie in der
nebenstehenden Skizze durch P(2/1), gehen muss.
Dadurch wird aus der Schar von Lösungskurven genau eine ausgewählt.
P