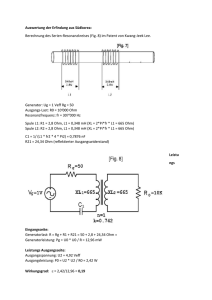
BWB-2_2012-Loesungen Experiment

31. ÖSTERREICHISCHE PHYSIK-OLYMPIADE-2012
Bundeswettbewerb - 2. Teil
Eisenstadt, 29.Mai – 13.Juni 2012
Experimentelle Aufgabe aus ELEKTRIZITÄT
Heimo HERGAN
BORG 8020 Graz Dreierschützengasse 15
Lösungsvorschläge
Feldverteilung und galvanische Elemente
2
1
1
1. Feldverteilungen
a. Die Elektroden werden laut Bild montiert, Wasser eingefüllt (wirkt dann wie ein
Potentiometer), die Elektroden mit der Batterie kontaktiert. Das Voltmeter lässt sich
direkt als Indikator für die Äquipotentiallinien verwenden (ein Anschluss an der
Elektrode, einer im Wasser zur Suche des Punktes mit der entsprechenden gesuchten
Potentialdifferenz. Die Punkte gleichen Potentials lassen sich verbinden und bilden so
die Äquipotentiallinien. Senkrecht dazu – ausgehend und endend bei den Elektroden –
kann man die Feldlinien einzeichen. (Da die Gesamtspannung ca. 4,6V beträgt, sind die
Potentialdifferenzen zwischen benachbarten Äquipotentiallinien laut Messvorgabe in
Volt 1-1-1,6-1-1). Die erste Potentiallinie liegt jeweils erstaunlich knapp neben der
jeweiligen Elektrode und verläuft in der Nähe einer Elektrodenspitze deutlich dichter an
der nächsten.
Die Feldstärke lässt sich zunächst über die Feldlinienlage und -dichte abschätzen und
U
 E numerisch ermitteln. Dazu misst man den Abstand zwischen 2
über
x
benachbarten Äquipotentiallinien entlang der dazu senkrecht eingezeichneten
Feldlinien x und liest die Potentialdifferenz U aus der Messskizze ab. Die
gemessenen Feldstärken liegen zwischen weniger als 100 V/m und mehreren 100 V/m.
U
dQ
ergibt den Widerstand, mit I 
und Q  n  e erhält man die Zahl der
I
dt
bewegten Ladungen, über die Wertigkeit der Ionen deren Zahl. Bei 4,6V Spannung und
wenigen mA Stromstärke liegt der Widerstand bei 1 bis 2 k - je nach Anordnung.
A
c. R aus b) und   R  ergibt den spezifischen Widerstand des verwendeten
l
Leitungswassers, weil die Elektroden viel besser leiten. Mit rund 15 cm 2 Fläche und
mS
10cm Abstand ergibt das eine spezifische Leitfähigkeit von 30 bis 50
.
m
b. R 
1
31. ÖSTERREICHISCHE PHYSIK-OLYMPIADE-2012
Bundeswettbewerb - 2. Teil
Eisenstadt, 29.Mai – 13.Juni 2012
Experimentelle Aufgabe aus ELEKTRIZITÄT
Heimo HERGAN
BORG 8020 Graz Dreierschützengasse 15
Lösungsvorschläge
3
2. Spannungsreihe, galvanische Elemente
a. Die Metalle müssen zunächst in einem Elektrolyten paarweise miteinander verglichen
werden. Dabei ist darauf zu achten, dass die Polung des Messgeräts immer gleich bleibt.
Cu
2cm Abstand
1cm breit
+\- mV Cu Me Pb Fe zn
Fe/Zn Niro Al
Cu
0 61 379 392 808
784
-76 430
Me
-38
0 313 138 754
666
-80 290
Pb
-389 -355
0 -280 270
280 -430
80
Fe
-380 -365 -118
0 216
203 -470
-90
Zn
-812 -810 -565 -720
0 -235 -902 -480
Fe/Zn
-770 -744 -490 -667 -139
0 -816 -440
Niro
70 100 360 160 686
626
0 420
Al
-360 -306 -33 -220 272
230 -311
0
Platz
Cu
Me
Pb
Fe
Zn
Fe/Zn
Niro
Al
Zahl
1
2
3
4
5
6
7
8
Niro Cu Me Pb Fe
Al
Fe/Zn Zn
Niro Cu Me Fe Al
Pb
Fe/Zn Zn
Niro Cu Me Fe Pb
Al
Zn
Fe/Zn
Niro Cu Me Pb Fe
Al
Fe/Zn Zn
Niro Cu Me Fe Pb
Al
Fe/Zn Zn
Niro Cu Me Fe Pb
Al
Zn
Fe/Zn
Niro Cu Me Fe Pb
Al
Fe/Zn Zn
Cu Niro Me Fe Pb
Al
Fe/Zn Zn
7/1 7/1
8 6/2 5/2/1 7/1
6/2
6/2
Erdapfel,
d  2 cm ,
b  2 cm
anschließend sortiert
man die Messwerte
absteigend und erhält
eine – in einigen
Bereichen nicht
übereinstimmende –
Reihung mit
entsprechender
Häufigkeit.
Gegebenenfalls muss mit anderen Elektrolyten eine Gegenprobe erfolgen. Im
Wesentlichen wird aber die Reihung bestätigt.
2
31. ÖSTERREICHISCHE PHYSIK-OLYMPIADE-2012
Bundeswettbewerb - 2. Teil
Eisenstadt, 29.Mai – 13.Juni 2012
Experimentelle Aufgabe aus ELEKTRIZITÄT
Heimo HERGAN
BORG 8020 Graz Dreierschützengasse 15
Lösungsvorschläge
3
b. Aus den in den Tabellen dargestellten Messwerten sieht man, dass Nirosta (und darüber
hinaus der Kohlenstoff in Form einer Graphitmine) in der „Spannungsreihe“ ganz links (ganz
oben) liegen, dicht gefolgt vom Kupfer. Ganz rechts (ganz unter) ist Zink. Chemisch gesehen
wäre Kohlenstoff am edelsten und Zink am unedelsten.
Niro/Zn
U_0 (mV)
U_Kl (mV)
Erdapfel I_K (µA)
R_i (Ohm)
rho (Ohm.m)
U_0 (mV)
U_Kl (mV)
Apfel I_K (µA)
R_i (Ohm)
rho (Ohm.m)
U_0 (mV)
U_Kl (mV)
Zitrone I_K (µA)
R_i (Ohm)
rho (Ohm.m)
2qcm 4qcm
972 960
40
60
360 550
2589 1636
51,8 65,5
1080 1020
22
30
200 260
5290 3808
106 152
1049 1048
102 210
314 500
3016 1676
60,3
67
Cu/Zn
2qcm 4qcm
U_0 (mV)
940 960
U_Kl (mV)
50
60
Erdapfel I_K (µA)
380 618
R_i (Ohm)
2342 1456
rho (Ohm.m) 93,7 58,3
U_0 (mV)
960 960
U_Kl (mV)
26
32
Apfel I_K (µA)
238 284
R_i (Ohm)
3924 3268
rho (Ohm.m) 157 131
U_0 (mV)
907
U_Kl (mV)
40
Zitrone I_K (µA)
350
R_i (Ohm)
2477
rho (Ohm.m)
99,1
Man sieht, dass der Elektrolyt auf die Spannung
wenig Einfluss hat, wohl aber auf den
Kurzschlussstrom, ebenso wie die Elektrodenfläche.
So lassen sich auch die sehr kleinen
Kurzschlussströme bei den verschiedenen
Graphitminen erklären.
Während die Innenwiderstände von Abstand und
Fläche erwartungsgemäß abhängen, zeigt der
spezifische Widerstand ebenso erwartungsgemäß
wenig Unterschied beim gleichen Elektrolyten, wohl
aber bei verschiedenen. So zeigt Apfel (grüner
Niro U_0 U_Kl I_K
Golden Delicious) in beiden Fällen einen größeren
Erdapfel C/B
-240
-1 -2
Innenwiderstand als Zitrone oder Kartoffel. Bei der
C/HB -400
-1 -5
Zitrone dürfte die Säure dafür sorgen, bei der
Kartoffel die sehr gleichmäßige Zellstruktur und der leicht saure pH-Wert.
C/B
Zn
Erdapfel Cu
Niro
Zn
Apfel Cu
Niro
Zn
Zitrone Cu
Niro
U_0 U_Kl I_K
1000
0 1
206
0 2
240
1 2
960
6 44
170
0 1
270
0 2
870 10 72
70
0 1
112
0 2
3