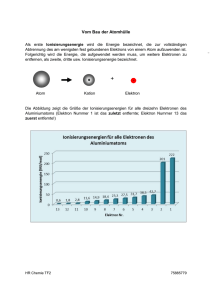
4 0,0000 0,0000 1,0000 0,0000

Skript zum Seminarthema:
Erstellungskonzept eines Programms zur
Durchführung von HÜCKEL-Rechnungen
zum Einsatz in der Lehre
Erster Betreuer:
Prof. Dr. Horst Schäfer
Zweiter Betreuer:
Prof. Dr. Gerhard Raabe
Erstellt von:
Daniel Dautaj
1
Inhalt
Erich Hückel ............................................................................................................................................. 3
Einleitung ............................................................................................................................................. 4
Grundlagen der Quantenmechanik ......................................................................................................... 4
Der Welle-Teilchen-Dualismus der Materie ........................................................................................ 5
Das Unbestimmtheitsprinzip ............................................................................................................... 6
Das Elektron im Kasten.................................................................................................................... 6
Chemische Bindungen ............................................................................................................................. 9
Orbitale ................................................................................................................................................ 9
Die σ-Bindung ...................................................................................................................................... 9
Die π-Bindung.................................................................................................................................... 10
Theoretische Grundlagen des HÜCKEL-Verfahrens............................................................................... 11
Die Separierbarkeit von 𝝅-Elektronen und 𝝈-Elektronen ................................................................. 11
Die Matrixelemente des HÜCKEL-Operators..................................................................................... 14
Die Umsetzung ...................................................................................................................................... 20
Input-File ........................................................................................................................................... 20
Output-File ........................................................................................................................................ 21
Quellenangaben: ................................................................................................................................... 25
2
Erich
Armand
Arthur
Joseph
Hückel
Bild: Erich Hückel
(Wikipedia)
Erich Hückel wurde am 06.08.1896 als Sohn von Marie und Armand Hückel in Berlin
geboren. Er hatte zwei Brüder, Rudi und Walter. Walter machte sich später als
Ordinarius für Organische Chemie einen Namen. Erich Hückel studierte Mathematik
und Physik in Göttingen und gilt als eine der großen Persönlichkeiten der
Quantenchemie.
Erich Hückel fertigte seine Dissertation auf experimenteller Basis über Streuung von
Röntgenstrahlen bei Peter Debye an. Danach arbeitete er zwei Jahre lang als
Mathematikassistent und wechselte anschließend an die Eidgenössischen
Technischen Hochschule nach Zürich, wo er an der Debye-Hückel-Theorie arbeitete.
Es ist leider nicht ganz klar, wer den größeren Beitrag zur dieser Theorie geleistet hat.
Aber Hückel investierte seine Zeit schon in dieser frühen Phase seines Lebens in noch
offene Fragen auf dem Gebiet der Physikalischen und Organischen Chemie. Hier
entwickelte er entsprechende Theorien, die auf sehr pragmatischen Verfahren
basierten. Auf der Grundlage einfacher Annahmen fand er Wege die schließlich nicht
nur zu plausiblen Erklärungen führten, sondern auch zu überprüfbaren Voraussagen.
Später bei Donnan in London vollendete er seine vermutlich wichtigste Arbeit,
nämlich die auf dem Gebiet der organischen Quantenchemie. Im Jahr 1930 arbeitete
er als Dozent an der Technischen Hochschule in Stuttgart und sieben Jahre später
wurde er auf eine Professur in Marburg berufen. Hier beschäftigte er sich mit der
quantenmechanischen Beschreibung ungesättigter und konjugierter Moleküle, die
insbesondere auf dem Gebiet der Farbstoffchemie eine wichtige Rolle spielten (und
immer noch spielen). Obwohl er Theoretiker war, versuchte er seine Theorie im
Rahmen starker approximativer Methoden einfach darzustellen, wie z.B. im Fall
cyclischer Moleküle. Weiterhin beschäftigte er sich mit der Bedeutung der
3
Konnektivität der Atome für die Spinmultiplizität was später die Grundlage für die
Hundsche Regel bildete. Die moderne Organische und Physikalische Chemie basiert
heute zu einem nicht unwesentlichen Teil auf den von Erich Hückel erarbeiteten
Methoden und Theorien, wie z.B. der Hückel-Molekularorbitaltheorie, der Theorie
der Elektrolyte oder der quantentheoretischen Deutung der thermodynamischen
Eigenschaften des Benzols.
Erich Hückel wurde 1965 der Otto-Hahn-Preis für Chemie und Physik verliehen.
Einleitung
Um das Erstellungskonzept des Programms zur Durchführung von HÜCKELRechnungen zu realisieren, sollte man sich einen Überblick über die Grundlagen der
HÜCKEL-Theorie verschaffen. Diese basiert auf der Theorie der chemischen Bindung
und setzt daher notwendigerweise Kenntnisse der Physik voraus. Da bei der
Beschreibung atomarer Vorgänge die klassische Physik versagt, muss man sich
zunächst einen Überblick über das in diesem Zusammenhang wichtigste Teilgebiet
der Physik, nämlich das der quantenmechanischen Vorgänge verschaffen.
Hierauf kann in diesem Zusammenhang nicht genauer eingegangen werden, da dies
über den Rahmen der Seminararbeit hinausgehen würde.
Grundlagen der Quantenmechanik
Durch die Einführung der der auf der Planckschen Quantentheorie beruhenden
Bohrschen Postulate stellte Niels Bohr das ursprünglich von Ernest Rutherford
erarbeitete Modell zur Bewegung der Elektronen auf kreisförmigen Bahnen um den
Atomkern eine neue Grundlage. Die aus den Bohrschen Vorstellungen folgenden
diskreten Energiezustände der Elektronen in einem Atom wurden später von Franck
und Hertz durch Elektronenstoßexperimente gestützt.
Später versuchte Sommerfeld, die Bohrschen Vorstellungen des Atommodells zu
erweitern, indem er für die Elektronen nicht nur kreisförmige sondern auch
elliptische Bewegungen einführte. Im Fall des Heliumspektrums versagte die Theorie
schließlich. Damit zeigte sich, dass die aus makroskopischen Erscheinungen
gewonnen Anschauungen, wie z.B. Kreisbahnen, im atomaren Bereich keine
Gültigkeit mehr besitzen. Anders formuliert versagen die Gesetze der klassischen
Physik im atomaren Bereich vollständig und besitzen dort keine Gültigkeit mehr.
Die Aufgabe der grundlegenden klassischen Vorstellungen war der Anfang der
modernen Quantentheorie.
4
Der Welle-Teilchen-Dualismus der Materie
Je nach durchgeführtem Experiment kann Licht entweder als aus Teilchen bestehend
oder aber als eine elektromagnetische Wellenerscheinung interpretiert werden. Licht
breitet sich im Vakuum mit der konstanten Geschwindigkeit
𝑐 = 2,998 ∙ 1010 𝑐𝑚 𝑠 −1
aus. Die Geschwindigkeit ist proportional zur Frequenz ν und der Wellenlänge λ:
𝑐 =𝜈∙𝜆
Der Wellencharakter des Lichts kann durch Beugungsexperimente gezeigt werden.
Die Interpretation des Lichtes als Strom von Photonen, liegt der Erklärung des
photoelektrischen Effekts von Einstein (1905) zu Grunde. Wenn mit Licht eine
Metallplatte aus Cäsium bestrahlt wird, werden Elektronen des Metalls aus der
Plattenoberfläche freigesetzt („Photoelektronen“).
Durch Erhöhung der Lichtintensität wird dabei die Anzahl der freigesetzten
Elektronen erhöht, ihre Energie aber nicht verändert.
𝐸 = ℎ𝜈
(ℎ = 6,626 ∙ 10−34 J s ist bekannt als Plancksche Konstante oder Plancksches
Wirkungsquantum)
In diesem Teilabschnitt der Quantenmechanik wurde gezeigt, dass Teilchen je nach
durchgeführtem Experiment Welleneigenschaften oder Teilcheneigenschaften
zeigen. Der Welle-Teilchen Dualismus erfordert eine neue Theorie, die im Rahmen
der Quantenmechanik beschrieben wird. Ein Teilchen kann man leicht als ein Punkt
im Raum mit den entsprechenden Koordinaten lokalisieren. Im Gegenteil dazu lässt
sich aber für eine Welle nur ihre Amplitude an einer Stelle des Raumes angeben und
das führt uns zum nächsten Thema.
5
Das Unbestimmtheitsprinzip
Das Elektron im Kasten
Elektron in einem eindimensionalen Kasten
Als ein einführendes Beispiel im Rahmen der angewandten Quantentheorie bietet
sich die Behandlung eines Teilchens (in unserem Fall ein negativ geladenes Teilchen,
ein Elektron) mit der Masse m an, das sich in einem eindimensionalen Kasten entlang
der x-Achse zwischen 0 und a bewegt.
Dazu könnte man sich als klassisches Analogon die Bewegung einer Billardkugel auf
einem Billardtisch vorstellen. Mit der Restriktion, dass sich die Billardkugel zwischen
zwei Banden im Abstand a geradlinig und eindimensional bewegt. Dabei muss
außerdem beachtet werden, dass die Reflexion der Kugel immer senkrecht zu den
Tischbanden erfolgt.
Als weitere Randbedingung soll im Bereich zwischen x = 0 und x = a das Potential
verschwinden, d.h. dass auf das Elektron in diesem Bereich keine Kräfte wirken. Im
Gegenteil dazu ist das Potential sowohl bei x = 0 als auch bei x = a unendlich groß. Als
Folge wird das Elektron an diesen Grenzen durch unendlich große Kräfte in den
Kasten zurückgetrieben. Außerhalb des Kastens kann man das Elektron demnach
nicht antreffen.
In der klassischen Physik wird die Gesamtenergie eines Teilchens in Form der
Hamiltonfunktion (H = T + V) angegeben.
Wobei T die klassische kinetische Energie und V die klassische potentielle Energie ist.
Die kinetische Energie ist eine Funktion des Impulses und die potentielle Energie eine
Funktion der entsprechenden Ortskoordinaten (z.B.: 𝑝𝑥 , 𝑥). Aufgrund der
Heisenbergschen Unschärferelation besitzen atomare Teilchen nicht gleichzeitig
scharfe Werte für Ort und Impuls. Daher müssen die klassischen Ausdrücke für die
6
kinetische Energie (T) und die potentielle Energie (V) durch die entsprechenden
Operatoren T und V ersetzt werden. Die Summe dieser Operatoren bezeichnet man
als Hamilton-Operator ℋ:
𝓗ℋ = 𝑻 + 𝑽
Wenn man von der Schrödinger-Gleichung unter Einsatz des Hamilton-Operators
ausgeht
ℋφ = Eφ
erhält man die Eigenwertgleichung der Energie
𝑻
𝑽
⏞ ћ2 𝜕 2
𝜕2
𝜕2
⏞
−
(
+
+
) + 𝑉(𝑥, 𝑦, 𝑧) 𝜑(𝑥, 𝑦, 𝑧) = 𝐸𝜑(𝑥, 𝑦, 𝑧)
2𝑚 𝜕𝑥 2 𝜕𝑦 2 𝜕𝑧 2
[
]
Die Funktion
𝜑(𝑥, 𝑦, 𝑧)
bezeichnet man als Wellenfunktion des betrachteten Systems.
Da sich unser Elektron nur in der x-Richtung bewegt, lautet die
Schrödinger-Gleichung für das Elektron im eindimensionalen Kasten wie folgt:
−
ћ2 𝑑2
𝜑(𝑥) = 𝐸𝜑(𝑥)
2𝑚 𝑑𝑥 2
Die Lösung dieser Gleichung liefert die Energieeigenwerte und die normierbaren
Eigenfunktionen für ein Elektron im Kasten. Eine Lösung ist z.B. eine Sinusfunktion
A·sin(Bx) an, da zweimaliges Differenzieren wieder zur gleichen Sinusfunktion führt.
Als Ergebnis der Rechnung wird folgende Gleichung erhalten:
2
𝜋𝑛
𝜑𝑛 (𝑥) = √𝑎 sin ( 𝑎 𝑥)
Für die zugehörigen Energien erhält man:
𝐸𝑛 =
ℎ2
8𝑚𝑎2
𝑛2 mit n = 1,2,3….
Man kann die Richtigkeit dieser Gleichung zeigen, indem man den angegebenen
Ausdruck für φn in die entsprechende Schrödinger-Gleichung einsetzt. Außerdem
kann man leicht zeigen, dass für φn die Normierungsbedingung erfüllt ist.
7
Es gilt:
𝑎 𝑎 2 𝜋𝑛
∫ 𝑠𝑖𝑛 ( 𝑥) 𝑑𝑥 = 1
2 0
𝑎
Wir entnehmen der Energiegleichung, dass eine diskrete Folge von
Energieeigenwerten 𝐸1 = (ℎ2 ⁄8𝑚𝑎2 ), 𝐸2 = (ℎ2 ⁄8𝑚𝑎2 ) 4, … auftritt. Das
betrachtete System befindet sich nur in solchen Zuständen, die durch die
angegebenen Energiewerte charakterisiert sind. Im klassischen Fall könnte sich das
Elektron mit jeder beliebigen Energie bewegen, die Quantenmechanik zeigt hingegen,
dass man bei Messungen an diesem hypothetischen System für die Energie nur die
angegebenen ganzzahligen Vielfachen von
ℎ2 ⁄8𝑚𝑎2
erhält. Es tritt somit eine „Quantelung“ der Energie auf. Die möglichen Zustände 𝜑𝑛
und die zugehörigen Energieeigenwerte En werden durch die verschiedenen Werte
der Quantenzahl n∈N festgelegt.
Die Quantenmechanik beschränkt die Werte der Energie, wobei der niedrigste
mögliche Energieeigenwert nicht E = 0, sondern E = E1 ist. Den Zustand mit dem
niedrigsten Energieeigenwert (also den Zustand φ1 ) nennt man den Grundzustand
des Systems.
Bild: Die vier niedrigsten Energieeigenwerte und die zugehörigen Wellenfunktionen für ein Elektron in einem
eindimensionalen Kasten der Länge a
8
Chemische Bindungen
Orbitale
Bevor auf die chemischen Bindungen eingegangen wird, wird kurz der Begriff des
„Orbitals“ erklärt. Ein Orbital ist eine Funktion (im Idealfall eine Eigenfunktion des
enstprechenden Hamiltonsoperators), die Elektronen eines Atoms (Atomorbital) oder
eines Moleküls (Molekülorbital) beschreibt. Das Betragsquadrat eines Orbitals an
einer Stelle des Raumes gibt die Wahrscheinlichkeitsdichte für den Aufenthalt eines
Elektrons an dieser Stelle des Raumes an. Im Fall von Atomen gibt es z.B.: s, p, d, f
Orbitale.
Das energieärmste ist das s-Orbital, gefolgt von p, d, … wobei außerdem beachtet
werden muss, dass energiegleiche (entartete) Orbitale zunächst einfach, mit
Elektronen gleichen Spins besetzt werden (Hundsche Regel). Nach dem Pauli Prinzip
können die Orbitale mit maximal zwei Elektronen entgegengesetzten Spins besetzt
werden.
In dieser Arbeit werden die s- und p- Orbitale näher betrachtet, wobei der gefüllte
Teil, ein positives Vorzeichen und der nicht gefüllte, ein negatives Vorzeichen des
Orbitals symbolisiert.
Im Fall der p-Orbitale kann man Funktionen definieren, die entlang der Achsen der
entsprechenden Raumkoordinaten orientiert sind. Das sind die 𝑝𝑥 , 𝑝𝑦 , 𝑝𝑧 Orbitale.
Die σ-Bindung
Einer σ-Bindung liegt ein bindendes σ-Molekülorbital zugrunde, das durch
verschiedene Überlappungsmöglichkeiten der s- und p-Orbitale gebildet werden
kann.
9
𝛔-Bindung im einen Ethen-Molekül
Die π-Bindung
Man bezeichnet Bindungen, die bei der Überlappung von 2 p-Orbitalen entstehen
und parallel zur Knotenebene ausgerichtet sind, als π-Bindungen. Die
entsprechenden Orbitale nennt man  Orbitale.
10
-Bindung in C2H4
H
H
C
C
H
H
-Bindung in C2H4
𝛑-Bindungen im Ethen-Molekül
Theoretische Grundlagen des HÜCKEL-Verfahrens
Die Separierbarkeit von 𝝅-Elektronen und 𝝈-Elektronen
Im Rahmen der einfachen HÜCKEL-Theorie werden 𝜋-Elektronensysteme berechnet,
ohne die gleichzeitige Gegenwart von 𝜎-Elektronen explizit zu berücksichtigen. Um
an dieser Stelle Missverständnisse zu vermeiden, sei ausdrücklich darauf
hingewiesen, dass die Betonung auf „explizit“ liegt.
Separierbarkeit bedeutet hier nicht, dass die 𝜋-Elektronen die gleichzeitige
Anwesenheit von 𝜎-Elektronen (und umgekehrt) überhaupt nicht „spüren“, sondern
dass man die Wechselwirkung der 𝜋-Elektronen mit den 𝜎-Elektronen in Form eines
effektiven Operators der potentiellen Energie 𝑉𝑒𝑓𝑓 berücksichtigt.
Dieser Vorstellung zufolge bildet das Gerüst der 𝜎-Elektronen zusammen mit den
Kernen ein effektives Feld, in dem sich die 𝜋-Elektronen bewegen. Man nimmt nun
weiterhin an, dass sich auch die Wechselwirkungen der Elektronen in 𝜋-Orbitalen
untereinander mit in diesen effektiven Operator hineinstecken lassen. Jedes 𝜋Elektron bewegt sich demnach in einem effektiven Feld, welches einerseits durch das
𝜎 gebundene Molekülgerüst und andererseits durch die restlichen 𝜋-Elektronen
erzeugt wird.
Der Hamiltonoperator ℋ für ein System aus n 𝜋-Elektronen lautet dann:
11
1
ℋ(1,2, … 𝑛) = Σni=1 (− Δ(i) + 𝑉𝑒𝑓𝑓 (i)) = Σni=1 ℋ(𝑖)
2
Er besteht also aus einer Summe von n Einelektronoperatoren (ℋ(𝑗)).
Legt man diese Vorstellungen zugrunde, dann kann man leicht zeigen, dass die
Matrixelemente des Operators ℋ zwischen π- und σ-Funktionen
+∞
∫
𝜑 𝜎 (𝑖)ℋ(𝑖)𝜑 𝜋 (𝑖)𝑑𝜏
−∞
unter der Voraussetzung einer strengen Planarität des π-Systems den Wert Null
annehmen.
Tauscht man in ℋ(𝑗)
1
ℋ(𝑗) = − ∆(𝑗) + 𝑉𝑒𝑓𝑓 (𝑗)
2
𝑥𝑗 , 𝑦𝑗 und 𝑧𝑗 gegen 𝑥𝑗 , 𝑦𝑗 und −𝑧𝑗 aus d.h. spiegelt man an der Molekülebene
Molekülebene
So ändert man an dem Operator der kinetischen Energie
𝜕2
𝜕2
𝜕2
∆(𝑗) = 2 +
+
𝜕𝑥𝑗
𝜕𝑦𝑗2 𝜕𝑧𝑗2
nichts.
Ähnlich leicht verständlich ist, dass 𝑉𝑒𝑓𝑓 (𝑗) in gleichen Abständen oberhalb
(+𝑥𝑗 , +𝑦𝑗 , −𝑧𝑗 ) der Molekülebene gleich sein muss.
12
Bei einer 2𝑝𝑧 -Funktion kehrt sich bei der Spiegelung an der Molekülebene das
Vorzeichen um. Da aber ℋ(𝑗) in einem Punkt oberhalb und dem gespiegelten Punkt
unterhalb der Molekülebene gleich ist ergibt
ℋ(𝑗)𝜑𝜋 (𝑗)
eine Funktion, die ebenfalls bei der Spiegelung an der Molekülebene (d.h. bei Ersatz
von (𝑥𝑗 , 𝑦𝑗 , 𝑧𝑗 ) durch (𝑥𝑗 , 𝑦𝑗 , −𝑧𝑗 )) ihr Vorzeichen wechselt. Multipliziert man nun noch
die Funktion
ℋ(𝑗)𝜑𝜋 (𝑗)
mit der 𝜎-Funktion 𝜑𝑗𝜎 , die oberhalb und unterhalb der Molekülebene das gleiche
Vorzeichen hat, so besitzen diese Produkte oberhalb und unterhalb in gleichen
Abständen von der Molekülebene die gleichen Beträge bei unterschiedlichen
Vorzeichen.
Summiert man über alle Produkte (d.h. führt man die Integration aus), so ergibt sich:
+∞
𝜑 𝜎 (𝑗)ℋ(𝑗)𝜑 𝜋 (𝑗) 𝑑𝑡𝑗 = 0
∫
−∞
Bei der Bildung des Energieerwartungswertes
+∞
Ε𝜙𝑗′ =
′
∫−∞ ∅∗𝑗 ℋ ∅𝑗 𝑑𝑡
+∞
′
∫−∞ ∅𝑗∗ ∅𝑗 𝑑𝑡
unter Verwendung einer Linearkombination
𝑛
∅′𝑗
= ∑ 𝑐𝑖𝑗 𝜑𝑖
𝑖=1
bei der i=1…m die Atomfunktionen mit π-Symmetrie und i=m…n die Atomfunktionen
mit σ-Symmetrie beschrieben, so erhält man eine geblockte Säkulardeterminante in
der der eine Block das π- und der andere Block das σ-System beschreibt.
𝐻11 − Ε
𝐻12
⋯
𝐻1𝑚
𝐻21
𝐻22 − Ε ⋯
𝐻2𝑚
| ⋮
⋮
⋱
⋮
𝐻𝑚1
𝐻𝑚2
⋯ 𝐻𝑚𝑚 − Ε
|
|
0
0
|
𝐻𝑚+1,𝑚+1 − Ε
𝐻𝑚+1,𝑚+2
⋯ 𝐻𝑚+1,𝑛 | = 0
𝐻𝑚+2,𝑚+1
𝐻𝑚+2,𝑚+2 − Ε ⋯ 𝐻𝑚+2,𝑛
|
⋮
⋮
⋱
⋮
𝐻𝑛,𝑚+1
𝐻𝑚,𝑚+2
⋯ 𝐻𝑛,𝑛 − Ε
13
Dieser Block der oberen Determinante beschreibt das σ-System.
𝐻𝑚+1,𝑚+1 − Ε
𝐻𝑚+2,𝑚+1
|
⋮
𝐻𝑛,𝑚+1
𝐻𝑚+1,𝑚+2
𝐻𝑚+2,𝑚+2 − Ε
⋮
𝐻𝑚,𝑚+2
⋯ 𝐻𝑚+1,𝑛
⋯ 𝐻𝑚+2,𝑛
|=0
⋱
⋮
⋯ 𝐻𝑛,𝑛 − Ε
Was wir nun im Folgenden betrachten werden, ist die Determinante
𝐻11 − Ε
𝐻12
𝐻21
𝐻22 − Ε
|
⋮
⋮
𝐻𝑚1
𝐻𝑚2
⋯
𝐻1𝑚
⋯
𝐻2𝑚
|=0
⋱
⋮
⋯ 𝐻𝑚𝑚 − Ε
die das π-System beschreibt.
Die Matrixelemente des HÜCKEL-Operators
In der HÜCKEL-Theorie gibt man weder für die Funktionen, noch für den HÜCKELOperator einen analytischen Ausdruck an, sondern definiert beide Größen über ihre
Eigenschaften oder besser gesagt in ihrer Wirkung aufeinander. Die in dem LCAOAnsatz für die HÜCKEL-Molekülorbitale verwendeten Funktionen 𝜑𝜇 , besitzen das
gleiche Symmetrieverhalten wie 2𝑝𝑧 - Funktionen und sind orthonormiert
+∞
𝜑𝜇∗ 𝜑𝜇 𝑑𝜏 = 1
∫
−∞
+∞
∫
𝜑𝜇∗ 𝜑𝜗 𝑑𝜏 = 1
−∞
oder bildlich dargestellt:
Dies zeigt den Unterschied zu den 2𝑝𝑧 - Funktionen an zwei benachbarten Zentren.
Zwischen solchen Funktionen besteht eine, wenn auch kleine Überlappung:
14
+∞
𝑆𝜇𝜈 = ∫
−∞
2𝑝𝑧𝜇 2𝑝𝑧𝜗 𝑑𝜏
Die Annahme:
+∞
∫
𝜑𝜇 𝜑𝜗 𝑑𝜏 = 𝛿𝜇𝜗
−∞
darf auf keinen Fall mit der Orthogonalitätsbedingung verwechselt werden, die für
die an einem Zentrum lokalisierten Eigenfunktionen eines Operators mit
verschiedenen Eigenwerten gilt.
Die HÜCKEL-Molekülorbitale Ψ𝑖 , die man als Linearkombination dieser Funktionen
ansetzt
𝑛
Ψ𝑖 = ∑ 𝑐𝑖𝜇 𝜑𝜇
𝜇=1
müssen ebenfalls normiert sein, wobei gilt:
+∞
Ψ∗i Ψi dτ = 1
∫
−∞
Unter Berücksichtigung unserer Annahme folgt hieraus
𝑛
2
∑ 𝑐𝜇𝑖
=1
𝜇=1
Der HÜCKEL-Operator
Näherungen)definiert:
wird
durch
die
folgenden
Beziehungen
(HÜCKEL-
Sind die Zentren μ und υ benachbart, dann gibt man dem sogenannten
Resonanzintegral den Wert β (β<0)
+∞
𝐻𝜇𝜐 ≝ ∫−∞ 𝜑𝜇 ℋ𝜑𝜈 𝑑𝜏 = 𝛽 mit β < 0
Sind die Zentren nicht benachbart, dann gibt man dem Resonanzintegral den Wert
Null:
+∞
𝐻𝑢𝑣 ≝ ∫
𝜑𝑢 ℋ𝜑𝑣 𝑑𝜏 = 0
−∞
Dem sogenannten Coulombintegral gibt man den Wert:
+∞
𝐻𝜇𝜇 ≝ ∫
𝜑𝜇 ℋ𝜑𝜇 𝑑𝜏 = 𝛼𝑢
−∞
15
α Entspricht der Energie eines Elektrons in einem 𝑝2 -Orbital, d.h. α < 0.
Die Parameter α und β gewinnt man in der Regel experimentell, z.B. aus
spektroskopischen Daten.
Als Beispiel für die Anwendung des HÜCKEL-Verfahrens soll in der Bachelorarbeit das
π-System der Allyl-Spezies (𝐶𝐻2 − 𝐶𝐻 − 𝐶𝐻2 ) berechnet werden.
In dieser Arbeit wird auf die Hauptpunkte und Ihre Bedeutung eingegangen. Weitere
Details werden in der anschließend durchgeführten Bachelorarbeit bestimmt.
Zuerst setzen nun das HÜCKEL-Molekülorbital als Linearkombination der HÜCKELAtomorbitale an
𝜓 = 𝑐1 𝜑1 + 𝑐2 𝜑2 + 𝑐3 𝜑3
und bildet den Erwartungswert der Energie:
+∞
Ε𝜙 =
∫−∞ 𝜓 ∗ ℋ 𝜓𝑑𝜏
+∞
∫−∞ 𝜓 ∗ 𝜓𝑑𝜏
Wobei die 𝑐𝑖 , 𝑖 = 1,2, … 𝑛
Koeffizienten nach dem LCAO-MO-Ansatz (linear
combination of atomic orbitals for molecular orbitals) bestimmt werden. Wobei das
Prinzip gilt, dass jedes System den Zustand der niedrigsten Energie anstrebt.
Danach nähern wir ϕ an ψ an, in dem wir
𝜕Ε
𝜕𝑐𝑖
bilden.
Später erhalten wir das Säkulargleichungssystem aus dem wir dann die
Säkulardeterminate daraus bilden, die in unseren Fall eine 3x3 Determinante ist.
Aus der Säkulardeterminante lassen sich die
Eigenvektoren berechnen.
Eigenwerte und die zugehörigen
Im Fall des Allylsystems ergeben sich die Eigenwerte:
𝜺𝟏 = 𝜶 + 𝜷√𝟐;
𝜺𝟐 = 𝜶;
𝜺𝟑 = 𝜶 − 𝜷√𝟐;
16
Diese Werte werden in einem Graphen durch die Software „Gnuplotter“ gezeichnet.
Da die Benutzung dieser Software eine gewisse Einarbeitung erfordert wird der
Graph ungefähr so aussehen. Dieser Graph ist mit der Software ChemBioDrawUltra
Version 12 erstellt worden und das MO-Schema (Molecular Orbitals) der Allylsysteme
lässt sich folgendermaßen darstellen:
Bild: MO-Schema der Allylsysteme
Sowohl im Falle des Kations als auch im Falle des Radikals und des Anions ist das
tiefste π-Energieniveau mit zwei Elektronen, deren Spin antiparallel ausgerichtet ist,
besetzt. Beim Kation ist das Niveau bei E = α leer, beim Radikal einfach und beim
Anion doppelt besetzt.
Betrachtet man noch einmal die Abbildung der π-Energieniveaus, dann erkennt man
leicht eine bedeutende Unzulänglichkeit der einfachen HÜCKEL-Theorie: Die Energie
der Elektronen in den besetzten Orbitalen besitzt sowohl im Falle des Radikals als
auch im Falle des Anions unabhängig von der Besetzungszahl (das ist die Anzahl der
Elektronen in einem Molekülorbital) den gleichen Wert.
Man sieht leicht ein, dass die Energie eines π-Elektrons im HOMO (highest occupied
molecular orbital) des Anions höher und damit ungünstiger als im HOMO des Radikals
ist. Die Ursache ist die elektronische Abstoßung zwischen den beiden Elektronen im
HOMO des Anions.
Die Vernachlässigung dieser Abstoßung führt dazu, dass die Elektronenaffinität (das
ist die Energie, die freigesetzt wird, wenn ein Elektron in das energetisch günstigste
nicht vollbesetzte Molekularorbital gebracht wird) der einfachen HÜCKEL-Theorie
zufolge von Allylkation und Allylradikal gleich sind, was mit Sicherheit nicht der
Realität entspricht. Die HÜCKEL-Theorie sollte auf Grund der nur impliziten (d.h. der
17
im Rahmen der Verwendung von α und β) Berücksichtigung der elektronischen
Abstoßung immer dann schlechte Ergebnisse liefern, wenn die Anionen oder stark
polare Moleküle berechnet werden.
Für alternierende Kohlenwasserstoffe mit gleichmäßiger Verteilung der π-Elektronen
sollte man bessere Ergebnisse erhalten als für nicht-alternierende aromatische
Kohlenwasserstoffe. So berechnet man z.B. nach dem einfachen HÜCKEL-Verfahren
für den nicht alternierenden Aromat Azulen
Bild: Nicht alternierender Aromat Azulen
ein Dipolmoment, welches siebenmal so hoch ist wie das experimentell messbare.
Tatsächlich zeigen genauere (und damit aufwendigere) Rechenverfahren, sowie
experimentelle Untersuchungen, dass die Energie für ein π-Elektron im HOMO des
Allylradikals tiefer liegt als die für das Allylanion. Abhilfe von diesem Mangel kann
dadurch geschaffen werden, dass man das Coulombintegral eines Zentrums als
Funktion der Ladung an diesem Zentrum ansetzt. In der sogenannten ω-Technik setzt
man das Coulombintegral des Zentrums x wie folgt an:
𝛼𝑥 = 𝛼0 + (1 − 𝑞𝑥 )𝜔
Wobei 𝑞𝑥 die Ladung des Atoms x ist und ω ein Parameter, der durch Anpassung an
experimentelle Befunde optimiert wird. Hierdurch wird eine bessere
Berücksichtigung der elektronischen Abstoßung ermöglicht. Tatsächlich sind die unter
Verwendung
dieser
Rechentechnik
berechneten
Dipolmomente
für
Kohlenwasserstoffe besser in Übereinstimmung mit dem experimentellen Befund als
die nach dem einfachen HÜCKEL-Verfahren.
Wir haben die π-MO‘s als eine Linearkombination der Atomfunktionen angesetzt:
3
∅i = ∑ 𝑐𝑖𝜇 𝜑𝜇
𝜇=1
Als nächstes sollten die LCAO-Koeffizienten für die π-Molekülarorbitale des
Allylsystems berechnet werden. Bei der Bestimmung des jeweiligen Koeffizienten
sollte man mit der Normierungsbedingung anfangen:
18
𝑐12 + 𝑐22 + 𝑐32 = 1
Zur Berechnung der Koeffizienten muss man die jeweiligen Energieeigenwerte ε in
das Säkulargleichungssystem einsetzen und pro Einsatz im Säkulargleichungssystem
erhält man einen Satz von drei c-Koeffizienten.
Somit erhält man für alle drei Allyl-Spezies für das höchste π-MO
3
1
1
1
∅3 = ∑ 𝑐𝑖𝑗 𝜑𝑖 = 𝜑1 −
𝜑2 + 𝜑3
2
2
√2
𝑖=1
oder bildlich auch dargestellt:
Bild: HOMO des Allyl-Systems
So wie in der unteren Abbildung sollen die Ergebnisse zusammengefasst und
dargestellt werden.
Aus den Werten der umgeformten Säkulardeterminante wird unser Input-ASCII-File
bestehen.
19
Die Umsetzung
Input-File
Wie in der Aufgabenstellung beschrieben, sollte das zu erstellende Programm mit der
Programmiersprache Fortran-90 entwickelt werden. Das Programm sollte ein InputASCII-File einlesen.
Ein Input-File (oder anders genannt als TXT-Datei) wird folgendermaßen aussehen:
1.
Butadien
2.
4
3.
0
4.
1 2 1.0
5.
2 3 1.0
6.
3 4 1.0
7.
1 1 0.0
8.
2 2 0.0
9.
3 3 0.0
10. 4 4 0.0
Die Zeilennummerierung wird kein Bestandteil des Input-Files sein, sondern wurde
hier nur eingeführt damit man die Bedeutung der einzelnen Zeilen besser erklären
kann.
Die erste Zeile zeigt uns, um welches Molekül es sich dabei handelt und in unserem
Fall geht es um das Butadien-Molekül.
Die zweite Zeile zeigt uns die Anzahl der Zentren (N= 4) oder mit anderen Worten
ausgedrückt, gibt sie uns die Anzahl der Kohlenstoffatome an. Daraus kann man
sofort erkennen, dass man im Fall des Butadiens eine 4x4 - Matrix erhält.
Die dritte Zeile zeigt uns die Ladung des Moleküls, die in unserem Fall gleich 0 gesetzt
ist.
Die Ladung des Moleküls wird zur Berechnung der Besetzungszahlen und der
Gesamtenergie verwendet.
Von der vierten bis zur zehnten Zeile werden die meisten Elemente der Matrix
aufgefüllt. Die erste Ziffer entspricht der Zeile der Matrix (i), die zweite Ziffer
entspricht der Spalte der Matrix (j).
Die dritte Zahl entspricht im Fall der Nichtdiagonalelemente dem Resonanzintegral
und im Fall der Diagonalelemente dem Coulombintegral. Die entsprechenden Werte
besetzen die Position (i,j) der Matrix.
20
Von der vierten bis zu sechsten Zeile werden die Elemente der oberen
Nebendiagonale mit dem reellen Wert 1.0 besetzt.
Dieser Wert besitzt laut Aufgabestellung der Bachelorarbeit die Einheit β. Für eine CC-Bindung setzt man in der Regel β=1. Hinsichtlich der Konnektivität der Atome
bedeutet das, dass zwischen den beiden Zentren eine Bindung besteht. Der Wert 1.0
entspricht dem Zahlenwert des Betrags des Resonanzintegrals einer C-C -Bindung.
Von der siebten bis zum zehnten Zeile werden die Elemente der Hauptdiagonalen mit
dem reellen Wert 0.0 aufgefüllt. Dieser Wert entspricht per definitionem dem
Zahlenwert des Coulombintegrals eines Kohlenstoffatoms.
Output-File
Nachdem das Inputfile durch eine Methode eingelesen wurde, sollte eine Matrix die
vorher mit Nullen vorbesetzt wurde, mit den Werten aus den Input-Files aufgefüllt
werden. Anhand einer Spiegelung an der Hauptdiagonalen kann dann die untere
Hauptdiagonale mit den gleichen Werten wie die obere Hauptdiagonale aufgefüllt
werden.
Man erkennt an den Elementen der Matrix ob es sich um ein zyklisches oder
offenkettiges Molekül handelt. Wenn die Anfangs- und Endwerte mit dem reellen
Wert 1.0 besetzt sind, dann handelt es sich um ein geschlossenes zyklisches Molekül,
bei dem Wert 0.0 handelt es sich um ein offenkettiges Molekül.
Danach sollte die Matrix unter Verwendung des Jakobi-Verfahrens diagonalisiert
werden.
Das Jacobi-Verfahren, das auch als Gesamtschritt-Verfahren bezeichnet wird ist ein
lineares, stationäres Iterationsverfahren.
Wenn man ein Gleichungssystem der Form A ∙ x = b, wobei A є R ⁿ*ⁿ, n ϵ N regulär ist
mit direkter Löser die bei exakter Arithmetik nach endlich vielen Schritten die exakte
Lösung x ergibt.
Nachdem die Energieeigenwerte und ihre Eigenvektoren mit den entsprechenden
Methoden berechnet worden sind, sollten diese Ergebnisse in einem Output-ASCIIFile gespeichert werden.
So könnte ein solches Output-File aussehen:
+++++++++++++++++++++++++++++++
HUECKELRECHNUNG FUER BUTADIEN
21
+++++++++++++++++++++++++++++++
**************
HUECKELMATRIX
**************
1
2
3
4
1
0,0000
1,0000
0,0000
0,0000
2
1,0000
0,0000
1,0000
0,0000
3
0,0000
1,0000
0,0000
1,0000
4
0,0000
0,0000
1,0000
0,0000
****************************
EINELEKTRONENENERGIENIVEAUS
****************************
-1,6180
-0,6180
0,6180
1,6180
**********************************
GESAMTENERGIE = ALPHA +4,4721 BETA
**********************************
*******************
KOEFFIZIENTENMATRIX
*******************
1
2
3
4
1
0,3717
-0,6015
-0,6015
-0,3717
2
0,6015
-0,3717
0,3717
0,6015
3
0,6015
0,3717
0,3717
-0,6015
4
0,3717
0,6015
-0,6015
0,3717
22
*************
DICHTEMATRIX
*************
1
2
3
4
1
1,0000
0,8944
0,0000
-0,4472
2
0,8944
1,0000
0,4472
0,0000
3
0,0000
0,4472
1,0000
0,8944
4
-0,4472
0,0000
0,8944
1,0000
**********************
FREIE VALENZ DER ATOME
**********************
1
2
3
4
0,33757
0,39036
0,39036
0,39757
Die Koeffizientenmatrix
Molekülorbitale.
enthält
die
LCAO-Koeffizienten
der
einzelnen
Dabei gibt der Spaltenindex das Molekülorbital und der Zeilenindex das Zentrum im
Molekül an.
1
1
0,3717 (𝑐11 )
2
0,6015(𝑐21 )
3
0,6015(𝑐31 )
4
0,3717(𝑐41 )
2
3
4
∅1 = 0,3717 ∙ φ1 + 0,6015 ∙ φ2 + 0,6015 ∙ φ3 + 0,3717 ∙ φ4
23
Die Bedeutung der DICHTEMATRIX, die oft auch als Bondorder-Matrix bezeichnet
wird, wird deutlich wenn man in den Ausdruck für die Energie eines Molekülorbitals
+∞
∅1∗ ℋ∅1 𝑑𝜏
𝜀1 = ∫
−∞
die LCAO-Entwicklung für ∅1 einsetzt.
𝑛
𝜀1 = ∑
𝑛
∑
𝑘=1
𝑜𝑐𝑐
𝐻𝑘𝑙 ∑
𝑙=1
𝑛𝑖 𝑐𝑘𝑖 𝑐𝑙𝑖
𝑖=1
𝑜𝑐𝑐
𝑝𝑘𝑙 = ∑
𝑛𝑖 𝑐𝑘𝑖 𝑐𝑙𝑖
𝑖=1
𝑝𝑘𝑙 bezeichnet man als einen Element der Dichte- oder Bondordermatrix .
Die Summe der Diagonalelemente 𝑝𝑘𝑘 ist gleich der Zahl der π-Elektronen am
Zentrum k.
𝑛𝑖 ist die Besetzungszahl des i-ten MO’s und occ entspricht der Nummer des
höchstens besetzten MO’s und 𝐻𝑘𝑙 ist das Element der HÜCKEL-Matrix.
Daraus lässt sich dann die Gesamtenergie des π-Systems berechnen.
In diesem Zusammenhang sei darauf hingewiesen, dass man bei alternierenden πElektronensystemen im Grundzustand für alle Diagonalelemente der Dichtematrix
den Wert 1.0 erhält. Die Nicht-Diagonalelemente sind ein Maß für einen
Bindungsgrad zwischen zwei Zentren. An dieser Stelle wäre die Programmierung mit
der Programmiersprache Fortran-90 am Ende.
Wie vorher bereits erwähnt wurde, sollen die Ergebnisse mit einen Plotter-Software
gezeichnet werden. Zur Zeit ist geplant, hierfür die freie Gnu-Plotter-Software zu
verwenden, aber es muss nicht unbedingt dieses Programm benutzt werden, es kann
auch eine andere Software benutzt werden.
Die Benutzung dieses Plotters erfordert eine Einarbeitung in seine
Programmiersprache. Zurzeit wird in Betracht bezogen, dass der Fortran-90-OutputASCII-File von einem nachgeordneten Programm eingelesen wird. In diesem
Programm sollen die Daten aus dem Outputfile in ein für den Plotter „verständliches“
Format umgewandelt werden.
24
So könnte der Energiegraph des Butadien-Moleküls aussehen:
Und so kann eine Strichzeichnung des offenkettigen Moleküls Butadien aussehen:
Quellenangaben:
Zu der hier verarbeiteten Theorie: Vorlesung von Prof. Dr. Gerhard Raabe
G. Raabe, Skript zur Vorlesung „Einführung in die Grundlagen der Theorie der
Chemischen Bindung“ von Prof. Dr. Fleischhauer
25
26