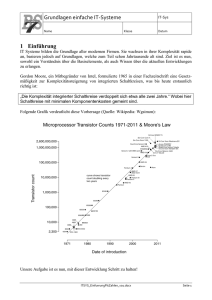
Folien der zweiten Übung(2)
Werbung

Darstellung von rationalen Zahlen Darstellung von 12,5 in Dezimaldarstellung: 1x10 + 2 x10 + 5 x10 1 0 ­1 Binärdarstellung: 1x23 + 1x22 + 0x21 +0x20 + 1x2­1 1100.1 1 Beispiel für Umrechnung 1 0 0 . 1 0 1 1x2 + 0x2 + 0x2 + . 1x2 + 0x2 + 1x2 2 1 0 ­1 ­2 ­3 1x4 + 0x2 + 0x1+ . 1x0.5 + 0x0.25 + 1x0.125 4 + 0 + 0 + . 0.5 + 0 + 0.125 4 . 625 2 Darstellung in mit fester Kommastelle Zweierpotenz 3 2 1 0 ­1 Dezimal Beispiel: 8 4 2 1 0.5 0.25 0.125 0.0625 100.012 0 4 0 0 0 Ergebnis: ­2 ­3 ­4 0.25 0 4,2510 3 Addition von binären Festkommazahlen (8 Bit) Festkomma dezimal 01101001 6.5625 00010100 1.2500 01111101 7.8125 mit 8 Bit sind 2 verschiedene Festkommawerte darstellbar kleinster Wert ≠ 0: 0.0625, der größte Wert: 15.9375 8 4 Umrechnung von dezimal nach binär Beispiel: 7.625 1. Umwandlung des ganzzahligen Teils 2. Umwandlung des gebrochenen Teils dezimal binär Start 0.625 0. ×2 1.250 0.1 .250 0.1 ×2 0.500 0.10 .500 0.10 ×2 1.000 0.101 Ergebnis .000 0.101 5 Stellen Sie 0.110 binäre Festkommazahl dar: ×2 ×2 ×2 ×2 ×2 ×2 ×2 ×2 ×2 ×2 ×2 Ergebnis 0.1 0.2 0.4 0.8 1.6 .6 1.2 0.2 0.4 0.8 1.6 .6 1.2 0.2 0.4 0.8 0. 0.0 0.00 0.000 0.0001 0.0001 0.00011 0.00011 0.000110 0.0001100 0.00011001 0.00011001 0.000110011 0.000110011 0.0001100110 0.00011001100 0.00011001100... 6 Gleitkommazahlen (Floating point) 1.82371 × 10 = 1.82371 × 10 = 18.2371 ­1 1.82371 × 10 = 1.82371 × .1 = .182371 2 1.82371 × 10 = 1.82371 × 100 = 182.371 1.82371 × 10­2 = 1.82371 × .01 = .0182371 1 10n bedeutet: n Positionen nach rechts 10­n bedeutet: n Positionen nach links 7 IEEE­ Format für einfache Genauigkeit 8 Darstellung der Zahl 1.0 0 (für positive), Mantisse: 000 0000 0000 0000 0000 0000 Exponent: 0 Bias: 12710 = 0111 11112 Hexadezimal: 0x3F800000 9