Stationen zur Satzgruppe des Pythagoras

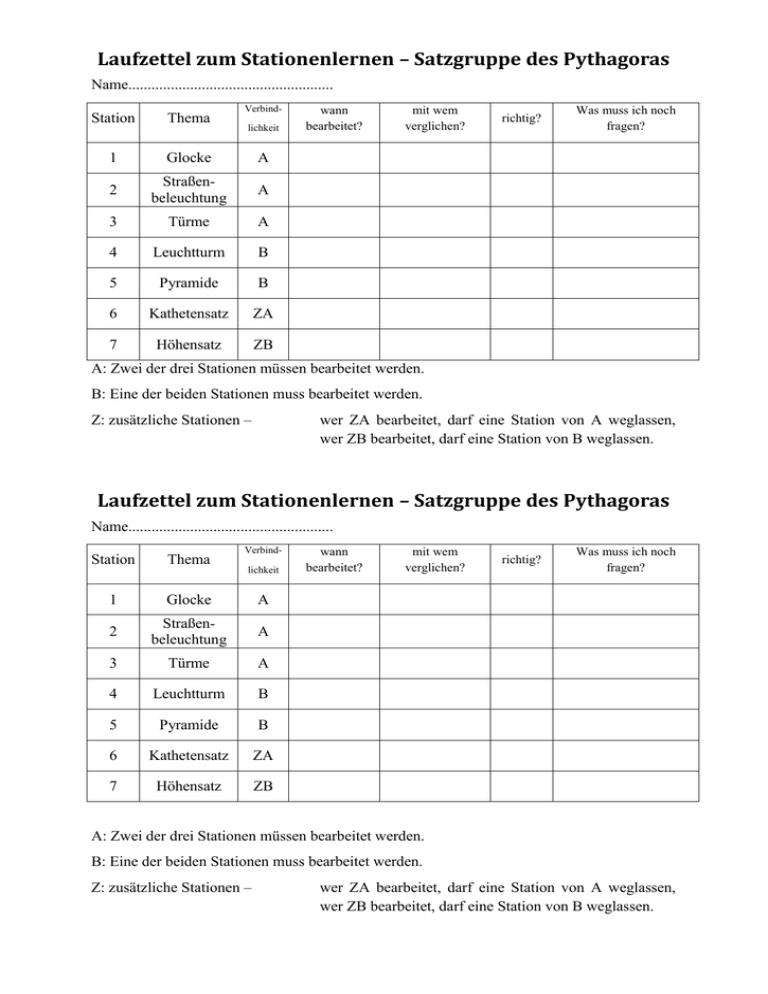
Laufzettel zum Stationenlernen – Satzgruppe des Pythagoras
Name.....................................................
Verbind-
Station
Thema
1
Glocke
A
2
Straßenbeleuchtung
A
3
Türme
A
4
Leuchtturm
B
5
Pyramide
B
6
Kathetensatz
ZA
7
Höhensatz
ZB
lichkeit
wann
bearbeitet?
mit wem
verglichen?
richtig?
Was muss ich noch
fragen?
A: Zwei der drei Stationen müssen bearbeitet werden.
B: Eine der beiden Stationen muss bearbeitet werden.
Z: zusätzliche Stationen –
wer ZA bearbeitet, darf eine Station von A weglassen,
wer ZB bearbeitet, darf eine Station von B weglassen.
Laufzettel zum Stationenlernen – Satzgruppe des Pythagoras
Name.....................................................
Verbind-
Station
Thema
1
Glocke
A
2
Straßenbeleuchtung
A
3
Türme
A
4
Leuchtturm
B
5
Pyramide
B
6
Kathetensatz
ZA
7
Höhensatz
ZB
lichkeit
wann
bearbeitet?
mit wem
verglichen?
richtig?
Was muss ich noch
fragen?
A: Zwei der drei Stationen müssen bearbeitet werden.
B: Eine der beiden Stationen muss bearbeitet werden.
Z: zusätzliche Stationen –
wer ZA bearbeitet, darf eine Station von A weglassen,
wer ZB bearbeitet, darf eine Station von B weglassen.
Stationenlernen – Satzgruppe des Pythagoras
Die Glocke des KPG – Station 1
Vor jeder Unterrichtsstunde machen sich Herr C. und Herr H. auf den Weg in die
Katakomben des KPG um die Schulglocke auf dem Dachboden des Hauptgebäudes zu läuten.
An der Glocke hängt ein langes Seil, welches bis in den Keller ragt.
Herr C. und Herr H. überlegen, wie man die Länge des Seils bestimmen könnte, ohne dieses
von der Schulglocke zu lösen.
Mit einem Metermaß bestückt macht sich Herr C. an die Arbeit und murmelt: „… wenn ich
das Ende des Seils um 2 m seitlich aus der vertikalen Position bewege, so hebt sich das
Seilende dabei um 10 cm.“
Bearbeite folgende Aufgaben
a) Fertige eine Skizze mit allen Angaben aus obigem Text an.
b) Berechne die Länge des Seils.
2m
Hinweiskarte 1 A - Die Glocke und das Seil
Document1
QUA-LiS.NRW
Stationenlernen – Satzgruppe des Pythagoras
Die Straßenbeleuchtung der Berliner Straße (Station 2)
Nicht nur auf der Berliner Straße findet man Straßenbeleuchtungen, die mit einem Seil mittig
über der Straße zwischen zwei Masten bzw. Häusern befestigt sind. Die Skizze einer solchen
„Laterne“ sieht wie folgt aus:
Durch das Gewicht der Lampe hängt das Befestigungsseil in der Mitte durch. Der Abstand der
Befestigungsmasten beträgt 12 m. Das Befestigungsseil ist 12,10 m lang.
Bearbeite folgende Aufgaben in deinem Heft.
a) Wie weit hängt die Lampe „durch“?
b) Im Sommer dehnt sich das Befestigungsseil aufgrund von Wärme um 3% aus.
Wie tief senkt sich die Lampe im Vergleich zu Aufgabenteil a)?
[Hinweis: Fertige zunächst eine Skizze an!]
Document1
QUA-LiS.NRW
Stationenlernen – Satzgruppe des Pythagoras
Zwei Türme – Station 3
Tief verborgen hinter der ehemaligen Ritterburg „Haus Graven“ befinden sich zwei Türme
auf einer ebenen Lichtung. Der eine Turm ist 60 Fuß 1 hoch, der andere 80 Fuß hoch. Ihr
Abstand beträgt 100 Fuß.
Für die beiden Vögel im unteren Bild ist der Weg von der Turmspitze bis zu einem Brunnen
zwischen den Türmen gleich lang.
Bearbeite die folgende Aufgabe in deinem Heft:
a) Fertige eine Skizze mit allen Angaben aus obigem Text an.
b) Berechne, wie weit der Brunnen jeweils von den Türmen2 entfernt ist (gemessen
jeweils vom Fuß des Turmes zur Mitte des Brunnens).
1
Ein „Fuß“ ist eine alte Längeneinheit, die sich aus der Länge eines Fußes abgeleitet hat.
2
Gemeint ist hier die Entfernung am Boden zwischen Turm und dem Brunnen.
Document1
QUA-LiS.NRW
Stationenlernen – Satzgruppe des Pythagoras
Der lange Leuchtturm von Langerland – Station 4
Auf der schönen Insel Langerland soll in naher Zukunft ein
Leuchtturm gebaut werden. Man streitet noch, wie hoch er
werden soll:

für die Lampe in Höhe von h = 30 m spricht: der Turm
wird nicht ganz so teuer.

für die Lampe in Höhe von h = 32 m spricht: das Licht
ist viel weiter sichtbar.
Hinweis: Der Erdradius beträgt 𝑟 ≈ 6370 𝑘𝑚.
Bearbeite folgende Aufgaben in deinem Heft:
Abbildung 1:Planung des
Langerlander Leuchtturms
a) Erstelle eine eigene geeignete Skizze zum Sachverhalt. (Bei Bedarf kannst du dir eine
Hinweiskarte dazu holen.)
b) Zeige, dass für die Sichtweite 𝑠 gilt: 𝑠 = √2𝑟ℎ + ℎ2 .
c) Berechne jeweils die Sichtweite für einen Leuchtturm mit h = 30 m bzw. h = 32 m.
d) Nimm begründet Stellung zu dem zweiten Argument, das in Langerland vorgebracht
wird.
e) Warum kann man für die Sichtweite als „Faustformel“ s  2rh benutzen?
Document1
QUA-LiS.NRW
Stationenlernen – Satzgruppe des Pythagoras
Hinweiskarte 4 A – Der lange Leuchtturm von Langerland
Hinweiskarte 4 B – Der lange Leuchtturm von Langerland
Hinweiskarte 4 C – Der lange Leuchtturm von Langerland
Document1
QUA-LiS.NRW
Stationenlernen – Satzgruppe des Pythagoras
Die Cheopspyramide – Station 5
Vor rund 4500 Jahren wurde die Cheopspyramide erbaut; sie ist die größte ägyptische
Pyramide (siehe Foto).
Abbildung 2: Cheops Pyramide. (Foto von Nina Aldin Thune, User:[email protected])
Die quadratische Grundfläche der Cheopspyramide hatte ursprünglich eine Seitenlänge von
233 m. Die Seitenkante der Pyramide war 221 m lang.
Bearbeite folgende Aufgaben in Deinem Heft:
a) Fertige zunächst eine geeignete Skizze an.
b) Berechne die ursprüngliche Höhe der Pyramide.
c) Heute hat die Cheopspyramide eine Seitenlänge von 227 m und eine Seitenkante von
218 m. Wie viel Meter ist die Pyramide durch Verwitterung niedriger geworden?
Document1
QUA-LiS.NRW
Stationenlernen – Satzgruppe des Pythagoras
Hinweiskarte 5 A - Die Cheopspyramide
a) Beschrifte zunächst alle bekannten Seitenlängen und markiere rechte Winkel.
b) Trage weitere wichtige Linien ein und markiere rechte Winkel an diesen Linien.
Hinweiskarte 5 B – Die Cheopspyramide
s
s
h
d
a
a
a) Berechne zunächst die Diagonalen im Quadrat aus den Seitenlängen a.
b) Berechne die Höhe h im senkrecht stehenden Dreieck.
Document1
QUA-LiS.NRW
Stationenlernen – Satzgruppe des Pythagoras
Der Kathetensatz – Station 6
Für jedes rechtwinklige Dreieck gilt:
Das Quadrat über einer Kathete ist flächengleich zum Rechteck aus der Hypotenuse und
dem anliegenden Hypotenusenabschnitt.
Wenn der rechte Winkel bei C ist, gilt:
𝑎2 = 𝑐 ⋅ 𝑝
𝑏2 = 𝑐 ⋅ 𝑞
a) Formuliere den Kathetensatz zu folgenden Dreiecken:
b) Berechne jeweils die Seite x:
c) Beweise den Kathetensatz.
Du kannst einen zeichnerischen (Puzzle-) Beweis durchführen, dazu gibt es die
Hinweiskarte 6 Z.
Du kannst einen algebraischen Beweis durchführen, dazu gibt es die Hinweiskarte
6 A.
Document1
QUA-LiS.NRW
Stationenlernen – Satzgruppe des Pythagoras
Hinweiskarte 6 A – Der Kathetensatz
Gehe wie folgt vor:
1.
Drücke ℎ𝑐 mithilfe des Satzes des Pythagoras jeweils im Dreieck 𝐷𝐵𝐶 und 𝐴𝐷𝐶 aus
und setze die beiden Ausdrücke einander gleich.
2.
Drücke nun 𝑏 im Dreieck 𝐴𝐵𝐶 mithilfe des Satzes des Pythagoras aus und setze es in
die Gleichung aus 1.) ein.
3.
Drücke schließlich 𝑞 durch 𝑐 und 𝑝 aus und setzte es in die Gleichung aus 2.) ein.
Löse diese dann auf und erhalte den Kathetensatz.
Formuliere deinen Beweis schriftlich.
Hinweiskarte 6 Z – Der Kathetensatz
Erkläre, nach welchem System das Puzzle
hergestellt wurde und inwiefern sich daraus der
Kathetensatz ergibt.
Erläutere,
dass
entsprechende
zueinander identisch sind.
Puzzleteile
Formuliere deinen Beweis in eigenen Worten.
Document1
QUA-LiS.NRW
Stationenlernen – Satzgruppe des Pythagoras
Der Höhensatz des Euklid - Station 7
a) Formuliere den Höhensatz zu folgenden Dreiecken:
b) Berechne die Höhen und die Flächeninhalte für die folgenden Dreiecke:
c) Beweise den Höhensatz.
Es gibt die Hinweiskarte 7 zu einem algebraischen Beweis.
Document1
QUA-LiS.NRW
Stationenlernen – Satzgruppe des Pythagoras
Hinweiskarte 7 – Der Höhensatz
Gehe wie folgt vor:
1.
Drücke ℎ𝑐 2 im Dreieck 𝐴𝐷𝐶 mit Hilfe des Satzes des Pythagoras aus.
2.
Drücke 𝑏 2 durch den Kathetensatz aus, setze es in 1.) ein und rechne aus.
Formuliere deinen Beweis schriftlich.
Document1
QUA-LiS.NRW