ARBEITSBLATT Nummer eingeben
Werbung
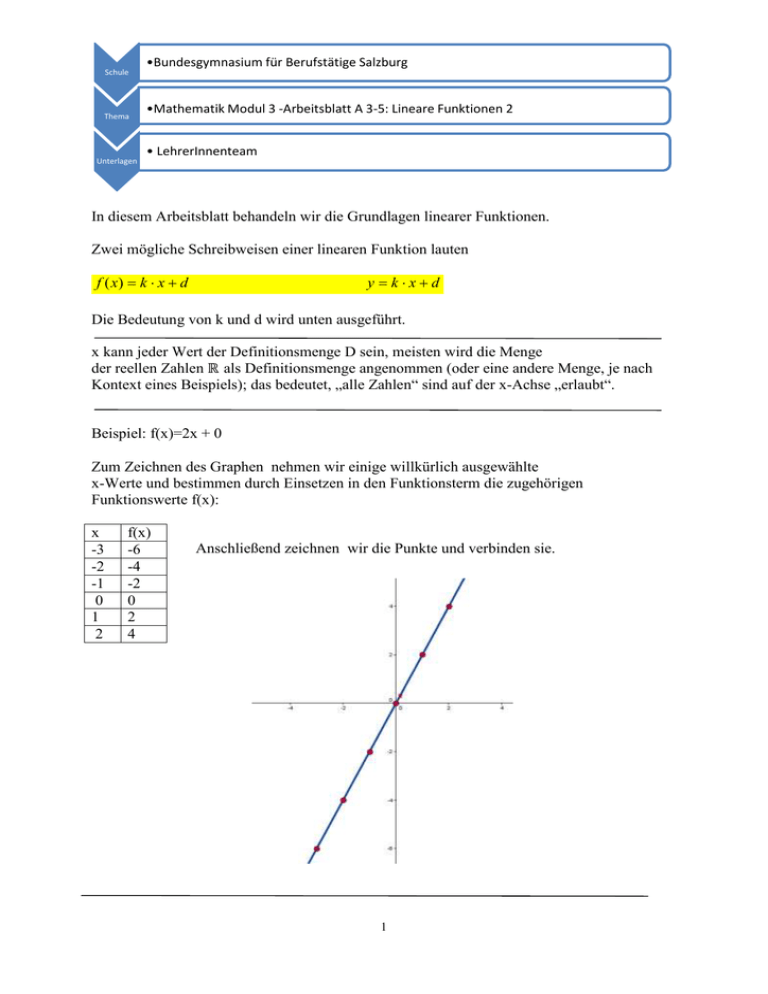
Schule Thema Unterlagen •Bundesgymnasium für Berufstätige Salzburg •Mathematik Modul 3 -Arbeitsblatt A 3-5: Lineare Funktionen 2 • LehrerInnenteam In diesem Arbeitsblatt behandeln wir die Grundlagen linearer Funktionen. Zwei mögliche Schreibweisen einer linearen Funktion lauten f ( x) k x d y kxd Die Bedeutung von k und d wird unten ausgeführt. x kann jeder Wert der Definitionsmenge D sein, meisten wird die Menge der reellen Zahlen ℝ als Definitionsmenge angenommen (oder eine andere Menge, je nach Kontext eines Beispiels); das bedeutet, „alle Zahlen“ sind auf der x-Achse „erlaubt“. Beispiel: f(x)=2x + 0 Zum Zeichnen des Graphen nehmen wir einige willkürlich ausgewählte x-Werte und bestimmen durch Einsetzen in den Funktionsterm die zugehörigen Funktionswerte f(x): x -3 -2 -1 0 1 2 f(x) -6 -4 -2 0 2 4 Anschließend zeichnen wir die Punkte und verbinden sie. 1 Schule Thema Unterlagen •Bundesgymnasium für Berufstätige Salzburg •Mathematik Modul 3 -Arbeitsblatt A 3-5: Lineare Funktionen 2 • LehrerInnenteam Beispiel: f(x)=2x + 3 Der Graph von f(x) schneidet die y-Achse an der Stelle 3. Das erhält man sehr schnell, wenn im Funktionsterm für x den Wert Null einsetzt. Erkenntnis: d ist der Wert auf der y-Achse, bei dem der Graph der linearen Funktion f ( x) k x d die y-Achse schneidet. Bedeutung von k k bedeutet die Steigung der linearen Funktion. Die Steigung kann auf mehrere Arten verstanden werden. Zur Bestimmung von k können Sie ein beliebig großes Dreieck in dieser Form zeichnen: 2 Schule Thema Unterlagen •Bundesgymnasium für Berufstätige Salzburg •Mathematik Modul 3 -Arbeitsblatt A 3-5: Lineare Funktionen 2 • LehrerInnenteam Die Steigung k ist das Verhältnis von Δy zu Δx. y Also k x Beim obigen Beispiel f(x)=2x + 3 ist eines dieser möglichen „Steigungsdreicke“ in der Graphik gezeichnet. Die Steigung ist hier also 2 Sie können aber auch jedes ähnliche Dreieck zur Bestimmung von k verwenden. 3 Schule Thema Unterlagen •Bundesgymnasium für Berufstätige Salzburg •Mathematik Modul 3 -Arbeitsblatt A 3-5: Lineare Funktionen 2 • LehrerInnenteam Die Bedeutung von k kann auch so verstanden werden: „geht man um 1 nach rechts“ (bessser: erhöht man x um 1) so geht man die Steigung k rauf (oder runter, wenn k negativ ist). Man erhält so den wichtigen Zusammhang bei linearen Funktionen (sozusagen ein charakteristisches Merkmal): f(x+1)=f(x)+k Geht man um 2 nach rechts, so geht man 2 mal die Steigung nach oben (oder unten): f(x+2)=f(x)+2k und allgemein: f(x+Δx)=f(x)+k Δx oder umgeformt: k f ( x x) f ( x) y oder eben k x x 4 Schule Thema Unterlagen •Bundesgymnasium für Berufstätige Salzburg •Mathematik Modul 3 -Arbeitsblatt A 3-5: Lineare Funktionen 2 • LehrerInnenteam Anwendung: Bestimmung von k und d, wenn 2 Punkte gegeben sind (lineare Funktion vorausgesetzt). k y 3 1 x = 6 2 Man “setzt“ nun einen beliebigen Punkt der Geraden in die Funktionsgleichung ein: Ich wähle hier den Punkt P. 1 y xd 2 1 2 1 d 2 daraus folgt d=1,5 Lösung: 1 y x 1,5 2 Anwendung von f(x+Δx)=f(x)+k Δx f(x)=2x + 3 , 1 7 P Q 5 , ? Δx=6, also f(1 + 6) = 5 + 2 6 = 17 also 7 Q 17 natürlich könnte man auch einfach f(7) bestimmen, was wiederum 17 ergibt. 5 Schule Thema Unterlagen •Bundesgymnasium für Berufstätige Salzburg •Mathematik Modul 3 -Arbeitsblatt A 3-5: Lineare Funktionen 2 • LehrerInnenteam Hätten Sie in der Angabe nur die Steigung 2 gegegen, aber nicht den ganzen Funktionsterm, so ist die obige Formel sehr hilfreich. Eine weitere, sehr praktische Schreibweise von linearen Funktionen ist die sogenannte Achsenabschnittsform x y 1 a b a und b sind die eingezeichneten „Achsenabschnitte“ Die Steigung einer in der Achsenabschnittsform gegebenen Geraden lautet b b b oder oder a a a Übung: Begründen Sie das mit Hilfe der Graphik: 6 Schule Thema Unterlagen •Bundesgymnasium für Berufstätige Salzburg •Mathematik Modul 3 -Arbeitsblatt A 3-5: Lineare Funktionen 2 • LehrerInnenteam Beispiel: x y 1 4 5 Beispiel: x y 1 4 5 Umformen zu x y 1 4 5 7 Schule Thema Unterlagen •Bundesgymnasium für Berufstätige Salzburg •Mathematik Modul 3 -Arbeitsblatt A 3-5: Lineare Funktionen 2 • LehrerInnenteam Beispiel: x y 2 4 5 Umformen, bis rechts gleich 1 x y 1 8 10 Beispiel: 5 x 4 y 20 |: 20 x y 1 4 5 Nullstellen einer linearen Funktion Nullstellen bedeuten y=0, also Schnittpunkte des Graphen mit der x-Achse. Wiederum ist hier die Achsenabschnittsform sehr praktisch: x y 1 4 5 Daraus folgt Nullstelle bei 4 (=a). Ist die Funktion gegeben als f ( x) k x d oder y kxd so „setzt man die Funktion Null“, schreibt also statt f(x) den Wert 0. Beispiel: f(x)=2x+4 0=2x+4, woraus x=-2 folgt. Die Nullstelle liegt also beim Punkt 2 N 0 . Wann hat eine lineare Funktion keine Nullstelle? Wenn k=0 und d ungleich 0. 8 Schule Thema Unterlagen •Bundesgymnasium für Berufstätige Salzburg •Mathematik Modul 3 -Arbeitsblatt A 3-5: Lineare Funktionen 2 • LehrerInnenteam Verwendete GeoGebra-Arbeitsblätter: auf: abendgymnasium.schule.at Mathematik/Dominik/math&comp/lineare Funktion 9











