Windkanal_Praktikumsbericht

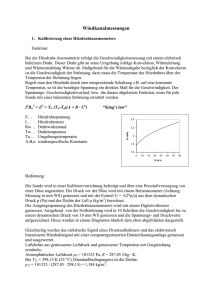
Aerodynamische Untersuchung eines Flügelmodells im grossen Windkanal
Einleitung
Windkanäle gehören in der Strömungstechnik zu einem der mächtigsten Werkzeuge. Trotz fortschreitender Computerleistung und Programmen wie CFD (numerischer Teil), darf man den Windkanal als praktischen Teil nicht unterschätzen. Erst beide Teile zusammen ergeben sinnvolle und sichere
Ergebnisse in der Fluiddynamik.
In diesem Praktikum erhalten wir einen Einblick in den Windkanal anhand der aerodynamischen
Untersuchung eines Flügelmodells. Wir lernen einige Messmethoden kennen und bestimmen die
aerodynamischen Eigenschaften des Modells.
Versuchsaufbau
Die Untersuchung am Flügelmodell wurde in einem geschlossenen Unterschallwindkanal durchgeführt. Das Flügelmodell wurde auf einer drehbaren Scheibe festgemacht, welche mit einem Elektromotor gesteuert werden konnte. Dadurch konnten beliebige Anstellwinkel zur Strömungsrichtung
von ausserhalb und während des Betriebs eingestellt werden.
Vor der ganzen Versuchsreihe mussten die Geräte kurz kalibriert werden. Im Windkanal befindet sich
ein Pitot Rohr, welches den Druck am engsten Querschnitt misst. Zusammen mit den Werten aus den
Sensoren, welche den Druck am grössten Querschnitt vor der Düse messen (jedoch in Form einer
Spannung) und einem Manometer konnte das Verhältnis des dynamischen Drucks zur gemessenen
Spannung der Sensoren bei zwei Betriebspunkten des Windkanals (30% und 59.5%) gemessen und
der Umrechnungsfaktor berechnet werden. Der Umrechnungsfaktor betrug bei diesem Versuch
284.87 Pa/V.
[Pa/V]
900
800
700
600
500
400
300
200
100
0
800.25
[Pa/V]
198.6
0.706
2.818
Abbildung 1
Bericht Windkanal
Petros Papadopoulos
06-916-117
1
Versuche
Es wurden drei kurze Messmethoden am Flügelmodell gezeigt und ein Versuch durchgeführt, um das
aerodynamische Verhalten des Modells „NACA0012“ zu untersuchen.
Bei der ersten Messmethode wurde der kritische Anstellwinkel, bei dem die Strömung um das
Flügelmodell komplett abriss, bestimmt. Entgegen der Erwartung wanderte der Abrisspunkt nicht
gleichmässig nach hinten; die Strömung riss ab einem Winkel von 12° plötzlich komplett ab. Bei 12°
war die untere Hälfte in der Abrisszone drin, die obere jedoch nicht.
Die zweite Messung beschäftigte sich mit der Turbulenz. Turbulenz kann man in einem
geschlossenen Windkanal nicht sehen, aber hören. Mit einem Stetoskop und einem sehr dünnen
Rohr konnten die Schwingungen in der Strömung herausgehört werden (ein leises Rauschen).
Zum Schluss kam noch das Sichtbarmachen der Wirbel am Rande des Flügelmodells mittels einer
kleinen Rauchsonde. Es zeigte sich, dass sich die Wirbel aufgrund des Druckausgleichs über den Rand
noch sehr lange der Strömung entlang ausbreiteten.
Beim Versuch wurde das Flügelmodell bei den beiden oben beschriebenen Betriebspunkten der
Strömung für Winkel von -20° bis 20° ausgesetzt. Die gesammelten Daten wurden in einer Excel Tabelle gespeichert, die dann mittels eines vorgefertigten MATLAB Programms grafisch dargestellt
werden konnten. In einem letzten Durchlauf wurde eine Platte an das Modell angeschraubt, welche
ein Winglet simulieren sollte. Die Messung entstand bei 59.5% Leistung des Windkanals.
Resultate und Analyse
Die drei Messreihen zeigten, dass die Wirbel am Rande des Flügels einen erheblichen Einfluss auf die
Strömung haben. Bei 12° Anstellwinkel induzierten die entstehenden Wirbel eine leichte Änderung
der Strömungsrichtung in der oberen Hälfte des Flügels; die Strömung hatte jetzt einen kleineren
Anstellwinkel und riss deshalb nicht ab, während sich der untere Bereich komplett im Abriss befand.
Abbildung 2
In Abb. 2 wurde die Auftriebskraft zum Anstellwinkel grafisch dargestellt. Die erste Messung entspricht dabei 30% Leistung des Windkanals, die zweite und dritte 59.5%. Die dritte Messung fand mit
angeschraubtem „Winglet“ statt.
Bericht Windkanal
Petros Papadopoulos
06-916-117
2
Abbildung 3
Abb. 3 zeigt die Korrelation zwischen Auftriebskraft und Widerstandskraft. Deutlich erkennbar ist der
Nullwiderstand, der bei cA = 0 abgelesen werden kann. Bei allen drei Messungen ist dieser, obwohl er
eine Funktion der Reynoldszahl ist, identisch.
Diskussion
Aus der grafischen Darstellung der Abb. 2 sind einige interessante Punkte erkennbar. Das Flügelmodell hat keine Wölbung, was auch in den Resultaten sichtbar ist. Die Auftriebskraft ist für 0° ebenfalls
0. Weiterhin sieht man, dass die Auftriebskraft nicht sehr stark von der Anströmgeschwindigkeit und
damit von der Reynoldszahl abhängig. Beim „Winglet“ sieht man, dass mehr Anstellwinkel möglich ist
und die Auftriebskraft leicht höher ausfällt als ohne „Winglet“. Die maximale Auftriebskraft ist ausschlaggebend für die Pistenlänge; je höher die Auftriebskraft, desto kürzer kann die Pistenlänge ausfallen. Ebenso ist der kritische Winkel von 12°, bei dem die Strömung abreisst sehr gut sichtbar.
In der Abb. 3 erkennt man nebst dem Nullwiderstand, dass das Profil mit „Winglet“ erst ab einem cW
– Wert von etwa 0.05 einen stärkeren Auftriebswert aufweist. Die Abhängigkeit des Abrisspunktes
von der Reynoldszahl sieht man bei den oberen cA – Werten; bei höherer Reynoldszahl dauert es
länger, bis die Strömung komplett abreisst. Der induzierte Widerstand jedoch ist nur ausschliesslich
vom Anstellwinkel abhängig, was man an den Steigungen der Messungen für cW < 0.05 gut sehen
kann.
Schlussworte
Abschliessend möchte ich noch zu diesem Praktikum als erstes Marc Immer danken, der sich sehr viel
Mühe beim Erklären von unseren Fragen gegeben hat. Das Praktikum war eine sehr interessante
Erfahrung und auch zeitlich mit der Fluiddynamik II Vorlesung gut überschneidend, so dass man auch
die Theorie verstehen konnte.
Bericht Windkanal
Petros Papadopoulos
06-916-117
3