Protokoll
Werbung

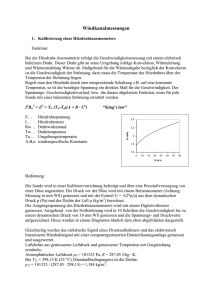
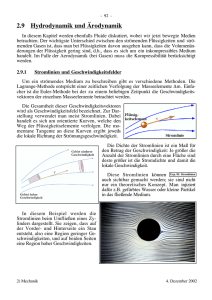
Westfälische Wilhelms – Universität zu Münster Physikalisches Institut Experimentelle Übungen für Fortgeschrittene Sommersemester 2004 Aufgabe 123 Laminare und turbulente Strömungen in glatten Rohren Durchgeführt am: 18. Mai 2004 Durchgeführt und ausgewertet von: Martin Stadlbauer [email protected] Martin Höhn 2 I Einleitung Durchläuft eine Flüssigkeit ein glattes Rohr, so können zwei Arten von Strtömung auftreten, die laminare und die turbulente. Im laminaren Fall kommt das Hagen-Poiseuille-Gesetz zur Geltung. Eine wichtige Kenngröße der Strömung ist die Reynoldszahl. Hat sie einen bestimten Wert erreicht, schlägt die laminare Strömung allmählich in eine turbulente um. Weiter wichtige Größen sind die Widerstandszahl λ und a, b, welche wesentlich von der Rohrgeometrie abhängen. II Theorie Werden zwei parallele Platten gegeneinander bewegt, zwischen denen sich eine Flüssigkeit oder ein Gas befindet, so muss die Reibungskraft FR überwunden werden. Ist die Flüssigkeitsströmung schleichend, d. h. laminar, gilt: - die Flüssigkeit haftet an den Begrenzungen - die Flüssigkeitsschichten gleiten übereinander hinweg, es kommt zu keiner Durchmischung Für die Kräfte gilt dann: -FR = F = η·A·dv/dx Dies ist die Definition der Viskosität einer Flüssigkeit, Einheit: 1Pa·s. Werden nun nicht zwei parallele Platten betrachtet, sondern ein Rohr so sind die Überlegungen analog zu übertragen. Auch hier haftet die Flüssigkeit n den Wänden und es kommt zu keiner Durchmischung. Zur Aufrechterhaltung der Strömung ist ein äußerer Druck erforderlich, der läng der Rohrrichtung um Δp abfällt. Aus der Definition des Druckes ergibt sich direkt bei einem Rohr mit kreisförmigen Durchschnitt: F = π r² Δp Durch Gleichsetzen der beiden Kraftgleichungen ergibt sich durch Integrieren: v(r ) p ( R ² r ²) 4l Also liegt ein parabolisches Geschwindigkeitsprofil vor. Der Volumenstrom ist definiert durch I = V/t 3 Für ein Volumenelement gilt dV = dA · v · t Weiter gilt mit dA= 2π·r·dr durch Einsetzen und Integrieren das Hagen-Poiseuille’sche Gesetz: Iv p R 4 8l Turbulenten Strömungen sind dadurch gekennzeichnet, dass es zu Wirbelbildung kommt, an den Begrenzungen die Geschwindigkeit von Null verschieden ist und das Geschwindigkeitsprofil nicht mehr parabolisch, sondern flach ist. Die Komplexität dieses Problems erfordert einen integralen Ansatz, es wird die dimensionslose Widerstandszahl λ eingeführt. F = λ·A· ½ ·ρ·v² Während bei laminarer Strömung Reibungsarbeit pro Volumen verrichtet wird, wird bei der turbulenten Strömung Beschleunigungsarbeit pro Volumen verrichtet. Im turbulenten Fall ergibt sich: ² R 5 p Iv l Nach dem Reynoldschen Ähnlichkeitsgesetz sind zwei Strömungen ähnlich (d. h. sie besitzen dasselbe auf die mittlere Geschwindigkeit normierte Geschwindigkeitsprofil), wenn ihre Reynoldszahl Re dieselbe ist, wobei gilt: Re R v R Iv Wenn die Reynoldszahl einen kritischen Wert erreicht, so kommt es zum Übergang von laminarer zu turbulenter Strömung. Für Rohrströmungen mit kreisförmigen Querschnitt ist Re = 1160, was allerdings keine scharfe Grenze darstellt. Die Widerstandszahl λ errechnet sich nach bereits oben genannter Formel zu ² R 5 p l I v2 Der Zusammenhang zwischen λ und Re lautet bei laminaren Strömungen 8 ln ln 8 ln Re Re 4 Bei doppellogarithmischer Auftragung erhält man also eine Gerade mit der Steigung –1. Allgemein gilt: a ln ln a b ln Re Re b Hierbei sind a und b allein vom Strömungstyp abhängige Konstanten. III Experiment Versuchsaufbau Es steht eine Messapparatur zur Verfügung, dessen Kernstück ein Rohr der Länge l bildet, durch das Wasser fließt. Der Druckabfall im Rohr ist durch ein Barometer ermittelbar. Je nach Druck steht ein Wassersäulenbarometer bzw. ein Barometer, bei dem eine Quecksilbersäule in Wasser schwimmt zur Verfügung. Zur Bestimmung der Viskosität des Wassers sind zwei Thermometer angebracht. Der Volumenstrom wird am Wasserhahn eingestellt und mit Hilfe von Messbechern und einer Stopuhr ermittelt. Messung Die Temperatur schwankte kaum, auf jeden Fall ist der Tabelle für die Viskosität von Wasser ein Wert von 0,93·10-3 Pa·s zu entnehmen. Bei der Messung der Drücke wurde ein Fehler von 0,2 cm eingeräumt. Bereits bei einem Barometerhöhenunterschied von 4 cm (was für fast alle Werte galt) liegt der Fehler unter 5 %. Die Fehler für die Volumina variierten und sind in der Tabelle aufgenommen, der Fehler für das Messen der Zeit lag bei 1s. Die Fehlerrechnung für den Volumenstrom wurde in der Tabelle durchgeführt und ist im Diagramm eingetragen (unter u_etaI[%/abs]). Für die Länge des Rohres gab die Messung: l = 0,560 m ± 0,002 m Fehler von 0,4 % gegenüber den anderen Fehlern vernachlässigbar. Ermittlung des Rohrradius Im Diagramm wurde η·Iv gegen Δp aufgetragen. Die ersten Werte liegen auf einer Geraden mit der Steigung: m = η·Iv / Δπ = (11,1 ± 3,1)·10-6 ml Für den Rohradium R gilt dann wegen R4 8l I v p 5 R_max = 2,06 mm R_min = 1,84 mm => R = 1,95 mm ± 0,11 mm Weiter sind mit Hilfe der oben genannten Formeln die Reynoldszahl Re und die Widerstandszahl λ berechnet worden. Sie sind für jeden Messwert in der Tabelle aufgeführt. Durch das Auftragen von ln λ gegen ln Re ergeben sich die Konstanten a und b folgendermaßen: Laminarer Fall: Die Gerade gehorcht der Gleichung y = 2,10 – 1,03 x Wie vorrausgesagt ist die Steigung also quasi –1. Für a = 8 ist ln a = 2,08, was der ermittelten 2,10 sehr nahe kommt. Turbulenter Fall: Die Gerade gehorcht der Gleichung y = -3,20-0,22 x Für die Steigung lässt sich dank Fehlerbalken auch ein (großzügiger!) Fehler entnehmen: b= -m = 0,22 ± 0,19 Dann ist a = e-3,20 = 0,041. Aus dem Diagramm ist zu entnehmen, dass die kritische Reynoldszahl zwischen 1082 und 1352 liegen muss. Diskussion Der Fehler beim Rohrradius liegt unter 6%, der gefundene Wert ist durchaus plausibel. Der gefundene Bereich für die Reynoldszahl entspricht den Erwartungen von 1160. Die gefundenen a und b im laminaren Fall entsprechen fast exakt der erwarteten 8 bzw. –1. Das gefundene b im turbulenten Fall kommt der erwarteten -0,25 sehr nahe, da a weicht stark von 0,067 ab, liegt aber in der richtigen Größenordnung.