Kapitel9

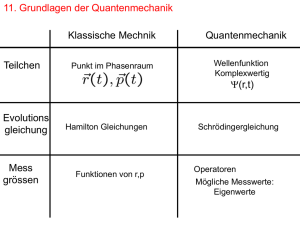
8 Das Bohrsche Atommodell
1. Einführung
1.1. Quantenmechanik – versus klassische Theorien
1.2. Historischer Rückblick
2. Kann man Atome sehen? Größe des Atoms
3. Weitere Eigenschaften von Atomen: Masse, Isotopie
4. Atomkern und Hülle: das Rutherfordexperiment
5. Das Photon: Welle und Teilchen
6. Teilchen als Welle (de Broglie)
7. Heisenbergsche Unschärferelation
8. Das Bohrsche Atommodell
8.1. Experimenteller Befund 1: Diskrete Spektren
8.2. Experimenteller Befund 2: Franck Hertz Versuch
8.3. Model: Die Bohrschen Postulate
8.4. Veranschaulichung des Models 1: Rydbergatome
8.5. Korrektur durch endliche Kernmasse
8.6. Veranschaulichung des Models 2: Myonische Atome
8.7. Veranschaulichung des Models 3: Positronium, Antiwasserstoff
8.8. Weitere Korrektur: Sommerfeld
8.9. Bohrmodell und DeBroglie Wellen
8.10. Die Grenzen des Bohrmodells
9. Grundlagen der Quantenmechanik
9. Grundlagen der Quantenmechanik
9.1. Operatoren, Messwerte
9.2. Zeitabhängige und stationäre Schrödingergleichung
9.3. Beispiel 1: Ebene Wellen als Lösung der
Potentialfreien Schrödingergleichung
9.4. Beispiel 2: Der unendliche Potentialtopf
9.5. Beispiel 3: Die Potentialstufe
9.6. Der Tunneleffekt
9.6.1. Tunneleffekt Beispiel 1: Alphazerfall von Kernen
9.6.2. Tunneleffekt Beispiel 2: Rastertunnelmikroskop
9.7 Der (quantenmechanische) harmonische Oszillator
9. Grundlagen der Quantenmechanik
Klassische Mechanik
Quantenmechanik
Teilchen
Punkt im Phasenraum
Wellenfunktion
komplexwertig
Y(r,t)
normierbar s Y2(x) dx =1
stetig differenzierbar
Evolutions
gleichung
Hamilton Gleichungen
Schrödingergleichung
Mess
grössen
Jeder physikalischen Größe A(r, p)
(“Observable“), die eine Funktion
von Ort r und Impuls p eines
Teilchens ist, entspricht ein
Differentialoperator
Â, den man erhält, indem
man p durch -iħ  ersetzt:
Wellengleichung für ein Teilchen
im Potentzial V(r)
Zeitabhängige SG daraus folgt
mit Y(r),t)=(r) eiE/~ t die stationäre SG,
siehe extra slide
Funktionen von r,p
Ort:
x(t)
Operatoren
X (Multiplikation mit x)
Prinzip 1:
Basis
Prinzip 2:
Messung:
Jede Einzelmessung kann
als Zahlenwert nur die
Eigenwerte des Operators
liefern.
Beispiel 1: Impuls
Eigewertgleichung:
Impuls mv(t)=m dx(t)/dt
Drehimpuls L=
Energie
(Hamilton-Funktion)
E  H (r , p) 
p
Hamiltonoperator
2
2
2m
Drehimpulsoperator
 V (r )
ˆ  H ( r , i  )      V ( r )
H
2m
Abgeleitet,
allgemein:
ersetzt x,p
durch
Operatoren
Beispiel 2: Energie:
H (x) = E (x)
Energieoperator Energieeigenwerte
(Diskrete Energien)
9. Grundlagen der Quantenmechanik
Komplexwertige Wellenfunktion Y(x,t)
Zeitabhängige Schrödingergleichung:
Beispiel: deBroglie Ebene Welle
A(x,t) = A0 cos(kx - t)
Für zeitunabhängiges Potential
Ansatz:
Wie kommt man drauf?
Geraten, aber naheliegend!
Wieso ist das die Energie?
Zunächst nur Konstante die E heisst
Dimension Energie: ~ == Energie*Zeit
Gesamtenergie klärt
sich bei Anwendung
9. Grundlagen der Quantenmechanik
Komplexwertige Wellenfunktion Y(x,t)
Zeitabhängige Schrödingergleichung:
Beispiel: deBroglie Ebene Welle
A(x,t) = A0 cos(kx - t)
Für zeitunabhängiges Potential
Ansatz:
Stationäre Schrödingergleichung
Linear:
wenn a(x) und b(x) Lösungen sind
Löst auch
Y(x) = A * a(x) + B * b(x)
Bsp: Überlagerungen von Ebenen Wellen zu Wellenpaketen
9. Grundlagen der Quantenmechanik
Komplexwertige Wellenfunktion Y(x,t)
Zeitabhängige Schrödingergleichung:
Beispiel: deBroglie Ebene Welle
A(x,t) = A0 cos(kx - t)
Für zeitunabhängiges Potential
Ansatz:
Stationäre Schrödingergleichung
Beispiel 1: V(x)=0
Allgemeiner Ansatz: Y(x)=Aeikx + B e-ikx
löst:
Konstante E
Ist die
Energie des Systems
(da V(x)=0 nur kinetische Energie)
Kinetische Energie
9. Grundlagen der Quantenmechanik
Komplexwertige Wellenfunktion Y(x,t)
Zeitabhängige Schrödingergleichung:
Beispiel: deBroglie Ebene Welle
A(x,t) = A0 cos(kx - t)
Für zeitunabhängiges Potential
Ansatz:
Stationäre Schrödingergleichung
Allgemeiner Ansatz: Y(x)=Aeikx + B e-ikx
Beispiel 1: V(x)=0
löst:
Mit Zeitabhängigkeit:
9. Grundlagen der Quantenmechanik
Stationäre Schrödingergleichung
Beispiel 2: Unendlicher Potentialkasten
V(x)=
0 für 0·x¸L
1 sonst
Y(x)=Aeikx + B e-ikx
Y(x·0)=Y(x¸L)=0
Randbedingung 1
Y(x=0) = 0 ) A+B=0
) Y(x)=A(eikx - e-ikx)=2iA sin(kx)
Randbedingung 2
Y(x=L) = 2iA sin(kL) = 0
) kL= np (n=1,2,3 ...)
Quantenzahlen n
N ist nicht Anzahl der Knoten
N=0 ist psi=o kein Teilchen
Mögliche Energieniveaus in der Box:
Stationäre Wellenfunktionen in der Box:
fehlte
9. Grundlagen der Quantenmechanik
Stationäre Schrödingergleichung
Bemerkungen:
1) Nur feste Impulse
2) Nullpunktsenergie (steigt wenn L->0)
3) Woher kommt die Quantisierung??
4) Zeitentwicklung der Zustände?
hängt von En (n2) ab!
Mögliche Energieniveaus in der Box:
Stationäre Wellenfunktionen in der Box:
9. Grundlagen der Quantenmechanik
Stationäre Schrödingergleichung
Bemerkungen:
1) Nur feste Impulse
2) Nullpunktsenergie (steigt wenn L->0)
3) Woher kommt die Quantisierung??
4) Zeitentwicklung der Zustände?
hängt von En (n2) ab!
Mögliche Energieniveaus in der Box:
Stationäre Wellenfunktionen in der Box:
9. Grundlagen der Quantenmechanik
Visualisierung der Zeitabhängikeit der Zustände:
a) Eigenzustände haben keine Zeitabhängikkeit der Aufenthaltswahrscheinlichkeit
Real Imaginärteil
Aufenthaltswahrscheinlichkeit
http://www.quantum-physics.polytechnique.fr/en/stationary.html
9. Grundlagen der Quantenmechanik
Stationäre Schrödingergleichung
Bemerkungen:
1) Nur feste Impulse
2) Nullpunktsenergie (steigt wenn L->0)
3) Woher kommt die Quantisierung??
4) Zeitentwicklung der Zustände?
5) Was passiert wenn man
andere Energie, Wellenfunktion
erzwingt?
z.B. Barriere aufziehen?
Mögliche Energieniveaus in der Box:
Stationäre Wellenfunktionen in der Box:
9. Grundlagen der Quantenmechanik
Imagine a quantum particle initially described by a Gaussian wave
packet centered at the middle of a square box, with momentum
zero.
WAS PASSIERT??
http://rugth30.phys.rug.nl/quantummechanics/potential.htm
9. Grundlagen der Quantenmechanik
Teilchen mit Anfangsimpuls in 2 dim Potentialtopf
(kx , ky) = (0.86 , 0.5)
(sx , sy) = (2l , 2l)
http://rugth30.phys.rug.nl/quantummechanics/potential.htm
9. Grundlagen der Quantenmechanik
Wichtigste Lehre aus dem Beispiel
unendlicher Potentialtopf:
Quantenzahlen, und die Quantisierung
einer Größe sind Folge der Randbedingungen
und der Forderung nach
Stetigkeit und Differenzierbarkeit
Am Beispiel der Potentialtopf ist dies ohne
explizites Lösen der Schrödingergleichung
ersichtlich, bei „echten“ Potentialen ist dies
etwas versteckter, das Prinzip ist aber gleich.
Ausblick: Die Quantisierung des Drehimpulses wird sich
auch herausstellen als Folge von Randbedingungen,
allerdings nicht des Potentials, sondern aus der Rotation
Mögliche Energieniveaus in der Box:
Stationäre Wellenfunktionen in der Box:
9. Grundlagen der Quantenmechanik
9.1. Operatoren, Messwerte
9.2. Zeitabhängige und stationäre Schrödingergleichung
9.3. Beispiel 1: Ebene Wellen als Lösung der
Potentialfreien Schrödingergleichung
9.4. Beispiel 2: Der unendliche Potentialtopf
9.5. Beispiel 3: Die Potentialstufe
9.6. Der Tunneleffekt
9.6.1. Tunneleffekt Beispiel 1: Alphazerfall von Kernen
9.6.2. Tunneleffekt Beispiel 2: Rastertunnelmikroskop
9.7 Der (quantenmechanische) harmonische Oszillator
11.4. Potentialstufe
Bereich (I): V(x)=0 )
(I)
E(x)
Stationäre Schrödingergleichung
(II)
YI(x)=A eikx + B e-ikx
E0
Bereich (II):
a2
YII(x)=C eax + D e-ax
x
Y(x) soll stetig differentierbar auch bei x=0 sein (Randbedingung) )
YI(x=0)=YII(x=0)
)
A+B=C+D
(i)
) ik(A-B)=a(C-D) (ii)
11.4. Potentialstufe
Bereich (I): V(x)=0 )
(I)
E(x)
9. Grundlagen der Quantenmechanik Stationäre Schrödingergleichung
(II)
YI(x)=A eikx + B e-ikx
E0
Bereich (II):
a2
YII(x)=C eax + D e-ax
x
Y(x) soll stetig differentierbar auch bei x=0 sein (Randbedingung) )
YI(x=0)=YII(x=0)
)
A+B=C+D
(i)
) ik(A-B)=a(C-D) (ii)
Fall a) E<E0
a reel ) C=0 weil sonst YII(x!1) divergiert
C=0 Æ (i) Æ (ii) ) ik(A-B)=a (A+B) )
Verhältnis von Ein- und Auslaufenden Teilchen:
ik-a
ik+a
11.4. Potentialstufe
Bereich (I): V(x)=0 )
(I)
E(x)
Stationäre Schrödingergleichung
(II)
YI(x)=A eikx + B e-ikx
E0
Bereich (II):
a2
YII(x)=C eax + D e-ax
x
1.
Y(x)Potentialwall
soll stetig differentierbar
reflektiert vollständig
auch bei x=0 sein (Randbedingung) )
2. Wellenfunktion dringt in den klassisch verbotenen Bereich ein
YI(x=0)=YII(x=0)
) A+B=C+D
(i)
Energieerhaltung???

Et>~
) ik(A-B)=a(C-D)
(ii)
Fall a) E<E0
a reel ) C=0 weil sonst YII(x!1) divergiert
C=0 Æ (i) Æ (ii) ) ik(A-B)=a (A+B) )
Verhältnis von Ein- und Auslaufenden Teilchen:
ik-a
ik+a
11.4. Potentialstufe
Bereich (I): V(x)=0 )
(I)
E(x)
Stationäre Schrödingergleichung
(II)
YI(x)=A eikx + B e-ikx
E0
Bereich (II):
a2
YII(x)=C eax + D e-ax
x
Y(x) soll stetig differentierbar auch bei x=0 sein (Randbedingung) )
YI(x=0)=YII(x=0)
)
A+B=C+D
(i)
) ik(A-B)=a(C-D) (ii)
Fall b) E>E0
klassisch: Teilchen fliegt mit verminderter Geschwindigkeit weiter
11.4. Potentialstufe
Bereich (I): V(x)=0 )
(I)
E(x)
Stationäre Schrödingergleichung
(II)
YI(x)=A eikx + B e-ikx
E0
Bereich (II):
a2
YII(x)=C eax + D e-ax
x
Y(x) soll stetig differentierbar auch bei x=0 sein (Randbedingung) )
YI(x=0)=YII(x=0)
)
A+B=C+D
(i)
) ik(A-B)=a(C-D) (ii)
Fall b) E>E0
YII(x)=C eik‘x + D e-ik‘x
D=0, da keine Teilchen in (II) nach links fliegen
D=0 Æ (i) Æ (ii) ) ik(A-B)=-k‘ (A+B) )
11.4. Potentialstufe
Bereich (I): V(x)=0 )
E(x)
Stationäre Schrödingergleichung
(I)
YI(x)=A eikx + B e-ikx
|A|2
Bereich (II):
a2
E0
(II)
|D|2
|B|2
YII(x)=C eax + D e-ax
x
1. Auch wenn E>E0 wird ein Teil der Welle reflektiert! (Je mehr, je höher E_0)
2. Wellenfunktion
YI(x=0)=YII(x=0)
) A+B=C+D
(i)
) ik(A-B)=-a(C-D) (ii)
Fall b) E>E0
YII(x)=C e-ik‘x + D eik‘x
C=0, da keine Teilchen in (II) nach links fliegen
C=0 Æ (i) Æ (ii) ) ik(A-B)=-k‘ (A+B) )
11.4. Potentialstufe
Bereich (I): V(x)=0 )
E(x)
Stationäre Schrödingergleichung
(I)
YI(x)=A eikx + B e-ikx
|A|2
Bereich (II):
a2
YII(x)=C eax + D e-ax
E0
(II)
|D|2
|B|2
x
1.Y(x)
Auch
E>E0 wird ein Teil
der
reflektiert!
(Je mehr, je )höher E_0)
sollwenn
stetig differentierbar
auch
beiWelle
x=0 sein
(Randbedingung)
2. Wellenfunktion
YI(x=0)=YII(x=0)
) A+B=C+D
(i)
) ik(A-B)=-a(C-D) (ii)
9. Grundlagen der Quantenmechanik
Veranschaulichung der Potentialstufe mit Wellenpaketen:
Teilchen läuft mit doppelter Energie der Stufe auf die Stufe zu
ein klassisches Teilchen würde mit 1/2Ekin weiterlaufen!
Ort
E = ½ Ekin
Impuls
+ auf Stufe zu
- reflektiert
9. Grundlagen der Quantenmechanik
Veranschaulichung der Potentialstufe mit Wellenpaketen:
Teilchen läuft “bergab”: klassisch würde es beschleunigt weiterlaufen
9. Grundlagen der Quantenmechanik
Veranschaulichung der Potentialstufe mit Wellenpaketen:
Potentialstufe in 2 Dimensionen
Farbcode:
Farbe: Phase
Sättigung: Amplitude
(I)
E(x)
9. Grundlagen der Quantenmechanik
9.6. Der Tunneleffekt
(II)
E0
x
Idee: kann man die Welle “freisetzen”??
9. Grundlagen der Quantenmechanik
9.6. Der Tunneleffekt
(I)
(II)
(III)
YI(x)=A eikx + B e-ikx
E0
YII(x)=C eax + D e-ax
YIII(x)=A‘ eikx
0
x
a
Randbedingungen:
YI(0)=YII(0)
,
YII(a)=YIII(a)
Höhe 0.3eV, Breite 1nm
100
10-1
T
Transmissionskoeffizient (E<E0)
10-2
10-3
für aa >>1
(dicke Barriere)
10-4
0
0.05
0.1
0.15
ENERGY (eV)
0.2
0.25
0.3
9. Grundlagen der Quantenmechanik
9.6. Der Tunneleffekt
Transmission hängt ab von:
1. Barrierenhöhe (Exponentiell)
2. Barrierenbreite a
3. Masse
Makroskopisch irrelevant
9. Grundlagen der Quantenmechanik
9.6. Der Tunneleffekt
Ekin<E
Fragen:
1. Energieerhaltung ???
2. Wie lange braucht das Teilchen?
9. Grundlagen der Quantenmechanik
9.6. Der Tunneleffekt
9.6.1. Tunneleffekt Beispiel 1: Alphazerfall von Kernen
Alpha Zerfall: Pollonium
212Po
-> a + 208Pb + 8.78 MeV
He
Coulombabstossung
208Pb
1012 Tunnelwahrscheinlichkeit
Coulomb versus Kasten!
Kernkräfte
http://hyperphysics.phy-astr.gsu.edu/hbase/nuclear/alptun2.html#c1
9. Grundlagen der Quantenmechanik
9.6.1. Tunneleffekt Beispiel 1: Alphazerfall von Kernen
9.6.2. Tunneleffekt Beispiel 2: Rastertunnelmikroskop
•Verschiebung mit Piezos
3 Dimensional
•Dämpfung!!!
•Messung des Tunnelstroms
(wird konstant gehalten durch
Höhenvariation)
Elektronen in Metallspitze
quasi frei
Spitze
Wand: Potentialstufe
Substrat
a
0
Zwischenraum: Potentialbarriere
Zwischenraum
9. Grundlagen der Quantenmechanik
9.6.1. Tunneleffekt Beispiel 1: Alphazerfall von Kernen
9.6.2. Tunneleffekt Beispiel 2: Rastertunnelmikroskop
•Verschiebung mit Piezos
3 Dimensional
•Dämpfung!!!
•Messung des Tunnelstroms
(wird konstant gehalten durch
Höhenvariation)
9. Grundlagen der Quantenmechanik
9.7 Der (quantenmechanische) harmonische Oszillator
Potential:
Stationäre
Schrödingergleichung:
Klassische
Lösung: harmonische Schwingung
Oszillation zwischen Ekin und Epot
E(x)
Enn2
E0
9. Grundlagen der Quantenmechanik
9.7 Der (quantenmechanische) harmonische Oszillator
Potential:
Stationäre
Schrödingergleichung:
Klassische
Lösung: harmonische Schwingung
Oszillation zwischen Ekin und Epot
|Y(x)|2
Y(x)
Substituiere:
Lösung für C=1
E=1/2 ~ 
Gausskurve:
1. Tunnels in den klassich verbotenen Bereich
2. Maximale Aufenthaltswahrscheinlichkeit bei 0
(Hier ist klassisch ein Minimum!)
9. Grundlagen der Quantenmechanik
9.7 Der (quantenmechanische) harmonische Oszillator
Potential:
Stationäre
Schrödingergleichung:
Klassische
Lösung: harmonische Schwingung
Oszillation zwischen Ekin und Epot
|Y(x)|2
Y(x)
Substituiere:
Lösung für C=1
E=1/2 ~ 
Hermitesche Polynome
9. Grundlagen der Quantenmechanik
Harmonischer Oszillator:
1. Energieniveus äquidistant (~)
2. Nullpunkstenergie 1/2 (~)
Bohrsche Atom: En 1/n2
Kastenpotential:
En n2
9. Grundlagen der Quantenmechanik
Rayleigh, Jeans
Strahlungsgesetzt
Plancks Annahme: harmonischer Oszillator kann nicht
kontinuierlich absorbieren, sonder nur E= nh  diskret
9. Grundlagen der Quantenmechanik
Vergleich QM – Klassische Aufenthaltswahrscheinlichkeit
=20
=4
=0
9. Grundlagen der Quantenmechanik
Überlagerung von Zuständen 0,1
Ort
Impuls
Merke:
Grosse Auslenkung
Kleiner
mittleren
Impuls!
9. Grundlagen der Quantenmechanik
Kohärenter Zustand: Versuch den klassischen Oszillator nachzubilden
Gauss:
läuft NICHT ausseinander
(dank Potential)
Wellenpaket im Impuls und
Ortsraum
