1 11. Grundlagen der Quantenmechanik Klassische Mechnik

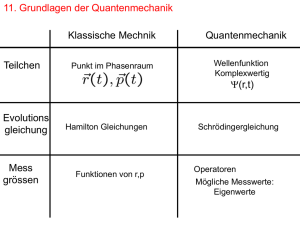
11. Grundlagen der Quantenmechanik
Klassische Mechnik
Teilchen
Quantenmechanik
Wellenfunktion
Komplexwertig
Punkt im Phasenraum
? (r,t)
Evolutions
gleichung
Mess
grössen
Hamilton Gleichungen
Funktionen von r,p
Komplexwertige Wellenfunktion ? (x,t)
Schrödingergleichung
Operatoren
Mögliche Messwerte:
Eigenwerte
Beispiel: deBroglie Ebene Welle
A(x,t) = A0 cos(kx - ? t)
Zeitabhängige Schrödingergleichung:
Für zeitunabhängiges Potential
Ansatz:
Imaginärteil
Wiederholung komplexe Zahlen:
x
?t
Realteil
Beobachtbar:
Vektorlänge
Unsichtbar:
Rotation mit t
1
Komplexwertige Wellenfunktion ? (x,t)
Beispiel: deBroglie Ebene Welle
A(x,t) = A0 cos(kx - ? t)
Zeitabhängige Schrödingergleichung:
Für zeitunabhängiges Potential
Ansatz:
Stationäre Schrödingergleichung
Allgemeiner Ansatz: ? (x)=Aeikx + B e -ikx
Beispiel 1: V(x)=0
löst:
Mit Zeitabhängigkeit:
Darstellung einer Ebenen Welle im Ort
Realteil
? (x) =
e ikx =
sin(x) + i cos(x)
-> |? (x)| 2 = const. = 1
Imaginärteil
Alternative Darstellung:
Farbkodierung der komplexen Zahlen
|? (x)|2 = const. = 1
moving-plane-wave-01_18a.mov
Graphik aus: Bern Thaller Visual Quantum Mechanics
http://www.kfunigraz.ac.at/imawww/vqm/index.html
2
Aufbau eines Wellenpaketes
? (x) = ? e ikx
d.h. die Phasengeschwindigkeit ist Energieabhängig -> Dispersion
Gauss-wellenpaket-aus-ebenen-wellen-03_02b.mov
Stationäre Schrödingergleichung
Beispiel 2: Unendlicher Potentialkasten
V(x)=
0 für 0·x¸L
1 sonst
? (x)=Aeikx + B e -ikx
? (x·0)=? (x¸L)=0
Randbedingung 1
? (x=0) = 0 ) A+B=0
) ? (x)=A(e ikx - e-ikx )=2iA sin(kx)
Randbedingung 2
? (x=L) = 2iA sin(kL) = 0
) kL= n? (n=1,2,3 ...)
Quantenzahlen n
Mögliche Energieniveaus in der Box:
Stationäre Wellenfunktionen in der Box:
3
Stationäre Schrödingergleichung
Bemerkungen:
• Unschärfe Relation Ort/Impuls
k= n? /L (n=1,2,3 ...)
• Nullpunktsenergie
• Woher kommt die Quantisierung??
• Zeitentwicklung der Zustände?
hängt von E n (n2) ab!
Mögliche Energienivieaus in der Box:
Stationäre Wellenfunktionen in der Box:
Real Imaginärteil
Aufenthaltswahrscheinlichkeit
http://www.quantum-physics.polytechnique.fr/en/stationary.html
4
Stationäre Schrödingergleichung
Bemerkungen:
• Unschärfe Relation Ort/Impuls
k= n? /L (n=1,2,3 ...)
• Nullpunktsenergie
• Woher kommt die Quantisierung??
• Zeitentwicklung der Zustände?
5) Was passiert wenn man
andere Energie, Wellenfunktion
erzwingt?
z.B. Barriere aufziehen?
Mögliche Energienivieaus in der Box:
Stationäre Wellenfunktionen in der Box:
Teilchen in 2 dim Potentialtopf
(k x , k y) = (0.86 , 0.5)
(? x , ? y) = (2? , 2? )
http://rugth30.phys.rug.nl/quantummechanics/potential.htm
5
Imagine a quantum particle initially described by a Gaussian wave
packet centered at the middle of a square box, with momentum
zero.
WAS PASSIERT??
11.4. Potentialstufe
Bereich (I): V(x)=0 )
(I)
? ?(x)=A
e ikx +
B
E(x)
Stationäre Schrödingergleichung
(II)
e-ikx
E0
Bereich (II):
?2
? ??(x)=C ei? x + D e -i? x
x
? (x) soll stetig differentierbar auch bei x=0 sein (Randbedingung) )
? I(x=0)=? II (x=0)
)
A+B=C+D
(i)
) ik(A-B)=-? (C-D) (ii)
6
11.4. Potentialstufe
Bereich (I): V(x)=0 )
E(x)
Stationäre Schrödingergleichung
(I)
(II)
? ?(x)=A e ikx + B e-ikx
E0
Bereich (II):
?2
? ??(x)=C ei? x + D e -i? x
x
? (x) soll stetig differentierbar auch bei x=0 sein (Randbedingung) )
? I(x=0)=? II (x=0)
)
A+B=C+D
(i)
) ik(A-B)=-? (C-D) (ii)
Fall a) E<E0
ik+?
ik-?
? ?reel ) C=0 weil sonst ? II(x!1) divergiert
C=0 Æ (i) Æ (ii) ) ik(A-B)=-? (A+B) )
Verhältnis von Ein- und Auslaufenden Teilchen:
11.4. Potentialstufe
Bereich (I): V(x)=0 )
E(x)
Stationäre Schrödingergleichung
(I)
? ?(x)=A
e ikx +
B
(II)
e-ikx
E0
Bereich (II):
?2
? ??(x)=C ei? x + D e -i? x
x
?• (x)Potentialwall
soll stetig differentierbar
reflektiert vollständig
auch bei x=0 sein (Randbedingung) )
• Wellenfunktion dringt in den klassisch verbotenen Bereich ein
? I(x=0)=? II (x=0)
) A+B=C+D
(i)
Energieerhaltung???
?) ik(A-B)=-?
E ? t > ~ (C-D) (ii)
Fall a) E<E0
? ?reel ) C=0 weil sonst ? II(x!1) divergiert
C=0 Æ (i) Æ (ii) ) ik(A-B)=-? (A+B) )
ik-?
ik+?
Verhältnis von Ein- und Auslaufenden Teilchen:
7
11.4. Potentialstufe
Bereich (I): V(x)=0 )
(I)
E(x)
Stationäre Schrödingergleichung
(II)
? ?(x)=A e ikx + B e-ikx
E0
Bereich (II):
?2
? ??(x)=C ei? x + D e -i? x
x
? (x) soll stetig differentierbar auch bei x=0 sein (Randbedingung) )
? I(x=0)=? II (x=0)
)
A+B=C+D
(i)
) ik(A-B)=-? (C-D) (ii)
Fall b) E>E0
klassisch: Teilchen fliegt mit verminderter Geschwindigkeit weiter
11.4. Potentialstufe
Bereich (I): V(x)=0 )
(I)
? ?(x)=A
e ikx +
B
E(x)
Stationäre Schrödingergleichung
(II)
e-ikx
E0
Bereich (II):
?2
? ??(x)=C ei? x + D e -i? x
x
? (x) soll stetig differentierbar auch bei x=0 sein (Randbedingung) )
? I(x=0)=? II (x=0)
)
A+B=C+D
(i)
) ik(A-B)=-? (C-D) (ii)
Fall b) E>E0
? ??(x)=C e-ik‘x + D eik‘x
C=0, da keine Teilchen in (II) nach links fliegen
C=0 Æ (i) Æ (ii) ) ik(A-B)=-k‘ (A+B) )
8
11.4. Potentialstufe
Bereich (I): V(x)=0 )
E(x)
Stationäre Schrödingergleichung
(I)
? ?(x)=A e ikx + B e-ikx
Bereich (II):
|A| 2
(II)
|D| 2
E0
|B| 2
?2
? ??(x)=C ei? x + D e -i? x
x
• Auch wenn E>E0 wird ein Teil der Welle reflektiert! (Je mehr, je höher E_ 0)
• Wellenfunktion
? I(x=0)=? II (x=0)
) A+B=C+D
(i)
) ik(A-B)=-? (C-D) (ii)
Fall b) E>E0
? ??(x)=C e-ik‘x + D eik‘x
C=0, da keine Teilchen in (II) nach links fliegen
C=0 Æ (i) Æ (ii) ) ik(A-B)=-k‘ (A+B) )
11.4. Potentialstufe
Bereich (I): V(x)=0 )
E(x)
Stationäre Schrödingergleichung
(I)
? ?(x)=A
e ikx +
B
e-ikx
|A| 2
Bereich (II):
?2
? ??(x)=C ei? x + D e -i? x
E0
(II)
|D| 2
|B| 2
x
• ? (x)
Auch
wenn
E>E
wird
ein
Teil
der
Welle
reflektiert!
(Je
mehr,
je
höher
E_
0
0)
soll stetig differentierbar
auch bei x=0 sein (Randbedingung) )
• Wellenfunktion
? I(x=0)=? II (x=0)
) A+B=C+D
(i)
) ik(A-B)=-? (C-D) (ii)
9
Wellenpaket, Potentialstufe
Klassisches Teilchen würde mit 1/2E kin weiterlaufen!
Ort
E = ½ Ekin
Impuls
+ auf Stufe zu
- reflektiert
gausspaket-auf-potentialstufe-mit-halber-energie07_06b.mov
Wellenpaket, Potentialstufe
BERGAB!
Klassisches Teilchen würde beschleunigt weiterlaufen!
gausspaket-potentialstufe-bergab07_06c.mov
10
Potentialstufe in 2 Dimensionen
Farbcode:
Farbe: Phase
Sättigung: Amplitude
gausspaket-2dim-potentialstufe-07_08a.mov
Stationäre Schrödingergleichung
(I)
E(x)
11.5. Tunneleffekt
(II)
E0
x
Idee: kann man die Welle “freisetzen”??
11
Stationäre Schrödingergleichung
(I)
11.5. Tunneleffekt
(II)
(III)
? ?(x)=A e ikx + B e-ikx
E0
? ??(x)=C ei? x + D e -i? x
?
???(x)=A‘
e ikx
0
x
a
Randbedingungen:
? I(0)=? II(0)
,
? II (a)=? III (a)
Höhe 0.3eV, Breite 1nm
100
10-1
T
Transmissionskoeffizient (E<E0)
10-2
10-3
für ? a >>1
(dicke Barriere)
Transmission hängt ab von:
• Barrierenhöhe (Exponentiell)
• Barrierenbreite
• Masse
10-4
0
0.05
0.1
0.15
0.2
0.25
0.3
ENERGY (eV)
Makroskopisch irrelevant
12
Ekin<E
Fragen:
• Energieerhaltung ???
• Wie lange braucht das Teilchen?
Wellenfunktion und Transmission als Funktion der Barrierenhöhe
(I)
(II)
(III)
E0
0
a
x
Tunnel-welle-durch-einstellbare-potentialstufe07_09d.mov
13
Tunneln eines Wellenpaketes
Überhöht
V = 2E, d = ?
http://rugth30.phys.rug.nl/quantummechanics/tunnel.htm#Potential%20barrier
Tunnels eines Gauss Wellenpaketes im Ortsraum
Mittlere Energie
des Wellenpaketes
Gausspaket-durch-barriere-07_11c.mov
14
Orts und Impulsraum:
Gausspaket-Tunnel-orts-impuls07_12c.mov
Mittlere Energie nahe an Schwellenhöhe
Durch Mehrfachreflexionen
wird ein Teil der Wellenfunktion
für einige Zeit unter der Barriere
gefangen
Gauss-tunnel-trapping07_12a.mov
15