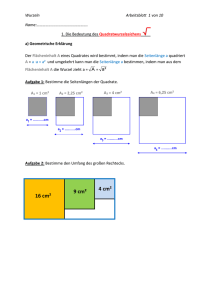
1. Die Bedeutung des Quadratwurzelzeichens

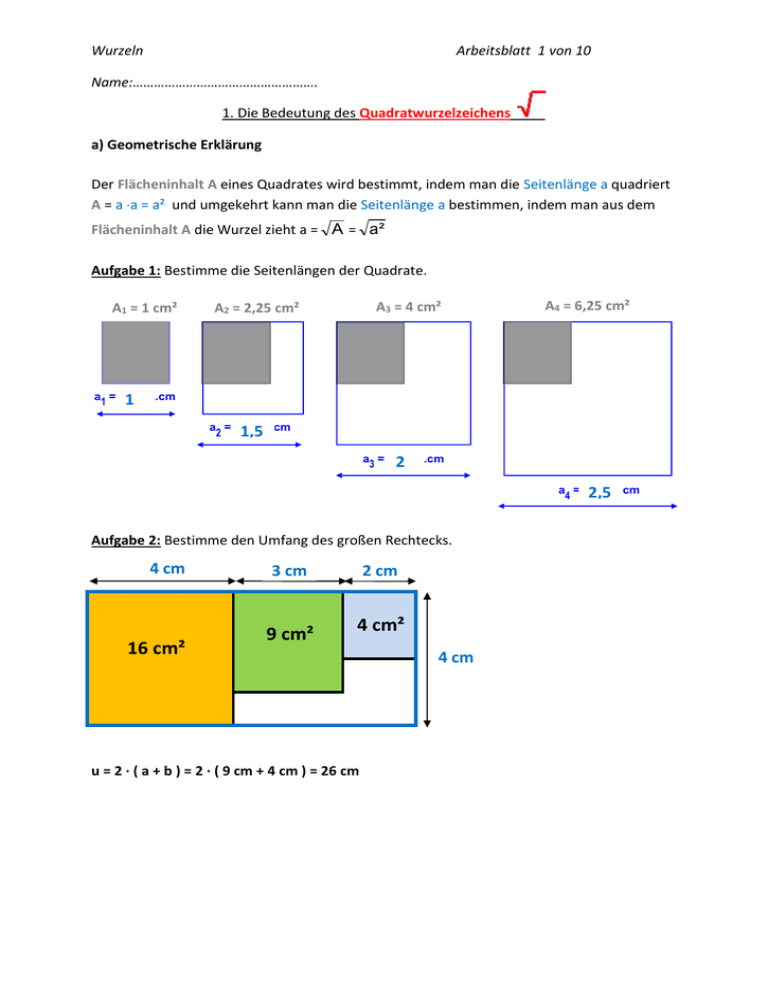
Wurzeln
Arbeitsblatt 1 von 10
Name:…………………………………………….
1. Die Bedeutung des Quadratwurzelzeichens
a) Geometrische Erklärung
Der Flächeninhalt A eines Quadrates wird bestimmt, indem man die Seitenlänge a quadriert
A = a a = a² und umgekehrt kann man die Seitenlänge a bestimmen, indem man aus dem
Flächeninhalt A die Wurzel zieht a = A = a ²
Aufgabe 1: Bestimme die Seitenlängen der Quadrate.
A1 = 1 cm²
cm
A3 = 4 cm²
cm
A2 = 2,25 cm²
cm
A4 = 6,25 cm²
cm
a = ............cm
1
1
a = ............cm
1,5
2
a3 = ............cm
2
a = ............cm
2,5
4
Aufgabe 2: Bestimme den Umfang des großen Rechtecks.
4 cm
16 cm²
3 cm
9 cm²
2 cm
4 cm²
u = 2 ∙ ( a + b ) = 2 ∙ ( 9 cm + 4 cm ) = 26 cm
4 cm
Wurzeln
Arbeitsblatt 2 von 10
Name:…………………………………………….
b) Arithmetische Erklärung
Zu jeder Rechnung (Rechenoperation) gibt es eine „Gegenrechnung“ (Gegenoperation), mit
der man die vorangegangene Rechnung wieder rückgängig machen kann.
Das Ziehen der Quadratwurzel ist die Gegenrechnung des Quadrierens
7 2  7  7  49
Aufgabe 3:
Ergänze die fehlenden Zahlen/Rechenoperationen in den leeren Kästchen.
3
3
-5
-2
∙5
15
+5
3
:5
hoch 2
3
9
3
49
7
36
6
0,04
0,2
0,25
0,5
hoch 2
7
hoch 2
6
hoch 2
0,2
hoch 2
0,5
 49  7
Wurzeln
Arbeitsblatt 3 von 10
Name:…………………………………………….
b) Mathematische Erklärung
Die Quadraturzel einer positiven Zahl a ist diejenige positive Zahl b, die mit sich selbst
multipliziert wieder a ergibt:
a  b  b2  b  b  a
Aufgabe 4: Bestimme die Quadratwurzeln:
144  12  12 12  144
0,25  0,5  0,5  0,5  0,25
2,25  1,5  1,5 1,5  2,25
4  2  22  4
9
3
3 3 9
25 
144
5
5 5


 25
12
12 12 144
11
4 2

0 0
1 1 1
 
2 2 4
 00  0
1  1  11  1
Achtung:
-1 


 1
Denn das Quadrat einer negativen Zahl ist immer eine positive Zahl!
Wurzeln
Arbeitsblatt 4 von 10
Name:…………………………………………….
2. Die n – te Wurzel einer Zahl
a) Geometrische Erklärung
Das Volumen V eines Würfels wird bestimmt, indem man die Kantenlänge a mit 3 potenziert
V = a a a = a³ und umgekehrt kann man die Kantenlänge a bestimmen, indem man aus dem
Volumen V die Wurzel zieht a = 3 V
b) Mathematische Erklärung
Die n-te Wurzel einer Zahl a ist diejenige Zahl b, die n mal mit sich selbst multipliziert wieder
a ergibt: n a  b  bn  b  b .... b  a
Also ist das Radizieren die Gegenrechnung des Potenzierens
25  2  2  2  2  2  32
 5 32  2
Aufgabe 5: Die 3. Wurzel
Bestimme die Kantenlängen und Volumina der Würfel, wenn der kleinste Würfel ein
Volumen von V = 27 cm³ hat.
V3 = 1728 cm³
V1 = 729 cm³
V1 = 27 cm³
a1 = 3 cm
a2 =9 cm
a3 =12 cm
Wurzeln
Arbeitsblatt 5 von 10
Name:…………………………………………….
Aufgabe 6: Bestimme die n-te Wurzel:
6
64  2
 2  2  2  2  2  2  64
5
1024  4
4
81  3
 4  4  4  4  4  1024
 3  3  3  3  81
3. Quadratwurzeln aus positiven Zahlen, die keine Quadratzahlen sind
Um Wurzeln von Zahlen zu bestimmen, die keine Quadratzahlen sind, verwendet man ein
Annäherungsverfahren. Dabei versucht man Dezimalzahlen zu finden, die gerade noch
kleiner oder größer wie die Wurzel dieser Zahl sind.
Aufgabe 7:
Gegeben sind folgende fünf „Dezimalzahlen“ :
1,4 ; 1,42 ; 1,415 ; 1,4142 ; 1,41421
Quadriere diese Zahlen mit dem Taschenrechner und überprüfe, ob sie größer oder kleiner
2 sind. Trage sie dann auf der richtigen Seite in den Zeilen ein.
2 < ………………..……
1,4 <
………………..…… <
2 < 1,42
………………..…… <
2 < 1,415
1,4142
<
2 < ………………..……
1,41421
<
2 < ………………..……
Durch Eingrenzung mit immer höherer Genauigkeit, kann man Quadratwurzeln aus positiven
Zahlen bestimmen, die keine Quadratzahlen sind. Jede dieser Eingrenzungen nennt man
Intervall. Das Verfahren nennt man Intervallschachtelung.
Wurzeln
Arbeitsblatt 6 von 10
Name:…………………………………………….
a) Quadratwurzeln mithilfe der Intervallschachtelung bestimmen
Aufgabe 8:
Versuche durch Probieren mit dem TR 2 Zahlen a und b zu finden für die gilt:
a² < 5 und 5 < b². Beginne mit natürlichen Zahlen.
Erhöhe bei jedem weiteren Durchgang die Genauigkeit um 1 Kommastelle.
0
1
2,0
2,1
2
3
2,2
2<
2;5
<3
2,2<
2;5
<2,3
2,23<
2;5
<2,24
2,236<
2;5
<2,237
4
2,3
2,4
2,20 2,21 2,22 2,23 2,24
2,230
2,231
2,232
2,233
2,234
b) Quadratwurzeln und Wurzeln höherer Ordnung mit dem TR bestimmen
Aufgabe 9:
Bestimme folgende Wurzeln mit dem Taschenrechner und notiere die Ergebnisse auf
2 Nachkommastellen.
3
3 = 1,73
30 = 5,48
300 = 17,32
10 = 3,16
100 = 10
200 = 14,14
10 = 2,15
Aufgabe 9:
4
10 = 1,78
5
10 = 1,58
1 Kästchen entspricht 1 cm²
Zeichnet man über der Diagonalen eines Quadrates ein weiteres Qadrat,
dann hat dies den doppelten Flächeninhalt!
Bestimme die Seitenlängen der 3 Quadrate gerundet auf
2 Stellen hinter dem Komma, wenn das kleinste Quadrat einen
Flächeninhalt von A = 5 cm² hat.
a1 = 2,24 cm a2 = 3,16 cm a3 = 4,47 cm
Wurzeln
Arbeitsblatt 7 von 10
Name:…………………………………………….
4. Rechenterme mit Quadratwurzeln – Wurzelgesetze
a) Addition und Subtraktion von Quadratwurzeln
Aufgabe 10:
Ein Kästchen in dieser Abbildung hat eine Seitenlänge von a = 1 cm und einen Flächeninhalt
von A = 1 cm².
a) A1 = 2 cm² ; A2 = 8 cm²; A3 = 16 cm²
b) a =
2 cm ; b = 8 cm und c = 4cm
c) a  2b  c  2  2 8  4
Die bisher verwendeten Rechengesetze und Umformungsregeln gelten auch für das Rechnen
mit irrationalen Zahlen und für das Umformen von Wurzeltermen.
Zusammenfassen gleicher Summanden
3 + 4 + 5 + 3 + 5 = 2∙3 + 2∙5 + 4 =20
2a + b + 3c + a + c = 3a + b + 4c
3  4  5  3  5 2 3  4 2 5
2 a  b 3 c  a  c 3 a  b 4 c
Aufgabe 10: Vereinfache so weit wie möglich.
4 2 + 3 8 - 2 2 = 2 2+ 3 8
3 a +8 b +5 a- b=8 a+7 b
3 a - ( 8 b + 5 a - b ) = -2 a -7 b
Gleiche Summanden kann man zu
einem Produkt zusammenfassen:
2x + 3x
= x ∙ (2+3)
= 5x
Wurzeln
Arbeitsblatt 8 von 10
Name:…………………………………………….
b) Multiplilation von Quadratwurzeln
Die Abbildung zeigt 4 Quadrate, deren Seiten
3 Rechtecke bilden. Die Seitenlängen der
Rechtecke kann man mit Wurzeln oder
Natürlichen Zahlen angeben.
Beispiel kleinstes Rechteck:
a = 2 cm oder a =
4 cm
und
b = 3 cm oder b = 9 cm
Ebenso kann man den Flächeninhalt des
kleinen Rechtecks auf 2 Arten berechnen:
A=
2 ∙ 3 cm² = 6 cm² und
A=
4 9
cm² = 36 cm²
Aufgabe 11:
Berechne die Flächeninhalte der beiden anderen Rechtecke ebenso auf 2 Arten:
A = 9 cm
∙
A = 3cm
∙
A = 16 cm ∙
A = 4 cm
∙
16 cm
4 cm
25 cm
5 cm
=
=
=
=
144 cm²
12 cm²
400 cm²
20 cm²
Regel:
Wurzeln werden multipliziert, indem man die Radikanden multipliziert und von dem Produkt
die Wurzel zieht.
Wurzeln
Arbeitsblatt 9 von 10
Name:…………………………………………….
Aufgabe 12: Ergänze.
4
9

9  16
16 

25

4

9


9
36

16

25
8

16
6
144

 12
400
 20
Aufgabe 13: Berechne.
2
8


2
16
4
3  12

3

12

36
2  50

2

50

100
6
 10
c) Division von Quadratwurzeln
Aufgabe 14: Berechne.
8
2
50
2


12
8

2
50
2
4
2
3
72

25
5
2


12
3
72
2

4

36
2
6
Wurzeln
Arbeitsblatt 10 von 10
Name:…………………………………………….
d) Teilweise die Wurzel ziehen
Kan man den Radikand so in ein Produkt zerlegen, dass ein Faktor eine Quadratzahl ist, kann
man aus diesem Faktor die Wurzel ziehen.
Aufgabe 9:
Zerlege den Radikand, wie im Beispiel, so in ein Produkt, dass ein Faktor eine Quadratzahl
wird und ziehe teilweise die Wurzel.
Beispiel:
12

4

20

4

5
2 5
50

25

2
5 2
72

36

2
6 2
3
2
3
e) Den Nenner „rationalmachen“
Bruchterme, in denen im Nenner eine Wurzel vorkommt, kann man vereinfachen, indem
man die Wurzel im Nenner beseitigt. Dies erreicht man durch Erweitern mit der Wurzel.
Aufgabe 10:
Beseitige die Wurzel im Nenner des Bruches durch Erweitern.
Beispiel:
3
3 3
3 3


 3
3
3
3 3
2
2 3
2


3
3
3 3 3
3
3 3
1


3
2 3 2 3  3 2
3  3 ( 3  3 )  3 3  3  3 3( 3  1)



 3 1
3
3
3
3 3