Dominik-2015-Gleichungslösen reloaded

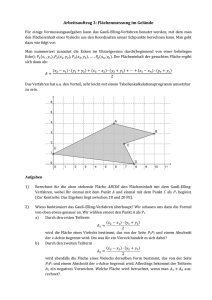
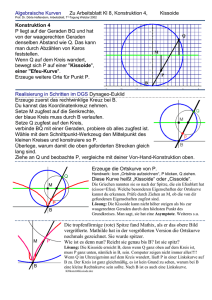
Gleichungslösen reloaded
Karl Josef FUCHS, Alfred DOMINIK, Universität Salzburg
0. Prolog
Vorab wollen wir als Autoren ein paar Worte über die Genese des provokanten
Titels unseres Beitrags verlieren. Mit diesem Titel, bewusst im Jargon unserer
Schülerinnen und Schüler gehalten, soll die Synthese aus traditionellem Stoff,
hier dem Lösen linearer Gleichungen in zwei Variablen und Neuer Technologie,
in unserem Fall der Einsatz von GeoGebra als Dynamische Geometriesoftware
([2], Didaktische Prinzipien, S. 16ff), benannt werden.
Vorgestellt wird eine Unterrichtssequenz aus der Sekundarstufe II mit der,
basierend auf der Software GeoGebra, grundlegende Konzepte der
Analytischen Geometrie auf explorative Weise für Schülerinnen und Schüler
sichtbar gemacht werden sollen. Bei der Planung und Durchführung des
Unterrichts finden zudem die grundlegenden didaktischen Prinzipien eines
gezielten Wechsels in der Repräsentation ([6], S. 2002, S. 87ff) sowie
Fundamentale Ideen eines zeitgemäßen Geometrieunterrichts ([4], 2007, S.
61ff) Berücksichtigung.
1. Die Lösung eines linearen Gleichungssystems als Urbild einer linearen
Abbildung
Eine erste Betrachtung zur Behandlung von linearen Gleichungssystemen in
zwei Variablen geht von der allgemeinen Schreibweise in der Analytischen
Geometrie aus. Ein lineares Gleichungssystem im ℝ2 wird demnach in der Form
𝑎11
𝐴 ∙ 𝑋 = 𝑏 mit 𝐴 = (𝑎
𝑎12
𝑥
𝑏1
𝑋
=
und
𝑏
=
),
(
)
(
) geschrieben werden.
𝑦
𝑏2
21 𝑎22
𝑥
𝑥+
𝑦= 3
3
1 1
Das Gleichungssystem
ist daher in (
) ∙ (𝑦) = ( )
−𝑥 + 4𝑦 = 7
−1 4
7
umzuschreiben. Bevor wir uns aber an den Computer setzen, wollen wir unsere
Aufgabe umformulieren und dabei den Begriff der Abbildung, eine universelle
Idee der Geometrie ([1], S. 199), ‚ins Spiel bringen‘.
Der Interpretation mittels Abbildung bedeutet also, dass wir das Bild eines
𝑥
3
Punktes (in unserem Beispiel 𝑃 = ( ) ) kennen und das Urbild 𝑋 = (𝑦)
7
suchen.
Öffnen wir das GeoGebra – Arbeitsblatt und tragen wir nun die freien Objekte
𝐴1 = (1,1), 𝐴2 = (−1,4), 𝑏 = (3,7) ein. Mit 𝑋 starten wir z. B. bei (2,2) und
beobachten die Werte sk1, sk2 der Produkte 𝐴1 ∙ 𝑋 bzw. 𝐴2 ∙ 𝑋. Stimmen sk1
und sk2 mit den Koordinaten von 𝑏 = (3,7) überein, so erhalten wir mit 𝑋 =
(1,2) das Urbild von 𝑃.
Abbildung 1: GeoGebra Arbeitsblatt
2. Basiskonzepte der Analytischen Geometrie werden sichtbar
2.1
Skalarprodukt und ‚Schatten‘ – Projektion als Fundamentale Idee
Wir verwenden nun die bekannte Darstellung des Skalarproduktes der


   
Vektoren a und b durch a  b = | a |  | b |  cos( ) , um den Wert des
Skalarproduktes als winkelabhängigen Flächeninhalt zu interpretieren.
Bezeichnet
den
Winkel
zwischen
den
Vektoren,
so



ergibt | b |  cos( ) bekanntlich den Wert der Projektion des Vektors b auf den

Vektor a .
Abbildung 2: Skalarprodukt von 2 Vektoren


Die Normalprojektion von b auf a ergibt die Länge der Projektion:
Abbildung 3: Normalprojektion
2.2
Skalarprodukt als Flächeninhalt

Indem wir den Vektor a um 90 Grad drehen und nur mehr seinen Betrag
betrachten, können wir den Wert des Skalarprodukts als Flächeninhalt des

Rechtecks mit den Seitenlängen „Projektion“ und | a | darstellen.
Abbildung 4: Skalarprodukt als Flächeninhalt

Zur besseren farblichen Unterscheidung wurden der Vektor a und sein Betrag
in der Abbildung mit roter Farbe dargestellt.
Um die Darstellung des Skalarproduktes als (winkelabhängigen) Flächeninhalt
zur Lösung linearer Gleichungen benutzen zu können, wird im Weiteren der

Vektor b als „xVektor“ bezeichnet.
Die Gleichung x + y = 3 als erste Gleichung des im 1. Abschnitt formulierten
Gleichungssystems wird nun so interpretiert, dass Werte für die x- und yKomponenten des xVektors gesucht werden, sodass sich der Wert 3 der
rechten Seite der Gleichung als Flächeninhalt aus dem Produkt der Länge des
 1
Koeffizientenvektors a    und der Länge der Projektion des xVektors auf
 2
den Koeffizientenvektor ergibt. Mit Hilfe von Schiebereglern für die
Komponenten des xVektors kann nun ein möglicher xVektor „experimentell“
bestimmt werden.
Abbildung 5: Lösen der Gleichung 𝑥 + 𝑦 = 3 als GeoGebra – Arbeitsblatt
Auch andere Werte für den xVektor lassen sich einfach bestimmen:
Abbildung 6: Lösen der Gleichung 𝑥 + 𝑦 = 3 als GeoGebra – Arbeitsblatt
Es lässt sich also auf geometrische Weise die bekannte Tatsache argumentativ
unterstützen, dass die Gleichung x + y = 3 unendlich viele „Lösungen“ für den
 x
xVektor=   erlaubt.
 y
Ein Problem bei der Darstellung des Skalarproduktes als Flächeninhalt ergibt
sich, wenn die „rechte“ Seite der linearen Gleichung einen negativen Wert
„trägt“, beispielsweise bei x + y = -3. Wir empfehlen in diesem Fall die
Multiplikation der Gleichung mit -1. Es ergibt sich –x – y = 3, der ursprüngliche
 1
   1
Koeffizientenvektor a    ändert sich zu a    . Das bedeutet, man
  1
1
verwendet das Konzept des Gegenvektors zu einem gegebenen Vektor um den
xVektor zu bestimmen. Nun kann wieder die oben beschriebene Strategie
verwendet werden, den xVektor durch Benützen der Schieberegler so zu
verändern, dass sich der Wert der rechten Seite der Gleichung als Maß für den
Flächeninhalt ergibt.
Interessant erscheint uns, dass der von uns als Koeffizientenvektor bezeichnete
Vektor der Normalvektor der durch die lineare Gleichung angegebenen
Geraden ist, somit erfolgt die Projektion nicht auf einen Richtungsvektor,
sondern auf einen Normalvektor der Geraden.
2.3 Lösen eines linearen Gleichungssystems
𝑥+
𝑦= 3
wird im GeoGebra - Arbeitsblatt nun
−𝑥 + 4𝑦 = 7
 1
   1
durch Eingabe der Koeffizientenvektoren a1    und a2    und
1
4
 x
Bestimmen des xVektors =   so gelöst, dass sich die rechten Seiten beider
 y
Das Gleichungssystem
Gleichungen als Flächeninhalte ergeben:
Abbildung 7: Lösen eines linearen Gleichungssystems als GeoGebra – Arbeitsblatt
Durch Benützung von Schiebereglern können bei diesem Arbeitsblatt sowohl
die Koeffizienten als auch die Werte der Skalarprodukte eingegeben werden.
Der Lösungsvektor wird automatisch generiert. Die Benützung der
Algebraansicht von GeoGebra ist bei der Benützung des Arbeitsblattes nicht
nötig und kann ausgeblendet werden.
Abbildung 8: Lösen eines linearen Gleichungssystems mit als GeoGebra - Arbeitsblatt
Das Arbeitsblatt erlaubt zudem die Visualisierung weiterer interessanter
Gesetzmäßigkeiten. Exemplarisch sei hier die Tatsache erwähnt, dass sich
bei Veränderung des ersten Skalarproduktes sk1 der Lösungsvektor auf

einer Geraden normal zum Koeffizientenvektor a2 bewegt.
Abbildung 9: Veränderung von sk1 bewegt den xVektor auf einer Geraden normal zum Vektor

a2
2.4 ‚Keine Lösung‘ (parallele Geraden) bzw. ‚unendlich viele‘ Lösungen
(idente Geraden)
𝑥+
𝑦= 3
besitzt- wie algebraisch leicht
2𝑥 + 2𝑦 = 5
gezeigt werden kann- keine Lösung.
Das Gleichungssystem
Eine visuelle Darstellung unterstützt diese Tatsache:
Abbildung 10: parallele Geraden
Im Geogebra – Arbeitsblatt zum Skalarprodukt stellt sich das Ergebnis „keine
Lösung“ in der Weise dar, dass der Lösungsvektor xVektor als „undefiniert“
ausgegeben wird.
Abbildung 11:parallele Vektoren ergeben einen undefinierten Lösungsvektor
Zum Studium der Lösungen identischer Geraden verwenden wir das GeoGebraArbeitsblatt aus Einheit 2.2.
Das Gleichungssystem
𝑥+
𝑦= 3
beschreibt zwei identische Geraden.
2𝑥 + 2𝑦 = 6
In unserer Betrachtungsweise handelt es sich um 2 Skalarprodukte mit
unterschiedlichen Koeffizienten und Ergebnissen.
Durch Verändern der Schieberegler bekommen wir mehrere Lösungen. Die
Endpunkte der Lösungsvektoren liegen auf der Geraden 𝑥 + 𝑦 = 3.
Abbildungen 12 -14 zeigen mögliche Lösungsvektoren für identische Geraden
 1
Man kann zudem erkennen, dass die doppelte Länge des zu a1    parallelen
1
  2
Koeffizientenvektors a2    einen verdoppelten Flächeninhalt ergibt.
 2
3. Kurzer abschließender Epilog
Genetisch wollen wir in unseren Unterrichtseinheiten als schülergerechtes
Entwickeln mathematischer Konzepte verstehen. Die Sinnfrage nach dem
‚Wozu braucht man das?‘ wird in diesem Unterrichtskonzept nicht durch eine
durchaus noch wünschenswerte Anbindung des Themas Gleichungslösen an
einen Realitätsbezug geleistet, sondern durch innermathematisches Experimentieren und Argumentieren bei gleichzeitiger Vernetzung mathematischer
Themengebiete, die von Schülerinnen und Schülern zu oft als disjunkt angesehen werden, eingelöst. Es ist dies eine Idee der Fachdidaktik, die keineswegs
neu ist (siehe Analyse zur Mathematikdidaktik von Helge Lenne ([5],1969), die
aber durch den Einzug neuer Technologien in den Mathematikunterricht
methodisch sinnvoll genützt werden kann.
Literatur
[1] Bender, P. & Schreiber, A.: Operative Genese der Geometrie. Schriftenreihe
Didaktik der Mathematik, Band 12, Wien, HPT und B. G. Teubner, Stuttgart,
1985
[2] Hohenwarter, M.: GeoGebra – didaktische Materialien und Anwendungen
im Mathematikunterricht. Dissertation zur Erlangung des Doktorgrades an der
Naturwissenschaftlichen Fakultät – Salzburg, 2006.
[3] Kautschitsch, H.: Erfolgreiche Bilder durch Neue Medien. In: Kadunz,
G. et al. (Hrsg.): Trends und Perspektiven. Wien: Verlag Hölder-Pichler-Tempsky,
S. 191-196, 1994.
[4] Krauthausen, G. & Scherer, P.: Einführung in die Mathematikdidaktik.
Heidelberg: Spektrum Akademischer Verlag, 3. Aufl., 2007.
[5] Lenne, H. (1969): Analyse der Mathematikdidaktik in Deutschland. Stuttgart:
Ernst Klett Verlag.
[6] Wittmann, E. Chr.: Grundfragen des Mathematikunterrichts. Braunschweig /
Wiesbaden: Vieweg verlag, 6. Aufl., 2002.