Nobelpreis_Physik_20..

Nobelpreis 2007
Entdeckung des
Riesenmagnetowiderstandes
Prof. Dr. H. Bärwolff:
Physik am Mittwoch
24.10.2007 1315 Raum 0.405
Der 23. Nobelpreis für Physik, 2007
geht an deutschen Forscher

2007 an P. Grünberg und A.
Fert

1988 am Forschungszentrum in
Jülich von Peter Andreas
Grünberg entdeckt
Agenda








Einführung
Physikalische Grundlagen
Erläuterung des GMR-Effektes
Anwendungen des GMR-Effektes
Java-Applet zur Anwendung
Ausblick (Spintransistor)
Lebenslauf des Nobelpreisträgers
Zusammenfassung
Grundlagen
Quantentheorie
 Maxwellsche Gleichungen
 Bändermodell (Fermi-Verteilungsfunktion)
 Mottsches Zweikomponentenmodell
 Bohr-Sommerfeld-Atommodell
 Festkörperphysik und Magnetismus

Spintronic
Spintronic = Spin + Elektronik
Definition:
Die Spintronic nutzt das magnetische
Moment des Elektrons zur Informationsdarstellung und –verarbeitung aus.
Spin






Spin
1920 durch Otto Stern und Walter Gerlach
entdeckt
spin engl.: Drehung, Drall
Quantenmechanische Eigenschaft von
Elementarteilchen
Beschreibt Eigendrehimpuls eines Teilchens
Messbar durch das von ihm assoziierte
magnetische Moment
Die Quantentheorie wurde 1899 von Max Planck entwickelt:
Der lineare harmonische Oszillator hat diskrete Energiestufen
Spin up
+ 1/2
Spin down
- 1/2
Die Theorie hat unübersehbare Konsequenzen:
Es gibt eine kleinste meßbare Wirkung, das Plancksche Wirkungsquantum h
E = h ƒ, Spin als quantenmechanischer Drehimpuls, HUR, etc.
Der Stern Gerlach Versuch
Maxwellsche Gleichungen
D
rotH  J 
t
B
rotE  
t
divD  
divB  0
Materialgleichungen:
J    j E
B  0  r H
D   0 r E
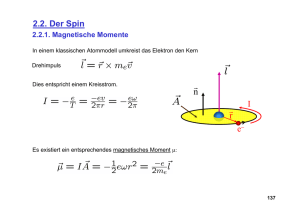
Bohrsches Magneton
Im Bohr-Sommerfeldschen-Atommodell
bewegen sich Elektronen auf Kreis- bzw.
Ellipsenbahnen um den Atomkern.
(4 Quantenzahlen: n, l, m, s) Pauli-Prinzip
M
r
e–
Ein Ringstrom I, der eine geschlossene
Fläche F umläuft erzeugt gemäß Maxwell
ein magnetisches Moment:
1
M  IF
c
J  LS
Bohrsches Magneton
 Das führt zum magnetischen Bahnmoment eines einzelnen Elektrons
B 
eh
 9,273 10  21  Gauß  cm 3
4   m  c
(Bohrsches Magneton)
Der Betrag des magnetischen Spinmoments nimmt mit
S 
1 h

2 2
ebenfalls genau den Wert des Bohrschen Magnetons an.
Magnetismus

Diamagnetismus

Paramagnetismus

Ferromagnetismus

Antiferromagnetismus

Ferrimagnetismus
Dia- und Paramagnetismus
B = μ0⋅H = μ0 ⋅ (H + M)
: = M / H
B: magnetische Flußdichte
H: magnetische Feldstärke
μ: Permeabilität (Durchlässigkeit) des Vakuums
M: Magnetisierung
: magnetische Suszeptibilität
<0
>0
Ferro-, Ferri-, und
Antiferromagnetismus
Ferromagnetismus
Ferrimagnetismus
Antiferromagnetismus
Fe, Co, Ni, Gd, Tb
Fe3O4
Speichermedium
MnO, FeO, CoO, NiO
Spins richten sich von selber aus, allerdings nur in den Weißschen Bezirken
Hysterese-Kurve
Remanenz
Koerzitivfeldstärke
Nicht magnetisierte Probe
Domänen willkürlich verteilt
Große Koerzitivfeldstärke, große Remanenz Dauermagneten
Bändermodell und Fermi-DiracVerteilungsfunktion
Fermi-Dirac-Verteilung
Bändermodell
Elektrischer Widerstand in Metallen

Drude-Lorentz-Modell

Komplexe Sreuphänomenologie
Elektron-Elektron-Streuung
Elektron-Phonon-Streung
Elektron-Gitterdefekte-Streuung
Spinabhängige Streuung (GMR)
Schrödingergleichung
Die Schrödingergleichung ist eine, bzw. die, zentrale
Grundgleichung der Quantenmechanik. Die Lösungen dieser
Gleichung werden auch Wellenfunktionen genannt.
Diese Wellenfunktionen beschreiben die räumliche und zeitliche
Entwicklung des Zustands eines Quantensystems.
Die Gleichung wurde 1926 von Erwin Schrödinger (1887-1961)
zuerst als Wellengleichung aufgestellt.
Als „Bewegungsgleichung der Quantenmechanik“ bildet sie noch
heute das Fundament für fast alle praktischen Anwendungen der
Quantenmechanik und Festkörperphysik.
Komplexwertige Wellenfunktion
Die komplexwertige Wellenfunktion ψ (r, t) eines Punktteilchens in
einem Potential V ist eine Lösung der Schrödingergleichung
 2


i  r ,t    
  V r ,t  r ,t 
t
 2m

wobei m die Masse des Teilchens, r sein Ort, Δ der LaplaceOperator und t die Zeit sind.
Sie ist eine lineare partielle Differentialgleichung 2. Ordnung,
parabolischer Typ, ähnlich der Wärmeleitungsgleichung
Kronig-Penney-Modell
Potentialschwelle
Der Festkörper als eindimensionale Näherung. In den
Potentialtöpfen wird die Schrödingergleichung gelöst. Orbitale
als Betragsquadrat einer Elektron-Wellenfunktion
(Aufenthaltswahrscheinlichkeit).
Riesenmagnetowiderstandseffekt
oder GMR-Effekt

1988 durch P. Grünberg und A.
Fert am Forschungszentrum Jülich entdeckt

1997 erste industrielle Anwendung durch die Fa.
IBM in Festplatten, Stuart Parkin
Magnetowiderstände

Definition
relative Änderung des Widerstands eines Leiters in
einem äußeren Magnetfeld
MR 



R
R
MR-Effekte
OMR: ordinary magnetoresistance
Lorentzkraft, tritt in allen Metallen auf
AMR: anisotropic magnetoresistance
Richtungsabhängiger Streuquerschnitt, verursacht durch
Spin-Bahn-Kopplung. Der Effekt ist abhängig vom Winkel
zwischen Stromfluss und äußerem Feld.
Riesen-Magnetowiderstand in ultradünnen
Schichten (Giant Magneto-resistance, GMR-Effekt)
GMR 
R
Ranti

Ranti  Rparallel
Ranti

Widerstandsänderungen
von 80% (300K) bzw. 220%
(4.2K)

Unabhänig von
Orientierung zwischen
Magnetfeld und Strom
Mottsches Zweistrommodell (MZM)
Durch inelastische
Elektron-Streuprozesse
kommt der Widerstand
zustande. Er ist der
ursächlichen Driftbewegung entgegengerichtet.
Gesamtstrom
M
Nach dem MZM (Sterne
markieren inelastische
Streuprozesse) teilt sich
der Gesamtstrom in zwei
Teilströme auf(Spinflip 0).
Parallele Ausrichtung
Antiparallele Ausrichtung
nicht magnetische
Schicht
Ferromagnetische
Schicht
Kanal für
Spin up/down
Ersatzschaltbild nach Kirchhoffschen Gesetzen
kleinen Widerstand
großen Widerstand
Ferromagnetismus
Spinpolarisiertes Bändermodell
Nettospinpolarisation P

J
P
J
 J   g   g  

0
 J   g   g  


Ji: Partiellen Ströme im Spin-Unterband
gi: Leitfähigkeit des Spin-Unterbandes
Für Ferromagneten gilt:
g  g
P ca. 10 – 45% für Fe, Co, Ni
Ladungs-/Spintransport


Strom besteht aus
Elektronen mit gleichen
Anteilen beider
Spinrichtungen
Transversales Magnetfeld

Ladungsträgerinjektion
aus (F) in (N)
 Überschuss einer Spinsorte

Zusätzlich Axiales
Magnetfeld
Der GMR-Effekt ist abhängig von:
Dicke der Schichten
 Temperatur
 Verwendete Materialien
 Weitere Einflußgrößen

Zwischenschichtkopplung




Keilförmige Schichtstruktur
Magnetische Schichten
Wechselwirken durch
Zwischenschicht
Quantenmechanischer Effekt
Räumliche Ausrichtung der
Magnetisierung
„oszillierende Zwischenschichtkopplung“
 Antiparallele Spinausrichtung automatisch
durch Schichtdicke einstellbar
Temperaturabhängigkeit



TEM-Aufnahmen von Co/Cu-Lagen
600°C Defekte im Schichtsystem
740°C granularer Zustand
Materialabhängigkeit
Material
GMR % (bei 300K)
{Fe(4,5)/Cr(12)}50
42
{Co(7,5)/Cu(9)}30
48
{Co(8)/Cu(8,3)}60
65
{Co(10)/Cu(10)}100
80
Co90Fe10(40)/Cu(25)/Co90Fe10(8)…
7
NiFe(100)/Cu(25)/Co(22)
4,6
Spin-Ventile
„free“ Ferromagnetische Schicht (NiFe)
nicht magnetische Schicht (Cu)
„pinned“ Ferromagnetische Schicht (NiFe)
Antiferromagnetische Schicht (FeMn)
AFM legt Magnetisierungsrichtung
der angrenzenden FM-Schicht fest
(pinning)
Erhöhung von H:
- nahe H = 0 schaltet free-FM
- Magnetisierung von pinned-FM bleibt
unverändert
 steiler Anstieg des Widerstands, da beide
FM-Schichten nun antiparallel sind
weitere Erhöhung von H:
- R bleibt solange hoch, bis äußeres Feld so
groß ist, dass die Austauschkopplung
(FM/AFM) überwunden wird
- Magnetisierung der zweiten, gepinnten
Schicht klappt um
 Widerstand fällt
Nanotechnologie in Computer-Festplatten
Leseköpfe von Festplatten

1997 von IBM entwickelt
und auf den Markt
gebracht

Heute Standardmäßig in
jeder Festplatte

Schnellere Lesezeiten

Leseköpfe sind kleiner
geworden  mehr Daten
auf Speichermedium
MRAM (Magnetische Speicher)





Information bleibt bei Stromunterbrechung erhalten
Lese/ Schreibzeit einige Nanosekunden  1000mal
schneller als herkömmliche Speicher
Verbrauchen weniger Energie als herkömmliche
Speicher
Werden durch Radioaktive Strahlung nicht zerstört
Höhere Speicherdichten (>30Gb/inch2) als
herkömmliche Medien (Auf CD-Größe ca. 500Gb)
Beschreiben eines Bit‘s:
-Elektrischer Puls  Magnetfeld
-Schreiben auf Schreib- und Lesebahn  Adressierung
einzelner Bits möglich
Lesen eines Bit:
- Widerstandsmessung
Bit 1  Strompuls der eine Drehung der Magnetisierung um
180° bewirkt (200 – 500ps)
Problem: Andere Zellen erfahren magnetische Anregung
durch Puls  langsames Abklingen  Totzeit 10ns
Bit 0  Pulse so wählen, dass Drehung um 360° stattfindet
GMR-Sensoren
Vorteile
 hohe Empfindlichkeit bei kleinsten
Abmessungen
 hohe Linearität und Temperaturstabilität
 gutes Preis-Leistungsverhältnis
Anwendungen von GMR-Sensoren



lineare Positionsmessung (z.B.
Druckkopfpositionierung)
Drehwinkelmessung
Drehzahlmessung (z.B. ABS)
Zukunftsaussichten
Quantenelektronik


Spin-Transistoren
Bauelemente mit einzelnen Elektronen/Atomen
Optoelektronik


Optische Datenverarbeitung
Holografische Speicher
Molekularelektronik

Moleküle und Atome als Schalter
Nanoelektronik

Als systemübergreifende Technologie
Zukunftsaussichten, GMR-Effekt
Magneto- und Spin-Elektronik


Spin-Transistoren
Konfigurierbare Logikbausteine denkbar
TMR: tunneling magnetoresistance



Wie GMR, jedoch Isolator als Zwischenschicht
MR durch spinabhängige Tunnelströme
R/R bis 50% in low-field Umgebungen
CMR: colossal magnetoresistance


Widerstandsänderungen um mehr als Faktor 1000!
Jedoch starke Magnetfelder und tiefe Temperaturen notwendig
Auf dem Weg zum Spin-Transistor
Der Rashba-Effekt


Ist eine bestimmte Kopplung des Elektronenspins in
Spin-Feldeffekttransistoren an die orbitale Bewegung
des Elektrons (asymmetrische hochreine HalbleiterHeterostrukturen bei tiefen Temperaturen)
Die Manipulation des Spins erfolgt durch eine Spannung,
die durch eine Gate-Elektrode gesteuert wird. Das
elektrische Feld steht senkrecht auf der Bewegungsrichtung des Elektrons und bewirkt eine
„Präzessionsbewegung“, die die Spinausrichtung
verändert (Spin-Orbit-Kopplung).
Lebenslauf des Nobelpreisträgers

Peter Andreas Grünberg wurde am 18. Mai 1939 in Pilsen (jetzt Tschechien)
geboren. Eltern Dipl.-Ing. Feodor A. Grünberg und Anna Grünberg

1946:
Aussiedlung nach Lauterbach in Hessen, Einschulung

1950-1959:
Besuch des Realgymnasiums Lauterbach

1959-1963:
Physikstudium an der Johann-Wolfgang-GoetheUniversität in Frankfurt (Main), Vordiplom 1962

1963-1969:
Fortsetzung des Physikstudiums an der Technischen
Hochschule Darmstadt, Diplom 1966, Promotion 1969

1966:
Heirat mit Helma Prausa. Drei Kinder: Andreas (1973),
Sylvia (1974) und Katharina (1981)

1969-1972:
Postdoctoral Fellow des National Research Council of
Canada an der Carleton Universität in Ottawa, Canada

seit 1972:
Wissenschaftlicher Mitarbeiter des Instituts für
Festkörperforschung im Forschungszentrum Jülich
Lebenslauf des Nobelpreisträgers

1984:
Habilitation an der Universität zu Köln, Privatdozent

1984-1985:
Forschungsaufenthalt am Argonne National
Laboratory, Illinois, USA

1986:
Arbeiten zur Antiferromagnetischen Kopplung in Fe-CrFe-Schichten

1988:
Arbeiten zum GMR-Effekt im Forschungszentrum
Jülich

1992:
Ernennung zum Außerplanmäßigen Professor an der
Universität zu Köln

1998:
Halbjähriger Forschungsaufenthalt an der Universität
von Sendai und im Forschungszentrum Tsukuba,
Japan

2004:
Nach 32 Jahren im Forschungszentrum Jülich tritt
Peter Andreas Grünberg in den "Unruhestand"
Literaturangaben












Mark Johnson, J. Phys. Chem. B 2005, 109, 14278 – 14291
Gary A. Prinz, Science, Vol. 282, 1998
H. W. Schumacher, Phys. Unserer Zeit, 6/2005 (36), 261
Jürgen Fassbender, Phys. Unserer Zeit, 3/2003 (34), 102
Heinz Krenn, Phys. Unserer Zeit, 5/2002 (33), 218 – 225
Wecker, Kinder, Richter, Phys. Unserer Zeit, 5/2002 (33), 210 – 217
Daniel Bürgler, Magnetoelectronics
Dennis Engberding, Giant Magnetic Resistance
P. Grünberg: Riesenmagnetowiderstand in magnetischen Schichtstrukturen,
Physikalische Blätter 51 (1995) Nr. 11
Gary A. Prinz: Spin-Polarized Transport, Physics Today, Special
Issue\Magnetoelectronics", April 1995
Rudolf Gross, Achim Marx: Spinelektronik, Skript zur Vorlesung, WaltherMeissner-Institut Garching, 2004
GMR-Animation, Forschungszentrum Jülich
http://www.fz-juelich.de/portal/gruenberg/hintergrund
Drittmittel- oder Applikationsforschung ist wichtig, aber
nicht alles. Grundlagenforschung bringt nicht das schnelle
Geld, sondern kostet zunächst Geld und erfordert einen
langen Atem. Das zahlt sich letztlich aus. Der Forscher
Grünberg ist dafür ein gutes Beispiel: bescheiden,
hartnäckig und geduldig.
Vielen Dank für Ihre
Aufmerksamkeit
(H. Bärwolff, A. Wagen)