Trigonometrische Funktionen (Seminararbeit).

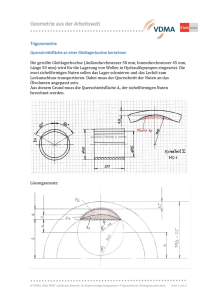
Trigonometrische
Funktionen
Inhaltlicher Überblick
Trigonometrie im Lehrplan
Geschichtlicher Hintergrund
Wdh.: Bogenmaß/ Winkelmaß
Einführungsmöglichkeiten
Sinus, Kosinus, Tangens im rechtwinkeligen
Dreieck
 Trigonometrische Funktionen
 Sinussatz, Kosinussatz





Lehrplan Realschule 10.Klasse
(6-stufig)
Lehrplaninhalt 5 Wochenstunden (Gruppe I):
Potenzen und Potenzfunktionen (ca. 14 Std.)
Exponential- und Logarithmusfunktionen (ca. 19 Std.)
Trigonometrie (ca. 52 Std.)
Abbildungen im Koordinatensystem (ca. 35 Std.)
= 120 Stunden
Lehrplaninhalt 4 Wochenstunden (Gruppe II/III):
Quadratische Funktionen (ca. 15 Std.)
Funktionen der indirekten Proportionalität und
Exponentialfunktionen (ca. 7 Std.)
Quadratische Gleichungen (ca. 20 Std.)
Raumgeometrie (ca. 19 Std.)
Trigonometrie (ca. 25 Std.)
= 86 Stunden
Trigonometrie
(aus dem Lehrplan 6-stufige Realschule, 5 WS)
• Definition von Kosinus, Sinus, Tangens
(ca. 10 Std.)
• Trigonometrische Funktionen (ca. 2 Std.)
• Berechnungen und Zusammenhänge (ca. 8 Std.)
• Berechnungen in Dreiecken (ca. 20 Std.)
• Skalarprodukt (ca. 12 Std.)
Geschichtlicher Hintergrund
Der Begriff Trigonometrie stammt aus
dem Griechischen und bedeutet
Dreiecksmessung.
Als Begründer der Trigonometrie gilt
Hipparch von Nicäa (um 160-125 v. Chr.).
Er war griechischer Astronom und
Geograph und gilt als Begründer der
Wissenschaftlichen Astronomie. Er lehnte
das heliozentrische (auf die Sonne als
Mittelpunkt bezogene) Planetensystem ab
und verbesserte das geozentrische (auf
die Erde als Mittelpunkt bezogene)
Planetensystem. Darüber hinaus schuf er
die Grundlagen für den ersten
Fixsternkatalog, den Ptolemäus und auch
Kopernikus im wesentlichen übernahmen.
Hipparch von Nicäa ist der Schöpfer der
Trigonometrie.
Ihre Weiterentwicklung verdankt sie
Ptolemäus von Alexandria (87-170 n. Chr.)
und später Mathematikern aus Indien und
dem arabischen Raum. Von dort kam sie
über Spanien wieder nach Europa, wo
Reglomontanus (1436-1476) in einem
Lehrbuch Winkelfunktionstafeln
veröffentlichte und mit dem Sinussatz
Flächenberechnungen durchführte.
Claudius Ptolemäus (87-170 n. Chr.), bedeutendster Geograph,
Mathematiker und Astronom der Antike. Er stellte die geographischen
Koordinaten von rund 350 Orten der damals bekannten Welt nebst den
mathematischen Methoden der Datengewinnung ebensozusammen wie
den ersten Fixsternkatalog. Seine Darstellung der Bewegung von
Himmelskörpern mit Hilfe von auf und ineinander abrollenden
Kugelschalen und Kreisen zementierte das geozentrische Weltbild für
rund 1500 Jahre.
Der französische Mathematiker Vieta (1540-1603)
schließlich gab dem Kosinussatz eine praktisch verwendbare
Form und begründete die Goniometrie (Winkelmessung).
Mittels der Trigonometrie gelingt die Verknüpfung von
Seitenlängen und Winkeln zur Berechnung der fehlenden
Stücke eines zunächst, aber nicht notwendig rechtwinkligen
Dreiecks, während man zuvor über den Winkelsummensatz
oder die Satzgruppe des Pythagoras nur Teilinformationen
erhalten konnte.
Durch die Ausweitung auf beliebige Ebenen und sogar
sphärische Dreiecke gewinnt die Trigonometrie vielfachen
Anwendungsbezug in Astronomie, Landvermessung und
Kartographie, im Bauwesen und in der Seefahrt. Die völlige
Lösung vom Dreieck führt zur Verwendbarkeit bei der
Beschreibung periodischer, das heißt sich in regelmäßigen
Zeitabständen wiederholender Vorgänge in Physik und
Technik, aber auch etwa in der Biologie.
Mathematik im Straßenverkehr
(oder beim Skifahren)
1. Zwei Verkehrsschilder:
a) Welche Bedeutung haben diese beiden
Schilder?
b) Zeichne zwei Straßen, an denen die
Verkehrsschilder
stehen könnten.
2. Verschiedene Steigungen
a) Wie sieht ein Weg mit 100 % (50 % bzw. 200 %) Steigung aus?
b) Welche Steigung hat ein Weg, der gegenüber der Horizontalen um
30°
(bzw. 60°) ansteigt?
c) Eine 2 km lange Straße steigt gleichmäßig mit 15 % Steigung an.
- Welcher Höhenunterschied wird dabei überwunden?
- Wie lang ist die Straße auf einer Landkarte mit dem Maßstab 1 :
100000?
3. Gefälle des Rheins
Straßburg liegt 140 m, Mainz 82 m über dem
Meeresspiegel.
a) Wie viel Prozent beträgt das durchschnittliche Gefälle des Rheins
zwischen
Straßburg und Mainz?
b) Informiere dich möglichst umfassend über die Städte Straßburg und
Mainz
und berichte deinen Mitschülern darüber.
4. Steigungen in Schottland
An einer Straße in Schottland
steht folgendes Verkehrsschild:
a) Welche Bedeutung hat wohl dieses
Schild?
b) Welcher Höhenunterschied wird auf
dieser Strecke überwunden?
5. Steigung und Neigungswinkel
Die Steigung s einer Straße hängt eng mit dem Winkel a zusammen,
den die Straße mit der Horizontalen einschließt. Stelle diesen
Zusammenhang grafisch dar.
6.Ein Weg um das Parkhaus
Ein Parkhaus besitzt die Gestalt
eines Zylinders. Es ist 25 m hoch
und hat einen Durchmesser von
30 m. Ein Zugangsweg soll in
Form einer gleichmäßig
ansteigenden Wendelstrecke rings
um das Parkhaus geführt werden,
sodass alle Parkdecks erreichbar sind.
Damit er auch für Rollstuhlfahrer
geeignet ist, darf er maximal 6 %
Steigung besitzen.
Ein Zeitschriftenartikel In der Zeitschrift „ADAC Motorwelt",
Ausgabe 12/2001, waren folgende Frage eines Lesers sowie
die Antwort der Redaktion abgedruckt:
• Bei Bergstrecken weisen Schilder auf die Steigung oder das Gefälle
hin. Wie steil sind
z. B. 15 % ?
Die Prozentangaben lassen sich mit einer einfachen Formel
umrechnen: Eine Steigung von - nur rein theoretisch möglichen - 100
% ergeben sich, wenn Sie nach einer zurückgelegten Strecke von 100
Metern einen Höhenunterschied von 100 Metern überwunden hätten.
Bei 15 % hätten Sie also nach 100 Metern Fahrt 15 Meter an Höhe
gewonnen. Übrigens: Besonders steile Passstraßen haben bis zu Z2 %
Steigung, Rampen in Tiefgaragen zirka 15 %.
Nimm zu diesem Zeitschriftenausschnitt Stellung und verfasse dazu
einen Leserbrief!