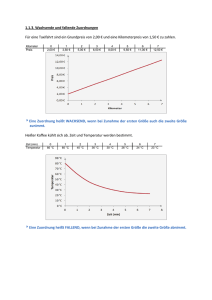
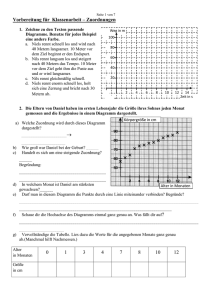
Funktionale Abhängigkeiten anschaulich machen

Funktionale Abhängigkeiten
anschaulich machen
Prof. Dr. Astrid Beckmann
PH Schwäbisch Gmünd
20.10.2006
• Ablauf
• Funktionale Abhängigkeit und Experimente
• Funktionale Abhängigkeiten
und die Aspekte des Funktionsbegriffs authentisch erfahren
• Bericht über die schulische Erprobung
• Was ist das Problem?
„Das Auto fährt
immer geradeaus.“
„Das Auto rollt
den Berg herunter.“
Beziehung zwischen x und y
y
x
„Die
Linie teilt das Koordinatensystem.“
Proportionale Funktion
y
x
• Gerade durch den Ursprung
• y/x = konstant
• Proportionale
Funktion
y
 konst
x
y
y
y0
x0
x
Funktionale Abhängigkeit
 jedem x ist genau ein y zugeordnet (Zuordnung)
 wenn x sich ändert, ändert sich auch y (Kovariation)
x
• Wie kann ein Verständnis für die
funktionale Abhängigkeit erreicht werden?
y
Strecke
Zeit
x
Realitätsbezüge
Authentische Erfahrungen!
 Experimente
• Zusammenhang zwischen Aspekten des
Funktionsbegriffs und Experimenten
• Zuordnung (einfache): Aufnahme von Einzeldaten
Beim Eintauchen eines Balls
mit einem bestimmten Radius
wird genau
ein bestimmtes Wasservolumen verdrängt.
Zuordnung: Jedem Radius – genau ein Wasservolumen
Die einfache Zuordnung wird handelnd erfahren.
• Zuordnung (kontinuierliche):
Aufnahme von verschiedenen Daten/ Messreihe
Jetzt wird nicht nur ein Ball betrachtet,
sondern (kontinuierlich der Reihe nach)
mehrere.
Der Radius wird jeweils
dem verdrängten Volumen zugeordnet.
Die kontinuierliche Zuordnung wird handelnd erfahren.
• Kovariation (diskrete)
Beispiel:
Zeit und Strecke, die ein Wagen in der Zeit fährt.
Gucken wir nach bestimmten Zeiten
auf die Uhr
,
stellen wir fest,
dass die gefahrene Strecke des Wagens
sich ebenfalls geändert hat.
Die diskrete Kovariation wird erfahren.
• Kovariation (kontinuierliche)
Jetzt gucken wir nicht immer erst nach bestimmten
Abständen auf die Uhr, sondern ständig.
Die Zeit läuft und gleichzeitig erleben wir, wie der Wagen
eine immer längere Strecke fährt.
Die kontinuierliche Kovariation wird erlebt.
• Objektaspekt
Der Objektaspekt umfasst den Zuordnungs- und den
Kovariationsaspekt. Er fasst die Funktion als Objekt,
als etwas Ganzes auf.
Dazu gehört:
- Beschreibung der Funktion durch ein Objekt, also
zum Beispiel durch eine Gleichung, einen Graphen usw.
- Das inhaltliche Erfassen dieses Objekts, also die Fähigkeit,
mit einer Funktionsgleichung wie y = ax
oder mit einem Namen wie ganzrationale Funktion die
entsprechende Zuordnung und Kovariation zu verbinden.
• Objektaspekt
Die Grenzen des Experiments motivieren dazu,
die Funktion als Objekt zu fassen.
Der Objektaspekt wird erfahren und erlebt.
• Experimente im Unterricht
Ziel: Funktionale Abhängigkeiten anschaulich machen
Das heißt u.a.:
• Funktionale Abhängigkeiten in Realitätsbezügen
diskutieren und erfahren
• Funktionale Abhängigkeiten authentisch erleben
• Die Aspekte Zuordnung und Kovariation während
der einzelnen Experimentierschritte bewusst machen
 Experimente mit Anregungen
• Realitätsbezug/ Impuls:
Wenn du die Wahl hast,
Fußball am Hang
oder auf einer ebenen Fläche zu spielen,
entscheidest du dich sicher für das Spiel auf der Ebene.
Offensichtlich verhält sich der Ball am Hang
und auf der Ebene unterschiedlich.
Tauscht euch in der Gruppe darüber aus.
Angenommen es steht nur ein hügeliges Gelände zur Verfügung
und der Ball rollt einen Hang herunter. Du rennst hinter dem Ball her
und willst ihn einholen.
Wie schnell musst du im Vergleich zum Ball rennen?
Beschreibe die Situation, bis du den Ball eingeholt hast.
Tauscht euch darüber in der Gruppe aus.
• Hypothesenbildung und Anregung zur
Prüfung
Allgemeine Aufgabe
Beschreibe den Zusammenhang
zwischen der beim Hinabrollen zurückgelegten Strecke
und der benötigten Zeit.
Überprüfe: Bestätigt der Zusammenhang eure obige Vermutung.
Beschreibe die besonderen Eigenschaften des Zusammenhangs.
• Authentisch erleben
Material:
• Kugel
• Maßband
• Stoppuhren
• Hang / Schiefe Ebene
zum Beispiel auf dem Schulhof
Es werden die Zeiten
für bestimmte Strecken gemessen,
die eine an einem Hang hinabrollende Kugel
für diese Strecken benötigt.
• Aspekt der (einfachen) Zuordnung
Lass die Kugel den Hang hinunter rollen.
Miss die Zeit, die sie für 4 m benötigt.
Trage den Messwert in das rechte Kästchen ein.
4m
• Aspekt der (kontinuierlichen) Zuordnung
Führe sechs weitere Messungen durch.
Trage die zusammen gehörenden Werte in die Tabelle ein.
Strecke s
in m
Zeit t
in s
0
0
1
1,7
4
3,7
9
5,5
15
7,4
• Aspekt der Kovariation
Betrachte die Tabelle.
Erkennst du besondere Zusammenhänge?
Betrachte das Schaubild.
Beschreibe es.
• Aspekt der Zuordnung
Betrachte das Schaubild.
Wie lange benötigt die Kugel für 15 m ?
• Aspekt der Kovariation
Wie verändert sich jeweils die Zeit, wenn du
die Kugel statt 2 m 4 m rollen lässt
und wenn du sie statt 7 m 9 m rollen lässt?
• Objektaspekt
Betrachte die Tabelle.
Gibt es eine Rechenvorschrift, mit der du aus der ersten
Größe stets die zugeordnete Größe ermitteln kannst
und die für möglichst alle Messwerte gilt?
Gib die Rechenvorschrift an.
Überprüfe die Funktionsgleichung mit Hilfe verschiedener
Messwerte.
Zeichne (mit dem CAS oder Grafiktaschenrechner) den
Graphen zu deiner Funktionsgleichung.
Vergleiche mit dem Graphen aus deinen Messwerten.
Allgemein:
• Kennenlernen der Bestandteile des Experiments
• Erkennen, welche Größen sich verändern lassen
• Auswählen zweier voneinander abhängiger Größen,
Hypothesenbildung
• Abhängigkeit beobachten: Verändern von x bewirkt Änderung von y
• Feststellen der funktionalen Abhängigkeit, y ist Funktion von x
• Erstellen einer systematischen Messreihe
• Auswerten, um welchen Funktionstyp es sich handelt (auch
qualitativ am Graphen)
• Untersuchen, welche Abhängigkeit interessiert, y = f(x) oder x = f(y)
• Ergebnisse für Voraussagen nutzen
Offene Aufgabenstellung:
In der Geschichte vom Froschkönig
fällt der Prinzessin ihre Kugel in den
Brunnen.
Um wie viel steigt der Wasserspiegel im
Brunnen, wenn die Kugel einen Radius von
6 cm hat und der Brunnen einen
Durchmesser von 1 m?
• Beispiele
Auftrag:
Bearbeiten Sie jeweils das Arbeitsblatt:
Lesen Sie die Texte und führen Sie die Aufträge aus.
Reflektieren Sie bitte ständig darüber,
an welchen Stellen die funktionalen Abhängigkeiten
besonders deutlich erfahren werden können.
Bitte führen Sie die Experimente
- so wie vorgesehen - auch wirklich durch!