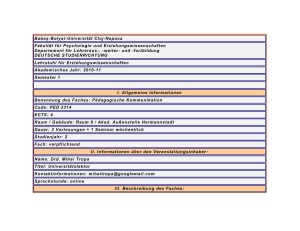
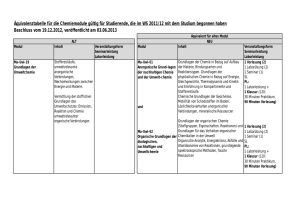
Document
Werbung

Fachhochschule Karlsruhe – Hochschule für Technik Fachbereich Informatik Intelligente Systeme Wissen aus Daten gewinnen Prof. Dr. Norbert Link Email: [email protected] http://www.iwi.hs-karlsruhe.de/~lino0001/ Intelligente Systeme - Inhaltsverzeichnis 1. Was leisten intelligente Systeme ? 4 Selbstexperimente Analyse der Selbstexperimente Beispielanwendungen 4 9 14 18 Intelligente Systeme und deren Aufgabe 2. Ein vereinfachtes System-Beispiel 22 Motordiagnose für Verbrennungskraftmaschine 3. Statistische Fundamente Bayes´sche Entscheidungstheorie Mehr als ein Merkmal Mehrere Merkmale, mehrere Klassen Entscheidungsfunktionen und –flächen Wie weiter ? 4. Entscheidungsflächen und –funktionen Vorlesung "Intelligente Systeme" 44 44 49 53 56 68 69 2 Intelligente Systeme - Inhaltsverzeichnis 5. Lineare Klassifikatoren Grundlagen Das Perzeptron Lineare Klassifikation nicht linear trennbarer Klassen Lineare Separierung von mehr als zwei Klassen Kleinste-Quadrate-Klassifikatoren Stochastische Approximation und der LMS Algorithmus 6. Nicht-lineare Klassifikatoren Mehrschicht-Perzeptrons Backpropagation-Algorithmus Netzgröße und –struktur Konvergenzverhalten und Beschleunigung Lernstrategien Alternative Kosten- und Aktivierungsfunktionen Vorlesung "Intelligente Systeme" 72 73 76 87 88 96 100 109 110 118 127 136 134 137 3 Intelligente Systeme - Inhaltsverzeichnis 7. Merkmalsvorverarbeitung und -auswahl Merkmalsvorverarbeitung Merkmalsbewertung und -auswahl 8. Merkmalserzeugung Hauptkomponententransformation Signalabtastung und Frequenzraumdarstellung 9. Einbringen von a priori Wissen Zeitdiskrete Prozesse: Hidden-Markov-Modelle Kausale Zusammenhänge: Bayesian Belief Networks Randbedingungen: Kostenfunktion-Regularisierung 10. Nicht-parametrische Klassifikatoren k-NN Klassifikatoren 140 141 146 156 157 165 174 175 185 192 197 198 11. Selbst-organisierende Karten Kohonen-Karten 203 204 Vorlesung "Intelligente Systeme" 4 1. Leistung intelligenter Systeme Vorschau über das Kapitel Selbstversuche Analyse der Selbstversuche Beispiel-Anwendungen Schlussfolgerungen aus den Beispielen Vorlesung "Intelligente Systeme" 5 1. Leistung intelligenter Systeme Intelligenz Intelligenz (lat.: intelligentia = "Einsicht, Erkenntnisvermögen", intellegere = "verstehen") bezeichnet im weitesten Sinne die Fähigkeit zum Erkennen von Zusammenhängen und zum Finden von optimalen Problemlösungen. Künstliche Intelligenz (KI) bezeichnet die mechanisch-elektronische Nachbildung menschlicher Intelligenz innerhalb der Informatik. Die KI findet zunehmend Einsatz in der ingenieurwissenschaftlichen oder medizinischen Technik. Mögliche Anwendungsszenarien sind: Optimierungsprobleme (Reiseplanung, Schienenverkehr), Umgang mit natürlicher Sprache (automatisches Sprachverstehen, automatisches Übersetzen, Suchmaschinen im Internet), Umgang mit natürlichen Signalen (Bildverstehen und Mustererkennung). Vorlesung "Intelligente Systeme" 6 1. Leistung intelligenter Systeme Selbstversuch 1 Hören Sie sich die folgenden Geräusche an. Was hören Sie ? Erstes Beispiel Musik Zweites Beispiel Ein Tier Drittes Beispiel Eine Maschine Vorlesung "Intelligente Systeme" 7 1. Leistung intelligenter Systeme Selbstversuch 2 Hören Sie sich die folgenden Geräusche an. Welches Musikinstrument hören Sie ? Erstes Beispiel Hammond-Orgel Zweites Beispiel Trommeln (Congas) Drittes Beispiel Elektrische Gitarre Vorlesung "Intelligente Systeme" 8 1. Leistung intelligenter Systeme Selbstversuch 3 Hören Sie sich die folgenden Geräusche an. Welches Tier hören Sie ? Erstes Beispiel Elephant Zweites Beispiel Affe Drittes Beispiel Flugzeug-Landeklappe Ihr Mustererkennungssystem wurde vermutlich durch eine falsche Erwartung getäuscht. Vorlesung "Intelligente Systeme" 9 1. Leistung intelligenter Systeme Selbstversuch 4 Hören Sie sich die folgenden Sounds an. Welchen Unterschied detektieren Sie ? Erstes Beispiel Zweites Beispiel Drittes Beispiel 500 rpm Propellerflugzeug 1200 rpm Vorlesung "Intelligente Systeme" 1800 rpm 10 1. Leistung intelligenter Systeme Selbstversuche Ergebnis In Begriffen der Mustererkennung haben Sie saubere Arbeit geleistet: 1) in Schall-Klassifikation und 2) in Größen-Schätzung aus Schallsignalen Letzteres haben Sie wahrscheinlich auch erkannt. Vorlesung "Intelligente Systeme" 11 1. Leistung intelligenter Systeme Analyse der Selbstversuche Was ist bei Ihnen vorgegangen ? Musik Tier-Geräusch Motor-Geräusch Schall- Druckquelle wellen Signal Ohr Nerven- Verarbeitung Klassensignal Im Gehirn zugehörigkeit Daten Vorlesung "Intelligente Systeme" Semantik 12 1. Leistung intelligenter Systeme Analyse der Selbstversuche Technologisches Äquivalent Objekt Geräusch Mikrophon Primär- Wandler signal (Sensor) El. Spannung Filter/Ampl. Spannung Sekundär- Signalauf- Sensorsystem signal bereitung Output rpm zu niedrig 0.06 Klasse 1 Wahrscheinlichkeit Klassifikator Mustererkennungsgerät rpm ok Klasse 2 0.92 Wahrscheinlichkeit rpm zu hoch Klasse 3 0.02 Wahrscheinlichkeit Vorlesung "Intelligente Systeme" 13 1. Leistung intelligenter Systeme Analyse der Selbstversuche Ein “rpm aus Geräusch” Klassifikator könnte so funktionieren: rpm zu niedrig Klasse 1 Klassifikator Mustererkennungsgerät rpm ok Klasse 2 rpm zu hoch Klasse 3 Vorlesung "Intelligente Systeme" 0.90 0.08 0.01 0.03 0.89 0.07 0.07 0.03 0.92 14 1. Leistung intelligenter Systeme Zusammenfassung unserer Selbstversuch-Erfahrung Wir haben das Vorliegen einer bestimmten Unterklasse aus einer möglichen Menge einer Oberklasse anhand eines Teilaspekts (Geräusch, Bild, …) festgestellt. Die Klassenzugehörigkeit ist mit Semantik verbunden. Das Ergebnis (Bestimmung der Unterklasse) hing ab von der Aufgabe (Vorgabe der Oberklasse). Die Aufgabe bestimmte somit die Menge der möglichen Unterklassen. Wird die Oberklasse falsch angegeben, sind die Ergebnisse i.A. falsch. Die Menge der Unterklassen war diskret oder kontinuierlich. Vorlesung "Intelligente Systeme" 15 1. Leistung intelligenter Systeme Beispiel-Anwendungen Dies war keine scharfe Definition, sondern nur ein Hinweis, was Mustererkennung sein könnte. Bevor wir zu systematischen Ansätzen übergehen, lernen wir noch etwas aus Beispielen. • Geschmack oder elektrochemische Potentiale • Spektren • Bilder • Symbolische Information Vorlesung "Intelligente Systeme" 16 1. Leistung intelligenter Systeme Beispiel-Anwendungen Geschmack oder elektrochemische Potentiale Soft drink Bier Ausprägung Merkmal xxxxxxxxxx xxxx Süße xxxxxx xxx Säure xxxxxxx Bitterkeit x x Schärfe x Geschmack ist die Antwort eines Nervs auf das chemische Potential µ bestimmter Substanzen. Kombinationen von µ-Sensoren werden genutzt, um das Vorhandensein und die Konzentration einer Menge von Substanzen zu festzustellen. Vorlesung "Intelligente Systeme" 17 1. Leistung intelligenter Systeme Beispiel-Anwendungen Signale Schallsignale: Spracherkennung, Maschinendiagn. A A “auf” w t t w “ab” A “Auswahl” “zurück” t w t w t A t t t Infrarotspektren: Gasmoleküle, pharmazeut. Produktion EKG/EEG: medizinische Diagnostik, HMI Chromatographie: Genanalyse Vorlesung "Intelligente Systeme" 18 1. Leistung intelligenter Systeme Spracherkennung Good morning ladies and gentlemen welcome to the show within the ability of the the million man had run in the middle of the city’s the law and some run for the moment I want I knew Vorlesung "Intelligente Systeme" 19 1. Leistung intelligenter Systeme Beispiel-Anwendungen Verifikation der Personen-Identität Bilder 1. Identifikation (mittels Name oder Magnetkarte) 2. Schnappschuss des Gesichts 3. Extraktion eines Merkmalsmusters 4. Abruf des Merkmalsmusters der Person aus Datenbank 5. Vergleich der Muster 6. Schwellwert: Erkennung Korrelation c Wenn c > Schwelle, dann Identität ok Vorlesung "Intelligente Systeme" 20 1. Leistung intelligenter Systeme Gesichtsdetektion Vorlesung "Intelligente Systeme" 21 1. Leistung intelligenter Systeme Beispiel-Anwendungen Symbolische Information Kundenprofile Ausprägung Ausprägung xxxxxxxx xxx x xxxx xxx x x xxxx x xxxxx gut Vorlesung "Intelligente Systeme" M1 M2 M3 M4 M5 Merkmal Klasse M1 M2 M3 M4 M5 Merkmal Merkmale M1: Wert pro Einkauf M2: Jährliche Einkäufe M3: Reklamationen M4: Zahlgeschwindigkeit M5: Akquisitionsaufwand schlecht 22 1. Leistung intelligenter Systeme Intelligente Systeme und deren Aufgabe Ein „intelligentes System“ Die Eingabe kann aus verschiedenen Das intelligente System kann Quellen kommen. verschiedene Aufgaben haben. W3 Syntaktischer Analysator Wert einer linguistischen Variablen Name Estimator Wert einer „physikalischen“ Variablen Wert kont. Klassifikator Klassenzugehörigkeit Wert diskret Mustererkennungs-Apparat Vorlesung "Intelligente Systeme" Die Ausgabe kann unterschiedlicher Art sein. 23 1. Leistung intelligenter Systeme Intelligente Systeme und deren Aufgabe Erste Aufgabe eines intelligenten Systems: Informationsgewinnung Gj+nj M+nM p3 Klasse wj Gk+nk Klasse wk m1 p1 m2 p2 Gl+nl Klasse wl p4 Abbildung 1 Beschreibungs(Zustands-)raum C m3 Abbildung 2 Zugänglicher Musterraum P Beobachtungs- oder Meßraum F Informationsgewinnung Vorlesung "Intelligente Systeme" 24 1. Leistung intelligenter Systeme Zweck intelligenter Systeme: Situationserkennung Erste Stufe in der Interaktion mit Objekten Interaktion mit Objekten: Reaktion und Beeinflussung Erste Situationserkennungs-Aufgabe: Identifikation 1. Identifiziere die Klasse eines Objekts anhand eines Teilaspekts 2. Stelle den Zustand bzw. die aktiven Methoden anhand einer Äußerung des Objekts fest. Folgeaktionen: Rufe aus einer Datenbank alle für eine Reaktion bzw. Beeinflussung nötigen Aspekte der Klasse ab: • Reaktion: Ablauf der aktiven Methode, Aktivitäten des aktuellen Zustands • Beeinflussung: Menge und Aufruf der Methoden, mögliche Zustände und Zustandsübergänge Vorlesung "Intelligente Systeme" 25 1. Leistung intelligenter Systeme Zeck intelligenter Systeme: Situationserkennung Zweite Situationserkennungs-Aufgabe: Verhaltensmodellierung Modellierung (Nachahmung) von Methoden eines unbekannten Objekts (z.B. Experte oder Prozess) 1. Angebot von Daten und Signalen, Aufzeichnen der Reaktion 2. Erlernen des Zusammenhanges 3. Anwendung Aus verfügbaren (beobachtbaren, unvollständigen und gestörten) Daten optimale Entscheidung treffen ! Vorlesung "Intelligente Systeme" 26 2. Ein Beispiel Motordiagnose für Verbrennungskraftmaschinen Beobachtbare Größe: Signal des Drehzahlgebers Diagnoseleistung (ohne zusätzliche Sensorik) Zündaussetzer, Verbrennungsstörung Einspritzung Ventilundichtigkeit “Blow-by” (undichter Kolbenring) Reibung Vorlesung "Intelligente Systeme" 27 2. Ein Beispiel Motordiagnose für Verbrennungskraftmaschinen Zündung Einspritzung Uind Dichtheit Reibung t Induktionssensor Die Vorgänge im Motor verursachen Änderungen der Winkelgeschwindigkeit. Motor Vorlesung "Intelligente Systeme" Zahnrad 28 2. Ein Beispiel Motordiagnose für Verbrennungskraftmaschinen Zündaussetzer-Erkennung Komponente 1 Winkelgeschwindigkeit eines Zyklus InduktionsSensor Vorlesung "Intelligente Systeme" 29 2. Ein Beispiel Motordiagnose für Verbrennungskraftmaschinen Zündung Einspritzung Dichtheit Uind T Berechenbar aus Beobachtung: Wechselanteil des Drehmoments 2 1 , M N Zähne T Induktionssensor Motor Zahnrad Nettodrehmoment [Nm] [Nm] Wechseldrehmoment Reibung t Normalbetrieb Zündaussetzer 1.000 500 0 -500 -1.000 0 120 240 360 480 600 Kurbelwinkel [Grad] Wechseldrehmoment eines 6-Zylinder-Motors Vorlesung "Intelligente Systeme" 30 720 2. Ein Beispiel Motordiagnose für Verbrennungskraftmaschinen Zündaussetzer-Erkennung Komponenten 2 und 3 Winkelgeschwindigkeit eines Zyklus InduktionsSensor Periode T Bestimmung Vorlesung "Intelligente Systeme" Drehmoment Berechnung 31 2. Ein Beispiel Motordiagnose für Verbrennungskraftmaschinen Wechseldrehmoment [Nm] Zündaussetzer-Erkennung Normalbetrieb 1.000 500 M5 M4 M3 M2 M1 Zündaussetzer M6 0 Charakteristisch: Drehmoment-Maxima M1, …, M6 der einzelnen Zylinder. -> Bestimmung der Maxima (Merkmale) -500 -1.000 0 f1 120 f2 240 360 480 f3 f4[Grad] Kurbelwinkel f5 600 f6 720 Bem.: Phasenwinkel fi char. Einspr. Betrachte nur Zylinder 4: Messungen von M4 für Normalbetrieb (Klasse c1) und Zündaussetzer (Klasse c2): Stichprobe Vorlesung "Intelligente Systeme" 32 2. Ein Beispiel Motordiagnose für Verbrennungskraftmaschinen Zündaussetzer-Erkennung Komponente 4 Winkelgeschwindigkeit eines Zyklus InduktionsSensor Periode T Bestimmung Drehmoment Berechnung Merkmalsextraktion: Drehmomentmaxima Vorlesung "Intelligente Systeme" 33 2. Ein Beispiel Motordiagnose für Verbrennungskraftmaschinen Zündaussetzer-Erkennung Vorkommensanzahl Betrachte nur Zylinder 4: Messungen von M4 für Normalbetrieb (Klasse c1) und Zündaussetzer (Klasse c2): Stichprobe aus vielen Umdrehungen. Bilde das Histogramm der Drehmomentwerte der Stichprobe: 1600 1400 Zündaussetzer 1200 Normal 1000 800 600 400 200 0 0-100 100200 200300 300400 400500 500600 600700 700800 Vorlesung "Intelligente Systeme" 800- 900900 1000 Wechseldrehmoment 34 2. Ein Beispiel Motordiagnose für Verbrennungskraftmaschinen Zündaussetzer-Erkennung Wähle aufgrund des Histogramms der Drehmomentwerte der Stichprobe den geeignetsten Schwellwert (mit dem kleinsten Fehler) zur Entscheidung über die Klassenzugehörigkeit: normal Vorkommensanzahl Zündaussetzer 1600 1400 Zündaussetzer 1200 Normal 1000 800 600 400 200 0 0-100 100200 200300 300400 400500 500600 600700 700800 MT Vorlesung "Intelligente Systeme" 800- 900900 1000 Wechseldrehmoment 35 2. Ein Beispiel Nebenbemerkung Histogramm und Wahrscheinlichkeitsdichte Wahrscheinlichkeitsdichte: relative Häufigkeit pro Intervall x x x x xxxx x x xx x x 70 Histogramm: Teile die Größe x in Intervalle mit Breite Dx. Zähle Anzahl in jedem Intervall. x 20 x x x x x xxxx x x xx x x 70 Trage die Anzahl gegen das Intervall auf. 15 10 x 5 x 20 0 Stichprobe: Führe N Versuche aus, miss jedes mal die Größe x. Vorkommensanazahl (frequency) k Histogramm von x x 20 30 40 50 60 Stichprobe mit 50 Versuchen Vorlesung "Intelligente Systeme" 36 70 2. Ein Beispiel Nebenbemerkung Histogramm und Wahrscheinlichkeitsdichte x 20 30 40 50 60 70 0.06 0.04 0.02 0.00 Wahrscheinlichkeitsdichte 15 10 5 0 Vorkommensanazahl (frequency) k Wahrscheinlichkeitsdichte r: relative Häufigkeit pro Intervall = (Vorkommensanzahl/Stichprobenumfang)/Intervallbreite = (k/N)/Dx = relative Häufigkeit / Intervallbreite = h/ Dx Histogram von x Histogramm von x x 20 30 40 50 60 70 W-Dichte = (7/50) / 5 = 0.028 Vorlesung "Intelligente Systeme" 37 2. Ein Beispiel Nebenbemerkung Histogramm und Wahrscheinlichkeitsdichte Histogramm von x 20 30 40 50 60 70 Density 0.02 x 0.00 0.02 0.04 0.04 0.06 Histogramm von x 0.00 Wahrscheinlichkeitsdichte r Mit zunehmender Stichprobengröße Balkenbreite immer kleiner, so dass im unendlichen Fall die Balkenbreite unendlich klein. 20 30 40 50 60 70 80 S Wahrscheinlichkeitsdichten x Balkenbreiten = 1 Vorlesung "Intelligente Systeme" 38 2. Ein Beispiel Nebenbemerkung Körpergröße nach Geschlecht (D, über 18a) Vorlesung "Intelligente Systeme" Größe F M <150 cm 0,6% 0,1% 150-154 cm 4% 0,1% 155-159 cm 12,7% 0,3% 160-164 cm 27% 2,3% 165-169 cm 29,1% 9% 170-174 cm 17,6% 19,2% 175-179 cm 6,9% 26,1% 180-184 cm 1,8% 23,9% 185-189 cm 0,2% 12,8% >190 cm <0,1% 6,3% 39 2. Ein Beispiel Nebenbemerkung Körpergröße nach Einkommen (D, über 18a) Vorlesung "Intelligente Systeme" 40 2. Ein Beispiel Nebenbemerkung Körpergröße nach Bundesland (D, über 18a) Vorlesung "Intelligente Systeme" 41 2. Ein Beispiel Auffinden der Schwelle mittels Histogramm-Auswertung (1) Wahrscheinlichkeitsdichten des Merkmals M für Zündaussetzer pZ(M) und Normalbetrieb pN(M) mit a priori Auftrittswahrscheinlichkeiten von Zündaussetzern PZ und Normalbetrieb PN. Bedingung PZ + PN = 1. Ergibt Gesamtwahrscheinlichkeitsdichte p(M) = PZ pZ(M) + PN pN(M) Im Gauss´schen Fall: p( M ) PZ e 2 Z ( M Z )2 2 Z 2 PN e 2 N ( M N )2 Vorlesung "Intelligente Systeme" 2 N 2 42 2. Ein Beispiel Auffinden der Schwelle mittels Histogramm-Auswertung (2) Gaussfunktion: Wahrscheinlichkeitsdichtefunktion der Normalverteilung „Vorurteilsfreieste“ Annahme einer Wahrscheinlichkeitsdichtefunktion, wenn nur der Mittelwert und die Varianz 2 bekannt sind. Wahrscheinlichkeitsdichtefunktion von unendlich vielen Summenvariablen. 1 2 p ( x) 1 e 2 ( x )2 2 2 Gesamtfläche = 1 Fläche zwischen und ungefähr 2/3 Fläche zwischen 2 und 2 ungefähr 95% Graphik aus Duda, Hart, Stork: Pattern Classification 2nd edition, Wiley-Interscience Vorlesung "Intelligente Systeme" 43 2. Ein Beispiel Auffinden der Schwelle mittels Histogramm-Auswertung (3) Wahrscheinlichkeit einer Fehlzuordnung E: E ( M T ) PN MT p N ( M )dM PZ PZ MT p Z ( M )dM Minimierung von E dE ( M T ) dM T M ~ ~ ! 0 PZ pZ ( M T ) PN p N ( M T ) T ~ MT Einsetzen, logarithmieren und vereinfachen ergibt quadratische Gleichung ~ 2 ~ A MT B MT C 0 mit A Z2 N2 ; B 2( Z N2 N Z2 ); C N2 Z2 Z2 N2 2 Z2 N2 ln Vorlesung "Intelligente Systeme" N PZ Z PN 44 2. Ein Beispiel Auffinden der Schwelle mittels Histogramm-Auswertung (4) Vorgehen nach obiger Methode: 1. 2. 3. 4. 5. 6. Trainingsstichprobe Datenmaterial mit Merkmalswerten Histogramm für Zündaussetzer hZ Histogramm für Normalbetrieb hN Berechnung von Z und Z aus hZ Berechnung von N und N aus hN Berechnung von A, B und C: A Z2 N2 ; B 2( Z N2 N Z2 ); C Z2 N2 N2 Z2 2 Z2 N2 ln N PZ Z PN 7. Berechnung der Schwelle durch Lösung der quadratischen Gleichung ~ 2 ~ A MT B MT C 0 8. Anwenden der Schwelle auf neues Datenmaterial Vorlesung "Intelligente Systeme" 45 2. Ein Beispiel Motordiagnose für Verbrennungskraftmaschinen Zündaussetzer-Erkennung Komponente 5 und Gesamtsystem Winkelgeschwindigkeit eines Zyklus InduktionsSensor Periode T Bestimmung Merkmalsextraktion: Drehmomentmaxima Drehmoment Berechnung Klassifikation: Anwendung Optimaler Schwellwert Normal Vorlesung "Intelligente Systeme" Zündaussetzer 46 2. Ein Beispiel Auffinden der Schwelle mittels Histogramm-Auswertung (5) Vorgehen nach obiger Methode: 1. Trainingsstichprobe Datenmaterial mit Merkmalswerten Drehmoment Klasse Drehmoment Klasse 400 Z 800 N 500 Z 750 N 300 Z 800 N 500 Z 800 N 500 Z 800 N 400 Z 850 N 600 Z 850 N 700 Z 800 N 500 Z 800 N 600 Z 750 N 500 Z 750 N 700 N 800 N 750 N 900 N 800 N 850 N 850 N Vorlesung "Intelligente Systeme" 47 2. Ein Beispiel Auffinden der Schwelle mittels Histogramm-Auswertung (6) Vorgehen nach obiger Methode: 2. Histogramm für Zündaussetzer hZ 3. Histogramm für Normalbetrieb hN Drehm. Kl. Drehm. Kl. 400 Z 800 N 500 Z 750 N 8 300 Z 800 N 7 500 Z 800 N 500 Z 800 N 400 Z 850 N 5 600 Z 850 N 4 700 Z 800 N 500 Z 800 N 3 600 Z 750 N 2 500 Z 750 N 1 700 N 800 N 750 N 900 N 800 N 850 N 850 N h[1/11] h[1/18] 6 Z N M 0 300 400 500 600 700 800 900 1000 Vorlesung "Intelligente Systeme" 48 2. Ein Beispiel Auffinden der Schwelle mittels Histogramm-Auswertung (7) Vorgehen nach obiger Methode: 4. Berechnung von Z und Z aus hZ h[1/11] h[1/18] 8 L xi h( xi ) 7 i 1 6 L ( xi ) 2 h( xi ) 2 5 i 1 Z N 4 3 2 L Z M Z i h( M Z i ) 1 i 1 M 0 300 400 500 600 700 800 900 1000 L Z ( M Z i ) 2 h( M Z i ) 2 1 300 1 400 2 500 5 600 2 700 1 11 500 i 1 1 12 (300 500) 2 1 (400 500) 2 2 (500 500) 2 5 (600 500) 2 2 (700 500) 2 1 (100) 2 11 11 Vorlesung "Intelligente Systeme" 49 2. Ein Beispiel Auffinden der Schwelle mittels Histogramm-Auswertung (8) Vorgehen nach obiger Methode: 5. Berechnung von N und N aus hN h[1/11] h[1/18] 8 L xi h( xi ) 7 i 1 6 L ( xi ) 2 h( xi ) 2 5 i 1 Z N 4 3 2 L N M N i h( M N i ) 1 i 1 M 0 300 400 500 600 700 800 900 1000 5 N ( M N i ) 2 h( M N i ) 2 1 700 1 750 4 800 8 850 4 900 1 18 800 i 1 1 2 (700 800) 2 1 (750 800) 2 4 (800 800) 2 8 (850 800) 2 4 (900 800) 2 1 (100) 2 18 9 Vorlesung "Intelligente Systeme" 50 2. Ein Beispiel Auffinden der Schwelle mittels Histogramm-Auswertung (9) Vorgehen nach obiger Methode: 6. Berechnung von A, B und C: A Z2 N2 ; B 2( Z N2 N Z2 ); C Z2 N2 N2 Z2 2 Z2 N2 ln 11 11 18 18 , PN 11 18 29 11 18 29 4 2 2 A 100 2 100 2 9 3 9 2 2 76 B 2 500 100 2 800 100 2 100 2 9 3 9 PZ N PZ Z PN Z 500 Z 2 12 (100) 2 11 N 800 2 9 N 2 (100) 2 11 2 100 2 2 2 2 2 29 C 25 100 2 100 2 64 100 2 100 2 100 4 ln 9 9 3 3 9 2 100 2 18 29 3 50 128 4 3 11 100 4 ln 9 3 3 9 9 18 Vorlesung "Intelligente Systeme" 51 2. Ein Beispiel Auffinden der Schwelle mittels Histogramm-Auswertung (10) Vorgehen nach obiger Methode: 7. Berechnung der Schwelle durch Lösung der quadratischen Gleichung ~ 2 ~ A MT B MT C 0 B B2 4 A C ~ MT 720 2 A Vorlesung "Intelligente Systeme" 52 2. Ein Beispiel Auffinden der Schwelle mittels Histogramm-Auswertung (11) Vorgehen nach obiger Methode: 8. Anwenden der Schwelle auf neues Datenmaterial Winkelgeschwindigkeit eines Zyklus InduktionsSensor Drehmoment Berechnung Periode T Bestimmung Merkmalsextraktion: M=820 Drehmomentmaxima ja Normal Vorlesung "Intelligente Systeme" M > 720 ? nein Zündaussetzer 53 2. Ein Beispiel Motordiagnose für Verbrennungskraftmaschinen Geberradfehler, Höhenschlag, Störungen Schütteln Zündauss. p3 Phase Einspritzauss. p1 m2 p2 Ventilundicht.Auslauf Abbildung Beschreibungs(Zustands-)raum Motorfehler m1 p4 m3 Abbildung Zugänglicher Beobachtungs- oder Musterraum Meßraum Wechseldrehmoment- Drehzahlsensordaten muster Informationsgewinnung Vorlesung "Intelligente Systeme" 54 3. Statistische Fundamente Bayes´sche Entscheidungstheorie Wie treffe ich die optimale Entscheidung bei unvollständiger Information ? A-priori-Wahrscheinlichkeiten Ein betrachtetes System befindet sich in einem “wahren Zustand” c, z.B. c=c1 (normal) oder c=c2 (Zündaussetzer). Diese können sich zufällig abwechseln und treten mit den Wahrscheinlichkeiten P(c1) und P(c2) auf: A-priori-Wahrscheinlichkeiten. P(c1) + P(c2) =1, wenn keine weiteren Zustände. Fall 1: Keine weitere Information als P(c1) und P(c2) -> Entscheidungsregel über nächsten Zustand: c1, wenn P(c1) > P(c2) , sonst c2. Sinnvoll nur bei einer einzigen Entscheidung. Vorlesung "Intelligente Systeme" 55 3. Statistische Fundamente Bayes´sche Entscheidungstheorie Wie treffe ich die optimale Entscheidung bei unvollständiger Information ? Klassenbedingte Wahrscheinlichkeitsdichtefunktion p(x|c) Information x über das System (z.B. das Drehmoment M4) mit verschiedenen Ausprägungen in verschiedenen Zuständen (Klassen) c. Klassenbedingte Wahrscheinlichkeitsdichtefunktion p(x|c). p(x|c) c1 c2 Wahrscheinlichkeitsdichte für das Vorliegen eines Wertes des Merkmals x, wenn das System in Zustand c ist. Die Fläche unter der Kurve ist jeweils 1. x Fall 2: Wir verfügen über weitere Information x. Graphik aus Duda, Hart, Stork: Pattern Classification 2nd edition, Wiley-Interscience Vorlesung "Intelligente Systeme" 56 3. Statistische Fundamente Bayes´sche Entscheidungstheorie Wie treffe ich die optimale Entscheidung bei unvollständiger Information ? Fall 2: Wir verfügen über weitere Information x, also die Wahrscheinlichkeitsdichtefunktionen p(x|ci) für die verschiedenen Klassen und den aktuellen Wert von Merkmal x unseres Systems sowie die A-priori-Wahrscheinlichkeiten der Klassen P(ci). Dann ist die verknüpfte Wahrscheinlichkeitsdichte, dass das System in Zustand ci ist und dabei den Merkmalswert x hat: p(ci,x) = P(ci|x)p(x) = p(x|ci)P(ci). Wahrscheinlichkeit für Klasse ci Wahrscheinlichkeit für Klasse ci unter der Bedingung, dass ein Wert x vorliegt Wahrscheinlichkeitsdichte von Merkmal x, unter der Bed., dass Klasse ci vorliegt Wahrscheinlichkeitsdichte von Merkmal x Von Interesse P(ci|x). Mittels Bayes´scher Formel P(ci | x) p( x | ci ) P(ci ) mit p( x) p( x | ci ) P(ci ) p( x) i Vorlesung "Intelligente Systeme" 57 3. Statistische Fundamente Bayes´sche Entscheidungstheorie A posteriori Wahrscheinlichkeit, dass Klasse ci vorliegt, wenn das Merkmal die Ausprägung x hat: Likelihood Posterior P(ci | x) Prior p( x | ci ) P(ci ) mit p( x) p( x | ci ) P(ci ) p( x) i Evidence P(c|x) p(x|c) p( x | c1 ) P(c1 ) P(c1 | x) p( x | c1 ) P(c1 ) p( x | c2 ) P(c2 ) c1 c2 c2 P(c1) = 1/3 P(c2) = 2/3 P ( c2 | x ) p ( x | c2 ) P ( c2 ) p ( x | c1 ) P(c1 ) p( x | c2 ) P(c2 ) c1 x x Graphik aus Duda, Hart, Stork: Pattern Classification 2nd edition, Wiley-Interscience Vorlesung "Intelligente Systeme" 58 3. Statistische Fundamente Bayes´sche Entscheidungstheorie Wie treffe ich die optimale Entscheidung bei unvollständiger Information ? Fall 2: Entscheide c1 wenn P(c1|x) > P(c2|x), sonst c2. P(c|x) P(c1|x=14)=0.92 c2 c1 P(c1|x=14)=0.08 c1 c2 c1 c2 Vorlesung "Intelligente Systeme" x 59 3. Statistische Fundamente Mehr als ein Merkmal Numerische Merkmale und Merkmalsvektor Wechseldrehm. Betrachte Signale des Motordiagnosesystems. Einfachste Wahl der Merkmale: Äquidistante Abtastung der Amplitudendaten der Wechseldrehmomentkurve. M2 M3 M4 M5 M1 0 2 Kurbelwinkel Jedes Wechseldrehmomentmuster ist charakterisiert durch eine Menge von Drehmomentwerten. Die Menge der Drehmomentwerte kann als Spaltenvektor geschrieben werden: [M1, M2, M3, M4, M5]T. Vorlesung "Intelligente Systeme" 60 3. Statistische Fundamente Merkmale Mehr als ein Merkmal Wechseldrehm. Numerische Merkmale und Merkmalsvektor M2 M 3 M4 M5 M1 0 2 Kurbelwinkel Ein Drehmomentmuster wir dann repräsentiert durch den Vektor M = [M1, M2, M3, M4, M5] T im fünf-dimensionalen “Drehmomentwerteraum”. Ein Drehmomentwert heisst dann “Merkmal”, der Raum “Merkmalsraum“, der Vektor “Merkmalsvektor“. Merkmalsvektoren von verschiedenen Motorzuständen sollten getrennte Volumina im Merkmalsraum einnehmen. Vorlesung "Intelligente Systeme" 61 3. Statistische Fundamente Merkmalsraum Mehr als ein Merkmal Bild von Objekten unterschiedlicher Größe und Farbe Meßraum: Farbwerte der Pixel eines Kamerasensors Farbwert h Merkmalsauswahl: Merkmalsvariable Farbwert (h) und maximale Abmessung (l) xx xxx x x hi Merkmalsraum + ++ ++ + * + fi li Jeder Merkmalsvektor fi= [hi, li]T repräsentiert ein Muster. Wegen der statistischen Prozesse bei der Musterentstehung und beim Meßprozess werden Merkmale als “random variables” und Merkmalsvektoren als “random vectors” betrachtet. Maximale Abmessung l Vorlesung "Intelligente Systeme" 62 3. Statistische Fundamente Merkmalsraum Mehr als ein Merkmal p x | cj Wahrscheinlichkeitsdichtefunktion Wahrsch. Stichprobe Merkmal x2 x x x x x x x x x xx x x xx xx x xx x x x x xx x xx x x x x x x x Merkmalsve ktor xi 1i x x2i x x Merkmal x1 x x x px , px | c j x1 , x2 ,, xN Vorlesung "Intelligente Systeme" 63 3. Statistische Fundamente Merkmalsraum Mehr als ein Merkmal: Korrelation und Kovarianz Wahrscheinlichkeitsdichtefunktion p x | c j Zwei unterschiedliche stochastische Größen (z.B. Merkmale) x1 und x2 Maßzahl für montonen Zusammenhang zwischen x1 und x2 : K(x1 , x2 ) K( x1 , x2 ) 0 wenn gleichsinniger Zusammenhang zw. x1 und x2 K( x1 , x2 ) 0 wenn gegensinniger Zusammenhang zw. x1 und x2 K( x1 , x2 ) 0 wenn kein Zusammenhang zw. x1 und x2 K(x1 , x2 ) Ex1 E( x1 )x2 E( x2 ) Die Größe von K hängt von den Maßeinheiten von x1 und x2 ab. Daher Invarianz durch Normierung mit Standardabweichung: Korrelation C K( x1 , x2 ) 2 C( x1 , x2 ) mit ( x) E x E ( x) ( x1 ) ( x2 ) Vorlesung "Intelligente Systeme" 64 3. Statistische Fundamente Merkmalsraum Mehr als ein Merkmal, mehrere Klassen Graphik aus Duda, Hart, Stork: Pattern Classification 2nd edition, Wiley-Interscience Vorlesung "Intelligente Systeme" 65 3. Statistische Fundamente Merkmalsraum Mehr als ein Merkmal, mehrere Klassen P (c j | x ) P(c4 | x) P(c1 | xT ) Endliche Menge von Klassen {c1,c2,…,cC} mit zugehörigen Wahrscheinlichkeitsdichten P(c3 | x ) p( x | c j ) Bayes Formel für a posteriori Wahrscheinlichkeit P(c2 | x) p ( x | c j ) P(c j ) P(c j | x ) mit p( x ) C p ( x ) p ( x | c j ) P (c j ) j 1 xT Entscheidungsregel: Entscheide ci , wenn j i : P(ci | x ) P(c j | x ) Vorlesung "Intelligente Systeme" 66 3. Statistische Fundamente Merkmalsraum Entscheidungsflächen und -funktionen Entscheidungsregel: Entscheide ci , wenn j i : P(ci | x ) P(c j | x ) Teilt Merkmalsraum in Regionen Ri , innerhalb derer P(ci | x ) P(c j | x ) j i R3 R4 xT R2 R1 Entscheidungsflächen sind Grenzflächen zwischen den Regionen xT R1 P(c1 | xT ) P(c j | xT ) j 1 Vorlesung "Intelligente Systeme" 67 3. Statistische Fundamente Merkmalsraum Entscheidungsflächen und -funktionen Entscheidungsregel: Entscheide ci , wenn j i : P(ci | x ) P(c j | x ) Entscheidungsregel gilt auch für monotone Funktionen g (Entscheidungsfunktionen) von P: Entscheide ci , wenn j i : g i ( x ) g j ( x ) p( x | ci ) P(ci ) g i ( x ) P(ci | x ) C , p ( x | c j ) P (c j ) j 1 alternativ : g i ( x ) p( x | ci ) P(ci ), (konst. Nenner weglassen) alternativ : g i ( x ) ln p( x | ci ) ln P(ci ) (logarithmieren) Vorlesung "Intelligente Systeme" 68 3. Statistische Fundamente Merkmalsraum Entscheidungsflächen und -funktionen Bei zwei Kategorien (Klassen) Entscheidungsregel Entscheide c1 , wenn g1 ( x ) g 2 ( x ) und entscheide c2 , wenn g1 ( x ) g 2 ( x ). Kann vereinfacht werden zu einer einzigen Entscheidungsfunktion g( x) g1 ( x) g2 ( x) deren Vorzeichen über die Klassenzugehörigkeit entscheidet: Entscheide c1 , wenn g ( x ) 0 und entscheide c2 , wenn g ( x ) 0. Bequeme Wahl von g: g ( x ) P(c1 | x ) P(c2 | x ), alternativ mit gi ( x ) ln p( x | ci ) ln P(ci ) p( x | c ) P(c1 ) g ( x ) ln 1 ln p ( x | c2 ) P ( c2 ) Vorlesung "Intelligente Systeme" 69 3. Statistische Fundamente Merkmalsraum Entscheidungsflächen und -funktionen Modellfunktion für klassenbedingte Wahrscheinlichkeitsdichte: Normalverteilung Bisher ein-dimensional: 1 p ( x) e 2 ( x )2 x p( x)dx, ( x ) 2 p( x)dx 2 2 2 Jetzt mehr-dimensional: 1 ( x )T S 1 ( x ) 1 p( x ) e 2 1 / 2 (2 ) d / 2 S x p( x )dx , Wahrsch. n xn p( xn )dxn , S ( x )( x )T p( x )dx kl (x k k )( xl l ) p( xk ) p( xl )dxk dxl Vorlesung "Intelligente Systeme" 70 3. Statistische Fundamente Merkmalsraum Entscheidungsflächen und -funktionen Normalverteilung Jetzt mehr-dimensional: p( x ) 1 (2 ) d /2 1/ 2 e S Wahrsch. 1 ( x )T S 1 ( x ) 2 x p( x )dx , n xn p( xn )dxn , S ( x )( x )T p( x )dx kl (x k k )( xl l ) p( xk ) p( xl )dxk dxl : Schwerpunk t S : Kovarianz - Matrix : symmetrisc h, positiv semi - definit Flächen konstanten Abstands vom Schwerpunk t : Hyper - Ellipsoide T 1 r ( x ) S ( x ) Mahalanobi s - Distanz des Vektors x von 2 Vorlesung "Intelligente Systeme" 71 3. Statistische Fundamente Merkmalsraum Entscheidungsflächen und -funktionen Beispiel: Annahme einer mehr-dimensionalen Normalverteilung Berechnung Schwerpunkt und Kovarianzmatrix aus Stichprobe Stichprobe x1i X x1 , x2 ,..., xN , xi x2i R 3 x3i x p( x )dx emp Schwerpunkt der Verteilung 1 N N x1i 1emp iN1 N 1 1 2emp xi x2i N i 1 N i 1 3emp 1 N x3i N i 1 Empirischer Schwerpunkt der Stichprobe Vorlesung "Intelligente Systeme" 72 3. Statistische Fundamente Merkmalsraum Entscheidungsflächen und -funktionen Beispiel: Annahme einer mehr-dimensionalen Normalverteilung Berechnung empirischer Schwerpunkt und empirische Kovarianzmatrix aus Stichprobe 1 N T S ( x )( x ) p( x )dx S emp ( xi emp )( xi emp )T N i 1 Im Fall drei-dimensionaler Vektoren: N ( x1i 1emp ) 2 N i 1 1 ( x1i 1emp )( x2i 2emp ) N i 1 N ( x1i 1emp )( x3i 3emp ) i 1 1emp )( x3i 3emp ) i 1 i 1 N N 2 ( x2i 2emp ) ( x2i 2emp )( x3i 3emp ) i 1 i 1 N N 2 ( x2i 2emp )( x3i 3emp ) ( x3i 3emp ) i 1 i 1 N ( x1i 1emp )( x2i 2emp ) p ( x Geschätzte Normalverteilung: Schätz ) N (x 1i 1 ( x emp )T S emp 1 ( x emp ) 1 e2 1 / 2 (2 ) d / 2 Semp Vorlesung "Intelligente Systeme" 73 3. Statistische Fundamente Merkmalsraum Entscheidungsflächen und -funktionen Bei Normalverteilung wegen e-Funktion Wahl von ln-Entscheidungsfunktion: gi ( x ) ln p( x | ci ) ln P(ci ) pi ( x ) 1 1 ( x i )T S i 1 ( x i ) 2 1/ 2 e (2 ) Si 1 T 1 d 1 g i ( x ) ( x i ) S i ( x i ) ln 2 ln S i ln P(ci ) 2 2 2 d /2 2 Einfachster Fall: Alle Merkmale unabhängig und mit gleicher Varianz Si I 1 d 1 T T d g i ( x ) 2 ( x i )T ( x i ) ln 2 ln P(ci ) 2 ( x T x 2i x i i ) ln P(ci ) ln 2 2 2 2 2 1 T 1 T 1 d 1 T 2 i x 2 i i 2 x T x ln 2 ln P(ci ) 2 i x const i , da x T x unabh. von i 2 2 2 Lineare Form g i ( x ) wiT x wi 0 Lineare Entscheidungsfunktion: Entscheidungsfläche Hyperebene gi ( x) g j ( x) 0 (wiT wTj ) x (wi 0 w j 0 ) 0 mit Normalenve ktor n i j Vorlesung "Intelligente Systeme" 74 3. Statistische Fundamente Merkmalsraum Entscheidungsflächen und -funktionen Normalverteilung 2 Einfachster Fall: Alle Merkmale unabhängig und mit gleicher Varianz Si I Lineare Entscheidungsfunktion: Entscheidungsfläche Hyperebene 1 T 1 T 1 d g i ( x ) 2 i x 2 i i 2 x T x ln 2 ln P(ci ) 2 2 2 1 T 1 T 1 T T g i ( x ) g j ( x ) 2 i 2 j x 2 i i j j ln P(ci ) ln P(c j ) 2 gi ( x) g j ( x) 0 (wiT wTj ) x (wi 0 w j 0 ) 0 mit Normalenve ktor n i j Weitere Einschränkung: A priori Wahrscheinlichkeiten P für alle Klassen gleich: 1 1 i T j T x i T i j T j 0 x i j 2 2 Entscheidungsregel: Ordne Vektor x der Klasse zu, zu deren Schwerpunkt vektor i er den kleinsten euklidischen Abstand ( x i ) 2 hat: Minimum-Distance Klassifikator Vorlesung "Intelligente Systeme" 75 3. Statistische Fundamente Merkmalsraum Entscheidungsflächen und -funktionen 2 Normalverteilung, 2 Kategorien Si I Entscheidungsfunktionen: Lineare Entscheidungsfunktion: Entscheidungsfläche Hyperebene g1 ( x ) g 2 ( x ) 0 ( w1T w2T ) x ( w10 w20 ) 0 mit Normalenve ktor n 1 2 ein-dim. Merkm.-Raum zwei-dim. Merkm.-Raum drei-dim. Merkm.-Raum Graphik aus Duda, Hart, Stork: Pattern Classification 2nd edition, Wiley-Interscience Vorlesung "Intelligente Systeme" 76 3. Statistische Fundamente Merkmalsraum Entscheidungsflächen und -funktionen Normalverteilung, 2 Kategorien Entscheidungsfunktionen: Entscheidungsfunktion p ( x | c1 ) P(c1 ) g ( x ) ln ln p ( x | c2 ) P ( c2 ) 1 T 1 ln p( x | ci ) ( x i ) S i ( x i ) 2 d 1 ln 2 ln S i 2 2 Entscheidungsflächen: Hyperquadriken 1 T 1 1 T 1 1 1 ( x 1 ) S1 ( x 1 ) ( x 2 ) S 2 ( x 2 ) ln S1 ln S 2 ln P(c1 ) ln P(c2 ) 0 2 2 2 2 Graphik aus Duda, Hart, Stork: Pattern Classification 2nd edition, Wiley-Interscience Vorlesung "Intelligente Systeme" 77 3. Statistische Fundamente Merkmalsraum Entscheidungsflächen und -funktionen Normalverteilung, 2 Kategorien Entscheidungsflächen: Hyperquadriken 1 T 1 1 T 1 1 1 ( x 1 ) S1 ( x 1 ) ( x 2 ) S 2 ( x 2 ) ln S1 ln S 2 ln P(c1 ) ln P(c2 ) 0 2 2 2 2 Ebenen Graphik aus Duda, Hart, Stork: Pattern Classification 2nd edition, Wiley-Interscience Vorlesung "Intelligente Systeme" 78 3. Statistische Fundamente Merkmalsraum Entscheidungsflächen und -funktionen Normalverteilung, 2 Kategorien Entscheidungsflächen: Hyperquadriken 1 T 1 1 T 1 1 1 ( x 1 ) S1 ( x 1 ) ( x 2 ) S 2 ( x 2 ) ln S1 ln S 2 ln P(c1 ) ln P(c2 ) 0 2 2 2 2 Paraboloide Ellipsoide Graphik aus Duda, Hart, Stork: Pattern Classification 2nd edition, Wiley-Interscience Vorlesung "Intelligente Systeme" 79 3. Statistische Fundamente Merkmalsraum Entscheidungsflächen und -funktionen Normalverteilung, 2 Kategorien Entscheidungsflächen: Hyperquadriken 1 T 1 1 T 1 1 1 ( x 1 ) S1 ( x 1 ) ( x 2 ) S 2 ( x 2 ) ln S1 ln S 2 ln P(c1 ) ln P(c2 ) 0 2 2 2 2 Hyperboloide Kugeln Graphik aus Duda, Hart, Stork: Pattern Classification 2nd edition, Wiley-Interscience Vorlesung "Intelligente Systeme" 80 3. Statistische Fundamente Merkmalsraum Wie weiter? Voraussetzung bisher: A priori Wahrscheinlichkeiten P (ci ) und klassen-bedingte Wahrscheinlichkeitsdichten p( x | ci ) bekannt. Realität: Nur Stichproben gegeben. Ansätze: 1. Parametrische Techniken: Annahme bestimmter parametrisierter Wahrscheinlichkeitsdichtefunktionen und Schätzung der Parameterwerte anhand Stichprobe, Einsetzen in Bayes Framework. A) Maximum-Likelihood Schätzung B) Bayes Learning 2. Nicht-parametrische Techniken 3. Direkte Bestimmung der Parameter der Entscheidungsflächen anhand Stichprobe. Vorlesung "Intelligente Systeme" 81 3. Statistische Fundamente Merkmalsraum Wie weiter? Möglichkeit 1 bei gegebener Stichprobe: Schätzung der pdf und a-priori-Wahrsch. Aus Stichprobe: Bildung Histogramm, relative Häufigkeiten h(ci) Modellbildung: Annahme einer Modellfunktionenklasse für klassenbedingte Wahrscheinlichkeitsdichte, z.B. Gaussfunktion Schätzung der Parameter der Funktion -> Instanz der Funktionenklasse, die das Histogramm am besten approximiert (Schätzfunktion der klassenbedingten Wahrscheinlichkeitsdichte): pS ( x | ci ) Anwendung Bayes: Benutze pS ( x | ci ) als Näherung für p( x | ci ) und relative Häufigk. H(ci) für P(ci) und wende Bayes´sche Entscheidungsregel an: pS ( x | ci ) H (ci ) PS (ci | x) pS ( x) Entscheide ci , wenn j i : PS (ci | x ) PS (c j | x ) Vorlesung "Intelligente Systeme" 82 3. Statistische Fundamente Merkmalsraum Wie weiter? Möglichkeit 1 bei gegebener Stichprobe: Schätzung der pdf und a-priori-Wahrsch. j j Stichprobe c j : x1 , x2 ,, xN x x Wahrsch. Merkmal x2 x x p x Geschätzte pdf und apw S | c j , PS (c j ) x x x j x x xx x x xx xx x x x x xxxx xx xx x x x x x x x x x Merkmal x1 x x x Anwendung Bayes Entscheidungsregel: Entscheidungsfläche Vorlesung "Intelligente Systeme" 83 3. Statistische Fundamente Merkmalsraum Wie weiter? x x x x x x x x x xx x x xx xx x xx x x x x xx x xx x x x x x x x x x x x Merkmal x2 Möglichkeit 2 bei gegebener Stichprobe: Finde eine Entscheidungsfläche, welche die Stichprobenvektoren einer Klasse von denen der anderen Klassen trennt. Merkmal x1 x Vorlesung "Intelligente Systeme" 84 4. Entscheidungsflächen und -funktionen Statistische Klassifikationsaufgabe Aufgabe 1: Gegeben sei eine Stichprobe mit bekannten Klassenzugehörigkeiten (Klasse 1 und Klasse 2). Finde ein Trennmöglichkeit, um zu entscheiden, zu welcher Klasse ein unbekanntes Muster gehört. h Überwachte Methoden Merkmalsraum Klasse 1 xx x xx x x + ++ ++ + * + Trennlinie Klasse 2 l Vorlesung "Intelligente Systeme" 85 4. Entscheidungsflächen und -funktionen Klassifikationsaufgabe Aufgabe 2: Unter der Annahme, daß es sich um zwei Klassen handelt, finde die zugehörigen Cluster in der Stichprobe mit den Mustern. Z.B. Learning Vector Quantisation (LVQ), Self Organising Maps (SOMs). h Unüberwachte Methoden Merkmalsraum Klasse 1 xx x xx x x + ++ ++ + * + Klasse 2 l Vorlesung "Intelligente Systeme" 86 4. Entscheidungsflächen und -funktionen h Überwachte Methoden Lineare Klassifikatoren Einschichtiges Perceptron Kleinste Quadrate Klass. Lineare Support Vektor Maschine Klasse 1 xx xxx x x + ++ ++ + * + Gerade Trennlinie Klasse 2 Nichtlineare Klassifikatoren Mehrschicht-Perceptron logistisch polynom radiale Basisfunktionen Support-Vektor-Maschinen h l Klasse 1 Trennkurve x x xx x x x x x xx x x + + ++ x x x ++ +++ + x x + + + ++ xx x + + + Klasse 2 + + ++ + + + l Vorlesung "Intelligente Systeme" 87 5. Lineare Klassifikatoren Grundlagen Das Perzeptron Nicht-lineare Klassen und Mehrklassen-Ansatz Kleinste Quadrate lineare Klassifikatoren Stochastische Approximation und der LMS Algorithmus Schätzung mittels Quadratfehlersumme Mehrklassen-Verallgemeinerung Lineare Support Vektor Maschine Vorlesung "Intelligente Systeme" 88 5. Lineare Klassifikatoren Grundlagen Vorlesung "Intelligente Systeme" 89 5. Lineare Klassifikatoren Der Merkmalsraum wird durch Hyperebenen aufgeteilt. Vorteil: Einfachheit und geringer Berechnungsaufwand. Nachteile: Die zugrundeliegenden statistischen Verteilungen der Trainingsmuster werden nicht vollständig genutzt. Nur linear separierbare Klassen werden korrekt klassifiziert. Entscheidungs-Hyperebene: Eine Entscheidungs-Hyperebene teilt den Merkmalsraum in zwei Halbräume: Punkte (Vektoren) von Halbraum 1 Klasse 1 Punkte von Halbraum 2 Klasse 2. Hyperebene im N-dimensionalen Merkmalsraum beschrieben durch Normalenvektor n = [n1, n2,..., nN]T und senkrechten Abstand d zum Ursprung. Ist x ein Merkmalsvektor, z der Abstand des Punktes x von der Hyperebene und d der Abstand der Hyperebene zum Ursprung, dann ist die Entscheidungs-Hyperebene definiert durch den Gewichtsvektor w = [w1, w2,..., wN]T und w0, bezeichnet als Schwellwert: g(x) = wT x + w0 =! 0 wobei w und w0 so gewählt werden, dass Merkmalsvektoren x verschiedener Klassen ein unterschiedliches Vorzeichen von g(x) ergeben. Vorlesung "Intelligente Systeme" 90 5. Lineare Klassifikatoren Zweidimensionaler Fall: Geometrie der Entscheidungs-Linie (-Hyperebene) x2 Merkmalsraum w1 w w2 d w0 w w 2 1 2 2 d z z x g( x ) w12 w22 x1 Entscheidungshyperebene wT x w0 0 T g x w x w0 Entscheidungsfunktion Das Vorzeichen von g(x) gibt die Klassenzugehörigkeit an. Wie werden die unbekannten Gewichtswerte w1, w2,..., wN und w0 berechnet? Vorlesung "Intelligente Systeme" 91 Lineare Klassifikatoren Das Perzeptron Die Perzeptron-Kostenfunktion Der Perzeptron Algorithmus Bemerkungen zum Perzeptron Algorithmus Eine Variation des Perzeptron-Lernschemas Arbeitsweise des Perzeptrons Vorlesung "Intelligente Systeme" 92 5. Lineare Klassifikatoren Der Perzeptron Algorithmus Annahme: Es liegen zwei Klassen c1 and c2 vor, die linear separierbar sind. Es existiert eine Entscheidungs-Hyperebene w x + w0= 0 derart, daß wT x w0 0 x c1 wT x w0 0 x c2 Umformulierung mit erweiterten N+1-dimensionalen Vektoren: x´ x, 1]T und w´ w, w0]T ergibt wT x 0 x c1 wT x 0 x c2 Die Aufgabe wird als Minimierungsproblem der Perzeptron-Kostenfunktion formuliert. Vorlesung "Intelligente Systeme" 93 5. Lineare Klassifikatoren Die Perzeptron-Kostenfunktion Y sei diejenige Untermenge der Trainingsvektoren, welche durch die Hyperebene (definiert durch Gewichtsvektor w) fehlklassifiziert werden. Die Variable dx wird so gewählt, daß dx = -1 wenn x e c1 und dx = +1 wenn x e c2. T J w d x w x xY J ist dann stets positiv und wird dann Null, wenn Y eine leere Menge ist, d.h., wenn es keine Fehlklassifikation gibt. J ist stetig und stückweise linear. Nur wenn sich die Anzahl der fehlklassifizierten Vektoren ändert, gibt es eine Diskontituität. Für die Minimierung von J wird ein iteratives Schema ähnlich der Gradientenabstiegsmethode verwendet. Vorlesung "Intelligente Systeme" 94 Kostenfunktion (Anzahl Fehler) Vorlesung "Intelligente Systeme" 95 Kostenfunktion (Perzeptron) Vorlesung "Intelligente Systeme" 96 Kostenfunktion (quadratisch) Vorlesung "Intelligente Systeme" 97 5. Lineare Klassifikatoren Gradientenmethode für die Perzeptron-Kostenfunktion J (w) w2 w1 Graphik aus Duda, Hart, Stork: Pattern Classification 2nd edition, Wiley-Interscience Vorlesung "Intelligente Systeme" 98 5. Lineare Klassifikatoren Der Perzeptron-Algorithmus Iterative Anpassung des Gewichtsvektors entlang dem Gradienten der Kostenfunktion: J ( w) w( k 1) w( k ) k w w w ( k ) (1) k: Iterationsindex, k: Lernrate (positiv) (1) ist nicht definiert an Unstetigkeitsstellen von J. An allen Unstetigkeitsstellen von J gilt: J ( w) T dxw x dxx w xY J w xY (2) Substitution der rechten Seite von (2) in (1) ergibt: w( k 1) w( k ) k dx x x Y wodurch der Perzeptron-Algorithmus an allen Punkten definiert ist. Vorlesung "Intelligente Systeme" 99 5. Lineare Klassifikatoren Geometrische Interpretation für den 2d Merkmalsraum Trennlinie im Schritt k+1 x2 Letzter Schritt des Perzeptron-Algorithmus: Nur noch ein einziger Punkt x fehlklassifiziert. x Trennlinie im Schritt k w(k+1) x1 w(k) w wurde in die Richtung von x gedreht. bestimmt die Stärke der Drehung. Vorlesung "Intelligente Systeme" 100 5. Lineare Klassifikatoren Bemerkungen zum Perzeptron-Algorithmus 1. Der Perzeptron-Algorithmus konvergiert zu einer Lösung in einer endlichen Anzahl von Schritten, vorausgesetzt, daß die Folge k richtig gewählt wird. Es kann gezeigt werden, dass dies der Fall ist, wenn gilt: t lim t t 2 und lim k k k 1 t k 1 Ein Beispiel einer Folge, welche obige Bedingung erfüllt, ist k = c/k, da t 1 lim r divergent für r <= 1, aber konvergent für r >1. t k 1 k 2. Die Konvergenzgeschwindigkeit hängt von der Folge kab. 3. Die Lösung ist nicht eindeutig, da es immer eine Schar von Hyperebenen gibt, welche zwei linear separierbare Klassen trennt. Vorlesung "Intelligente Systeme" 101 5. Lineare Klassifikatoren Eine Variation des Perzepton Lernschemas Bisher: Gesamte Trainingsvektormenge in einem Trainingsschritt. Neu: Ein einziger Trainingsvektor in einem Trainingsschritt und Wiederholung für alle Vektoren der Trainingsmenge: “Trainingsepoche”. Die Trainingsepochen weden wiederholt, bis Konvergenz erreicht ist, d.h., wenn alle Trainingsvektoren korrekt klassifiziert werden. Wiederhole, bis Konvergenz erreicht ist { Wiederhole für alle Trainingsvektoren { w(k 1) w(k ) x( k ) w(k 1) w(k ) x( k ) w(k 1) w(k ) wenn wenn T x( k ) c1 und w (k ) x( k ) 0 x( k ) c2 und wT (k ) x( k ) 0 sonst } } Dieses Schema ist Mitglied der “Belohnungs- und Bestrafungs-”Schemata. Es konvergiert ebenso in einer endlichen Anzahl von Iterationen. Vorlesung "Intelligente Systeme" 102 Perzeptronalgorithmus Vorlesung "Intelligente Systeme" 103 Perzeptronalgorithmus Vorlesung "Intelligente Systeme" 104 Perzeptronalgorithmus Vorlesung "Intelligente Systeme" 105 Perzeptronalgorithmus Vorlesung "Intelligente Systeme" 106 5. Lineare Klassifikatoren Das Perzeptron im Betrieb Gewichtsvektor w und Schwellwert w0 wurden vom Lernalgorithmus gefunden. Die Klassifikationsprozedur lautet dann: Wenn Wenn T w x w0 0 ordne zu : x zu c1 wT x w0 0 ordne zu : x zu c2 Dies kann als Netzwerk interpretiert werden: x1o x2o . . . xNo w1 w2 . wN S w0 f Die Elemente des Merkmalsvektors werden auf die Eingangsknoten gegeben. Jedes wird multipliziert mit den entsprechenden Gewichten der Synapsen. Die Produkte werden zusammen mit dem Schwellwert aufsummiert. Das Ergebnis wird von einer Aktivierungsfunktion f verarbeitet (z.B. +1 wenn Ergebnis > 0, -1 sonst). Dieses grundlegende Netzwerk wird als Perzeptron oder Neuron bezeichnet. Vorlesung "Intelligente Systeme" 107 5. Lineare Klassifikatoren Perzeptron-Lernphase: Bestimmung des erweiterten Gewichtsvektors Wiederhole, bis Konvergenz erreicht ist { Wiederhole für alle Trainingsvektoren { w(k 1) w(k ) x( k ) w(k 1) w(k ) x( k ) w(k 1) w(k ) wenn wenn x( k ) c1 und wT (k ) x( k ) 0 x( k ) c2 und wT (k ) x( k ) 0 sonst } x1o } x2o Perzeptron-Betriebsphase: Klassifikation eines (erweiterten) Merkmalsvektors. . 1 wenn x c t 1 . y sign wT conv xt xNo 0 wenn x c t 2 Vorlesung "Intelligente Systeme" w1 w2 . wN S f w0 108 5. Lineare Klassifikatoren Übung zu Perzeptrons: Programmiere und benutze beide Perzeptron-Algorithmen. Starte mit w=(1,0), w0=2 und weiteren Trennlinien. Menge 1: Klasse 1: x1,1=[1,1]T, x1,2=[2,1]T, x1,3=[1,2]T, x1,4=[2,2]T, x1,5=[1,3]T Klasse 2: x2,1=[5,1]T, x2,2=[6,1]T, x2,3=[5,2]T, x2,4=[6,2]T, x2,5=[5,3]T Menge 2: Klasse 1: x1,1=[1,1]T, x1,2=[2,1]T, x1,3=[1,2]T, x1,4=[4,2]T, x1,5=[1,3]T Klasse 2: x2,1=[3,1]T, x2,2=[4,1]T, x2,3=[3,2]T, x2,4=[2,2]T, x2,5=[4,3]T Beobachte und beschreibe das Konvergenzverhalten. Vorlesung "Intelligente Systeme" 109 5. Lineare Klassifikatoren Nicht-lineare Klassen und Mehrklassen-Ansatz Lineare Klassifikation nicht linear separierbarer Klassen Lineare Separierung von mehr als zwei Klassen Vorlesung "Intelligente Systeme" 110 5. Lineare Klassifikatoren Lineare Klassifikation nicht linear separierbarer Klassen Klassen nicht linear separierbar: Perzeptron-Algorithmus konvergiert nicht. Erweiterung des Perzeptron-Lernalgorithmus nach Gallant: Pocket-Algorithmus. Konvergiert zu einer optimalen Lösung in dem Sinne, dass die Anzahl der Fehlklassifikationen minimal ist. Der Pocket-Algorithmus: Schritt k=0: • Initialisiere Gewichtsvektor w(0) mit Zufallszahlen. • Definiere einen Zufalls-Gewichtsvektor wp und speichere ihn (“in the pocket”). • Setze den Zähler hp von wp auf Null. Iteriere: • Schritt k+1 • Berechne w(k+1) aus w(k) mittels Perzeptron-Regel. • Benutze w(k+1), um die Anzahl h korrekt klassifizierter Trainingsvektoren zu messen. • Wenn h > hp, ersetze wp durch w(k+1) und den aktuellen Wert von hp durch h. Vorlesung "Intelligente Systeme" 111 5. Lineare Klassifikatoren Lineare Separierung von mehr als zwei Klassen M Klassen (hier M=4) c1 c1 Nicht c1 Nicht c4 c4 H12 c2 c4 H23 H24 c1 1. c3 Nicht c3 c3 c2 Mehrdeutiges Gebiet c1 H13 M lineare Klassifikatoren, die je eine Klasse von allen anderen unterscheiden oder c3 c1 2. c2 Mehrdeutiges Gebiet c3 H14 M(M-1)/2 Klassifikatoren, die jeweils ein paar von Klassen unterscheiden c2 c3 c2 c 4 c4 c3 c4 H34 Vorlesung "Intelligente Systeme" oder ... 112 5. Lineare Klassifikatoren Lineare Separierung von mehr als zwei Klassen ... Oder Kesler: M lineare Entscheidungsfunktionen gi(x) = wiT x + w0i mit Klassenzuordnung des Vektors x zu Klasse i, wenn w x T T wi x wj x j i mit w und x 1 w0 “Lineare Maschine” H15 H25 H12 R5 c 5 R1 c1 H13 R3 R1 R2 c2 c1 c3 H23 H14 H35 R2 R3 c 3 c2 H13 R4 H23 c4 H34 H24 Zuordnungsgrenzen der linearen Maschine für drei bzw. fünf Klassen Vorlesung "Intelligente Systeme" 113 5. Lineare Klassifikatoren Lineare Separierung von mehr als zwei Klassen Lineare Maschine: Verallgemeinerung des Perzeptrons auf M-Klassen-Aufgaben: • Eine lineare Unterscheidungsfunktion wi sei definiert für jede der Klassen ci i = 1,2,...,M. • Ein l+1 dimensionaler (inklusive w0) Merkmalsvektor x wird Klasse ci zugeordnet, wenn T T wi x w j x j i Vorlesung "Intelligente Systeme" 114 5. Lineare Klassifikatoren Lineare Separierung von mehr als zwei Klassen Lineare Maschine: Wirkung im Merkmalsraum T T wi x w j x j i Trennebenen zwischen Klassen ci und cj: T (wi w j ) x 0 R1 H12 c1 H13 R3 R2 c2 c3 H23 Vorlesung "Intelligente Systeme" 115 5. Lineare Klassifikatoren Lineare Separierung von mehr als zwei Klassen Lineare Maschine: T T wi x w j x, j i Annahme: Drei Klassen mit Gewichtsvektoren w1 , w2 , w3 Für einen Stichprobenvektor xc1der Klasse c1 gilt: T T T w1 xc1 w2 xc1 oder W X c1, 2 und w1 xc1 0 mit W w2 und X c1, 2 xc1 w3 0 Block-Gewichtsvektor Block-Merkmalsvektoren w1 xc1 T T T w1 xc1 w3 xc1 oder W X c1,3 0 mit W w2 und X c1,3 0 w3 xc1 Vorlesung "Intelligente Systeme" 116 5. Lineare Klassifikatoren T T T w1 xc1 w2 xc1 oder W X c1, 2 xc1 xc 2 und w1 xc1 0 mit W w2 und X c1, 2 xc1 w3 0 Block-Gewichtsvektor Block-Merkmalsvektoren w x 1 c1 T T T w1 xc1 w3 xc1 oder W X c1,3 0 mit W w2 und X c1,3 0 w3 xc1 w x 1 c2 T T w2 xc 2 w1 xc 2 oder W T X c 2,1 0 mit W w2 und X c 2,1 xc 2 w3 0 und Block-Gewichtsvektor Block-Merkmalsvektoren 0 w1 T T T w2 xc 2 w3 xc 2 oder W X c 2,3 0 mit W w2 und X c 2,3 xc 2 xc 2 w3 Vorlesung "Intelligente Systeme" 117 5. Lineare Klassifikatoren Lineare Separierung von mehr als zwei Klassen Kesler´s Konstruktion: Für jeden der Trainingsvektoren aus Klasse ci konstruiere M-1 Vektoren xij=[0,0,...,x,...,-x,...,0]T, j = 1,2,…M wobei j i Block-Vektoren der Dimension (l+1)Mx1 überall Nullen haben, M: Anzahl der Klassen außer an Blockposition i und j, wo sie x bzw. -x für j i haben. Konstruiere ferner einen Blockgewichtsvektor w = [w1, w2, ..., wM]T. Wenn x e ci dann impliziert dies: w xij 0 j 1, 2,..., M , j i Benutze den Perzeptron-Algorithmus, um eine Trennebene im (l+1)M dimensionalen Raum zu berechnen, so dass alle (M-1)N Trainingsvektoren auf der positiven Seite liegen. Das Verfahren konvergiert nur, wenn alle Klassen linear separierbar sind ! Vorlesung "Intelligente Systeme" 118 5. Lineare Klassifikatoren Beispiel für Kesler´s Konstruktion (Teil1) Dreiklassenproblem im 2d Merkmalsraum: c1 : [1,1]T, [2,2]T, [2,1]T c2 : [1,-1]T, [1,-2]T, [2,-2]T c3 : [-1,1]T, [-1,2]T, [-2,1]T linear separierbar Quadrant 1 Quadrant 4 Quadrant 2 Erweiterung auf 3 Dimensionen und Anwendung von Kesler´s Konstruktion: xij=[0,0,...,x,...,-x,...,0]T, j = 1,2,…M wobei j i Block-Vektoren der Dimension (l+1)Mx1überall Nullvektoren, außer an Blockposition i and j, wo x bzw. -x für j i c1: [1,1]T gibt x1,2 = [1,1,1,-1,-1,-1,0,0,0]T und x1,3 = [1,1,1,0,0,0,-1,-1,-1]T c2: [1,-2]T gibt x2 1 = [-1,2,-1,1,-2,1,0,0,0]T und x2,3 = [0,0,0,1,-2,1,-1,2,-1]T c3:[-2,1]T gibt x3 1 = [2,-1,-1,0,0,0,-2,1,1]T und x3 2 = [0,0,0,2,-1,-1,-2,1,1]T usw. um die anderen 12 Vektoren zu erhalten. Die Gewichtsvektoren für c1, c2 und c3 lauten: w1 = [w11, w12, w10]T, w2 = [w21, w22, w20]T, w3 = [w31, w32, w30]T Kesler: w = [w1, w2, w3]T Anwendung des Perzeptron-Algorithmus unter der Bedingung w x 0 Vorlesung "Intelligente Systeme" 119 5. Lineare Klassifikatoren Beispiel für Kesler´s Konstruktion (Teil2) Dreiklassenproblem im 2d Merkmalsraum: linear separierbar Klasse c1 : xa = [1,1]T, xb = [2,2]T, xc = [2,1]T Quadrant 1 Klasse c2 : xd = [1,-1]T, xe = [1,-2]T, xf = [2,-2]T Quadrant 4 g T h T i T Klasse c3 : x = [-1,1] , x = [-1,2] , x = [-2,1] Quadrant 2 Block-Merkmalsvektoren: c1: xa = [1,1]T gibt xa12 = [1,1,1,-1,-1,-1,0,0,0]T und xa1,3 = [1,1,1,0,0,0,-1,-1,-1]T xb =[2,2]T gibt xb12 = [2,2,1,-2,-2,-1,0,0,0]T und xb1,3 = [2,2,1,0,0,0,-2,-2,-1]T xc =[2,1]T gibt xc12 = [2,1,1,-2,-1,-1,0,0,0]T und xc1,3 = [2,1,1,0,0,0,-2,-1,-1]T c2: xd = [1,-1]T gibt xd21 = [-1,1,-1,1,-1,1,0,0,0]T und xd2,3 = [0,0,0,1,-1,1,-1,1,-1]T xe =[1,-2]T gibt xe21 = [-1,2,-1,1,-2,1,0,0,0]T und xe2,3 = [0,0,0,1,-2,1,-1,2,-1]T xf =[2,-2]T gibt xf21 = [-2,2,-1,2,-2,1,0,0,0]T und xf2,3 = [0,0,0,2,-2,1,-2,2,-1]T c3: xg = [-1,1]T gibt xg31 = [1,-1,-1,0,0,0,-1,1,1]T und xg3 2 = [0,0,0,1,-1,-1,-1,1,1]T xh =[-1,2]T gibt xh31 = [1,-2,-1,0,0,0,-1,2,1]T und xh3 2 = [0,0,0,1,-2,-1,-1,2,1]T xi =[-2,1]T gibt xi31 = [2,-1,-1,0,0,0,-2,1,1]T und xi3 2 = [0,0,0,2,-1,-1,-2,1,1]T Die Gewichtsvektoren für c1, c2 und c3 lauten: w1 = [w11, w12, w10]T, w2 = [w21, w22, w20]T, w3 = [w31, w32, w30]T Block-Gewichtsvektor w = [w1, w2, w3]T = [w11, w12, w10, w21, w22, w20,w31, w32, w30]T Anwendung des Perzeptron-Algorithmus unter der Bedingung Y {xim, j Y : wT xim, j 0} wT x 0 w(k 1) w(k ) k Vorlesung "Intelligente Systeme" m x i, j xim, j Y 120 5. Lineare Klassifikatoren Beispiel für Kesler´s Konstruktion (Teil3) Dreiklassenproblem im 2d Merkmalsraum: Klasse c1 : xa = [1,1]T, xb = [2,2]T, xc = [2,1]T Klasse c2 : xd = [1,-1]T, xe = [1,-2]T, xf = [2,-2]T Klasse c3 : xg = [-1,1]T, xh = [-1,2]T, xi = [-2,1]T linear separierbar Quadrant 1 Quadrant 4 Quadrant 2 Ergebnis Perzeptron-Algorithmus: w=[5.13, 3.60, 1.00, -0.05, -3.16, -0.4, -3.84, 1.28, 0.69 ]T w1 = [5.13, 3.60, 1.00]T, w2 = [-0.05, -3.16, -0.4]T, w3 = [-3.84, 1.28, 0.69 ]T Bestimmung Klassenzugehörigkeit neuer Vektor: xp = [1.5, 1.5]T x’p = [1.5, 1.5, 1]T Berechnung x’pw1 = 14.095, x’pw2 = -5.065, x’pw3 = -3.3 ergibt x’pw1 > x’pw3 > x’pw2 daraus folgt xp Element der Klasse c1 Vorlesung "Intelligente Systeme" 121 Lineare Klassifikatoren Kleinste-Quadrate lineare Klassifikatoren Vorlesung "Intelligente Systeme" 122 Lineare Klassifikatoren Kleinste-Quadrate Lineare Klassifikatoren Wegen der Einfachheit linearer Klassifikatoren ist ihr Einsatz bisweilen auch dann wünschenswert, wenn die Klassifikationsaufgabe nicht-linear ist. Anstelle des Pocket-Algorithmus können Kleinste-Quadrate-Methoden verwendet werden, um eine optimale Lösung zu finden. Gegeben: linearer Klassifikator w und Stichproben-Merkmalsvektor x (jeweils erweiterte Vektoren). Ausgang des Klassifikators yist wT x x T w Der gewünschte Ausgang ist ysoll ( x ) y 1 (2-Klassen-Problem) Methode der kleinsten Quadrate: Optimaler Gewichtsvektor w durch Minimierung des mittleren quadratischen Fehlers (MSE: mean square error) J zwischen tatsächlichem und gewünschtem Ausgang: 2 J ( w) E y x T w , wˆ arg min J ( w ) w E[...] bezeichnet den Erwartungwert über die Verteilung: E f x Minimierung der obigen Gleichung bezüglich w bedeutet: J ( w) T ! T 2 E x ( y x w) 0 für w wˆ E xy E x ( x wˆ ) w 1 E[ xy] E[ xx T ]wˆ wˆ E[ xx T ] E[ xy] f x p( x )dx , Vorlesung "Intelligente Systeme" 123 Lineare Klassifikatoren Die obige Gleichung wird also gelöst durch: ˆ w Rx1E[ xy] Wobei R die Korrelationsmatrix der l-dimensionalen Vektoren x ist: E[ x1 x1 ] E[ x1 x2 ] E[ x1 xl ] T E[ x2 x1 ] Rx E[ xx ] E [ x x ] E [ x x ] l 1 l l E[xy] ist die Kreuzkorrelation zwischen tatsächlichem und gewünschtem Ausgang: x1 y E[ xy ] E[ ] xl y Wenn R invertierbar ist, resultiert der optimale Gewichtsvektor aus der Lösung eines linearen Gleichungssystems. Vorlesung "Intelligente Systeme" 124 Lineare Klassifikatoren Zusammenfassung der “Mean Square Error Estimation” (MSE): Lösung gegeben durch folgende Gleichungen: ˆ w Rx1E[ xy] E[ x1 x1 ] E[ x1 x2 ] E[ x1 xl ] T E[ x2 x1 ] Rx E[ xx ] E [ x x ] E [ x x ] l 1 l l x1 y E[ xy ] E[ ] xl y R ist die Korrelationsmatrix der Verteilung der Merkmalsvektoren. Aber leider (wie bei Bayes): Eine Lösung der obigen Gleichungen benötigt die Kenntnis der Verteilungsfunktion. Diese ist im Allgemeinen nicht bekannt, sondern nur Stichprobe gegeben. Daher: Approximation muss gefunden werden, welche die verfügbaren StichprobenMerkmalsvektoren benutzt: Der LMS-Algorithmus Vorlesung "Intelligente Systeme" 125 Lineare Klassifikatoren Stochastische Approximation und der LMS Algorithmus Vorlesung "Intelligente Systeme" 126 Lineare Klassifikatoren Stochastische Approximation und der LMS Algorithmus Wir betrachten eine Gleichung der Form EF ( xk , w) 0 xk , k 1, 2, ... wobei wie z.B. T 2E x ( y x w) 0 eine Folge von “random vectors” der unbekannten Verteilung ist, F(.,.) ist eine Funktion und w der Vektor der unbekannten Gewichtswerte. Dann kann eine Lösung gefunden werden durch Anwendung des folgenden iterativen Schemas (Robbins und Monroe 1951): ˆ (k ) w ˆ (k 1) r F ( x , w ˆ (k 1)) w k k Wenn r k 1 Dann k und r 2 k was impliziert k 1 lim prob wˆ (k ) w 1 and k lim r k 0 k ˆ 2 lim E w(k ) w 0 k was bedeutet, daß die gewünschte Konvergenz erreicht wurde. Vorlesung "Intelligente Systeme" 127 Lineare Klassifikatoren Mithilfe dieser Erkenntnis kann die ursprüngliche Gleichung ohne genaue Kenntnis der Verteilung gelöst werden. Allerdings wird eine hinreichend große Stichprobe von Merkmalsvektoren benötigt. EF ( xk , w) 0 ˆ ˆ ˆ w (k ) w (k 1) rk F ( xk , w (k 1)) T 2 ˆ J ( w) E y x w , w arg min J ( w ) w J ( w) T 2 E x ( y x w) 0 w Dann wird substituiert durch für w wˆ , ˆ T ˆ F ( xk , w (k 1)) xk ( yk xk w (k 1)) wobei {xk} die Menge der Trainings-Merkmalsvektoren und {yk} die Menge der entsprechenden gewünschten Ausgangswerte +-1 darstellt. ˆ ˆ T ˆ w (k ) w (k 1) rk xk ( yk xk w (k 1)) Dieses iterative Schema wird als Widrow-Hoff Algorithmus bezeichnet. Er konvergiert asymptotisch gegen die MSE-Lösung. Vorlesung "Intelligente Systeme" 128 Lineare Klassifikatoren Eine verbreitete Variante benutzt ein konstantes r für die Folge rk. Diese Variante wird angewendet, wenn sich die Stichprobenverteilung mit dem Index k ändert. Sie konvergiert jedoch nicht genau gegen die MSE-Lösung. Hayk konnte jedoch 1996 zeigen, daß wenn 0 < r < 2/spur{R}, dann E wˆ (k ) wMSE und 2 ˆ E w(k ) wMSE const Es stellt sich heraus, dass, je kleiner der Wert von r ist, die MSE Lösung umso besser approximiert wird, aber die Konvergenzgeschwindigkeit umso kleiner ist. Vorlesung "Intelligente Systeme" 129 Lineare Klassifikatoren Schätzalgorithmus mittels Quadratfehlersummen Vorlesung "Intelligente Systeme" 130 Lineare Klassifikatoren Schätzung mittels Summe der Fehlerquadrate Ein anderes Kriterium für die Konstruktion eines optimalen linearen Klassifikators ist die Minimierung der Summe der Fehlerquadrate über die Trainingsstichprobe. Die Kostenfunktion lautet dann: N T J ( w) ( yi xi w) 2 i 1 Die Fehlerquadrate zwischen den gewünschten und den tatsächlichen Klassifikatorausgängen werden über alle verfügbaren Trainingsvektoren der Stichprobe aufsummiert, wodurch die Notwendigkeit der expliziten Kenntnis der zugrundeliegenden Verteilungsfunktionen vermieden wird. Die Minimierung obiger Gleichung bezüglich w ergibt: N T ˆ N T ˆ ! xi ( yi xi w) 0 xi xi w xi yi i 1 i 1 i 1 N Mit x1T T x X 2 und T x N y1 y2 y wird yN N T T xi xi X X i 1 Vorlesung "Intelligente Systeme" N und T x y X y i i i 1 131 Lineare Klassifikatoren Die Minimum-Bedingung kann umformuliert werden als: 1 T T ˆ T ˆ X X w X y w X X X y T Matrix XTX wird bezeichnet als “Stichproben-Korrelationsmatrix”. Matrix (XTX)-1XT ist die Pseudoinverse von Matrix X und wird mit X+bezeichnet. X+ ist nur dann sinnvoll, wenn XTX invertierbar ist, d.h. wenn X den Rang l besitzt. X+ ist eine Verallgemeinerung der Inversen einer invertierbaren quadratischen Matrix: Wenn X eine invertierbare quadratische Matrix ist, dann ist X+ = X-1. Dann ist der geschätzte Gewichtsvektor die Lösung des linearen Gleichungssystems Xw = y. Wenn es mehr Gleichungen als Unbekannte gibt, d.h., wenn N > l, dann ist die Lösung, die man mit der Pseudoinversen erhält, diejenige, die die Summe der Fehlerquadrate minimiert. Es kann ferner gezeigt werden, daß die Lösung mit der Summe der Fehlerquadrate gegen die MSE-Lösung strebt, wenn N gegen unendlich geht. Vorlesung "Intelligente Systeme" 132 Lineare Klassifikatoren Mehrklassen-Verallgemeinerung Vorlesung "Intelligente Systeme" 133 Lineare Klassifikatoren Mehrklassen-Verallgemeinerung T Konstruiere N lineare Trennfunktionen wi x i=1,...,N wobei der gewünschte Ausgang lautet y( x ) y 1 wenn x ci und y 0 sonst Mit dem MSE Kriterium: 2 J ( w) E y x T wi , wˆ i arg min J ( w ) w Wenn wir in diesem Fall N=2 wählen gibt die Entscheidungs-Hyperebene w x (w1 w2 ) x die gewünschten Antworten +-1 für die entsprechende Klassenzugehörigkeit. Definiert man den Vektor der gewünschten Ausgänge für einen gegebenen Merkmalsvektor x als y=(y1, ,yN), wobei yi=1 für die Klasse von Vektor x und y=0 sonst. Es sei ferner Matrix W zusammengesetzt aus Gewichtsvektoren wi als Spalten. W w1 ,..., wN Dann kann das MSE Kriterium verallgemeinert werden als Minimierung der Norm von y-WTx: T ˆ W arg min E y W x W 2 N 2 arg min E ( yi wi x ) W i 1 Dies ist gleichbedeutend mit N unabhängigen MSE Minimierungsaufgaben, welche mit den bereits vorgestellten Methoden gelöst werden können. Vorlesung "Intelligente Systeme" 134 Lineare Klassifikatoren Aufstieg und Fall des Perzeptrons 1957 – Frank Rosenblatt entwickelt Konzept des Perzeptron 1958 – Konzept-Vorstellung 1960 – Konzept-Umsetzung an der Cornell University, Ithaca, New York (USA) 1962 – Zusammenfassung der Ergebnisse in „Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms” 1969 – Beweis durch Marvin Minsky und Seymour Papert, dass ein einstufiges Perzeptron den XOR-Operator nicht darstellen kann. Vorlesung "Intelligente Systeme" 135 Nicht-lineare Klassifikatoren Das XOR-Problem Das Zweischicht-Perzeptron Eigenschaften des Zweischicht-Perzeptrons Prozedur zum Auffinden geeigneter Abbildungen mit Perzeptrons Der Backpropagation-Algorithmus Bemerkungen zum Backpropagation-Algorithmus Freiheitsgrade beim Backpropagation-Algorithmus Vorlesung "Intelligente Systeme" 136 Nicht-lineare Klassifikatoren In vielen praktischen Fällen sind auch optimale lineare Klassifikatoren unzureichend. Einfachstes Beispiel: Das XOR Problem. Bool´sche Operationen können als Klassifikationen aufgefasst werden: Abhängig vom binären Eingangsvektor ist der Ausgang x ( x1 , x2 ,, xl ), xi 0,1 entweder 1 (Klasse A) oder 0 (Klasse b). X1 0 0 1 1 X2 0 1 0 1 AND(X1, X2) KlasseOR(X1, X2) Klasse XOR(X1, X2) Klasse 0 B 0 B 0 B 0 B 1 A 1 A 0 B 1 A 1 A 1 A 1 A 0 B x2 1 0 x2 x2 B A B B 1 1 x1 0 A A B A 1 Vorlesung "Intelligente Systeme" 1 x1 0 A B B A 1 x1 137 Nicht-lineare Klassifikatoren Das zweischichtige Perzeptron Wir betrachten zunächst das OR-Gatter: x2 Die OR-Separierung wird dargestellt durch folgende Perzeptron-Struktur: x1o 1 1 A A S 1 A B x1 0 f x1 x2o -1/2 Das XOR Gatter x2 + + A - 1 B A B 0 1 Eine offensichtliche Lösung des XOR-Problems wäre, zwei Entscheidungslinien g1(x) and g2(x) einzuzeichnen. Dann ist Klasse A auf der - Seite von g1(x) und auf der + Seite von g2(x) und Klasse B auf der + Seite von g1(x) und auf der - Seite von g2(x). Eine geeignete Kombination der Ergebnisse der beiden x1 linearen Klassifikatoren würde also die Aufgabe erfüllen. g1(x) g2(x) Vorlesung "Intelligente Systeme" 138 Nicht-lineare Klassifikatoren Anderer Blickwinkel als Basis für Verallgemeinerung: Realisierung zweier Entscheidungslinien (Hyperebenen) durch Training zweier Perzeptrons mit Eingängen x1, x2 und entsprechend berechneten Gewichten. Die Perzeptrons wurden trainiert, die Ausgänge yi = f(gi(x)), i=1,2 zu liefern, Aktivierungsfunktion f: Sprungfunktion mit Werten 0 und 1. In der folgenden Tabelle sind die Ausgänge mit ihren entsprechenden Eingängen gezeigt: (x1 x2) (y1 y2) Klasse (0 0) (0 0) B (0) (0 1) (1 0) A (1) (1 0) (1 0) A (1) (1 1) (1 1) B (0) Betrachtet man (x1, x2) als Vektor x und (y1, y2) als Vektor y, definiert dies eine Abbildung von Vektor x auf Vektor y. Entscheidung über die Zugehörigkeit zu Klasse A oder B anhand der transformierten Daten y: y2 B 1 B x1 0 Die Abbildung überführt linear nicht separierbares Problem im Ursprungsraum in ein linear separierbares im Bildraum. A y1 Vorlesung "Intelligente Systeme" 139 Nicht-lineare Klassifikatoren Dies führt zum Zweischicht-Perzeptron, welches das XOR-Problem löst: x1o 1 1 1 x2o 1 S f 1 -1/2 -2 S S f f f -1/2 Sprungfunktion 1 -3/2 0 0 S Dieses kann weiter verallgemeinert werden auf das allgemeine Zweischicht-Perzeptron oder Zweischicht-Feedforward-Netzwerk: Dabei bezeichnet jeder Knoten folgende x1o w1 Struktur: O y1 . x2o O y2 . O . f . S w . N . O yM . xNo w0 Vorlesung "Intelligente Systeme" 140 Nicht-lineare Klassifikatoren Eigenschaften des Zweischicht-Perzeptrons x1o 1 S 1 1 x2o f y1 1 -1/2 S 1 S f -2 f -1/2 y2 -3/2 Die erste Schicht führt eine Transformation der Bereiche des Eingangsraumes (x1,x2) auf den + und - Seiten der geraden Entscheidungslinien g1: x1+x2-1/2=0 und g2 : x1+x2-3/2=0 durch auf die Vertizes (Ecken) des Einheitsquadrates im Ausgangsraum (y1,y2). x2 y2 + Die zweite Schicht führt eine Abbildung der Bereiche des + B B A 1 (y1,y2)-Raumes auf den + - 1 + und - Seiten der geraden Entscheidungslinie A B A B g: y1-2y2-1/2=0 durch auf die 0 x1 1 x1 0 y 1 1 Ausgangswerte 0 und 1. g (x) 1 g2(x)Vorlesung "Intelligente Systeme" 141 Nicht-lineare Klassifikatoren x1o O y1 O y2 . . O yM x2o . . . xNo O Neuronen der ersten Schicht: Abbildung des Eingangsraumes auf die Vertizes eines Hyperkubus im M-dimensionalen Raum der Ausgangswerte der versteckten Neuronen. =>Jeder Eingangsvektor x wird auf einen binären Vektor y abgebildet. Komponenten yi des Abbild-Vektors y von Vektor x werden durch den Gewichtsvektor wi bestimmt. Befindet sich x auf der positiven Seite der Ebene, welche durch wi definiert ist, hat yi den Wert 1 und wenn x auf der negativen Seite der Ebene liegt, die durch wi definiert ist, hat yi den Wert 0. Wir betrachten den Fall dreier versteckter Neuronen: Drei Hyperebenen g1, g2, g3: g1 + 111 + g2 001 + g - 011 010 000 110 Der Merkmalsraum wird in Polyeder unterteilt (Volumina, die durch Entscheidungs-Hyperebenen begrenzt werden), welche auf die Vertizes eines dreidimensionalen Kubus abgebildet werden, welche durch Tripel der binären Werte y1, y2, y3 definiert werden. 011 100 001 111 101 3 110 000 100 Zweite Schicht: Entscheidungshyperebene, welche die Vertizes in zwei Klassen aufteilt. Im vorliegenden Fall werden die Gebiete 111, 110, 101 und 100 in die gleiche Klasse eingeteilt. Vorlesung "Intelligente Systeme" 142 Nicht-lineare Klassifikatoren Ein Zweischicht-Perzeptron kann Klassen unterteilen, die aus Vereinigung polyedrischer Bereiche bestehen. Liegen Vereinigungen solcher Bereiche vor, wird eine weitere Schicht benötigt. Merkmalsraum O y1,2 O y2,2 . . O yL,2 O y1,1 O y2,1 . . O yM,1 x2o . . . xNo O : O Klassenzugehörigkeitsraum x1o Das Perzeptron kann auch erweitert werden, um Mehrklassenprobleme zu lösen. Das Mehrschicht-Perzeptron löst alle Klassifikationsaufgaben, bei denen die Klassen im Merkmalsraum durch Vereinigungen von Polyedern, Vereinigungen solcher Vereinigungen, ..., gebildet werden, wenn die entsprechende Anzahl von Schichten zur Verfügung steht. Class wj p3 Gk Class wk Class wl p1 p2 Gl p4 Vorlesung "Intelligente Systeme" m1 m2 m3 Merkmalsraum Klassenzugehörigkeitsraum Gj 143 Nicht-lineare Klassifikatoren Anmerkungen: Struktur zur nicht-linearen Abbildung von Merkmalsvektoren auf Klassenzugehörigkeitsvektoren: Das Mehrschicht-Perzeptron. Verbleibende, noch zu bestimmenden Freiheitsgrade: Anzahl der Schichten, Anzahl der Neuronen pro Schicht, Aktivierungsfunktion, Gewichtswerte. Verbleibende Frage: Bei gegebenen Merkmalen und bekannten Klassenzugehörigkeiten der StichprobenVektoren: Welches ist die beste Anordnung von Neuronen und Gewichtsvektoren, die eine gegebene Klassifikationsaufgabe lösen? Hilfe seitens der Mathematik: Für jedes kontinuierliche Abbildungsproblem kann ein Zweischicht-Perzeptron mit einer nicht-linearen Aktivierungsfunktion und einer hinreichenden Anzahl Neuronen in der versteckten Schicht gefunden werden, welches die Abbildung mit beliebiger Genauigkeit annähert. => Freiheit, einen Satz von Aktivierungsfunktionen zu wählen, der eine einfache Lösung ermöglicht. Vorlesung "Intelligente Systeme" 144 Nicht-lineare Klassifikatoren Auffinden einer geeigneten Abbildung mit Perzeptrons Einmal wieder Optimierungsprozedur: Minimierung der Differenz zwischen realem Ausgang des Perzeptrons (vorausgesagte Klassenzugehörigkeit) und dem gewünschten Ausgang entsprechend der bekannten Klassenzugehörigkeiten der verfügbaren Stichprobe. Definition einer Kostenfunktion der Differenz zwischen realem und gewünschtem Ausgang. z.B. Summe der Fehlerquadrate. Minimierung der Kostenfunktion bezüglich der Perzeptron-Parameter. Vereinfachung: Definiere eine Aktivierungsfunktion. Dann braucht die Minimierung nur bezüglich der Gewichtswerte durchgeführt werden. Minimierung impliziert die Nutzung der Ableitungen der Aktivierungsfunktion. Wird die Sprungfunktion benutzt, tritt eine Unstetigkeit in der Ableitung auf. Wir ersetzen daher die Sprungfunktion durch die stetig differenzierbare logistische Funktion. f f ( x) 1 1 e ax Die logistische Funktion ist eine aufgeweichte Sprungfunktion, wobei a die Steigung bei x=0 bestimmt und 1 lim f Sprungfunktion a x Damit ist die Klassenzugehörigkeit nicht mehr scharf 0 oder 1. Vorlesung "Intelligente Systeme" 145 Nicht-lineare Klassifikatoren Nun kann der “geeignetste” Klassifikator durch Minimierung einer Kostenfunktion bezüglich der Gewichtswerte gefunden werden. Geometrische Betrachtungsweise: Alle Gewichte (aller Schichten) spannen einen Raum auf. Die Kostenfunktion bildet dann eine Fläche über diesem Raum. => Globales Minimum dieser Fläche für die gegebene Stichprobe gesucht. Da nicht-lineare Aktivierungsfunktionen vorliegen, wird zur Suche ein iteratives Schema benutzt. Der verbreitetste Ansatz ist die Gradientenabstiegsmethode: Starte mit einem Zufalls-Gewichtsvektor w. Berechne den Gradienten der Fläche bei w. Bewege w in Richtung entgegen dem Gradienten. Wiederhole die obigen Schritte, bis ein Minimum erreicht ist, d.h. der Gradient einen Schwellwert unterschreitet. Es sei w der Gewichtsvektor von Neuron n in Schicht l: wnl 0 l w wnl n1 dann ist wl nM wnl (k 1) wnl (k ) Dwnl Vorlesung "Intelligente Systeme" 146 Nicht-lineare Klassifikatoren Korrektur-Inkrement D mit Kostenfunktion J: J Dwnl l wn Neuron 2 in Schicht 3 x1o x2o . . . xNo l=1 O n2,1 O n2,2 . . O n2,M O n3,1 O n3,2 . . O n3,K O : O l=L wnl 0 l w wnl n1 mit n 2 und l 3 wl nM k 1 1 M 2 e: Summe der Fehlerquadrate über alle M Ausgangsneuronen: e (k ) ym (k ) yˆ m (k ) 2 m 1 K Aktivierung Neuron n in Schicht l J e (k ) e (k ) e (k ) vnl Kettenregel: o wnl k 1 wnl wnl vnl wnl w1 l v j (k ) l 1 o w2 y y1 (k ) l n . w . j1 f S A vnl l 1 l l l 1 l vn wna ya wn 0 wN l l l 1 y (k ) . w y ( k ) v j (k ) n a 1 n . l 1 l 1 o w j 0 w0 Kostenfunktion: Summe der Abweichungen des tatsächlichen vom gewünschten Ausgang K für alle K Stichprobenvektoren: J e ( k ) Vorlesung "Intelligente Systeme" 147 Nicht-lineare Klassifikatoren o o o . . . o n n Schicht l . . Schicht l-1 l 1 n y nl 1 wljn o . . o f Wn0l-1 j n lj f y lj wj0l Neuron n aus Schicht l-1. Ausgang für Stichprobenvektor k: ynl-1(k). Gewichtswert zu Neuron j aus der nachfolgenden Schicht l: wjnl. Dann ist das Argument dieses Neurons j aus Schicht l: nl 1 nl 1 v (k ) w y (k ) w wljn ynl 1 (k ) mit l j n 1 l l 1 jn n l j0 n 0 In der Ausgangsschicht ist l L, y nL (k ) yˆ n (k ) An der Eingangsschicht gilt l 1, y1n (k ) xn (k ) y0l (k ) 1 l , k e (k ) l d (k ) n l v n (k ) K Beziehung gilt für jede Dwnl d nl (k ) y l 1 (k ) Diese differenzierbare Kostenfunktion. Definition für gegebenes Abweichungsmaß e: Schließlich erhalten wir: k 1 Vorlesung "Intelligente Systeme" 148 Nicht-lineare Klassifikatoren Die Berechnungen beginnen an der Ausgangsschicht l=L und propagieren rückwärts durch die Schichten l=L-1, L-2, ..., 1. Bei Benutzung des Quadratfehler-Distanzmaßes erhalten wir: (1) l = L: Fehler für Muster k an Ausgangsschicht Aus 1 M e (k ) ym (k ) yˆ m (k ) 2 2 m 1 Aktivierungsfunktion 2 1 M L ˆ e ( k ) f ( v ( k )) y ( k ) wird m m 2 m 1 Ableitung der Aktivierungsfunktion Von e (k ) l d (k ) n l v n (k ) folgt d jL (k ) vmL (k ) yˆ m (k ) f vmL (k ) l l 1 (2) l < L: Schwieriger wegen Einfluss von v s ( k ) auf alle v s (k ) der nächsten Schicht ml l l ml v (k ) v ( k ) e ( k ) e ( k ) l 1 l m m Nochmals Kettenregel: d ( k ) d ( k ) n n vnl 1 (k ) v nl 1 (k ) m 1 v ml (k ) v nl 1 (k ) m 1 Nach längerer Algebra erhält man folgende Gleichung: d l 1 m nl l l l 1 (k ) d n (k ) wnm f v m (k ) n1 Dies vervollständigt den Gleichungssatz des Backpropagation Algorithmus. Vorlesung "Intelligente Systeme" 149 Nicht-lineare Klassifikatoren Der Backpropagation Gleichungssatz d jL (k ) vmL (k ) ym (k ) f vmL (k ) d jL (k ) emL (k ) f vmL (k ) mit emL (k ) vmL (k ) ym (k ) d l 1 m nl l l l 1 (k ) d n (k ) wnm f v m (k ) n1 d l 1 m (k ) e l 1 m f v (k ) mit e l 1 m Fehler-Rückpropagierung d mL (k ) e mL f (v mL (k )) d ml 1 (k ) e ml 1 f v ml 1 (k ) nl l e ml 1 d nl (k ) wnm l 1 m nl l d nl (k ) wnm n 1 Gewichtsmodifikation l l l wn (k 1) wn (k ) Dwn K l l 1 l Dwn d n (k ) y (k ) k 1 n 1 Vorlesung "Intelligente Systeme" 150 Nicht-lineare Klassifikatoren Der Backpropagation Algorithmus Unter der Annahme der logistischen Funktion als Aktivierungsfunktion: f ( x) 1 1 e ax f ( x) f ( x)(1 f ( x)) 1. Initialisierung Initialisiere die Gewichte des Netzwerks mit kleinen Zufallszahlen. Benutze z.B. einen Pseudozufallszahlengenerator. 2. Vorwärts-Berechnung Berechne für jeden Merkmalsvektor x(i) der Trainingsmenge alle vjl(i), yjl(i)=f(vjl(i)) und die Kostenfunktion J sowie djl(i) für die momentanen Schätzwerte der Gewichte. 3. Rückwärts-Berechnung Berechne für jedes i die djl-1(i) und aktualisiere die Gewichte für alle Schichten entsprechend: wlj (new) wlj (old ) Dwlj nl l l 1 l Dw j d n (i ) y (i ) n 1 Wiederhole Schritte 2 und 3, bis der Wert von J zufriedenstellend klein ist. Vorlesung "Intelligente Systeme" 151 Nicht-lineare Klassifikatoren Bemerkungen zum Backpropagation Algorithmus Ausgangspunkt Mehrschicht-Perzeptrons mit Stufenfunktionen als Aktivierungsfunktionen: Operatoren zur Aufteilung des Merkmalsraums in Volumina, welche Klassenzugehörigkeiten repräsentieren. Volumina waren allgemeine Vereinigungen von Polyedern, begrenzt durch Entscheidungs-Hyperebenen. Lösungsweg Für eine gegebene endliche Stichprobe (Merkmalsvektoren mit bekannter Klassenzugehörigkeit) existiert i.A. eine unbegrenzte Anzahl möglicher MehrschichtPerzeptron-Realisierungen, welche die Klassifikationsaufgabe lösen. Suche nach einer eindeutigen (der besten) Lösung: Minimum einer Kostenfunktion; Wahl: Fehlerquadratsumme. Für mathematische Formulierung: Ersatz der Stufenfunktion durch die logistische Funktion als Aktivierungsfunktion. Optimierungsprozedur zur Bestimmung der Gewichtwerte für eine gegebene Stichprobe: den Backpropagation Algorithmus. Allgemeingültigkeit Satz von Kolmogoroff aus der Mathematik: Abbildungsoperatoren mit einer versteckten Schicht und nicht-linearer Abbildungsfunktion sind in der Lage, jegliche stetig differenzierbare Abbildung zu realisieren. Daraus folgt, dass wir eine einfache Methode gefunden haben, einen universellen Mustererkenner zu konstruieren. Vorlesung "Intelligente Systeme" 152 Nicht-lineare Klassifikatoren Offene Fragen zum Backpropagation Algorithmus Wie komme ich zu einer guten Netzwerkstruktur ? J Wie kann ich die Konvergenzgeschwindigkeit optimieren ? m Wie kann ich vermeiden, in lokalen Minima der Kostenfunktion steckenzubleiben ? J Wie präsentiere ich die Trainingsstichprobe ? Update nach jedem Trainingspaar, Epochen-Lernen, sequentielle oder zufällige Reihenfolge ? w Wann höre ich mit dem Training auf ? Gibt es bessere Kostenfunktionen ? Gibt es Alternativen für die Architektur und die Aktivierungsfunktion ? Vorlesung "Intelligente Systeme" 153 Nicht-lineare Klassifikatoren Wahl der Netzwerkgröße und -struktur Wie soll man die geeignete Anzahl der Neuronen und Schichten bestimmen? Wenn eine endliche Trainingsstichprobe von Paaren gegeben ist {x1,y1, x2,y2, ..., xN,yN}, dann sollte die Anzahl der freien Parameter (hier synaptische Gewichte) 1) groß genug sein, um eine angemessene Klassentrennung modellieren zu können 2) klein genug sein, damit nicht die Möglichkeit besteht, die Unterschiede zwischen Paaren derselben Klasse (Look-up Tabelle) zu lernen. x2 * * +* * + * * Hohe Anzahl freier Parameter * * + + * + + + Niedrige Anzahl freier Parameter + + x Wenn die Anzahl freier Parameter groß1 ist, tendiert das Netz dazu, sich an die speziellen Details des Trainingsdatensatzes anzupassen (Übertrainieren) und verliert seine Generalisierungsfähigkeit. Das Netz sollte die kleinst mögliche Größe besitzen, um sich den größten Regelmäßigkeiten in den Daten anzupassen und die kleineren zu ignorieren, die von Rauschen herrühren könnten. Zur Bestimmung der Netzgröße gibt es auch systematische Methoden. Vorlesung "Intelligente Systeme" 154 Nicht-lineare Klassifikatoren Methoden zur systematischen Bestimmung der Netzgröße Algebraische Schätzung Ein Mehrschicht-Perzeptron mit Eingangsraum-Dimensionalität d und einer versteckten Schicht mit N Neuronen kann maximal M polyedrische Gebiete bilden, wobei 0 für N m N N! sonst . m m!( N m)! Für das XOR-Problem mußten wir drei Gebiete unterscheiden, d.h. M=3 und d=2. Mit obiger Gleichung erhält man für N=1 M=2 und für N=2 ergibt sich M=4, was bedeutet, daß eine versteckte Schicht mit zwei Neuronen notwendig und hinreichend ist. N M , m 0 m d Netzpruning Anfangs wird ein großes Netzwerk für das Training gewählt und danach die Anzahl der freien Parameter sukzessive entsprechend einer ausgewählten Regel (z.B. KostenfunktionsRegularisierung) reduziert. Die Kostenfunktionsregularisierung schließt in die Kostenfunktion einen Bestrafungsterm ein. Dieser kann z.B. gewählt werden als: 2 M K wk 2 2 J e (i) le p ( w), e p ( w) h( wk ), h( wk ) 2 1 wk i 1 k 1 wobei K die Gesamtzahl der Gewichtswerte im Netzwerk und l der Regularisierungsparameter ist. Es gibt verschiedene Pruning-Techniken, die auf ähnlichen Grundideen aufbauen. Vorlesung "Intelligente Systeme" 155 Nicht-lineare Klassifikatoren Konstruktive Techniken Als Ausgangspunkt wird ein kleines Netzwerk gewählt, dem aufgrund entsprechend angepaßter Lernregeln sukzessive Neuronen hinzugefügt werden. Fahlmann (1990) schlug die cascade correlation Konstruktionstechnik für neuronale Netze mit einer versteckten Schicht und sigmoider Aktivierungsfunktion vor. Start: nur Eingangs- und Ausgangsneuronen. Sukzessives Hinzufügen versteckter Neuronen: Jeweils mit dem bestehenden Netzwerk mit zwei Typen von Gewichten verbunden: Typ 1: verbindet das neue Neuron mit den Eingangsneuronen sowie mit den Ausgängen der zuvor hinzugefügten versteckten Neuronen. Die entsprechenden Gewichtswerte werden dann trainiert, um die Korrelation zwischen der Sequenz der Ausgangswerte des neu hinzugefügten Neurons und der Restfehlersequenz des Netzwerkausgangs (für die Trainingsvektormenge) zu maximieren. Diese Gewichtswerte werden dann eingefroren. Typ 2: verbindet den Ausgang des neuen Neurons mit den Ausgangsneuronen des Netzwerks. Nach jedem derartigen Hinzufügen eines Neuron: Training des gesamten Satzes der Typ2Gewichte, um die Quadratfehlersumme zu minimieren. Neue Neuronen werden solange hinzugefügt, bis die Kostenfunktion spezifizierte Vorgaben erfüllt. Vorlesung "Intelligente Systeme" 156 Nicht-lineare Klassifikatoren Konstruktive Techniken cascade correlation Konstruktionstechnik 1. Start: nur Eingangs- und Ausgangsneuronen 2. Training bis Minimum SSE 3. Schleife bis SSE < Schwellwert 3.1 Hinzufügen neues hidden Neuron 3.2 Verbinde Eingänge neues Neuron mit Eingangsneuronen und Ausgängen der alten hidden Neuronen mit Typ1-Gewichten. 3.3 Trainiere Typ1-Gewichte neues Neuron, bis die Korrelation zwischen SSE des alten Netzwerks und Ausgang des neuen Neurons maximal ist. 3.4 Verbinde Ausgang neues Neuron mit Eingängen der Ausgangsneuronen mit Typ2-Gewichten. 3.4 Trainiere Typ2-Gewichte aller versteckten Neuronen, bis SSE des Netzwerks minimal. Vorlesung "Intelligente Systeme" x1 x2 . . xM O O . . O O Typ1-Gewicht Typ2-Gewicht x1 x2 . . xM O O . . O O x1 x2 . . xM O O . . O O O O O 157 Nicht-lineare Klassifikatoren Konvergenzverhalten und Beschleunigung Der Backpropagation Algorithmus ist eine Variante der Gradienteabstiegsmethoden, speziell für Mehrschichtstrukturen. Er hat damit dieselben Nachteile wie sein Original. langsam J oszillierend J Dwnl l wn steckengeblieben w Es gibt mehrere Ansätze, diese Probleme zu überwinden. Hinzufügen eines Impulsterms nl l l 1 l l l l l w j (neu ) w j (alt ) Dw j , Dw j Dw j (alt ) d n (i) y (i) n1 Der Impulsterm dämpft das Oszillationsverhalten und beschleunigt die Konvergenz. Er fügt aber auch einen neuen Parameter hinzu, den Impulsfaktor, der den Einfluß des alten Gewichtsvektors auf die Gestalt des neuen Gewichtsvektors gewichtet. Vorlesung "Intelligente Systeme" 158 Nicht-lineare Klassifikatoren Beschleunigung mit Rprop Die Grundidee besteht darin, für die Lernrate µ einen adaptiven Wert zu verwenden, der vom Unterschied des Kostenfunktionswertes zwischen zwei aufeinanderfolgenden Trainingsschritten abhängt: Nimmt die Kostenfunktion ab, oder bleibt sie unverändert, dann wird die Lernrate um einen Faktor > 1 erhöht. Wenn J (t ) 1 dann (t ) ri (t 1) J (t 1) Steigt die Kostenfunktion an um mehr als einen bestimmten Faktor, dann wird die Lernrate mit einem Faktor < 1 verringert. Wenn J (t ) c dann (t ) rd (t 1) J (t 1) Im Zwischenbereich bleibt die Lernrate gleich. Wenn 1 J (t ) c dann (t ) (t 1) J (t 1) In der Praxis sind typische Werte ri=1.05, rd=0.7, c=1.04 Vorlesung "Intelligente Systeme" 159 Nicht-lineare Klassifikatoren Gegenmaßnahmen bei Steckenbleiben im lokalen Minimum Bleibt auch nach einer großen Anzahl von Trainingsepochen die Kostenfunktion auf einem unbefriedigend hohen Niveau, kann davon ausgegangen werden, daß die Gradientenabstiegsmethode in einem lokalen Minimum steckengeblieben ist. J Anzahl der Epochen Man kann dann zuerst versuchen, das Training mit einer neuen Zufallsgewichtsverteilung zu wiederholen. Wenn auch dies nicht hilft, kann ein weiteres Neuron in einer versteckten Schicht hinzugeügt werden, um neue Dimensionen im Raum der Gewichtswerte hinzuzufügen, in denen die Gradientenmethode einen Weg aus dem lokalen Minimum finden kann. Vorlesung "Intelligente Systeme" 160 Nicht-lineare Klassifikatoren Präsentation des Trainingsdatensatzes Der Trainingsdatensatz kann in verschiedener Reihenfolge angeboten werden. Die Neuberechnung der Gewichte kann mit unterschiedlicher Strategie erfolgen. Den Daten kann Rauschen hinzugefügt werden. Die Verteilung der Trainingsdaten kann verändert werden. Neuberechnung der Gewichte: Batch Modus: Nach Präsentation aller Trainingspaare (Epochenlernen) Mittelungsprozess -> besseres Konvergenzverhalten Pattern Modus: Nach jeder Präsentation eines Trainingspaares Stärkerer Zufallscharakter -> geringere Gefahr des Steckenbleibens Überlagerung von Rauschen: Eine kleine zufällige Störung der Eingangsvektoren kann die Generalisierungsfähigkeit des Netzwerks verbessern. Reihenfolge der Präsentation des Trainingsdatensatzes: Die Zufallsauswahl bei der Präsentationsreihenfolge glättet die Konvergenz und hilft, aus Regionen um ein lokales Minimum herauszuspringen. Vervielfachung der Trainingspaare: Wenn die Klassen in der Stichprobe durch sehr unterschiedliche Anzahlen von Trainingspaaren repräsentiert werden, kann die Konzentration des Netzes auf die stark besetzten Klassen vermieden werden, indem Kopien der Trainingspaare der unterbesetzten Klassen der Stichprobe hinzugefügt werden. Vorlesung "Intelligente Systeme" 161 Nicht-lineare Klassifikatoren Abbruch des Lernvorgangs Die optimale Leistung ist erreicht, wenn Die Kostenfunktion minimal für den Trainingsdatensatz ist. Das Netzwerk nicht übertrainiert ist. Aufteilung des Trainingsdatensatzes in Lerndatensatz: Zur Neuberechnung der Gewichtswerte Validierungsdatensatz: Nur zur Überprüfung der aktuellen Netzleistung Beobachte die Entwicklung der Kostenfunktionswerte jeweils für den Lern- und den Vailidierungsdatensatz. J Validierungsdatensatz Lerndatensatz Epochenanzahl Wenn die Anzahl der Gewichtswerte groß genug gewählt wurde, kann der Fehler für den Lerndatensatz beliebig klein gemacht werden. Dies führt zum Verlust der Generalisierungsfähigkeit: Die Kostenfunktion des Validierungsdatensatzes nimmt nach einem Minimum wieder zu. Die optimale Leistung eines gewählten Netzwerks wird also am Minimum der Kostenfunktion des Validierungsdatensatzes erreicht. Vorlesung "Intelligente Systeme" 162 Nicht-lineare Klassifikatoren Kostenfunktion Alternativen Bislang Kostenfunktion vom Typ „quadratischer Fehler“. Mögliche Probleme: 1. „Lernfokussierung“ und Ausreisser-Empfindlichkeit Fehler werden an den Ausgangsknoten zuerst quadriert und dann aufsummiert. Folge: große Fehlerwerte -> höherer Einfluß auf das Lernen als kleine. Ausgänge mit großen dynamischen Bereichen der Soll-Ausgangswerte werden stärker berücksichtigt. 2. Lokale Minima Gradientenabstiegsmethode kann in lokalen Minima hängen bleiben. Lösung: Es gibt eine Klasse von Kostenfunktionen, well-formed functions, die sicherstellen, daß der Gradientenabstiegsalgorithmus zu einer eindeutigen Lösung konvergiert, welche alle Lerndatensätze korrekt klassifiziert. Z.B. cross-entropy Kostenfunktion: N J i 1 kL y (i) ln yˆ (i) 1 y (i)ln 1 yˆ (i) k k 1 N oder J i 1 k k k ln yˆ k (i) 1 yˆ k (i ) y ( i ) 1 y ( i ) ln k k ln yk (i) 1 yk (i ) k 1 kL Diese hängt nur von relativen Fehlern ab und gibt Klassen mit niedrigem und hohem dynamischen Bereich das gleiche Gewicht. Vorlesung "Intelligente Systeme" 163 Nicht-lineare Klassifikatoren Alternative Aktivierungsfunktionen Ausgangspunkt für die Konstruktion nicht-linearer Klassifikatoren war das XOR-Problem. Lösung: Vektor-Abbildung x auf y, welche das in x nicht-lineare Problem in ein linear separierbares in y überführte. y f g ( x ) 1 1 F: Aktivierungsfunktion und x y mit y y f g ( x ) gi(x): Linearkombination der Eingänge 2 2 eines jeden Neurons. Verallgemeinerung: Merkmalsvektoren im d-dimensionalen Raum Rd, die zu zwei Klassen gehören, die nicht linear trennbar sind. Gegeben seien k nicht-lineare Aktivierungsfuktionen f1, f2, ..., fk, welche eine Abbildung definieren: x Rl y R k mit f1 ( x ) f ( x ) y 2 f k ( x ) Wir suchen dann nach einer Menge von Funktionen f1, f2, ..., fk, so dass die Klassen linear separierbar sind im kdimensionalen Raum der Vektoren y durch eine Hyperebene, so dass Unter der Annahme, dass die beiden Klassen im Ursprungs- w0 w y 0 x c1 raum durch eine nicht-lineare Hyperfläche G(x)=0 trennbar w w y 0 x c2 0 waren, dann sind die beiden Relationen rechts äquivalent mit einer Approximation der nicht-linearen Fläche G(x) mit einer Linearkombination der f(x). k G( x ) w0 w j f j ( x ) Dies ist ein Funktionenapproximationsproblem mit einem Satz j 1 Funktionen einer ausgewählten Funktionenklasse. Vorlesung "Intelligente Systeme" 164 Nicht-lineare Klassifikatoren Dies entspricht einem Zweischicht-Netzwerk mit Aktivierungsfunktionen f1, f2, ..., fk. Die Äquivalenz wird leicht erkannt im (künstlichen) Fall jeweils eines Ein- und Ausgangsneurons: x O w1,1 w1,2 . w1,M O f1 w 2,1 O f2 w 2,2 . . w . 2,M O fM M O y w2, j f j (w1, j x w0, j ) y j 1 Das bislang betrachtete Perzeptron benutzte als Funktionenklasse die logistischen Funktionen: y x w0 Zwei weitere Klassen haben in der Mustererkennung spezielle Bedeutung: Polynome Gaußfunktionen L L 1 g ( x ) w0 wl xl l 1 L w l 1 m l 1 Polynomklassifikatoren L x xm w x lm l l 1 2 ll l L g ( x ) w0 wl xl e ( x cl )( x cl ) 2 2 l 1 Radiale-Basisfunktionen-Netze Vorlesung "Intelligente Systeme" 165 Nicht-parametrische Methoden Nächster-Nachbar-Klassifikator Nächste-Nachbar-Regel Gegeben sei eine Stichprobe aus N Mustervektoren (Prototypen) und zugehörigen Klassenzugehörigkeiten (Label) {( x1 , C1 ), ( x2 , C2 ),..., ( xN , CN )} Ein unbekanntes Muster ist zu klassifizieren. Regel: Es wird ihm die Klasse des ihm nächstliegenden Prototypen zugeordnet. Klasse 1 Wirkung im Merkmalsraum: Aufteilung in Voronoi-Zellen Klasse 2 Große Zellen (grobe Auflösung) wo Musterdichte gering Kleine Zellen (feine Auflösung) wo Musterdichte hoch Graphik aus Duda, Hart, Stork: Pattern Classification 2nd edition, Wiley-Interscience Vorlesung "Intelligente Systeme" 166 Nicht-parametrische Methoden K-Nächste-Nachbar-Klassifikator Gegeben sei eine Stichprobe aus N Mustervektoren (Prototypen) und zugehörigen Klassenzugehörigkeiten (Label) {( x1 , C1 ), ( x2 , C2 ),..., ( xN , CN )} Ein unbekanntes Muster ist zu klassifizieren. Regel: Eine Hyperkugel wird um herum solange vergrößert, bis k Prototypen darin enthalten sind. Es wird die Klasse der einfachen Mehrheit dieser k nächsten Prototypen zugeordnet. Klasse 1 Klasse 2 Zwei-dmensionaler Merkmalsraum, Zwei-Klassenproblem, k=5 Graphik aus Duda, Hart, Stork: Pattern Classification 2nd edition, Wiley-Interscience Vorlesung "Intelligente Systeme" 167 Nicht-parametrische Methoden K-Nächste-Nachbar-Klassifikator Vergleich mit Bayes: {( x1 , C1 ), ( x2 , C2 ),..., ( xN , CN )} Entscheidungsfehler E E Bayes E1 NN 2 E Bayes E3 NN E Bayes 3 E Bayes 2 Für k=3, großes N und kleinen Bayes-Fehler gute Approximation für Bayes. Weitere Verbesserung im Limes für größeres k. Vorteil: Kein Training erforderlich Nachteil: Komplexität hoch: Speicherbedarf O(N), Abstandsberechnung O(Dimension), Suche kleinster Abstand O(d*N2) bis O(d*N*lnN). => Effizienzsteigerung durch Verdichtung der Stichprobe Vorlesung "Intelligente Systeme" 168 Nicht-parametrische Methoden Nächste-Nachbar-Klassifikator Effizienzsteigerung durch Verdichtung der Stichprobe Kein Beitrag eines Prototypen xi zur Klassifikation, wenn seine Voronoi-Zelle nur Nachbarzellen mit seiner eigenen Klassenzugehörigkeit besitzt. Elimination überflüssiger Elemente in der Stichprobe: Falls im Voronoi-Diagramm die Nachbarzellen der Zelle von xi die gleiche Klassenzugehörigkeit wie aufweisen, kann der Prototyp xi aus der Stichprobe entfernt werden, ohne dass die Fehlerrate des NNKlassifikators verändert wird. Vorlesung "Intelligente Systeme" 169 Nicht-parametrische Methoden Nächste-Nachbar-Klassifikator Effizienzsteigerung durch Verdichtung der Stichprobe Vorlesung "Intelligente Systeme" 170 Merkmalsvorverarbeitung und -auswahl Bei der Gesichtserkennung haben wir für jede Person eine Menge an Stichprobenmustern (z.B. Grauwertbilder) mit bekannter Klassenzugehörigkeit (z.B. Name als Klassenlabel). Rechts ist ein Zweiklassenproblem (Identifikation) dargestellt. Bei der Konstruktion eines Klassifikators ist die erste Frage: Was ist die beste Menge an Merkmalen (aus Messungen im Bild zu extrahieren) um dem Klassifikator eine richtige und robuste Klassifikation zu ermöglichen? Die einfachste Wahl der direkten Verwendung der Grauwerte aller Pixel ist keine gute Wahl, da sie einen 64Kkomponentigen Merkmalsvektor für 256x256 pixel Bilder erzeugt und der Merlmalsvektor selbst bei Verschiebungen von nur einem Pixel wesentlich gedreht wird. Person P Klassifikation P nicht P Vorlesung "Intelligente Systeme" 171 Merkmalsvorverarbeitung und -auswahl Zunächst wird alles verfügbare a priori Wissen genutzt, wie z.B.: Korrigiere zuerst alle Verzerrungen, die bekannt sind oder in den Mustern selbst gemessen werden können. Eliminiere dann sämtliches Rauschen und alle Störungen, die nicht vom Objekt herrühren. Entferne Elemente aus den Mustern, die innerhalb einer Klasse stark variieren können oder instabil sind (z.B. hochfrequ. Komp. in Gesichtserkennung). Nach den obigen Filterungen und Transformationen folgt eine eventuelle Vorverarbeitung der Stichprobe mittels Entfernung von Ausreissern, Datennormierung und Substituierung fehlender Daten. Letztlich werden robuste, meßbare Merkmale mit hoher Trennbarkeit ausgewählt durch entweder • Nutzung von Modellwissen oder • Statistische Analyse Vorlesung "Intelligente Systeme" 172 Merkmalsvorverarbeitung und -auswahl Vorverarbeitung durch Entfernung von Ausreißern Ausreißer: Punkt, der weit entfernt liegt vom Mittelwert einer Zufallsvariablen. Mögliche Ursachen: • Meßfehler, p • Stichprobenwert aus dem „Außenbereich“ der Verteilung erwischt, • Stichprobe besitzt lange „Außenbereiche”. Um das Problem anzugehen, sollte eine hinreichend große xm Stichprobe vorliegen, um • statistisch signifikant Mittelwert und Standardabweichung berechnen zu können, • eine gute Schätzung der Verteilung zu ermöglichen. Für eine normalverteilte Zufallsvariable mit Standardabweichung , deckt die Fläche um 2 um den Mittelwert 95% und um 3 99% aller Punkte ab. Noch weiter entfernte Punkte sind höchstwahrscheinlich Fehlmessungen und erzeugen beim Training große Fehler. Solche Punkte sollten entfernt werden. p p Ist die Anzahl der Ausreißer nicht klein, kann dies durch eine breite Verteilungsfunktion bedingt sein. Dann gibt die Quadratfehlersummen-Kostenfunktion den außenliegenden Werten zuviel Gewicht (wegen der Quadrierung) und es sollte eine geeignetere Kostenfunktion (Kreuz-Entropie) gewählt werden. Vorlesung "Intelligente Systeme" xo x xm+2 xm xm+ xo x xm xo x 173 Merkmalsvorverarbeitung und -auswahl Vorverarbeitung durch Datennormierung Der Meßprozeß zur Extraktion von Primärmerkmalen aus den Mustern kann in sehr unterschiedlichen dynamischen Bereichen für die verschiedenen Merkmale resultieren. So kann beim Punktschweißen die Schweißspannung von 0 V bis 1 kV variieren, der Schweißstrom (bei einer Konstantstromsteuerung) lediglich von 1,8 kA bis 1,9 kA. Problem: Merkmale mit großen Werten haben mehr Einfluß auf die Kostenfunktion als Merkmale mit kleinen Werten, was nicht unbedingt ihre Signifikanz widerspiegelt. Lösung: Normierung der Merkmale derart, dass die Werte aller Merkmale in ähnlichen Bereichen liegen. Maßnahme: Normierung mit den jeweiligen Schätzwerten von Mittelwert und Varianz: Angenommen, wir haben eine Stichprobe aus N Daten des Merkmals f, dann 1 xf N 2 N x i 1 fi , f 1, 2, ..., L und f Normierung von x : xˆ fi 2 1 N x fi x f N 1 i 1 x fi x f f2 Nach der Normierung haben alle Merkmale den Mittelwert Null und Einheitsvarianz. Vorlesung "Intelligente Systeme" 174 Merkmalsvorverarbeitung und -auswahl Die obige Methode ist linear. Sind die Daten nicht gleichmäßig um den Mittelwert verteilt, sind nicht-lineare Normierungen angezeigt. Diese können logarithmische oder logistische Funktionen sein, welche die Daten in vorgegebene Intervalle abbilden. Das softmax scaling ist ein weit verbreiteter Ansatz: 1 xf N 2 N x i 1 fi , f 1, 2, ..., L und f Normierung von x : 2 1 N x fi x f N 1 i 1 1 xˆ fi 1 e x fi x f r f 2 Dies begrenzt den Bereich auf das Intervall [0,1]. Für kleine Werte des Arguments ergibt sich wieder eine lineare Methode. Der Grad der nicht-linearen Stauchung hängt vom Wert von und vom Parameter r ab. Vorlesung "Intelligente Systeme" 175 Merkmalsvorverarbeitung und -auswahl Vorverarbeitung durch Ergänzung fehlender Daten Problem: Manchmal ist die Anzahl verfügbarer Daten nicht für alle Merkmale gleich (z.B. asynchrone Messungen unterschiedlicher Frequenz). Für das Training wird jedoch die gleiche Anzahl von Daten für alle Merkmale benötigt. Lösung: •Wenn wir über viele Trainingsdaten verfügen und nur einige Messungen von Merkmalswerten fehlen, können Merkmalsvektoren mit fehlenden Elementen aus dem Trainingsdatensatz herausgenommen werden. •Wenn wir uns den Luxus des Wegwerfens von Merkmalsvektoren nicht leisten können, müssen wir die fehlenden Werte durch Schätzwerte ersetzen: • Mittelwert der verfügbaren Merkmalswerte, • Interpolationswert zwischen Vorgänger und Nachfolger • Schätzwert aus der zugrundeliegenden Verteilung (wenn verfügbar) Vorlesung "Intelligente Systeme" 176 Merkmalsvorverarbeitung und -auswahl Bewertung und Auswahl von Merkmalen 1. Einzelmerkmale Um einen ersten Eindruck von den ausgewählten Merkmalen zu erhalten, ist es nützlich, die Trennfähigkeit eines jeden einzelnen Merkmals zu betrachten. Dieses Vorgehen filtert Merkmale heraus, die keine Information über Klassenzugehörigkeiten enthalten. 2. Merkmalskombination Danach ist die beste Kombination der übrig gebliebenen Merkmale zu einem Merkmalsvektor zu betrachten. Vorlesung "Intelligente Systeme" 177 Merkmalsvorverarbeitung und -auswahl Einzelmerkmals-Auswahl: t-Test für die Merkmalsauswahl Angenommen, wir haben ein Zweiklassenproblem und es sei das betrachtete Merkmal eine Zufallsvariable, dann lautet die Aufgabe, die folgenden Hypothesen zu testen: H1: Die Merkmalswerte unterscheiden sich nicht wesentlich für unterschiedliche Klassen. H0: Die Merkmalswerte unterscheiden sich wesentlich für unterschiedliche Klassen. H0 ist dabei die Nullhypothese und H1 die Alternativhypothese. Angenommen, Merkmal x gehört zu einer bekannten Familie von Wahrscheinlichkeitsverteilungsfunktionen mit einem unbekannten Parameter µ. Im Falle Gaußscher Verteilungen kann µ der Mittelwert oder die Varianz sein. Wenn bekannt ist, daß die Varianz denselben Wert hat, lautet die Frage, ob sich die Mittelwerte µ1 und µ2 des Merkmals x für die beiden Klassen wesentlich unterscheiden. H1: Dµ = µ1 - µ2 0, H0: Dµ = µ1 - µ2 = 0 Werden die Werte von x für die Klasse 1 mit X und für Klasse 2 mit Y bezeichnet, definieren wir Z=X-Y. Dann können wir die Stichprobe für z verwenden, um auf die Dµ Hypothese hin zu testen und einen t-Test durchführen mit 1 Z N N X i 1 i Yi X Y Vorlesung "Intelligente Systeme" 178 Merkmalsvorverarbeitung und -auswahl Klassentrennbarkeit : Receiver operating characteristics Kurve Prüfung bislang auf wesentlichen Unterschied der Mittelwerte eines Merkmals zweier Klassen: Merkmale mit ungefähr gleichem Mittelwert werden ausgeschlossen. Maß für Unterscheidungsfähigkeit eines Merkmals: ROC (Zusätzliche Betrachtung des Überlapps der Wahrscheinlichkeitsverteilungsfunktionen für die beiden Klassen). Wir können einen Schwellwert zwischen beiden Klassen definieren: Schwellwert p p Klasse1 Klasse2 Klasse2 Klasse1 Xm Ym x 1 b 1b x Wahrscheinlichkeit einer falschen Entscheidung über die Klasse1-Zugehörigkeit: Fläche unter der oberen Kurve rechts vom Schwellwert; Wahrscheinlichkeit einer korrekten Entscheidung 1- . Entsprechend für Klasse2: b und 1-b. Die Variation des Schwellwerts ergibt die ROC Kurve: 1-b Bei vollständigem Überlapp ist 1-b (Diagonale), ohne Überlapp 1 ist 1-b = 1 unabhängig von , ansonsten erhalten wir eine Kurve wie im Diagramm. Die Fläche zwischen dieser Kurve und der DiaA gonale ist ein Überlapp-Maß zwischen 0 und 0,5. Die ROC Kurve: Durchfahren des Wertebereichs von x mit dem Schwellwert und Berechnung und Auftragung von 1 = 1-b im Diagramm. 179 Vorlesung "Intelligente Systeme" Merkmalsvorverarbeitung und -auswahl Merkmalsvektor-Klassentrennbarkeitsmaße Die bisherigen Betrachtungen sind nicht geeignet, die Korrelationen zwischen Merkmalen zu berücksichtigen, die üblicherweise bestehen und die Unterscheidungseffizienz eines Merkmalsvektors beeinflussen. 1. Divergenz Gegeben seien zwei Klassen c1 und c2. Gemäß der Bayes´schen Regel wird ein Merkmalsvektor x zugeordnet zu c1 wenn P(c1|x) > P(c2|x). Unterscheidbarkeit für eine Merkmalsausprägung d=ln[p(c1|x)/p(c2|x)]. Mittelwerte von d: p ( x | c1) p ( x | c 2) D12 p ( x | c1) ln dx und D21 p ( x | c 2) ln dx p ( x | c 2 ) p ( x | c 1 ) Symmetrische Kombination: Divergenz d p ( x | c1) d12 p ( x | c1) p ( x | c 2) ln dx p ( x | c 2) Vorlesung "Intelligente Systeme" 180 Merkmalsvorverarbeitung und -auswahl Merkmalsvektor-Klassentrennbarkeitsmaße Divergenz bei Normalverteilungen p ( x | c1) d12 p ( x | c1) p ( x | c 2) ln dx p ( x | c 2 ) Für mehrdimensionale Gaussfunktionen mit Mittelwertvektoren und Kovarianzmartizen S p( x ) 12 12 21 22 S k1 12 1 e 2 S 1k 2k k2 1 T 1 x S x 2 ij E[( xi i ) ( x j j )], i2 E[( xi i ) 2 ] Vorlesung "Intelligente Systeme" 181 Merkmalsvorverarbeitung und -auswahl p ( x ) Mit 1 e 2 S dann gleich d12 1 T 1 x S x 2 1 spur 2 1 1 p ( x | c1) ist Divergenz d12 p ( x | c1) p ( x | c 2) ln dx p ( x | c 2 ) 2 1 2 1 1 2 I ( 1 2 )T 2 1 1 2 1 ( ) 1 was sich im eindimensionalen Fall reduziert zu 1 1 1 22 12 1 d12 2 2 2 ( 1 2 ) 2 2 2 2 1 2 2 1 2 Verallgemeinerung auf Mehrklassen-Trennbarkeitsmaß M: Anzahl der Klassen M M d P(wi ) P(w j )dij i 1 j 1 Vorlesung "Intelligente Systeme" 182 2 Merkmalsvorverarbeitung und -auswahl 2. Fishers discriminant ratio Das FDR Maß basiert auf der sogenannten Streumatrix-Methode. Für Zweiklassenprobleme in einer Dimension (ein Merkmal) hat die FDR folgende Form: 1 2 2 FDR 12 22 Für Mehrklassenprobleme können mittelnde Formen der FDR benutzt werden: M FDR i 1 M j i i j 2 i2 2j wobei die Indizes i und j sich auf Mittelwert und Varianz (des betrachteten Merkmals) für die Klassen ci und cj beziehen. 3. Weitere Klassentrennbarkeitsmaße Chernoff Rand und Brattcharrya Distanz. Die Mahalanobis-Distanz ist ein Spezialfall von (1.), wobei die Wahrscheinlichkeitsverteilungsfunktionen gleiche Kovarianzmatrizen besitzen. Vorlesung "Intelligente Systeme" 183 Merkmalsvorverarbeitung und -auswahl 4. Visualisierung des Merkmalsraumes mit entsprechenden Werkzeugen http://quickcog.phytec.de/ Vorlesung "Intelligente Systeme" 184 Merkmalsauswahl Merkmalsvektorauswahl Um den optimalen Merkmalsvektor aufzufinden, könnten wir eine vollständige Suche unter allen Kombinationen von l Merkmalen aus m möglichen durchführen. Wir würden die beste Kombination bezüglich eines bestimmten Trennbarkeitsmaßes suchen. Für große Werte von m kann dies ein ernsthaftes kombinatorisches Problem werden, da m m! Gesamtzahl möglicher Vektoren : l l!(m l )! Beispiel: vollständige Suche nach Kombination der 5 besten Merkmale von 20 ergibt 15504 zu untersuchende Kombinationen. Aus diesem Grund gibt es viele Suchtechniken wie - Sequential forward selection 1. Bestes Einzelmerkmal M1 2. Beste Kombination von M1 mit einem weiteren Merkmal: M1,M2 3. Beste Kombination von M1,M2 mit einem weiteren Merkmal: M1,M2,M3 … bis gewünschte Leistung erreicht ist. Anzahl zu untersuchender Kombinationen: l+(l-1)+(l-2)+…+(l-m-1). - Genetische Algorithmen Vorlesung "Intelligente Systeme" 185 Merkmalsauswahl Merkmalserzeugung Merkmale können rohe Meßwerte der zugrundeliegenden Muster sein. Dies kann zu sehr hochdimensionalen Merkmalsvektoren führen mit stark korrelierten Merkmalen und folgedessen Redundanz der Information. Die Aufgabe der Merkmalserzeugung ist die Beseitigung dieser Redundanzen durch Transformationen der rohen Meßwerte auf neue Koordinaten und die Auswahl nur solcher Koordinaten als neue Merkmale, die den höchsten Grad an Information beinhalten. Dies sollte zu einer Kompression der klassifikationsrelevanten Information in eine relativ kleine Anzahl von Merkmalen führen. Z.B. genügt bei der Gesichtserkennung eine Transformation auf ein System aus 50 „Eigengesichtern“ um alle Gesichter mit ausreichender Genauigkeit zu beschreiben, während die Ursprungsbilder aus z.B. 65536 Werten bestehen. Lineare Transformationen Karhunen-Loève (Eigenvektor-Zerlegung) Singulärwertzerlegung Fourier-Transformation Hadamard Transformation Wavelet Transformation ... Signaleigenschaften Invariante Momente, Textur, Rauhigkeit,.... Anwendungsbeispiel Qualitätskontrolle beim Widerstands-Punktschweißen Inkl. Merkmalserzeugung und Merkmalsauswahl Vorlesung "Intelligente Systeme" 186 Zwei ursprüngliche Merkmale x1 und x2 sind der Stichprobenverteilung nicht gut angepasst. Besser x1´ und x2´ : Zur Beschreibung genügt x1´: Linearer Unterraum von x1, x2. h x2 Hauptkomponenten-Transformation x1 h Vorlesung "Intelligente Systeme" 187 x2 Hauptkomponenten-Transformation 2. Drehung auf Richtung maximaler Varianz h 1. Verschiebung in den Schwerpunkt x1 h Vorlesung "Intelligente Systeme" 188 x2 Hauptkomponenten-Transformation 7.1 8 9.2 9.9 10.9 11.8 13.1 x6 , x7 , x8 , x9 , x10 , x11, x12 , , , , , , 6.9 8.1 8.9 10.2 11 11.9 13 14,00 12,00 10,00 8,00 6,00 1 91 7.6 xS 12 91 7.6 4,00 h 2,00 1.1 2 3.2 3.9 4.8 x1 , x2 , x3 , x4 , x5 , , , , 0.9 2.1 2.9 4 5.1 0,00 0,00 5,00 10,00 15,00 x1 h Vorlesung "Intelligente Systeme" 189 Hauptkomponenten-Transformation 1. Allgemeines Vorgehen Muster-Stichprobe Schätzung Schwerpunkt X [x1 ,..., xN ] x i R m y i : x i x s y i Rm 1 N xs xi N i 1 Y [y1 ,..., yN ] Y R m N Empirische Kovarianz-Matrix K 1 1 N T T Y Y yi yi N 1 N 1 i 1 K R m m Hauptachsen a i und Hauptachsenabschnitte l i | a K ai li ai i | 1 durch Diagonalisierung von K und davon Eigenwerte, Eigenvektoren Vorlesung "Intelligente Systeme" 190 x2 Hauptkomponenten-Transformation 7.1 8 9.2 9.9 10.9 11.8 13.1 x6 , x7 , x8 , x9 , x10 , x11, x12 , , , , , , 6.9 8.1 8.9 10.2 11 11.9 13 14,00 Muster-Stichprobe 12,00 10,00 8,00 1.1 2 3.2 3.9 4.8 x1 , x2 , x3 , x4 , x5 , , , , 6,00 .9 2.1 2.9 4 5.1 0 1 91 7.6 xS 12 91 7.6 4,00 h 2,00 Y x1 xS 0,00 x x ... 0,00 2 S y i : x i x s Schätzung Schwerpunkt 1 xs N N x i 1 y i R m Y [y1 ,..., yN ] 6.5 5.6 4.4 3.7 2.8 0.5 0.4 1.6 2.3 3.3 4.2 5.5 x1 x12 xS 5.5 4.7 3.6 10,00 2.5 0.7 0.5 1.3 15,00 2.6 3.4 4.3 5.4 6.75,00 Empirische Kovarianz-Matrix h 1 181.54 182.94 16.5 16.63 K Y Y T 11 182.94 184.84 16.63 16.8 Vorlesung "Intelligente Systeme" 191 i x2 Hauptkomponenten-Transformation Empirische Kovarianz-Matrix 1 181.54 182.94 16.5 16.63 K Y Y T 11 182.94 184.84 16.63 16.8 Hauptachsen a i und Hauptachsenabschnitte li K ai li ai 14,00 1. Charakteristisches Polynom null setzen: Nullstellen sind gesuchte Eigenwerte. 12,00 1 0 0 0 1 10,00 ln a1ln 1 a2 ln 2 ... an 0 det K l I 0, I 0 8,00 0 0 1 6,00 .5 l 16.63 ! 16 16.5 16.8 det 0 l1, 2 2 16.63 16.8 l 4,00 16.5 16.82 16.632 l 1 4 0.019, l2 33.28 h 2. Eigenvektoren durch Einsetzen in und Lösen von 2,00 0.71 0.7 K 0,00 li I ai 0 a1 , a2 0.7 0.71 0,00 5,00 10,00 Vorlesung "Intelligente Systeme" 15,00 x1 192 Hauptkomponenten-Transformation X [x1 ,..., xN ] x i R m y i R m Y [y1 ,..., yN ] Y R m N y i : x i x s 2. Singulärwert-Zerlegung SVD von Y r Ys si u i v Ti i 1 r s1 s2 ... sr 0 u i , v i orthonormiert , u i R m , v i R N Ys T si v i u Ti i 1 r Ys Ys s2i u i u Ti Ys Ys T R m m T i 1 Y Y T T s s s2i 2 Ys Ys Ys Ys u i si u i l i , a i ui N 1 T T 3. Eigenwert-Zerlegung von Y T Y Y T Y s2i v i v Ti Y T Y v i s2i v i R N N Yv 1 Y v i s i u i s i a i a i Yv i i si | Yv i | ! Vorlesung "Intelligente Systeme" 193 Hauptkomponenten-Transformation X [x1 ,..., xN ] x i R m y i : x i x s y i R m Y [y1 ,..., yN ] Y R m N 4. Vorgehen zur Lösung der PCA 1. X xs Y EW 1 2. I) K YY T N 1 SVD m N II) Y EW N N III) Y T Y si , u i , v i m m li , a i s2i li , ai ui N 1 Y TY vi i vi i ! Y vi li , ai N 1 |Y vi | wenn N > m, dann I), wenn N < m, dann III) Bemerkung: Y T Y i , j y i y j Vorlesung "Intelligente Systeme" 194 Jede m x n – Matrix A mit m > n kann geschrieben werden als Produkt einer m x m, spalten-normalen Matrix U, einer positiv semi-definiten n x n Diagonalmatrix W und der Transponierten einer n x n normalen Matrix V. w1 0 . 0 T 0 w2 . 0 T T T A U W V mit W , w1 , w2 ,..., wn 0 und U U V V VV I . . . . 0 0 . w n Vorlesung "Intelligente Systeme" 195 Hauptkomponenten-Transformation 5. Beispiel: Eigengesichter Hauptachsen a i und Hauptachsenabschnitte l i • Sortieren nach Hauptachsenabschnitten (relative Relevanz) • Abschneiden ab Schwellwert • Zugehörige Eigenvektoren: Hauptkomponenten (neue Basis) 1 xs N a1 N x i 1 a2 i “Durchschnittsgesicht” a1 , a2 ,... “Eigengesichter” Vorlesung "Intelligente Systeme" 196 Hauptkomponenten-Transformation Merkmalsgewinnung: • Subtraktion des Schwerpunkts vom Eingangsmuster • Projektion des Ergebnisses auf die Hauptkomponenten x x xs c1 x a1 , c2 x a2 , , cN x a N x c1 a1 c2 a2 cN a N xs Vorlesung "Intelligente Systeme" 197 Einbringen von a priori Wissen Klassenzugehörigkeit |1|0|0| |1|5|7|8|3|4| Bisher: Erlernen einer Abbildung Muster Anhand einer bekannten Stichprobe Muster 1 Muster N . : Klassenzugehörigkeit 1 Klassenzugehörigkeit N Jetzt: Nutzung von a priori Wissen a) Nur bestimmte zeitliche Abfolgen sind möglich Zeitdiskrete Prozesse: Hidden-Markov-Modelle b) Kausale Zusammenhänge sind bekannt oder vermutet: Bayesian Belief Networks c) Randbedingungen für die Lösung sind bekannt: KostenfunktionRegularisierung Vorlesung "Intelligente Systeme" 198 Digitale Signale: ADC und DAC Mustererkennungssystem Beobachtbare Prozessmuster Sensor/ Wandler Signalaufbereitung Klassifik. A D Merkmal-/ Primitiveextraktion Estimation Deskription Mögl. Algorithmenrückkopplung oder -interaktion Analoge Welt • Diskrete Abtastung • Quantisierung Vorlesung "Intelligente Systeme" Digitale Welt 199 Fehlerquellen bei der Analog-Digital-Wandlung • Diskrete Abtastung • Quantisierung Analoge Welt Analoger Eingang ADCAnalog/ Digital Converter Sample & Hold Digitaler Ausgang Wandeln des Signals zur nächsten Ganzzahl Abgetastetes Analogsignal Ursprüngl. Analogsignal Digitalisiertes Signal Digitale Zahl Amplitude (phys. Einh.) Amplitude (phys. Einh.) Einfrieren der Werte an Abtastzeitpunkten Zeit Digitale Welt Zeit Vorlesung "Intelligente Systeme" Abtastpunkt 200 Fehlerquellen bei der Analog-Digital-Wandlung ADCAnalog/ Digital Converter Fehlerquelle Quantisierungsfehler Digitaler Ausgang Wandeln des Signals zur nächsten Ganzzahl Abgetastetes Analogsignal Digitale Zahl Digitalisiertes Signal Zeit Abtastpunkt Differenz zw. abget. Analogsignal und digit. Signal Fehler (in LSBs) Quantisierungsfehler Abtastpunkt Vorlesung "Intelligente Systeme" 201 Fehlerquellen bei der Analog-Digital-Wandlung Fehlerquelle Aliasing Graphiken aus Steven W. Smith „The Scientist and Engineer´s Guide to Figital Signal Processing“ Abtastung mit mindestens der doppelten Schwingungsfrequenz Vorlesung "Intelligente Systeme" 202 Frequenzraumdarstellung Ortsraum - Frequenzraum Signale können als Überlagerung (Summe) periodischer Funktionen mit Frequenzen w und mit Amplituden F dargestellt werden: y(x) Applet Cosinus Funktionen Transformation in Frequenzraum N 1 y ( x) Fe (k ) coswk x Fo (k ) sin wk x ; wk k k 0 Sinus Funktionen 2 N 2 2 Fe (k ) cos k x Fo (k ) sin k x N N k 0 N 1 Diskrete Fourier-(Rück)Transformation Frequenzraum-Darstellung gibt an, mit welcher Häufigkeit jeweils periodische Funktionen vorkommen. Vorlesung "Intelligente Systeme" 203 Frequenzraumdarstellung 1 Fe (k ) N Fe (k ) 1 N N 1 1 y ( x ) cos w x ; F ( k ) k o N x 0 2k y ( x ) cos N x 0 N 1 N 1 y( x) sin wk x ; wk x 0 1 x ; Fo (k ) N 2k y ( x ) sin N x 0 N 1 Nach einer Bearbeitung im Frequenzraum Fe(k)→Fe~(k) und Fo(k)→Fo~(k) N 1 in den Ortsraum zurück transformiert werden. kann wieder 2 ~ ~ k 0 2 ~ Fe (k ) cos k N k 0 N 1 2 ~ x Fo (k ) sin k N x Vorlesung "Intelligente Systeme" Ortsraum Frequenzraum Signal y im Ortsraum, Abtastwerte y(i) Im Frequenzraum sind viele Operationen günstiger. Alle linearen Operationen z.B. Hochpass, Tiefpass, Bandpass und Bandsperre mit hoher Güte Erkennung periodischer Strukturen Manipulation periodischer Strukturen ~ y ( x) Fe (k ) coswk x Fo (k ) sin wk x ; wk k x 2k Analyse: N Transformation N Synthese: Transformation Frequenzraum Ortsraum 204 Frequenzraumdarstellung Polare Notation – komplexe Schreibweise N 1 1 Fe (k ) N 1 y ( x ) cos w x ; F ( k ) k o N x 0 1 Fe (k ) N 2k y ( x ) cos N x 0 F(k) Fo(k) F Fe(k) N 1 F (k ) F (k ) e 2 y( x) sin wk x ; wk x 0 1 x ; Fo (k ) N Fo (k ) 2 ; Phase Komplexe Schreibweise N 1 y ( x )e x 0 2k y ( x ) sin N x 0 N 1 Amplitude, Betrag (Magnitude) Fo (k ) f (k ) arctan Fe (k ) 1 F (k ) N N 1 2k N x Fe (k ) F (k ) cos[f (k )] Fo (k ) F (k ) sin[ f (k )] F (k ) F (k ) eif ( k ) iw k x 2k ; wk ; N Vorlesung "Intelligente Systeme" N 1 y ( x ) F ( k ) e iw k x x 0 205 Frequenzraumdarstellung Operationen im Frequenzraum Filterung der abgetasteten Funktion y: Analyse N 1 N 1 1 Fe (k ) N 1 y ( x ) cos w x ; F ( k ) k o N x 0 y( x) sin wk x ; wk 1 Fe (k ) N 1 2k y ( x ) cos x ; F ( k ) o N N x 0 x 0 N 1 2k N 2k y ( x ) sin x N x 0 N 1 Multiplikation mit Filterfunktion Filterfunktion, Abtastwerte f(k) Synthese ~ Fe (k ) f (k ) Fe (k ) ~ Fo (k ) f (k ) Fo (k ) 2 ~ ~ ~ y ( x) Fe (k ) coswk x Fo (k ) sin wk x ; wk k N k 0 N 1 2 2 ~ ~ Fe (k ) cos k x Fo (k ) sin k x N N k 0 N 1 Vorlesung "Intelligente Systeme" 206 Literatur R. O. Duda, P. E. Hart, D. G. Stork: Pattern Classification, 2nd ed., Wiley, New York 2001 C. M. Bishop: Pattern Recognition and Machine Learning, Springer, Berlin 2004 Weitere Literaturangaben unter http://www.iwi.hs-karlsruhe.de/~lino0001 /BeschrIntelliSys.htm Vorlesung "Intelligente Systeme" 207 Lineare Trennung nach nichtlinearer Transformation Vorlesung "Intelligente Systeme" 208 Kostenfunktion (Anzahl Fehler) Vorlesung "Intelligente Systeme" 209 Kostenfunktion (Perzeptron) Vorlesung "Intelligente Systeme" 210 Kostenfunktion (quadratisch) Vorlesung "Intelligente Systeme" 211 2-Klassenproblem Vorlesung "Intelligente Systeme" 212 3-Klassenproblem Vorlesung "Intelligente Systeme" 213 Perzeptronalgorithmus Vorlesung "Intelligente Systeme" 214 Perzeptronalgorithmus Vorlesung "Intelligente Systeme" 215 Perzeptronalgorithmus Vorlesung "Intelligente Systeme" 216 Perzeptronalgorithmus Vorlesung "Intelligente Systeme" 217 Lineare SVM Vorlesung "Intelligente Systeme" 218 Lineare SVM Vorlesung "Intelligente Systeme" 219 Lineare SVM Vorlesung "Intelligente Systeme" 220 Lineare SVM Vorlesung "Intelligente Systeme" 221 Funktionsapproximation durch Neuronales Netz Vorlesung "Intelligente Systeme" 222 K-Nächste-Nachbar-Klassifikator p( x0 | ci ) : Bestimmung der klassenbed ingte Wahrschein lichkeitsd ichte für ein Muster x0 durch Betrachtun g einer Nachbarsch aft R um x mit Volumen V . Annahme : Konstante Verteilung sdichte innerhalb R. P( x R | ci ) p( x | ci ) dx p( x0 | ci ) dx p( x0 | ci )V R R Stichprobe mit Umfang N i für Klasse ci , davon ni Stichprobe n innerhalb R. Vorlesung "Intelligente Systeme" 223 K-Nächste-Nachbar-Klassifikator N i i N, Ni P(ci ) , N ni p ( x0 | ci ) V Ni ni N i ni p ( x0 | ci ) P(ci ) V Ni N V N ni k i p( x0 | ci ) P(ci ) i V N V N p ( x0 | ci ) P (ci ) Bayes : P(ci | x0 ) p( x0 | ci ) P(ci ) (k NN) i ni V N ni VN k k Vorlesung "Intelligente Systeme" 224 K-Nächste-Nachbar-Klassifikator Für die Anwendung des NN bzw. k - NN Klassifika tors ist ein Abstandsma ß notwendig. Definition : Eine Distanzfun ktion d ( x, y ) heißt Metrik genau dann, wenn 1. d ( x, y ) 0 2. d ( x , y ) d ( y , x ) 3. d ( x, y ) 0 x y 4. d ( x, y ) d ( y, z ) d ( x, z ) (Dreiecksu ngleichung ) Eigenschaf t : Für eine Metrik gilt d ( x, y ) d ( y, z ) d ( x, z ) Vorlesung "Intelligente Systeme" 225 K-Nächste-Nachbar-Klassifikator Beispiel : Minkowski - Metriken in n (auch Lk Norm genannt) n k Lk ( x , y ) xi yi i 1 1 k n L1 xi yi Cityblock oder Manhattan Metrik L2 ( x y ) t ( x y ) Euklidisch e Distanz i 1 L max xi yi , 1 i n Chebychev Distanz Vorsicht bei Skalierung im Merkmalsra um! Vorlesung "Intelligente Systeme" 226 K-Nächste-Nachbar-Klassifikator Vorlesung "Intelligente Systeme" 227