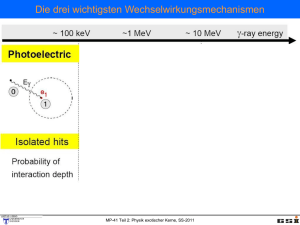
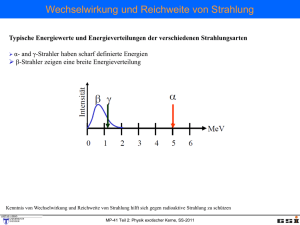
235 U

MP-41 Teil 2: Physik exotischer Kerne
13.4.
20.4.
27.4.
4.5.
11.5.
18.5.
25.5.
1.6.
8.6.
15.6.
22.6.
29.6.
6.7.
13.7.
Einführung, Beschleuniger
Schwerionenreaktionen, Synthese superschwerer Kerne (SHE)
Kernspaltung und Produktion neutronenreicher Kerne
Fragmentation zur Erzeugung exotischer Kerne
Halo-Kerne, gebundener Betazerfall, 2-Protonenzerfall
Wechselwirkung mit Materie, Detektoren
Schalenmodell, Restwechselwirkung
Restwechselwirkung, Seniority
Tutorium-1
Tutorium-2
Vibrator, Rotator, Symmetrien
Schalenstruktur fernab der Stabilität
Tutorium-3
Klausur
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Entdeckung der Kernspaltung und Kettenreaktion
1932
Entdeckung des Kernbausteins Neutron durch Chadwick
( 4He + 9Be → 12C + 1n + γ)
(Nobelpreis 1935)
1933
Fermi beschießt systematisch Kerne mit moderierten
Neutronen, entdeckt induzierte Radioaktivität
(Nobelpreis 1938 und Emigration)
Enrico Fermi (1901-1954)
Theoretiker und Experimentator
Fermistatistik, schwache Wechselwirkung,
erster Kernreaktor
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Entdeckung der Kernspaltung und Kettenreaktion
1938
Nachweis der Kernspaltung durch Hahn, Meitner, Strassmann über chemischen Nachweis
von Barium (Nobelpreis 1944 ohne L.M.)
Otto Hahn (1879-1968)
Lise Meitner (1878-1968)
(Emigration 1938)
Fritz Strassmann (1902-1980)
1939
Nachweis von Spaltungsneutronen, damit Potential zur Kettenreaktion bewiesen
(Szilard sah dies 1933 voraus)
1942
Beginn des Manhatten Projektes, Initiator Szilard
(Brief 1939 von Szilard, Einstein, Wigner an Roosevelt
1942
Fermi baut Kernreaktor und erreicht erste kontrollierte Kernspaltung
1945
Atombomben (Spaltung von U-235 und Pu-239) über Hiroshima und Nagasaki
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Uran-Zerfall
 Eine Supernova-Explosion vor knapp 6 Milliarden Jahren hat die Isotope
Uran-238 (T1/2 =4,5109 Jahre), Uran-235 (T1/2 =0,7109 Jahre) und
Plutonium-239 (T1/2 =24103 Jahre) zu etwa gleichen Anteilen erzeugt.
Pu-239 war bald zerfallen, vom U-235 sind heute 0,3 % und vom U-238
sind 40 % übrig geblieben. Uran-Brennelemente erfordern eine U-235
Anreicherung auf mindestens 3 %.
 Gute Gesteinslagerstätten enthalten 0,3 % Uran und werden mit ca.
$50/kg Uran gefördert, die Weltreserven liegen bei 10 Mio Tonnen
Natururan. Weitere 100 106 t werden im Gestein mit Abbaukosten bis
$300/kg vermutet. Sicher sind 4,2 109 t Natururan im Meerwasser mit
Gewinnungskosten von $500/kg.
 Alpha-Zerfall:
U 
238
92
Th  
234
90
 Spontane Spaltung:
- Zerfall der natürlich vorkommenden Uranisotope
U 
140
54
U 
142
56
238
92
235
92
Xe 
96
38
Sr  2 01n
Ba 
90
36
Kr  3 01n
Uran ist ein silberweiß glänzendes,
weiches Schwermetall
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Wiederholung: Energiebilanz
e) Energiebilanz der
235
92
U -Spaltung
Kernbindungsenergie pro Nukleon
als Funktion der Zahl A von Nukleonen
 Eisen (A=60) und Nachbarn sind am stärksten gebunden
Daraus folgt:
 Energie wird frei bei Fusion von leichten Kernen zu schwereren Kernen bis hin zum Eisen. (Sonne)
 Energie wird frei bei Zerfall und Spaltung von schweren Kernen in Bruchstücke.
Kernenergie ist also analog zu der chemischen Energie: Energie wird frei beim
Übergang in einen Zustand mit stärkerer Bindung der Kernbausteine.
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Energiegewinn für 235-U
Energiebilanz der
235
92
U -Spaltung
Mass data: nucleardata.nuclear.lu.se/database/masses/
Mass (1u=931.478MeV/c2):
236.045562u → 88.917633u + 143.922940u + 3.025995u
Energiegewinn: 166.73MeV
Binding energy [M(A,Z) - Z·M(1H) - N·M(1n)] :
-1790.415MeV → -766.908MeV - 1190.239MeV
Energiegewinn: 166.73MeV
1g Uran → Spaltprodukte
Mass excess [M(A,Z) - A] :
42.441MeV → -76.725MeV – 71.780MeV + 24.214MeV
Energiegewinn: 166.73MeV
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
68 Millionen kJ
Spontane Kernspaltung
Spaltung wird bei schweren Kernen
durch die zunehmende Coulomb-Kraft
zwischen den Protonen verursacht.
R
VC 
R/21/3
2·R/21/3
Z 2  e2
Z2

0
.
189

1/ 3
A1/ 3
8  1 / 2   r0  A1/ 3
Eexp
MeV 
Z2
 0.1071 1/ 3  22.2
A
MeV 
Spaltfragmente sind deformiert
Durch die ellipsoidförmige Deformation
während der Spaltung ändern sich die
Oberflächenenergie und die Coulombenergie.
Durch Betrachtungen der beiden
Energieterme erhält man, dass Kerne, für die
Z2/A ≥ 51 erfüllt ist, spontan spalten.
aC Z 2
1 EC
Xs  


1
2 ES 2  aS A
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Spontane Kernspaltung
Spaltbarriere:
EF  ECoul  E0
liquid drop model:
EF 0.38  0.75   S 

ES0 0.83  1   S  3
1/ 3  S  2 / 3
2 / 3 S  1
2

 N  Z   2/3
E  17.9439  1  1.7826  
  A
 A  

0
S
Z2
E  0.7053  1/ 3
A
0
C
Xs 
1 EC0

2 ES0
MeV 
MeV 
das Verhältnis spielt eine entscheidende Rolle
Cohen, Plasil, Swiatecki, Ann. of Phys. 82 (1974), 557
Z2/A
ES0
EC0
[MeV]
[MeV]
XS
ΔEF
[MeV]
235U
36.02
626.0
967.4
0.773
6.1
238U
35.56
625.9
963.3
0.770
6.4
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Energiebarriere für die spontane Kernspaltung
Bei Kernen mit Z2/A < 51 muss man
eine Energie ΔEF zuführen, um die
Spaltung zu erreichen. Jedoch ist auch
hier noch eine Spaltung durch
Tunneleffekt möglich.
Die Tunnelwahrscheinlichkeit nimmt mit
sinkenden Werten von Z2/A jedoch sehr
stark ab, da die Bruchstücke
vergleichsweise große Massen haben.
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Energie
Doppelte Spaltbarriere
240Pu
prompte Spaltung
238U(α,2n)240fPu,
1.
2.
Eα=25 MeV
Messung von Konversionselektronen
t1/2=3.8ns
verzögerte Spaltung
2
 3.34 keV
2
(Achsenverhältnis 2:1)
Superdeformation
2:1
Deformation
Hyperdeformation
3:1
Oblate superdeformation
1:2
Oktupole Y31
Oktupole Y30
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Induzierte Kernspaltung
Neutronen müssen keine Coulombbarriere
überwinden, so dass auch langsame Neutronen
eine Kernspaltung bewirken können.
U  n 
238
92
239
92
U*
Compound-Kern: g-u
Qfission= [M (238U) + M(1n) – M(239U) ]·c2
= 4.8 MeV
Anregungsenergie relativ klein Qfission < ΔEF = 6.4 MeV
Spaltung nicht einfach möglich
U  n 
235
92
236
92
U*
Compound-Kern: g-g
Qfission= [M (235U) + M(1n) – M(236U) ]·c2
= 6.5 MeV
Anregungsenergie relativ groß Qfission > ΔEF = 6.1 MeV
Spaltung einfach möglich
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Charakteristische Eigenschaften der Kernspaltung
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Charakteristische Eigenschaften der Kernspaltung
a) Spaltung asymmetrisch  Vielzahl hochangeregter Tochterkerne
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Charakteristische Eigenschaften der Kernspaltung
a) Spaltung asymmetrisch  Vielzahl hochangeregter Tochterkerne
b) Neutronenüberschuss in Töchtern:
Z
Z

A U A A 100
 viele -instabile Tochterkerne (oft langlebig)
Beispiele:
140
54
99
41
16 s
Xe 
2, 4 min
Nb

140
55
66 s
Cs 
99
42
140
56
67 a
Mo 
12,8 d
Ba
99
43

2105 a
Tc

140
57
40 a
La
99
44

140
58
Ce (stabil)
Ru (stabil)
 1000 verschiedene -instabile Kerne nach Spaltung
 langlebige -Strahler zusammen mit 239Pu heißen radioaktiver Müll
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Charakteristische Eigenschaften der Kernspaltung
c) Bruchstücke hochangeregt & Neutronenüberschuss
 prompte ( t < 1016s ) Neutronen-Emission
Beispiele:
n thermisch  235
 Y1  Y2  ν n  n
92 U
ν n  2,42
n thermisch  239
 Y1  Y2  ν n  n
94 Pu
ν n  2,87
Neutronen-Energiespektrum 
Abdampfen von bewegter Quelle
Maxwell-Boltzmann Verteilung
dN
 E 
~ E  exp  

dE
 k T 
k = 8.617·10-5 eV/0K
k·T0 = 0.0253 eV for T0=293.61 0K
Wichtig:
Etwa 99% der Neutronen werden sofort frei
Etwa 1% wird verzögert in der Zeitspanne
0.05s < t < 60s abgegeben
→ Regelung von Kernkraftwerken
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
E  2 MeV
Charakteristische Eigenschaften der Kernspaltung
d) Verzögerte Neutronen ( t  0,2 s  60 s )
Kern1
-Zerfall
t½  Verzögerung
Kern2  Kern 3  n
 ca. 1% der Neutronen sind verzögert
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Charakteristische Eigenschaften der Kernspaltung
e) Energiebilanz der
235
92
U -Spaltung
YKlein
100 MeV
 (Spaltkerne)
8 MeV
YGroß
70 MeV
 (Spaltkerne)
7 MeV
 nn
5 MeV
Neutrinos ( e )
12 MeV
 (prompt)
7 MeV
gesamt:
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
210 MeV
Charakteristische Eigenschaften der Kernspaltung
f)
Ternäre Spaltung in ca. 1% der Fälle:
n  Kern  Y1  Y2  leichter Kern
 H,
 symmetrisch
3
1
4
2

He , 
 große Strahlenbelastung durch Tritium
3
1
H 
3
2
E kin,e  18,6 keV
He  e   ν e
τ  12,3 a
g) Spaltquerschnitte:
σ tot E n   σ tot n  235U 
alle Prozesse
σ f E n   σn  235U 
nur Spaltung
Reaktor funktioniert  f  tot  1
235U:
f  tot  1 für En  0
( thermische Neutronen )
f  tot  0 für En  1 MeV ( Spalt-Neutronen )
 Thermalisierung der Neutronen durch Vielfachstreuung in einem Moderator ist notwendig
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Absorptions- und Spaltquerschnitte für Neutronen
Die bei der Spaltung ausgelösten Neutronen
können an einer Reihe unterschiedlicher
Reaktionen teilnehmen und für weitere
Spaltungen verloren gehen.
0.0253 eV
Beispiel: (n,γ) Absorptionsreaktion
n + U → U* → U + γ
thermisch
Für 238U ist der WQ für inelastische
Stoßprozesse σ(n,n‘γ) größer als der
Spaltquerschnitt σ(n,f). In 238U kann keine
Kettenreaktion stattfinden.
Eine Kettenreaktion ist nur mit thermischen
Neutronen und Spaltung von 235U möglich:
→ Abbremsen (Moderation) der Neutronen.
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Absorptions- und Spaltquerschnitte für Neutronen
Wir beginnen mit thermischen Neutronen,
η gibt die mittlere Zahl der Spaltneutronen pro
thermischem Neutron an.

0.0253 eV
 fission

 fission   abs
0.72
 f
100
0.72
 capture 
 a
100
 fission 


U 




99.28
 f
100
99.28
235
U 
 a
100
235

U  4.20 b
238

U  3.43 b
238
thermisch
Für 235U: σf = 584 b und σa = 97 b, <ν>=2.4
Für 238U: σf = 0 b und σa = 2.1 b
Effektiver Wert von η = 1.3 für natürliches Uran
ist zu klein für Kettenreaktion.
→
235U
muß auf 3% angereichert werden
(η=1.8)
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Wechselwirkung von Neutronen in Materie
Abbremsung der Neutronen durch elastische Kernstöße:
nE n   A K  nEn   A K
Kinematik der Reaktion 
 E
v0
AE
10  21  2  m  M2  1  cos  cm 
E1 
nM n
n 
A 1  m
0  En  E n
0,992 E n  En  E n
Mittlerer Energieverlust der Neutronen pro Stoß:
Δ En
En
 1
En
En

 12 1   AA11 
2


Δ En
En
v1
v2
keine Anregung, kein Einfang,
keine Spaltung
 E  E
A 1
A  238
Beispiele:
M
m
 A2A12
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Thermalisierung der Neutronen
Δ En
En
Beispiel: Wasser ( H2O ) als Moderator  Streuung an Protonen, A  1
A 1
 50%
Grobabschätzung der Zahl k der Stöße bis zur Thermalisierung:
0,5k  E n  k BT 
1
40
eV  k  ln12 ln
En
k BT
E n  1MeV  k  25
Moderator
Mittlere Stoßzahl für
eine Abbremsung von
1,75 MeV auf 0.025 eV
Neigung zum Einfang
thermischer Neutronen
in relativen Einheiten
Wasserstoff
18
650
Deuterium
25
1
Beryllium
86
7
Kohlenstoff
114
10
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Weitere Neutronenverluste

238U-Absorption
 Reaktorgifte, z.B. das Spaltprodukt 135Xe: f ( 235U )  500 b
abs  3 000 000 b
 Steuermaterialien ( Cd, B )  kontrollierte Neutronen-Absorption
 Reaktorbrennstoff: tot( 235U )  f( 235U )
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Steuerung der Kettenreaktion
 Steuerstäbe:
Material mit großer Neutronen-Absorption: B, Cd, In, Ag
n  105B  37Li  24He  
114
n  113
48 Cd  48 Cd  
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Energiekonsum Mensch in Deutschland, Zahlen
Angaben in Leistung (Watt) = Energie / Zeit (Joule/sec) pro Kopf, im Jahresmittel
Umsatz des Körpers (Nahrung → Wärme)
100 Watt
Gesamtverbrauch an Primärenergie
(Zivilisation erhöht Verbrauch um Faktor 50 !!!)
5000 Watt
Gesamtverbrauch an Endenergie (2005)
Elektrischer Stromverbrauch (inkl. Industrie)
Private Haushalte Raum- und Wasserwärme
3700 Watt
750 Watt
1000 Watt
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Chemische Energie
Chemische Energie ist Atomenergie im wahren Sinn des Wortes.
Ursprung chemischer Energie: Veränderung von
Bindungen zwischen Atome, den Molekülbausteinen.
12g Kohlenstoff-Verbrennung mit 32g Sauerstoff (O2)
Wärmeenergie: 393 kJ ~ 30 kJ/gC
Reaktion C + O2 → CO2 + 4.1 eV
Wärmeenergie (Q = m·c·ΔT, c = 4180 JK-1kg-1) :
30 kJ können 1 Liter Wasser um 70 Celcius erwärmen.
Elektrische Energie (W = Leistung mal Zeit) :
30 kJ können 100 Watt Lampe 5 Minuten lang leuchten.
Mechanische Energie (W = Masse · Erdbeschleunigung · Höhe) :
30 kJ können 70kg Masse 43 Meter hoch heben.
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Vergleich mit der Kohleverbrennung
Bei der Verbrennung von 1 kg Steinkohle erhält man eine
verfügbare Energiemenge von 8.14 kWh.
Bei der Kernspaltung von 1 kg Uran erhält man eine
verfügbare Energiemenge von 22 700 000 kWh.
Kernbindung
200 MeV ist wesentlich stärker als
molekulare Bindung 4.1 eV.
Uran ist daher als „Brennstoff“ dreimillionenmal
wirkungsvoller als Steinkohle
Bei Spaltung von 1 kg Uran wird so viel Energie frei
wie bei der Verbrennung von 2800000 kg Kohlenstoff
zu 10.2 Millionen kg Kohlendioxid!!!
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Kernreaktor (Funktionsprinzip)
Reaktorkern enthält
→ Brennstoff
angereichertes Uran mit ca. 3% U-235
(Vergleich: Anreicherung bei Bombe: 80% U-235)
→ Moderator
Wasser unter hohem Druck (150 bar), zur
Abbremsung der Neutronen (erhöht
Spaltwahrscheinlichkeit) und zur Kühlung
(Spaltenergie geht in kinetische Energie der
Staltprodukte, die den Brennstoff erwärmt)
Bewegliche Kontrollstäbe (B, Cd, Gd) zur
gesteuerten Absorption von Neutronen, so dass
k=1 (kritisch) zur Aufrechterhaltung der
Kettenreaktion
→ Absorber
Ein Brennstab und Uranoxid-Pellets, der
Brennstoff der meisten Leistungsreaktoren.
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Von der Brennstofftablette bis zum Reaktorkern
Brennstoff in Form
von Brennelementen,
ca. 200 davon, jedes
individuell wassermoderiert u. ~gekühlt.
Jedes Element enthält
20-30 Brennstäbe,
jeder Brennstab enthält
200 Uranoxidtabletten
Grösse einer Tablette:
1 cm hoch, 1 cm
Durchmesser.
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Neutronenbilanz in einem Reaktor
Start:
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Reaktordynamik
Neutronenlebensdauer:
 thermischer Reaktor: ~ 20 μs
 schneller Reaktor: ~ 0.5 μs
Vermehrungsfaktor (Reaktivität):
keff 
Neutronenproduktionsrate
Neutronenverlustrate
 k<1 Reaktor fährt runter
 k=1 konstante Leistung
 k>1 Reaktor fährt rauf
Wie wird ein Reaktor stabil betrieben?
Annahme: k=1.001
 nach 1 s: 50000 Generationen
 Leistungsverstärkung pro Sekunde:
1.00150000  5 10 21
Wieso explodiert der Reaktor nicht?
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Reaktordynamik
Wie wird ein Reaktor stabil betrieben?
0.5% der Neutronen aus 235-U treten
verzögert um ca. 10 s aus den
Spaltbruchstücken aus
 k<1: unterkritischer Reaktor
 1<k<1+β: verzögert kritischer Reaktor
 k>1+β: prompt kritischer Reaktor
Beispiele für die Änderung der
Reaktivität im Betrieb:
 Abbrand von Kernbrennstoff
 Konversion (“Brüten”) durch
Neutronenbeschuss
U  n  239U  239Np  239Pu
238
Th  n  233Th  233Pa  233U
232
 Zerfall von Spaltstoffen
 Zugabe von Neutronengiften
(z.B. Bor im Wasser, Regelstäbe)
 Änderung von Moderator-Brennstoff
Verhältnis
Dichteänderung von Wasser (Temperatur)
Blasenbildung (pos./ neg. Reaktivitätskoeffizient)
Wasserverlust
 Reaktivitätsminderung durch
Dopplerverbreiterung der
Reaktionsquerschnitte bei hoher Temperatur

MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Reaktordynamik
Beispiele für die Änderung der
Reaktivität im Betrieb:
 Xenon-Berg: 135Xe ist Neutronengift
135
J

 135Cs
Xe  n 136 
 Xe

Beim Reduzieren der Reaktorleistung entsteht
ein Überschuss von 135Xe (Neutronengift), der
die Reaktivität noch weiter runterfährt und erst
nach vielen Stunden wieder verschwindet.
135
Beim Betrieb wird 135Xe durch
Neutronenbeschuss kontinuierlich abgebaut
In Tschnobyl wurden alle Regelstäbe
herausgefahren um ein Abschalten des
Reaktors durch den Xe-Berg zu
verhindern. Dann stieg die Leistung
plötzlich so schnell, dass die Stäbe
nicht schnell genug wieder reingefahren
werden konnten. Der positive Blasenkoeffizient ließ die Reaktivität weiter
ansteigen. Erst das explosionsartige
Herausschleudern des Brennstoffs
machte den Reaktor unterkritisch.
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Energieumwandlung in einem Kernkraftwerk
• Freisetzung der Kernbindungsenergie bei der Spaltung
• Die Umwandlung dieser Energie in Bewegungsenergie der erzeugten Spaltprodukte.
• Wärmeenergie durch das Abbremsen der Teilchen (Neutronen) im festen
Kernbrennstoff
• Nutzen der Wärmeenergie durch Erhitzen und Verdampfen eines Kühlmittels (Wasser)
• Wasserdampf wird auf Turbine geleitet
• Umwandlung der Bewegungsenergie der Turbine in elektrische Energie über den
Generator
• Einspeisung der Elektrizität in das Verbundnetz
• Die Abwärme muss entweder direkt (z.B. an einem Fluß) oder indirekt (z.B. über
Kühltürme in die Luft) an die Umwelt abgegeben werden.
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Energieumwandlung bei einem Siedewasserreaktor
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Energieumwandlung bei einem Druckwasserreaktor
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Siedewasser-Druckröhrenreaktor von Tschernobyl
Der mit Graphit moderierte Siedewasser-Druckröhrenreaktor von Tschernobyl. (Kann natürliches Uran verwenden)
Brennelemente hängen in ca. 1660 Druckröhren in senkrechten Bohrungen im Graphit, 210 Steuer- und Absorberstäbe.
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Nachzerfallswärme
Durch Zerfallsenergie
glühendes Pellet aus
Plutoniumdioxid.
Nachzerfallswärme als Anteil der Nennleistung nach Schnellabschaltung, berechnet nach zwei
verschiedenen Modellen: Retran ohne Berücksichtigung eines vorherigen Betriebs und Todreas unter
Annahme von 2 Jahren Betrieb vor Abschaltung. (WIKIPEDIA)
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Nachzerfallswärme nach 11 Monaten Betrieb
Wird ein Reaktor für die Dauer T0 [s] mit der Leistung P0 betrieben, so ist die Nachzerfallsleistung P zum
0.2
2
0.2
Zeitpunkt t [s] nach dem Abschalten des Reaktors Pt   P0  6.22 10  t  T0  t  
Zeit nach
Abschaltung
Nachzerfallswärme
in Prozent
Thermische Leistung
bei 4000 MW vor
Abschaltung
10 Sekunden
3,72 %
149 MW
100 min
1 Minute
2,54 %
102 MW
146 min
1 Stunde
1,01 %
40 MW
6h
1 Tag
0,44 %
18 MW
14 h
3 Tage
0,31 %
13 MW
20 h
1 Woche
0,23 %
9 MW
26 h
1 Monat
0,13 %
5 MW
49 h
3 Monate
0,07 %
3 MW
89 h
Zeit für die Erwärmung von
2500 m³ Wasser von 15 °C auf 100 °C
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Abklingbecken
Bei einem Leck oder Ausfall der Kühlung kann das
Abklingbecken auslaufen bzw. das Wasser verdampfen und
(teilweise) trockenlaufen. In diesem Fall können sich die
dort gelagerten Brennelemente übermäßig erhitzen.
Ist im Becken dabei noch Wasser vorhanden, kann bei ca.
8000 C das Zircaloy der Hüllenrohre mit dem Wasserdampf
in einer exothermen Redox-Reaktion zu Zirconiumoxid und
Wasserstoff reagieren und sich in kurzer Zeit ein explosives
Knallgasgemisch bilden.
Bei kompletter Trockenlegung der Brennstäbe können diese
in Brand geraten, was eine Zerstörung der Brennelemente
zur Folge hat.
MP-41 Teil 2: Physik exotischer Kerne, SS-2012
Welt Kernenergie
 443 Kernreaktoren in 30 Ländern (Jan. 2006)
 ~16% der Welt Energie Produktion (2003)
 24 Reaktoren sind im Bau
MP-41 Teil 2: Physik exotischer Kerne, SS-2012