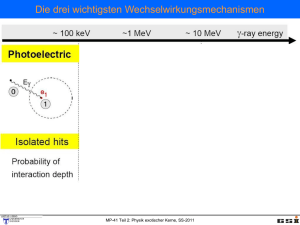
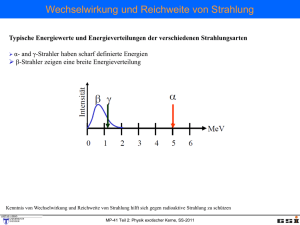
N=20
Werbung

MP-41 Teil 2: Physik exotischer Kerne 15.4.Einführung, Produktion exotischer Kerne – I 29.4.Produktion exotischer Kerne – II 6.5. Alpha-Zerfall, Zweiprotonen-Radioaktivität, Kernspaltung 13.5.Beta-Zerfall ins Kontinuum und in gebundene Zustände 20.5.Exkursion zum Radioteleskop in Effelsberg 27.5.Halo-Kerne 3.6. Tutorium-1 10.6.Kernspektroskopie und Nachweisgeräte 17.6.Anwendungen exotischer Kerne 24.6.Tutorium-2 1.7. Schalenstruktur fernab der Stabilität 8.7. Tutorium-3 15.7.Klausur MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Die Nuklidkarte Spiegelkerne und das nukleare Schalenmodell 70 40 MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Schalenstruktur fernab der Stabilität • Einleitung • Schalenstruktur superschwerer Kerne • Kernstruktur von Transfermium Elemente ( 250Fm, 254No) • deformiertes Schalenmodell • Nukleares Schalenmodell • klassische Anomalien: 11Be, 11Li • exp. Ergebnisse des Deuterons • Monopolwechselwirkung der Tensorkraft • Kerne um N=20: 40Ca, 38Ar, 36S, 34Si, 32Mg, 30Ne • Kerne um N=28: 48Ca, 46Ar, 44S • Zusammenfassung und Ausblick MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Spektroskopie von Transfermium Kernen (Z=100-103) Super – Heavy Elements MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Nukleare Schalenstruktur Wo ist der nächste Schalenabschluss ? Die Deformation des Kerns verändert die Reihenfolge der Einteilchenzustände ( Nilsson Modell ) MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Deformiertes Schalenmodell Nilsson-Modell • deformiertes Oszillatorpotenzial • axiale Symmetrie um z-Achse → Kerne können rotieren x y x y z 30 Hamiltonian H 2 m 2 x 2 y 2 2z z 2 C L S D L2 2m 2 Deformationsparameter δ 2 3 2 20 1 H 4 3 2z 20 1 2 m 4 5 20 r 2 C L S D L2 m 02 r 2 Y20 , 2m 2 3 4 Schalenmodell mit H.O.Potential Hdef MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Trennung von Laborsystem und körperfestes (intrinsisches) System K = Projektion des EinteilchenDrehimpulses auf die Symmetrieachse Rotation senkrecht zur Symmetrieachse ändert nicht die K-Quantenzahl Deformiertes Schalenmodell Orbital 1 ist näher am Schwerpunkt als Orbital 2. Die Energie von Orbital 1 ist am niedrigsten. Nilsson-Modell • deformiertes Oszillatorpotenzial • axiale Symmetrie um z-Achse → Kerne können rotieren x y x y z 30 Hamiltonian H 2 m 2 x 2 y 2 2z z 2 C L S D L2 2m 2 Deformationsparameter δ 2 3 2 20 1 H 4 3 2z 20 1 2 m 4 5 20 r 2 C L S D L2 m 02 r 2 Y20 , 2m 2 3 4 Schalenmodell mit H.O.Potential Hdef MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Deformiertes Schalenmodell Orbital 1 ist näher am Schwerpunkt als Orbital 2. Die Energie von Orbital 1 ist am niedrigsten. Nilsson-Modell • deformiertes Oszillatorpotenzial • axiale Symmetrie um z-Achse → Kerne können rotieren Intruder Orbital wird soweit angehoben oder abgesenkt, dass es Orbitale aus einer anderen Schale entgegengesetzter Parität kreuzt MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Deformiertes Schalenmodell Welche Struktur haben die SHE ? (indirekter Versuch) Deformierte Schalenabschlüsse für Transfermium Elemente 254No Oblate 152 β2~0.28 Prolate MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Stabilität der schweren Elemente 254No (Z=102) und 252Fm (Z=100) mit N=152 scheinen stabiler zu sein als ihre Nachbarn MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Woods-Saxon Niveaus Exp. Ergebnisse: Anregung von isomeren Zuständen 254No 250Fm mit Z=102 und N=152 – Protonen werden leicht angeregt mit Z=100 und N=150 – Neutronen werden leicht angeregt MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Yrast – plot ( 254No) MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Die magischen Zahlen nahe den stabilen Kernen 1 2 Es 2 1 2 Vs 2 1 2 Maria Goeppert-Mayer (1906-1972) Hans Jensen (1907-1973) Magische Zahlen mit konstanten Schalenabschlüssen sind nicht so robust, wie wir dachten. MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Nukleare Schalenstruktur Experimentelle Hinweise auf die magischen Zahlen E2 1 Kerne mit magischen Zahlen für Neutronen / Protonen: hohe Energien der 21+ Zustände kleine B(E2; 21+→0+) Werte Übergangswahrscheinlichkeiten werden in Weisskopf Einheiten (spu) gemessen B( E 2; 21 0 ) Was passiert weitab des Tals der Stabilität? MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Extremes Einteilchen-Schalenmodell Energie des Schalenabschlusses: BE (179F7 ) BE (168O8 ) E (0 d 5 / 2 ) 17 9 17 8 F8 O9 pos. Parität BE (157N 8 ) BE (168O8 ) E (0 p1/ 2 ) E 0 d 5 / 2 E (0 p1/ 2 ) BE (179F8 ) BE (157N8 ) 2 BE (168O8 ) 11.526 MeV BE (178O9 ) BE (168O8 ) E (0 d 5 / 2 ) 16 8 O8 BE (158O7 ) BE (168O8 ) E (0 p1/ 2 ) E 0 d 5 / 2 E (0 p1/ 2 ) BE (178O9 ) BE (158O7 ) 2 BE (168O8 ) 11.519 MeV 15 7 15 8 O7 N8 neg. Parität Gute Voraussage von Spin Parität π = (-1)ℓ magnetisches Moment Proton Neutron MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Einteilchen-Energien 8 2 17O: 17 8 O9 1/2 - Zustand schon bei 3.1 MeV Restwechselwirkung wird benötigt, verringert Abstand zwischen Schalen Einteilchen Zustände beobachtet in ungerade-A Kernen (besonders ein Nukleon + doppelt magischer Kern wie 4He, 16O, 40Ca) sind charakterisiert durch die Einteilchen-Energien des Schalenmodellbilds. MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Klassisches Beispiel einer Anomalie Mehrere Anomalien wurden in Schalenstrukturen von exotischen Kernen beobachtet: protonenreich oder neutronenreich erwartet ! 13 6 C7 ( stable) 11 4 Be7 (neutron rich ) Das 2s1/2 Orbital (Parität +) und das 1p1/2 Orbital (Parität -) sind invertiert ?? (parity inversion) MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Bildung von Halos und das s-Orbital Die s Komponente im Grundzustand ist essenziell für die Ausbildung einer Halostruktur. 2 2 V (r ) (r ) E (r ) 2 Schrödinger Gleichung: (r ) un (r ) Ym ( , ) d 2u 2 du 2 1 2 E V ( r ) ur 0 2 dr r dr r 2 Zentrifugalbarriere ( ℓ = 0 für s-Welle ) Neutronenreiche Kerne (11Be, 11Li) → instabil: flaches Kernpotential → die Wellenfunktion ist ausgedehnt → für s-Orbitale, die radiale Ausdehnung ist nicht blockiert durch die Zentrifugalbarriere ( Halo ) MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Halo-Kerne Anomalien der Schalenstruktur wurden zuerst beobachtet in 11Be (Z=4, N=7) 11Li (Z=3, N=8) , und die bekannt sind als ein-Neutron Halo und zwei-Neutron Halo-Kerne. MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Änderung der magischen Zahl nahe N=8; 12Be Ändert sich die magische Zahl nur bei Halo Kernen ? Nein! Gilt auch für 12Be. Diese Beobachtung weist auf eine universelle Evolution der Schalenstruktur. MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Theoretische Erklärung Die spezifische Proton-Neutron Wechselwirkung ( Monopolterm der Tensor-Kraft ) kann die Einteilchen-Anordnung verändern, abhängig von dem Proton-Neutron Verhältnis der Kerne. Die stark attraktive p-n Kraft zwischen J> and J< Orbitalen : 1 / 2 : 1 / 2 ( zum Beispiel, π p3/2 and ν p1/2 ) MP-41 Teil 2: Physik exotischer Kerne, SS-2011 MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Deuteron: Spin und Parität Mögliche Kombinationen der Spins und des relativen Bahndrehimpulses: sn und s p parallel und 0 sn und s p antiparall el und 1 Die Kernkraft ist spinabhängig ! sn und s p parallel und 1 sn und s p parallel und 2 Der gemessene Kernspin des Deuterons ist J=1 J 2 J J 1 2 Experiment ! Parität des Deuterons: Eigenschaften der emittierten Gammastrahlung beim Neutroneneinfang am Proton ergibt, dass die Parität des Deuterons positiv (π = +1) ist. Aus den Eigenschaften der Kugelflächenfunktionen ergibt sich die Parität zu (-1)ℓ = +1 Experiment ! woraus folgt, dass nur gerade Bahndrehimpulse von ℓ = 0 und ℓ = 2 vorkommen können. MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Deuteron: Magnetisches Moment • Der gemessene Kernspin des Deuterons ist J = 1 • Die Parität des Deuterons ist positiv, nur gerade Bahndrehimpulse ℓ = 0 und ℓ = 2 . • Das magnetische Moment des Deuterons, welches sich z.B. durch Kernspinresonanz (NMR) bestimmen läßt, ergibt sich zu: 0.8574 K Der gyromagnetische Faktor g stellt die Proportionalitätskonstante zwischen dem magnetischen Moment eines Teilchens und dem Spin dar (im Falle des Drehimpulses g = 1): g Mit S dem Spin-Operator und K e S g K S 2 mp c e dem Kern-Magneton 2 mp c Für ein punktförmiges Proton (s=1/2) erwartet man g = 2. Die innere Struktur von Proton (uud) und Neutron (udd) zeigt sich in den experimentellen Werten gsproton = 5.5857, gsneutron = -3.8261 Bei einer parallelen Ausrichtung der Nukleonenspins S = 1 und einem angenommenen Bahndrehimpuls von ℓ = 0 bzw. ℓ = 2 ergibt die Summe der magnetischen Momente von Proton und Neutron J , , S deuteron N 4 J J 1 g sproton g sneutron J J 1 1 S S 1 J J 1 1 S S 1 J 1, 0, S 1 deuteron 1 / 2 g sproton g sneutron 0.88 J 1, 2, S 1 deuteron 1 / 4 3 g sproton g sneutron 0.31 Die Wellenfunktion des Deuterons besteht zu 96% aus einem ℓ = 0 Zustand und 4% aus einem ℓ = 2 Zustand MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Deuteron: Quadrupolmoment • Der gemessene Kernspin des Deuterons ist J = 1 • Die Parität des Deuterons ist positiv, nur gerade Bahndrehimpulse ℓ = 0 und ℓ = 2 . • Das magnetische Moment des Deuterons ergibt sich zu 0.8574 K Der Bahndrehimpuls hat zu 4% den Wert ℓ = 2 • Das Deuteron ist nicht sphärisch. Es hat ein experimentell bestimmtes Quadrupolmoment von Q = 0.00282 eb. Das freie Neutron und das freie Proton haben kein elektrisches Quadrupolmoment. Das Deuteron kann nur aufgrund der Bahnbewegung ℓ = 2 von Proton und Neutron ein Quadrupolmoment besitzen. Qzz r r 2 3 cos 2 1 d Eine reine ℓ = 0 Wellenfunktion hat aufgrund ihrer Rotationssymmetrie ein verschwindendes Quadrupolmoment. Die Kernkraft ist spinabhängig ! Die Kernkräfte müssen ein Drehmoment aufbringen, das vom Radius r und dem Winkel θ abhängt. Wenn die Kernkraft von r und θ abhängt, gibt es eine nicht-zentrale Kraftkomponente eine MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Tensorkraft Nukleon-Nukleon Potentials abstoßender Teil ω (3π) - Austausch Alle Beiträge der N-N Wechselwirkung basieren auf dem Meson Austausch Mechanismus langreichweitiger Teil 1π – Austausch konstanter Abstand zwischen Nukleonen ~ 1fm → konstante Kerndichte 1π – Austausch ~ Tensor Kraft (r,θ) Potenzialmulde durch σ – Austausch ( 2π zu Spin 0 gekoppelt) g 2 e r ˆ Yukawa Potential: V r1 , r2 spin function 4 r m(π) ≈ 140 MeV/c2 m(σ) ≈ 500-600 MeV/c2 m(ω) ≈ 784 MeV/c2 MP-41 Teil 2: Physik exotischer Kerne, SS-2011 MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Effektive Einteilchen Energie effective single-particle energy ESPE ESPE is changed by N vm Monopole interaction, vm N particles ESPE : Total effect on singleparticle energies due to interaction with other valence nucleons MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Anschauliches Bild des Monopoleffekts der Tensorkraft Nukleon-Nukleon Restwechselwirkung wave function of relative motion spin of nucleon large relative momentum small relative momentum attractive repulsive Monopolenergie der Tensor-Wechselwirkung: V T j, j ' 2 J 1 jj ' V 2 J 1 J jj ' JT J T. Otsuka et al., Phys. Rev. Lett. 95, 232502 (2005), Phys. Rev. Lett. 97, 162501 (2006) MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Anschauliches Bild des Monopoleffekts der Tensorkraft Nukleon-Nukleon Restwechselwirkung Das Beispiel zeigt die Protonenkonfiguration (0p3/2) von 14C8. Je mehr Protonen im 0p3/2 Orbital sind, um so mehr wird das 0p1/2 Neutronenorbital angezogen und der Schalenabschluss bei N=8 entwickelt sich. Für 12Be8 wird das Protonenorbital 0p3/2 geleert, die Wechselwirkung ist geringer und das Neutronenorbital 0p 1/2 wird angehoben. j'< j'< j'> j'> j< j< j> j> proton neutron proton T. Otsuka et al., Phys. Rev. Lett. 95, 232502 (2005), Phys. Rev. Lett. 97, 162501 (2006) MP-41 Teil 2: Physik exotischer Kerne, SS-2011 neutron Anschauliches Bild des Monopoleffekts der Tensorkraft Nukleon-Nukleon Restwechselwirkung Das Beispiel zeigt die Protonenkonfiguration (0p3/2) von 14C8. Je mehr Protonen im 0p3/2 Orbital sind, um so mehr wird das 0p1/2 Neutronenorbital angezogen und der Schalenabschluss bei N=8 entwickelt sich. Für 12Be8 wird das Protonenorbital 0p3/2 geleert, die Wechselwirkung ist geringer und das Neutronenorbital 0p 1/2 wird angehoben. T. Otsuka et al., Phys. Rev. Lett. 95, 232502 (2005), Phys. Rev. Lett. 97, 162501 (2006) MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Der Effekt der Tensorkraft auf die ℓs-Kopplung 17F(16O+p) 23F(22O+p) VT() VT() 0d3/2 1s1/2 0d3/2 1s1/2 0d5/2 0d5/2 0p1/2 0p3/2 0p1/2 0p3/2 0s1/2 The tensor force does not act 0s1/2 The tensor force reduces the ℓs-splitting MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Michimasa et al. (from NPA 787 (2007) 569) 3/2+ 0d3/2 1s1/2 0d5/2 5 MeV 23F 5/2+ 17F Bohr & Mottelson vol. 1 Anwendung auf andere Schalen 32 12 low-lying 2+ MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Mg 20 Nukleare Schalenstruktur Experimentelle Hinweise auf die magischen Zahlen N=20 N=20 E(2+) [MeV] N=20 12 16 20 24 N N=28 Z=20 40Ca Z=18 38Ar Z=16 36S 44S Z=14 34Si 42Si Z=12 32Mg 40Mg Z=10 30Ne 38Ne Hinweise auf das nukleare Schalenmodell: hohe Energien der 21+ Zustände für Kerne mit magischen Zahlen MP-41 Teil 2: Physik exotischer Kerne, SS-2011 42Ca 44Ca 46Ca 48Ca 46Ar Monopol-Wechselwirkung der Tensorkraft Experimentelle Hinweise auf die magischen Zahlen N=20 40 20 Ca20 f7/2 E(2+) [MeV] N=20 12 N=20 d3/2 s1/2 d5/2 MP-41 Teil 2: Physik exotischer Kerne, SS-2011 16 20 24 N Monopol-Wechselwirkung der Tensorkraft Experimentelle Hinweise auf die magischen Zahlen N=20 38 18 Ar20 f7/2 E(2+) [MeV] N=20 12 N=20 d3/2 s1/2 d5/2 MP-41 Teil 2: Physik exotischer Kerne, SS-2011 16 20 24 N Monopol-Wechselwirkung der Tensorkraft Experimentelle Hinweise auf die magischen Zahlen N=20 36 16 S 20 f7/2 E(2+) [MeV] N=20 12 N=20 d3/2 s1/2 d5/2 MP-41 Teil 2: Physik exotischer Kerne, SS-2011 16 20 24 N Monopol-Wechselwirkung der Tensorkraft Experimentelle Hinweise auf die magischen Zahlen N=20 34 14 Si20 f7/2 E(2+) [MeV] N=20 12 N=20 d3/2 ( j< ) s1/2 ( j> ) d5/2 MP-41 Teil 2: Physik exotischer Kerne, SS-2011 16 20 24 N Monopol-Wechselwirkung der Tensorkraft Experimentelle Hinweise auf die magischen Zahlen N=20 32 12 Mg 20 f7/2 E(2+) [MeV] N=20 12 N=20 d3/2 ( j< ) s1/2 ( j> ) d5/2 MP-41 Teil 2: Physik exotischer Kerne, SS-2011 16 20 24 N Monopol-Wechselwirkung der Tensorkraft Experimentelle Hinweise auf die magischen Zahlen N=20 30 10 Ne20 f7/2 E(2+) [MeV] N=20 d3/2 N=20 12 ( j< ) s1/2 ( j> ) d5/2 MP-41 Teil 2: Physik exotischer Kerne, SS-2011 16 20 24 N Nukleare Schalenstruktur Experimentelle Hinweise auf die magischen Zahlen N=20 Die Schalenstruktur wird durch die attraktive p-n Kraft zwischen J> and J< Orbitalen ( π d5/2 and ν d3/2 ) stark beeinflußt. MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Nukleare Schalenstruktur Experimentelle Hinweise auf die magischen Zahlen N=28 N=20 spherical Ca S Si N=28 Z=20 40Ca Z=18 38Ar Z=16 36S 44S Z=14 34Si 42Si Z=12 32Mg 40Mg Z=10 30Ne 38Ne 42Ca 44Ca 46Ca 48Ca 46Ar deformed Hinweis auf das nukleare Schalenmodell: + hohe Energien der 21 Zustände Nukleare Feldtheorie: Nukleare Vielteilchenproblem wird relativistisch gelöst mit der Konsequenz: attraktives Skalarfeld (S-V) repulsives Vektorfeld (S+V) für Kerne mit magischen Zahlen Relativistic quasi-particle random phase approximation MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Nukleare Schalenstruktur Große Ähnlichkeit zwischen den drei Zahlen des HO-Schalenmodells N=20 N=8 N=40 O. S. , MG Porquet PPNP (2008) Gleicher Mechanismus : - kleinere 2+ Energien bei N=8, 20 and 40 - Inversion zwischen normalen und Intruder Zuständen bei N=40 - Suche nach einem (super)deformierten 0+2 Zustand in 68Ni - Prüfe die extreme Deformation von 64Cr MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Nukleare Schalenstruktur SPIN –FLIP =0 INTERACTION Entwicklung der HO-Schalenabschlüsse d5/2 s1/2 p3/2 [ ] ] 3/2 Z=6 Z=2 p3/2 f7/2 d3/2 s1/2 16 14 of the d - d Role 5/2 3/2 interaction 14 d5/2 d5/2 d5/2 g9/2 40 p1/2 5/2 Role fpof 3/2 [ ] N=14 p f7/23/2 d3/2 N=28 N~20 Z=14 Z=8 f7/2 s p1/2 1/2 N~8 8 p 1/2 6 6 of the p - p Role interaction p3/2 3/2 p 1/2 p3/2 20 d5/2 [ d5/2 28 f7/2 the s1/2 d5/2 d5/2 g9/2 N~40 f5/2 34 p1/2 32 f7/2- f5/2 interaction ?p3/2 f7/2 28 f7/2 Z=28 Z=20 Large N/Z MP-41 Teil 2: Physik exotischer Kerne, SS-2011 N=50 Small gaps Neue magische Zahlen MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Zukunft: Kern- und Astrophysik MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Rare Isotope Beam Capabilities Worldwide MP-41 Teil 2: Physik exotischer Kerne, SS-2011