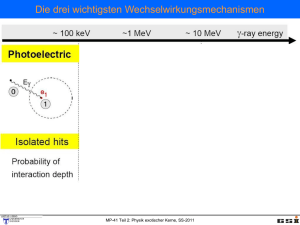
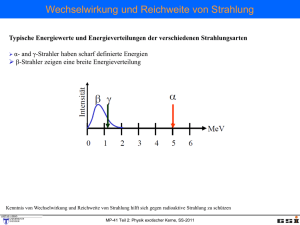
N=20
Werbung

MP-41 Teil 2: Physik exotischer Kerne 13.4. 20.4. 27.4. 4.5. 11.5. 18.5. 25.5. 1.6. 8.6. 15.6. 22.6. 29.6. 6.7. 13.7. Einführung, Beschleuniger Schwerionenreaktionen, Synthese superschwerer Kerne (SHE) Kernspaltung und Produktion neutronenreicher Kerne Fragmentation zur Erzeugung exotischer Kerne Halo-Kerne, gebundener Betazerfall, 2-Protonenzerfall Wechselwirkung mit Materie, Detektoren Schalenmodell Restwechselwirkung, Seniority Tutorium-1 Tutorium-2 Vibrator, Rotator, nukleare Isomere, Symmetrien Schalenstruktur fernab der Stabilität Tutorium-3 Klausur MP-41 Teil 2: Physik exotischer Kerne, SS-2012 New challenges in nuclear structure new magic numbers 126 doubly magic nuclei: 4He, 16O, 40Ca, 48Ca, 208Pb 82 protons 50 82 28 20 50 8 28 2 20 instable: 48Ni, 56Ni, 78Ni, 100Sn, 132Sn no 28O ! neutrons 2 8 MP-41 Teil 2: Physik exotischer Kerne, SS-2012 New challenges in nuclear structure new magic numbers 126 Sp = 0 82 proton drip-line explored up to Z = 83 protons 50 82 28 20 50 8 28 2 20 2 8 Sn = 0 neutrons neutron drip-line known up to N MP-41 = 20Teil!2: Physik exotischer Kerne, SS-2012 Die Nuklidkarte Spiegelkerne und das nukleare Schalenmodell 70 40 MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Schalenstruktur fernab der Stabilität • Einleitung • Schalenstruktur superschwerer Kerne • Kernstruktur von Transfermium Elemente ( 250Fm, 254No) • deformiertes Schalenmodell • Nukleares Schalenmodell • klassische Anomalien: 11Be, 11Li • exp. Ergebnisse des Deuterons • Monopolwechselwirkung der Tensorkraft • Kerne um N=20: 40Ca, 38Ar, 36S, 34Si, 32Mg, 30Ne • Kerne um N=28: 48Ca, 46Ar, 44S • Neutron-Proton Paarung in 92Pd • Zusammenfassung und Ausblick MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Spektroskopie von Transfermium Kernen (Z=100-103) Super – Heavy Elements MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Nukleare Schalenstruktur Wo ist der nächste Schalenabschluss ? J 3 254 102 No152 Die Deformation des Kerns verändert die Reihenfolge der Einteilchenzustände ( Nilsson Modell ) MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Deformiertes Schalenmodell Nilsson-Modell • deformiertes Oszillatorpotenzial • axiale Symmetrie um z-Achse → Kerne können rotieren x y x y z 30 Hamiltonian H 2 m 2 x 2 y 2 2z z 2 C L S D L2 2m 2 Deformationsparameter δ 2 3 2 20 1 H 4 3 2z 20 1 2 m 4 5 20 r 2 C L S D L2 m 02 r 2 Y20 , 2m 2 3 4 Schalenmodell mit H.O.Potential Hdef MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Trennung von Laborsystem und körperfestes (intrinsisches) System K = Projektion des EinteilchenDrehimpulses auf die Symmetrieachse Rotation senkrecht zur Symmetrieachse ändert nicht die K-Quantenzahl Deformiertes Schalenmodell Orbital 1 ist näher am Schwerpunkt als Orbital 2. Die Energie von Orbital 1 ist am niedrigsten. Nilsson-Modell • deformiertes Oszillatorpotenzial • axiale Symmetrie um z-Achse → Kerne können rotieren x y x y z 30 Hamiltonian H 2 m 2 x 2 y 2 2z z 2 C L S D L2 2m 2 Deformationsparameter δ 2 3 2 20 1 H 4 3 2z 20 1 2 m 4 5 20 r 2 C L S D L2 m 02 r 2 Y20 , 2m 2 3 4 Schalenmodell mit H.O.Potential Hdef MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Deformiertes Schalenmodell Orbital 1 ist näher am Schwerpunkt als Orbital 2. Die Energie von Orbital 1 ist am niedrigsten. Nilsson-Modell • deformiertes Oszillatorpotenzial • axiale Symmetrie um z-Achse → Kerne können rotieren Intruder Orbital wird soweit angehoben oder abgesenkt, dass es Orbitale aus einer anderen Schale entgegengesetzter Parität kreuzt MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Deformiertes Schalenmodell Welche Struktur haben die SHE ? (indirekter Versuch) Deformierte Schalenabschlüsse für Transfermium Elemente 254No Oblate 152 β2~0.28 Prolate MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Stabilität der schweren Elemente 254No (Z=102) und 252Fm (Z=100) mit N=152 scheinen stabiler zu sein als ihre Nachbarn MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Woods-Saxon Niveaus Exp. Ergebnisse: Anregung von isomeren Zuständen 254No 250Fm mit Z=102 und N=152 – Protonen werden leicht angeregt mit Z=100 und N=150 – Neutronen werden leicht angeregt MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Yrast – plot ( 254No) MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Die magischen Zahlen nahe den stabilen Kernen 1 2 Es 2 1 2 Vs 2 1 2 Maria Goeppert-Mayer (1906-1972) Hans Jensen (1907-1973) Magische Zahlen mit konstanten Schalenabschlüssen sind nicht so robust, wie wir dachten. MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Nukleare Schalenstruktur Experimentelle Hinweise auf die magischen Zahlen E2 1 Kerne mit magischen Zahlen für Neutronen / Protonen: hohe Energien der 21+ Zustände kleine B(E2; 21+→0+) Werte Übergangswahrscheinlichkeiten werden in Weisskopf Einheiten (spu) gemessen B( E 2; 21 0 ) Was passiert weitab des Tals der Stabilität? MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Extremes Einteilchen-Schalenmodell Energie des Schalenabschlusses: BE (179F7 ) BE (168O8 ) E (0 d 5 / 2 ) 17 9 17 8 F8 O9 pos. Parität BE (157N 8 ) BE (168O8 ) E (0 p1/ 2 ) E 0 d 5 / 2 E (0 p1/ 2 ) BE (179F8 ) BE (157N8 ) 2 BE (168O8 ) 11.526 MeV BE (178O9 ) BE (168O8 ) E (0 d 5 / 2 ) 16 8 O8 BE (158O7 ) BE (168O8 ) E (0 p1/ 2 ) E 0 d 5 / 2 E (0 p1/ 2 ) BE (178O9 ) BE (158O7 ) 2 BE (168O8 ) 11.519 MeV 15 7 15 8 O7 N8 neg. Parität Gute Voraussage von Spin Parität π = (-1)ℓ magnetisches Moment Proton Neutron MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Einteilchen-Energien 8 2 17O: 17 8 O9 1/2 - Zustand schon bei 3.1 MeV Restwechselwirkung wird benötigt, verringert Abstand zwischen Schalen Einteilchen Zustände beobachtet in ungerade-A Kernen (besonders ein Nukleon + doppelt magischer Kern wie 4He, 16O, 40Ca) sind charakterisiert durch die Einteilchen-Energien des Schalenmodellbilds. MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Klassisches Beispiel einer Anomalie Mehrere Anomalien wurden in Schalenstrukturen von exotischen Kernen beobachtet: protonenreich oder neutronenreich erwartet ! 13 6 C7 ( stable) 11 4 Be7 (neutron rich ) Das 2s1/2 Orbital (Parität +) und das 1p1/2 Orbital (Parität -) sind invertiert ?? (parity inversion) MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Bildung von Halos und das s-Orbital Die s Komponente im Grundzustand ist essenziell für die Ausbildung einer Halostruktur. 2 2 V (r ) (r ) E (r ) 2 Schrödinger Gleichung: (r ) un (r ) Ym ( , ) d 2u 2 du 2 1 2 E V ( r ) ur 0 2 dr r dr r 2 Zentrifugalbarriere ( ℓ = 0 für s-Welle ) Neutronenreiche Kerne (11Be, 11Li) → instabil: flaches Kernpotential → die Wellenfunktion ist ausgedehnt → für s-Orbitale, die radiale Ausdehnung ist nicht blockiert durch die Zentrifugalbarriere ( Halo ) MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Erinnerung: Halokerne Was kann man an der Neutronen-Dripline erwarten? Wellenfunktion außerhalb des Potentials e r r r 2 r2 r dr e / r 4 r r dr e / r 2 r 2 E 0.05 E MeV [ fm 2 ] 2 2 2 Je kleiner die Bindungsenergie, je ausgedehnter die Wellenfunktion r 2 1 2 1 R 2 2 4 Sn E κ2 κ 1/κ ~ r 7 MeV 0.35 fm-2 0.6 fm-1 1.7 fm 1 MeV 0.05 fm-2 0.2 fm-1 4.5 fm 0.1 MeV 0.005 fm-2 0.07 fm-1 14 fm MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Halo-Kerne Anomalien der Schalenstruktur wurden zuerst beobachtet in 11Be (Z=4, N=7) 11Li (Z=3, N=8) , und die bekannt sind als ein-Neutron Halo und zwei-Neutron Halo-Kerne. MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Änderung der magischen Zahl nahe N=8; 12Be Ändert sich die magische Zahl nur bei Halo Kernen ? Nein! Gilt auch für 12Be. Diese Beobachtung weist auf eine universelle Evolution der Schalenstruktur. MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Theoretische Erklärung Die spezifische Proton-Neutron Wechselwirkung ( Monopolterm der Tensor-Kraft ) kann die Einteilchen-Anordnung verändern, abhängig von dem Proton-Neutron Verhältnis der Kerne. Die stark attraktive p-n Kraft zwischen J> and J< Orbitalen : 1 / 2 : 1 / 2 ( zum Beispiel, π p3/2 and ν p1/2 ) MP-41 Teil 2: Physik exotischer Kerne, SS-2012 MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Deuteron: Spin und Parität Mögliche Kombinationen der Spins und des relativen Bahndrehimpulses: sn und s p parallel und 0 sn und s p antiparall el und 1 Die Kernkraft ist spinabhängig ! sn und s p parallel und 1 sn und s p parallel und 2 Der gemessene Kernspin des Deuterons ist J=1 J 2 J J 1 2 Experiment ! Parität des Deuterons: Eigenschaften der emittierten Gammastrahlung beim Neutroneneinfang am Proton ergibt, dass die Parität des Deuterons positiv (π = +1) ist. Aus den Eigenschaften der Kugelflächenfunktionen ergibt sich die Parität zu (-1)ℓ = +1 Experiment ! woraus folgt, dass nur gerade Bahndrehimpulse von ℓ = 0 und ℓ = 2 vorkommen können. MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Deuteron: Magnetisches Moment • Der gemessene Kernspin des Deuterons ist J = 1 • Die Parität des Deuterons ist positiv, nur gerade Bahndrehimpulse ℓ = 0 und ℓ = 2 . • Das magnetische Moment des Deuterons, welches sich z.B. durch Kernspinresonanz (NMR) bestimmen läßt, ergibt sich zu: 0.8574 K Der gyromagnetische Faktor g stellt die Proportionalitätskonstante zwischen dem magnetischen Moment eines Teilchens und dem Spin dar (im Falle des Drehimpulses g = 1): g Mit S dem Spin-Operator und K e S g K S 2 mp c e dem Kern-Magneton 2 mp c Für ein punktförmiges Proton (s=1/2) erwartet man g = 2. Die innere Struktur von Proton (uud) und Neutron (udd) zeigt sich in den experimentellen Werten gsproton = 5.5857, gsneutron = -3.8261 Bei einer parallelen Ausrichtung der Nukleonenspins S = 1 und einem angenommenen Bahndrehimpuls von ℓ = 0 bzw. ℓ = 2 ergibt die Summe der magnetischen Momente von Proton und Neutron J , , S deuteron N 4 J J 1 g sproton g sneutron J J 1 1 S S 1 J J 1 1 S S 1 J 1, 0, S 1 deuteron 1 / 2 g sproton g sneutron 0.88 J 1, 2, S 1 deuteron 1 / 4 3 g sproton g sneutron 0.31 Die Wellenfunktion des Deuterons besteht zu 96% aus einem ℓ = 0 Zustand und 4% aus einem ℓ = 2 Zustand MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Erinnerung: Schalenmodell Magnetische Momente: Für den g-Faktor gj gilt: mit j g g s s g j j 2 2 2 j s j 2 j s s 2 j j j j g g s s j j 2 s 2 j j 2 2 j 2 g j j 1 1 3 / 4 g s j j 1 1 3 / 4 j 2 j j 1 1 1 1 s s 1 g j g g s g g s 2 2 j j 1 Einfache Beziehung für den g-Faktor von Einteilchenzuständen g g g Kern g s K 2 1 für j 1/ 2 MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Deuteron: Quadrupolmoment • Der gemessene Kernspin des Deuterons ist J = 1 • Die Parität des Deuterons ist positiv, nur gerade Bahndrehimpulse ℓ = 0 und ℓ = 2 . • Das magnetische Moment des Deuterons ergibt sich zu 0.8574 K Der Bahndrehimpuls hat zu 4% den Wert ℓ = 2 • Das Deuteron ist nicht sphärisch. Es hat ein experimentell bestimmtes Quadrupolmoment von Q = 0.00282 eb. Das freie Neutron und das freie Proton haben kein elektrisches Quadrupolmoment. Das Deuteron kann nur aufgrund der Bahnbewegung ℓ = 2 von Proton und Neutron ein Quadrupolmoment besitzen. Qzz r r 2 3 cos 2 1 d Eine reine ℓ = 0 Wellenfunktion hat aufgrund ihrer Rotationssymmetrie ein verschwindendes Quadrupolmoment. Die Kernkraft ist spinabhängig ! Die Kernkräfte müssen ein Drehmoment aufbringen, das vom Radius r und dem Winkel θ abhängt. Wenn die Kernkraft von r und θ abhängt, gibt es eine nicht-zentrale Kraftkomponente eine MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Tensorkraft Nukleon-Nukleon Potentials abstoßender Teil ω (3π) - Austausch Alle Beiträge der N-N Wechselwirkung basieren auf dem Meson Austausch Mechanismus langreichweitiger Teil 1π – Austausch konstanter Abstand zwischen Nukleonen ~ 1fm → konstante Kerndichte 1π – Austausch ~ Tensor Kraft (r,θ) Potenzialmulde durch σ – Austausch ( 2π zu Spin 0 gekoppelt) g 2 e r ˆ Yukawa Potential: V r1 , r2 spin function 4 r m(π) ≈ 140 MeV/c2 m(σ) ≈ 500-600 MeV/c2 m(ω) ≈ 784 MeV/c2 MP-41 Teil 2: Physik exotischer Kerne, SS-2012 MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Effektive Einteilchen Energie effective single-particle energy ESPE ESPE is changed by N vm Monopole interaction, vm N particles ESPE : Total effect on singleparticle energies due to interaction with other valence nucleons MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Anschauliches Bild des Monopoleffekts der Tensorkraft Nukleon-Nukleon Restwechselwirkung wave function of relative motion spin of nucleon large relative momentum small relative momentum attractive repulsive Monopolenergie der Tensor-Wechselwirkung: V T j, j ' 2 J 1 jj ' V 2 J 1 J jj ' JT J T. Otsuka et al., Phys. Rev. Lett. 95, 232502 (2005), Phys. Rev. Lett. 97, 162501 (2006) MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Anschauliches Bild des Monopoleffekts der Tensorkraft Nukleon-Nukleon Restwechselwirkung Das Beispiel zeigt die Protonenkonfiguration (0p3/2) von 14C8. Je mehr Protonen im 0p3/2 Orbital sind, um so mehr wird das 0p1/2 Neutronenorbital angezogen und der Schalenabschluss bei N=8 entwickelt sich. Für 12Be8 wird das Protonenorbital 0p3/2 geleert, die Wechselwirkung ist geringer und das Neutronenorbital 0p 1/2 wird angehoben. j'< j'< j'> j'> j< j< j> j> proton neutron proton T. Otsuka et al., Phys. Rev. Lett. 95, 232502 (2005), Phys. Rev. Lett. 97, 162501 (2006) MP-41 Teil 2: Physik exotischer Kerne, SS-2012 neutron Anschauliches Bild des Monopoleffekts der Tensorkraft Nukleon-Nukleon Restwechselwirkung Das Beispiel zeigt die Protonenkonfiguration (0p3/2) von 14C8. Je mehr Protonen im 0p3/2 Orbital sind, um so mehr wird das 0p1/2 Neutronenorbital angezogen und der Schalenabschluss bei N=8 entwickelt sich. Für 12Be8 wird das Protonenorbital 0p3/2 geleert, die Wechselwirkung ist geringer und das Neutronenorbital 0p 1/2 wird angehoben. T. Otsuka et al., Phys. Rev. Lett. 95, 232502 (2005), Phys. Rev. Lett. 97, 162501 (2006) MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Der Effekt der Tensorkraft auf die ℓs-Kopplung 17F(16O+p) 23F(22O+p) VT() VT() 0d3/2 1s1/2 0d3/2 1s1/2 0d5/2 0d5/2 0p1/2 0p3/2 0p1/2 0p3/2 0s1/2 The tensor force does not act 0s1/2 The tensor force reduces the ℓs-splitting MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Michimasa et al. (from NPA 787 (2007) 569) 3/2+ 0d3/2 1s1/2 0d5/2 5 MeV 23F 5/2+ 17F Bohr & Mottelson vol. 1 Anwendung auf andere Schalen 32 12 low-lying 2+ MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Mg 20 Nukleare Schalenstruktur Experimentelle Hinweise auf die magischen Zahlen N=20 N=20 E(2+) [MeV] N=20 12 16 20 24 N N=28 Z=20 40Ca Z=18 38Ar Z=16 36S 44S Z=14 34Si 42Si Z=12 32Mg 40Mg Z=10 30Ne 38Ne Hinweise auf das nukleare Schalenmodell: hohe Energien der 21+ Zustände für Kerne mit magischen Zahlen MP-41 Teil 2: Physik exotischer Kerne, SS-2012 42Ca 44Ca 46Ca 48Ca 46Ar Monopol-Wechselwirkung der Tensorkraft Experimentelle Hinweise auf die magischen Zahlen N=20 40 20 Ca20 f7/2 N=20 d3/2 s1/2 d5/2 E(2+) [MeV] N=20 12 MP-41 Teil 2: Physik exotischer Kerne, SS-2012 16 20 24 N Monopol-Wechselwirkung der Tensorkraft Experimentelle Hinweise auf die magischen Zahlen N=20 38 18 Ar20 f7/2 N=20 d3/2 s1/2 d5/2 E(2+) [MeV] N=20 12 MP-41 Teil 2: Physik exotischer Kerne, SS-2012 16 20 24 N Monopol-Wechselwirkung der Tensorkraft Experimentelle Hinweise auf die magischen Zahlen N=20 36 16 S 20 f7/2 N=20 d3/2 s1/2 d5/2 E(2+) [MeV] N=20 12 MP-41 Teil 2: Physik exotischer Kerne, SS-2012 16 20 24 N Monopol-Wechselwirkung der Tensorkraft Experimentelle Hinweise auf die magischen Zahlen N=20 34 14 Si20 f7/2 N=20 d3/2 s1/2 ( j> ) d5/2 ( j< ) E(2+) [MeV] N=20 12 MP-41 Teil 2: Physik exotischer Kerne, SS-2012 16 20 24 N Monopol-Wechselwirkung der Tensorkraft Experimentelle Hinweise auf die magischen Zahlen N=20 32 12 Mg 20 f7/2 N=20 s1/2 ( j> ) d5/2 N=20 ( j< ) E(2+) [MeV] d3/2 12 MP-41 Teil 2: Physik exotischer Kerne, SS-2012 16 20 24 N Monopol-Wechselwirkung der Tensorkraft Experimentelle Hinweise auf die magischen Zahlen N=20 30 10 Ne20 f7/2 d3/2 N=20 ( j< ) s1/2 ( j> ) d5/2 E(2+) [MeV] N=20 12 MP-41 Teil 2: Physik exotischer Kerne, SS-2012 16 20 24 N Nukleare Schalenstruktur Experimentelle Hinweise auf die magischen Zahlen N=20 Die Schalenstruktur wird durch die attraktive p-n Kraft zwischen J> and J< Orbitalen ( π d5/2 and ν d3/2 ) stark beeinflußt. MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Nukleare Schalenstruktur Experimentelle Hinweise auf die magischen Zahlen N=28 N=20 spherical Ca S Si N=28 Z=20 40Ca Z=18 38Ar Z=16 36S 44S Z=14 34Si 42Si Z=12 32Mg 40Mg Z=10 30Ne 38Ne 42Ca 44Ca 46Ca 48Ca 46Ar deformed Hinweis auf das nukleare Schalenmodell: + hohe Energien der 21 Zustände Nukleare Feldtheorie: Nukleare Vielteilchenproblem wird relativistisch gelöst mit der Konsequenz: attraktives Skalarfeld (S-V) repulsives Vektorfeld (S+V) für Kerne mit magischen Zahlen Relativistic quasi-particle random phase approximation MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Nukleare Schalenstruktur Große Ähnlichkeit zwischen den drei Zahlen des HO-Schalenmodells N=20 N=8 N=40 O. S. , MG Porquet PPNP (2008) Gleicher Mechanismus : - kleinere 2+ Energien bei N=8, 20 and 40 - Inversion zwischen normalen und Intruder Zuständen bei N=40 - Suche nach einem (super)deformierten 0+2 Zustand in 68Ni - Prüfe die extreme Deformation von 64Cr MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Nukleare Schalenstruktur SPIN –FLIP =0 INTERACTION Entwicklung der HO-Schalenabschlüsse d5/2 s1/2 p3/2 [ ] ] 3/2 Z=6 Z=2 p3/2 f7/2 d3/2 s1/2 16 14 of the d - d Role 5/2 3/2 interaction 14 d5/2 d5/2 d5/2 g9/2 40 p1/2 5/2 Role fpof 3/2 [ ] N=14 p f7/23/2 d3/2 N=28 N~20 Z=14 Z=8 f7/2 s p1/2 1/2 N~8 8 p 1/2 6 6 of the p - p Role interaction p3/2 3/2 p 1/2 p3/2 20 d5/2 [ d5/2 28 f7/2 the s1/2 d5/2 d5/2 g9/2 N~40 f5/2 34 p1/2 32 f7/2- f5/2 interaction ?p3/2 f7/2 28 f7/2 Z=28 Z=20 Large N/Z MP-41 Teil 2: Physik exotischer Kerne, SS-2012 N=50 Small gaps MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Excitation energy Signatures near closed shells Sn isotopes only valence neutrons MP-41 Teil 2: Physik exotischer Kerne, SS-2012 8+(g9/2)-2 seniority isomers in 98Cd and 130Cd N=50 Z=48 (8+) (6+) (4+) 2428 2281 2083 h11/2 d3/2 s1/2 d5/2 g7/2 N=82 N=50 MeV 2.6 2.2 1.6 0.5 0 (8+) (6+) (4+) participating neutron-orbitals (2+) (2+) 1395 2128 2002 1864 N=82 Z=48 1325 two proton holes in the g9/2 orbit No dramatic shell quenching! 0+ 0+ A. Blazhev et al., Phys. Rev. C69 (2004) 064304 A. Jungclaus et al., Phys. Rev. Lett. 99 (2007), 132501 MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Isoscalar neutron-proton pairing in 92Pd four proton holes in g9/2 orbit 46 48 50 Jmax=12 B. Cederwall et al., Nature 469 (2011), 68 T.S. Brock et al., Phys. Rev. C82 (2010) 061309 MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Neue magische Zahlen MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Zukunft: Kern- und Astrophysik MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Rare Isotope Beam Capabilities Worldwide MP-41 Teil 2: Physik exotischer Kerne, SS-2012