2 +
Werbung

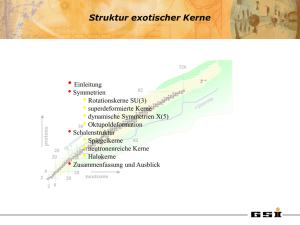
MP-41 Teil 2: Physik exotischer Kerne 15.4.Einführung, Produktion exotischer Kerne – I 29.4.Produktion exotischer Kerne – II 6.5. Alpha-Zerfall, Zweiprotonen-Radioaktivität, Kernspaltung 13.5.Beta-Zerfall ins Kontinuum und in gebundene Zustände 20.5.Exkursion zum Radioteleskop in Effelsberg 27.5.Halo-Kerne 3.6. Tutorium-1 10.6.Kernspektroskopie und Nachweisgeräte 17.6.Anwendungen exotischer Kerne 24.6.Tutorium-2 1.7. Schalenstruktur fernab der Stabilität 8.7. Tutorium-3 15.7.Klausur MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Struktur exotischer Kerne • Einleitung • Symmetrien • Isospin Symmetrie (Spiegelkerne: 54Ni, 54Fe) • Senioritäts-Paarung: 98Cd, 130Cd • Rotationskerne SU(3): 254No • superdeformierte Kerne: 152Dy • dynamische Symmetrien X(5) • Oktupoldeformation: 226Ra • Zusammenfassung und Ausblick MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Die Nuklidkarte – Ordnung der Atomkerne Eigenschaften nuklearer Materie MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Symmetrien Symmetrien helfen die Natur zu verstehen Untersuchung fundamentaler Symmetrien: eine Schlüsselfrage in der Physik Erhaltungsgesetze gute Quantenzahlen In nuclear physics, conserved quantities imply underlying symmetries of the interactions and help to interpret nuclear structure features MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Symmetrien in der Kernphysik p n Isospin Symmetrie: 1932 Heisenberg SU(2) n ) n ) 1901-1976 Nobelpreis 1932 p p Austauschkräfte mp = 938.3 MeV mn = 939.5 MeV Starke Wechselwirkung kann Proton/Neutron nicht unterscheiden Proton und Neutron sind für starke WW Zustände eines Teilchens (Nukleon) → Isospin MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Isospin Tz=1/2(Z-N) T=|Tz| Protonen und Neutronen sind 2 Zustände des gleichen Teilchens Pauli Prinzip verbietet T=0 Zustände für nn und 2He Deuteron (T=0,S=1) ist das einzige A=2 gebundene System Proton: Tz(p) = +1/2 Neutron: Tz(n) = -1/2 2He MP-41 Teil 2: Physik exotischer Kerne, SS-2011 nn Isospin Ist np Wechselwirkung gleich der nn und pp? Vergleiche die Energieniveaus für Kerne mit konstantem A. Gleiche Spin / Paritäts-Zustände haben die gleiche Energie. np=nn=pp MeV 5 nn 2He MeV T=1 multiplet 5 4 4 4+ 3 4+ 4+ 2 3 2 1 2+ 0 0+ 22 12 Mg10 0.693 4+ 3+ 2+ 2+ 1 0+ 0+ 0 T=0 singlet 22 11 Na11 MP-41 Teil 2: Physik exotischer Kerne, SS-2011 22 10 Ne12 Isospin Symmetrie in T=1 Kernen (abgesehen von der Coulomb Energie) natürlich, Vpp Vnn Vpn T=1 multiplet 22Mg • 22Ne 22Na Unterschiede in der Bindungsenergie bei Spiegelkernen (Bethe-Weizsäcker Formel) 22 22 BE (10 Ne) BE (12 Mg ) aCoul T=0 singlet • 10 9 12 11 10.6 MeV 221/ 3 Isobare-Massen-Multiplett Gleichung BE (i,Tz T) BE (i,Tz T) 2biT 3 Ze 5 R 2 ECoul ECoul 3 e2 2 3 A 2T 5 r0 Isovector ~ 3-15 MeV (~ A2/3) BE i, T , Tz ai biTz ciTz2 Isoscalar Dominated by the strong interaction ~ 100’s MeV MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Isotensor ~200-300 keV T=1 Isospin Symmetrie in pf-Schalenkernen Suche nach Abweichungen von Isospin Symmetrie Spiegelkerne 54Ni 50Fe 54 28 Ni26 54 26 Fe28 54Fe 46Cr 50Cr 46Ti MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Identifikation von 54Ni coincidence spectra gate on 54Ni 50 ns < t < 1 s MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Protonen Radioaktivität – Zerfall des Iπ=10+ Isomers in 54Ni Zerfall des angeregten 10+-Zustands durch Protonemission und -Strahlung D. Rudolph, R. Hoischen et al., Phys.Rev.C78 (2008), 021301 MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Symmetrien in der Kernphysik p n Isospin Symmetrie: 1932 Heisenberg SU(2) Spin-Isospin Symmetrie: 1936 Wigner SU(4) J 0 Senioritäts-Paarung: 1943 Racah MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Paarungskraft: Seniorität Seniorität ν ist die Zahl der Nukleonen, die nicht zu Paaren mit J=0 verknüpft sind. • Eine große Spin-Bahn Aufspaltung (magische Kerne) bedeutet ein jj-Kopplungsschema. • Die Paarwechselwirkung zwischen zwei Nukleonen in der j-Unterschale ist nur für ν=0 und J=0 verschieden von Null. • Die δ-Wechselwirkung liefert eine einfache geometrische Begründung für die Senioritäts-Spektren. MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Paarungskraft: Seniorität Seniorität ν ist die Zahl der Nukleonen, die nicht zu Paaren mit J=0 verknüpft sind. energy axis • Eine große Spin-Bahn Aufspaltung (magische Kerne) bedeutet ein jj-Kopplungsschema. • Die Paarwechselwirkung zwischen zwei Nukleonen in der j-Unterschale ist nur für ν=0 und J=0 verschieden von Null. Seniority scheme: min 4+ =2 j j j j j j J j 6+ =2 J j J E V0 Fr tan 2 2+ =2 0+ =0 • Die δ-Wechselwirkung liefert eine einfache geometrische Begründung für die Senioritäts-Spektren. MP-41 Teil 2: Physik exotischer Kerne, SS-2011 8+(g9/2)-2 seniority isomers in 98Cd and 130Cd N=50 Z=48 (8+) (6+) (4+) 2428 2281 2083 h11/2 d3/2 s1/2 d5/2 g7/2 N=82 N=50 MeV 2.6 2.2 1.6 0.5 0 participating N-orbitals (2+) (8+) (6+) (4+) (2+) 1395 two proton holes in the g9/2 orbit No dramatic shell quenching! 0+ 0+ MP-41 Teil 2: Physik exotischer Kerne, SS-2011 2128 2002 1864 1325 N=82 Z=48 Symmetrien in der Kernphysik p n Isospin Symmetrie: 1932 Heisenberg SU(2) Spin-Isospin Symmetrie: 1936 Wigner SU(4) J 0 j Senioritäts-Paarung: 1943 Racah Sphärische Symmetrie: 1949 Mayer MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Symmetrien in der Kernphysik p n Isospin Symmetrie: 1932 Heisenberg SU(2) Spin-Isospin Symmetrie: 1936 Wigner SU(4) J 0 j Senioritäts-Paarung: 1943 Racah Sphärische Symmetrie: 1949 Mayer Deformiertes Kernfeld (spontane Symmetrie Brechung) Symm. Wiederherstellung Rotationsspektren: 1952 Bohr-Mottelson SU(3) dynamische Symmetrie: 1958 Elliott MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Rotationsspektren in 254No JUROGAM + RITU am Target emittierte Gamma - Strahlung in Koinzidenz mit nachgewiesenen Rückstoßkernen 208Pb(48Ca,2n)254No 20 pnA auf 0.5 mg/cm2 Target σ = 2 μ barn → 800 Reaktionen pro Stunde ! Identifikation von 254No über Alpha-Zerfallsketten S. Eeckhaudt et al., Eur. Phys. J. A 26, 227 (2005) MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Rotationsspektren in 254No Rotationsenergie: Gamma – Energie: 2 EJ J J 1 2 EJ EJ 2 2 4 J 2 2 S. Eeckhaudt et al., Eur. Phys. J. A 26, 227 (2005) MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Rotationsbewegung eines deformierten Kerns Wir betrachten einen achsialsymmetrischen Kern 1 2 , der die gleiche Frequenz um die x- und y-Achse hat. Der Hamilton Operator ist dann J Rˆ i2 Rˆ 2 Rˆ 32 2 1 i 1 2 i 3 3 H rot Zustände mit Projektionen K und –K sind entartet Die Kernwellenfunktion muß dies zum Ausdruck bringen: man hat ein symmetrisiertes Produkt für einen rotierenden Kern 2 J 1 2 16 1/ 2 JMK DMJ K K 1 J K DMJ K K Für K=0, sind nur gerade J erlaubt, so daß die Wellenfunktion nur aus einem Term besteht 2 J 1 2 8 1/ 2 JM DMJ 0 0 Wird der Gesamtdrehimpuls nur durch die Rotation (J=R) erzeugt, so erhält man für die symmetrische Rotationsenergie Erot 2 J J 1 2 wobei nur gerade J erlaubt sind. MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Rotationsbande in deformierten Kernen MeV 0.519 2 EJ J J 1 2 γ-decay 2 2 EJ EJ 2 0.007 4MeV J 2 2 2 0.305 J 0.146 0.044 0 254 102 No Beachte – große bedeuten kleinere Abstände zwischen den Energieniveaus! r 2 Beachte: Rotationen um die Symmetrieachse 3 sind ununterscheidbar; Der Rotationsdrehimpuls muss immer senkrecht zur Symmetrieachse 3 stehen. dm MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Das Trägheitsmoment misst die Kerngestalt z Parameterisierung der Gestalt, des Quadrupolmoments und des Trägheitsmoments unter der Annahme einer konstanten Dichte: R R0 1 Y20 R() R0 1.2 A1/ 3 4 R 00 R 900 R 1.05 3 5 R0 R0 Trägheitsmoment eines starren Ellipsiods: R 2 M Ro2 (1 0.32 ) 5 Trägheitsmoment eines Flüssigkeitstropfens: F Quadrupolmoment: Q0 9 M Ro2 2 8 3 Z R02 5 MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Wirklichkeit ist irgendwie dazwischen... Das Trägheitsmoment misst die Kerngestalt 3 / rigid R0 1 Y20 R() R 1 R0 1.2 A1/ 3 deformation β 2 EJ J J 1 2 Aus dem gemessenen Spektrum kann man das Trägheitsmoment bestimmen ! Rotationsfrequenz: 0.75 MeV 2 10 20 Hz “Kerne sind wie Eierschalen, die mit einer Mischung aus normal und supraleitender Flüssigkeit gefüllt sind !" Supraleitung aufgrund der Paarkräfte in Analogie zu den Cooper Paaren (Elektronen) in Supraleitern. MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Das Trägheitsmoment misst die Kerngestalt 3 R0 1 Y20 R() R 2 EJ J J 1 2 Aus dem gemessenen Spektrum kann man das Trägheitsmoment bestimmen ! Rotationsfrequenz: 0.75 MeV 2 10 20 Hz “Kerne sind wie Eierschalen, die mit einer Mischung aus normal und supraleitender Flüssigkeit gefüllt sind !" Supraleitung aufgrund der Paarkräfte in Analogie zu den Cooper Paaren (Elektronen) in Supraleitern. MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Multipolentwicklung: Quadrupolmoment d r r Das elektrische Potential für eine beliebige Ladungsverteilung ist gegeben durch p r ' U r d ' r r' Entwicklung 1 r ' 4 1 Ym , Y*m ' , ' r r' 2 1 m 0 r Spezialfall: electrischer Monopol m 0 Y00 , Y00 ' , ' 1 1 r r' r MP-41 Teil 2: Physik exotischer Kerne, SS-2011 1 4 Multipolentwicklung: Quadrupolmoment d r r Das elektrische Potential für eine beliebige Ladungsverteilung ist gegeben durch U r p r ' r d ' homogene Ladungsverteilung p r ' Spezialfall: electrischer Monopol 3 Z e 4 R03 3 Z e 1 2 U r r ' dr ' sin ' d ' d ' 3 4 R0 r 3 Z e 1 R03 Z e U r 4 4 R03 r 3 r MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Multipolentwicklung: Quadrupolmoment d r Das elektrische Potential für eine beliebige Ladungsverteilung ist gegeben durch r p r ' U r d ' r r' Entwicklung 1 r ' 4 1 Ym , Y*m ' , ' r r' 2 1 m 0 r Multipol-Moment M * , m p r ' r ' Y*m ' , 'd ' Spezialfall: electrisches Quadrupolpotential Quadrupol-Matrixelement B(E2)-Wert: 2 5 m 2 4 3 1Z e R0 M , m 3 Y 2,m ,2 M * 2,Q U r 2 m0 4 16 5 r m 2 5 B( E 2; I I 2) Qt2 I K 2 0 / I 2 K 16 * MP-41 Teil 2: Physik exotischer Kerne, SS-2011 2 Rotationsspektren in 254No Yrast plot R.-D. Herzberg et al., Nature 442, 896 (2006) MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Superdeformation von 152Dy Trägheitsmoment → Deformation β=0.6 Achsenverhältnis 2:1 MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Kerndeformation und Rotation MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Erzeugung von Drehimpuls in Kernen MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Erzeugung von Drehimpuls in Kernen SU(3) SU(2) U(5) MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Symmetrien in der Kernphysik j Sphärische Symmetrie: 1949 Mayer J 0 J 2 Deformiertes Kernfeld (spontane Symmetrie Brechung) Symm. Wiederherstellung Rotationsspektren: 1952 Bohr-Mottelson SU(3) dynamische Symmetrie: 1958 Elliott Interacting Boson Model (IBM dynamische Symmetrie): 1974 Arima and Iachello Critical point symmetry E(5), X(5) …. 2000… F. Iachello MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Symmetrien in der Kernphysik Keine Restwechselwirkung ⇒ unabhängiges Teilchen Schalenmodell Restwechselwirkung: Paarwechselwirkung (jj Kopplung) ⇒ Racah´s SU(2) Quadrupolwechselwirkung (LS Kopplung) ⇒ Elliott´s SU(3) MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Kerngestalten und Symmetrien Energy Vibrator Transitional Spherical Kerne mit X(5) Symmetrie: P Rotor Soft N p Nn N p Nn ~5 Deformed p-dripline stable Deformation n-dripline prolate oblate Transitional nuclei R. F. Casten Nature Physics 2 (2006) 811 MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Dynamische Symmetrien in der Kernphysik Energy Gamma-soft-O(6) Spherical Transitional Vibrator-SU(5) Rotor-SU(3) Deformation MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Deformed Untersuchung fundamentaler Symmetrien in der Natur Y30 coupling Suche nach elektrischen Dipolmomenten (Verletzung der Zeitumkehrung) Q1 CLD A Ze 2 3 Statische Oktupol-Deformationen gibt es nur in ganz bestimmten Regionen der Nuklidkarte. + + + 226Ra + 88 + In oktupoldeformierten Kernen ist der Massen- und der Ladungsschwerpunkt getrennt wodurch ein nichtverschwindendes elektrisches Dipolmoment entsteht. MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Untersuchung fundamentaler Symmetrien in der Natur Rotation MP-41 Teil 2: Physik exotischer Kerne, SS-2011 Die Nuklidkarte Spiegelkerne und das nukleare Schalenmodell 126 82 protons 50 82 70 28 20 50 8 28 2 20 neutrons 2 8 MP-41 Teil 2: Physik exotischer Kerne, SS-2011 40