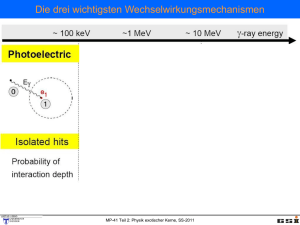
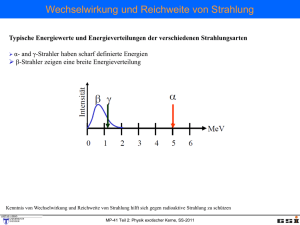
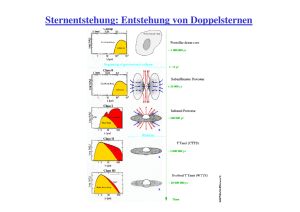
Detektoren
Werbung

MP-41 Teil 2: Physik exotischer Kerne 13.4. 20.4. 27.4. 4.5. 11.5. 18.5. 25.5. 1.6. 8.6. 15.6. 22.6. 29.6. 6.7. 13.7. Einführung, Beschleuniger Schwerionenreaktionen, Synthese superschwerer Kerne (SHE) Kernspaltung und Produktion neutronenreicher Kerne Fragmentation zur Erzeugung exotischer Kerne Halo-Kerne, gebundener Betazerfall, 2-Protonenzerfall Wechselwirkung mit Materie, Detektoren Schalenmodell Restwechselwirkung, Seniority Tutorium-1 Tutorium-2 Vibrator, Rotator, Symmetrien Schalenstruktur fernab der Stabilität Tutorium-3 Klausur MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Die drei wichtigsten Wechselwirkungsmechanismen MP-41 Teil 2: Physik exotischer Kerne, SS-2012 1. Germanium-Detektoren Wechselwirkung im Ge Kristall: Photoeffekt (niedrige Energie) ComptonStreuung Streuung Compton (mittlere Energie) +e- (hohe e+e- (hohe Energie) Paarerzeugung evon Energie) Leitungsband 0.7 eV 3 eV Valenzband Zahl der Elektronen-Loch Paare für 1 MeV, N = 106 / 3 = 3 105 Energieauf lösung N N 0.0018 1.8 keV E γ MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Compton unterdrückte Germanium-Detektoren Wechselwirkung im Ge Kristall: Photoeffekt (niedrige Energie) Compton Streuung (mittlere Energie) Paarerzeugung e+e- (hohe Energie) peak-to-total ratio unsuppressed P/T~0.15 Compton suppressed P/T~0.6 MP-41 Teil 2: Physik exotischer Kerne, SS-2012 EUROBALL (Legnaro / Strasbourg) 15 seven-fold Cluster detectors 30 coaxial detectors 26 four-fold Clover detectors MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Probleme beim Nachweis der γ-Strahlung E 2 keV 1. bewegte γ-Quelle nach Doppler-shift Korrektur 2. gleichzeitige Emission vieler γ-Quanten → γ-Ereignisse werden falsch addiert Lösung: elektrisch segmentierte Detectoren kleiner Öffnungswinkel gutes Tracking der γ-Strahlung MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Gamma-Ray Tracking Compton Streuung Pulsform-Analyse von 37 Signalen → (x, y, z, t, E) MP-41 Teil 2: Physik exotischer Kerne, SS-2012 MP-41 Teil 2: Physik exotischer Kerne, SS-2012 2. Silizium-Detektoren Das Prinzip des Teilchennachweises α-Teilchen Ionisation des Detektormaterials (Bethe-Bloch-Gleichung) → Erzeugung von freien Ladungsträgern Ladungssammlung in einem elektrischen Feld Elektronische Verstärkung und Registrierung des Signals Anzahl der erzeugten Ladungsträger ist proportional der deponierten Energie. → Energiemessung (Spektroskopie) Segmentierung der Elektroden oder Messung der Driftzeit erlaubt Ortsauflösung MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Prinzip eines Microstrip-Detektors MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Wiederholung: Bändermodell Materialeigenschaften MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Dotierung am Beispiel von Si Bei Einbau eines 5-wertigen Atoms (P, As, Sb) in ein Kristallgitter aus 4-wertigen Si-Atomen bleibt das 5. Valenzelektron des Fremdatoms ohne Bindungspartner. Donator, n-Dotierung Bei Einbau eines 3-wertigen Atoms (B, Al, Ga, In) in ein Kristallgitter aus 4-wertigen Si-Atomen kann eine Bindung eines angrenzenden Si-Atoms nicht abgesättigt werden. Akzeptor, p-Dotierung MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Der p-n Übergang Bringt man einen n- und einen p-Leiter in Kontakt, so muß im thermischen Gleichgewicht die Fermi-Energie identisch sein. Die Anpassung der zuvor unterschiedlichen Fermi-Niveaus wird erreicht durch die Diffusion der jeweiligen Majoritätsladungsträger in den anders dotierten Bereich. Dadurch baut sich am Übergang eine Raumladung auf, welche das weitere Eindringen von e- und Löchern in die Übergangszone verhindert. Es entsteht somit ein stabiler ladungsträgerfreier Bereich (Verarmungszone). E MP-41 Teil 2: Physik exotischer Kerne, SS-2012 3. Schema eines einfachen Gasdetektors Wichtige Kenngrößen: mittlerer Energieverlust dE/dx mittleres effektives Ionisationspotenzial pro Hüllenelektron Energieverlust pro erzeugten Elektron-Ion Paares mittlere Anzahl der primären und der gesamten Elektron-Ion Paaren Stoßionisation: wichtig für die Gasverstärkung des Detektors Wirkung elektronegativer Gase: wichtig für die Nachweiswahrscheinlichkeit Diffusion: beeinflußt die Ortsauflösung des Detektors elektrisches Feld: E r MP-41 Teil 2: Physik exotischer Kerne, SS-2012 V r ln rc / ra Gas-Ionisations-Zähler (Arbeitsbereiche) Neben der Detektorgeometrie und der Wahl des Zählgases bestimmt die angelegte Hochspannung wesentlich den Betriebsmodus eines Gasdetektors. Man kann in Abhängigkeit von der externen Hochspannung bestimmte Arbeitsbereiche angeben. Rekombinationseffekte Ionisationsbereich Gasverstärkung: e- Energie > Ionisationsenergie Proportionalbereich < 600 V Multiplikation ist linear Größere Spannung > 600 V Multiplikation wird nichtlinear Raumladung der pos. Ionen Geiger-Müller Bereich Positive Raumladung begrenzt E-Feldstärke, keine weitere Verstärkung, gleiche Amplitude Entladungsbereich Typisches Gas P10: 90% Ar und 10% CH4 MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Ionisationskammer Eine ideale Ionisationskammer wird in dem Spannungsbereich betrieben, in welchem einerseits die erzeugte Ladung vollständig gesammelt wird, andererseits aber noch keine Sekundärionisation stattfindet (also keine Gasverstärkung). Für elektr. Feldstärken von 500 V/cm und für typische Driftgeschwindigkeiten erhält man bei 10 cm Driftstrecke Sammelzeiten für e- von 2 μs und für Ionen von etwa 2 ms. Bildfolge: Signal für ein e--Ion Paar in einer planaren Ionisationskammer Das Signal wird durch die Bewegung der Elektronen und Ionen im elektrischen Feld induziert. MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Proportionalzähler Proportionalzähler nutzen Gasverstärkung durch Sekundärionisation für die Signalerzeugung. Die dafür übliche Geometrie ist eine zylindrische Kathode mit zentralem Anodendraht. Das dabei entstehende E-Feld ist ~1/r, d.h. in nächster Umgebung vom Anodendraht treten lokal sehr hohe Feldstärken auf. Für r ≤ rkrit sind Sekundärionisation möglich Querschnitt durch ein Proportionalzählrohr und elektrische Feldstärke E in Abhängigkeit vom Abstand zum Anodendraht. MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Proportionalzähler Durch Primärionisation erzeugte Elektronen driften auf den Anodendraht zu und gelangen so in Bereiche hoher lokaler Feldstärke. Sobald die elektrische Feldstärke Ekrit übersteigt, kommt es zur Sekundärionisation. Infolgedessen bildet sich eine tropfenförmige Ladungslawine um den Anodendraht aus. Die dabei erzeugten Elektronen driften schnell auf den Anodendraht zu und werden dort abgeleitet, während die Ionen sich langsam vom Anodendraht entfernen und zur Kathode wandern. MP-41 Teil 2: Physik exotischer Kerne, SS-2012 3.1 Vieldraht-Proportionalkammer MWPC Aufgabe: Messung der räumlichen Koordinaten einer Teilchenspur Georges Charpak Jeder Anodendraht arbeitet als unabhängiger Proportionalzähler - Zeitauflösung: schnelle Anodensignale (trise ~ 0.1ns) - Ortsauflösung: für d = 2 mm σx = 600 μm (Gewichtung mit Ladung) MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Vieldraht-Proportionalkammer (x-y) Will man eine zweidimensionale Ortsbestimmung, so kann man dies durch Segmentierung der Kathode erreichen. Die Kathode kann dann z.B. durch parallele Streifen, rechteckige Kathodenplättchen („pads“) oder als Lage von gespannten Drähten ausgeführt sein. MP-41 Teil 2: Physik exotischer Kerne, SS-2012 3.2 Zeitprojektionskammer TPC Prinzip: Time Projection Chamber (TPC) basieren auf der Drift der Ladungsträger mit konstanter Driftgeschwindigkeit vD in einem homogenen E-Feld (E = -dV/dz). - typische Parameter: E ~ 1 kV/cm, vD ~ 1-4 cm/μs, Δz ~ 200 μm - 3-dim. Spuren: z aus Driftzeit, (x,y) aus segmentierter Anode MP-41 Teil 2: Physik exotischer Kerne, SS-2012 4. Szintillationsdetektoren Szintillationsdetektoren konvertieren γ-Strahlung und die durch ionisierende Teilchen erzeugte Anregung im Festkörper in sichtbares Licht, Nachweis durch Photomultiplier, Photodioden. anorganische Szintillatoren Material: NaJ, CsJ, BGO (Bi4Ge3O12) Kristalle, die mit Aktivator-Zentren (Farbzentren) dotiert sind. - hohe Lichtausbeute (bis zu 50000 Photonen/MeV) - lange Abklingzeiten (250 – 1000 ns) Strahlungslänge X0 ist eine material-abhängige Größe, die angibt nach welcher Strecke die Energie eines relativistischen Elektrons auf 1/e abgefallen ist. MP-41 Teil 2: Physik exotischer Kerne, SS-2012 4. Szintillationsdetektoren Organische Szintillatoren: Plastik-Szintillatoren Anorganische Szintillatoren: NaI, CsI, BaF2, BGO Bei Szintillatoren handelt es sich um Materialien in denen die einfallende Strahlung Elektronen in energetisch höhere Zustände anregt, die durch Emission von Licht abgeregt werden. (mittlerer Energieverlust, welcher zur Erzeugung eines Photons nötig ist: Anthracen C14H10 60eV, Plastik 100 eV, NaI 25 eV, BGO 300 eV) MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Szintillator-Lichtleiter-Photomultiplier Lichtleiter: Photomultiplier sind oft über Lichtleiter an den Szintillator gekoppelt. Grundprinzip: Totalreflektion an der Oberfläche des Lichtleiters Effizienz des Lichtleiters wird limitiert durch Winkel für Totalreflexion. Szintillatorplatte mitangeklebtem PMMA-Lichtleiter und einer Eichquelle für ein Gammastrahlen-Experiment. MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Photovervielfacher-Röhren Umwandlung von Licht in elektrisches Signal. Quanteneffizienz einer typischen Photokathode: 30% Nachweis von Szintillationsund Tscherenkow-Licht MP-41 Teil 2: Physik exotischer Kerne, SS-2012 Teilchendetektoren Wenn ein geladenes Teilchen in einem Szintillator Energie verliert, geschieht dies meist durch Anregung der Atome bzw. Moleküle des Szintillators. Ein Großteil der angeregten Elektronen gibt beim Übergang ins Grundniveau diese Energie über strahlungslose Rotationund Vibrationsübergänge an die Umgebung ab. Nur wenige Prozent emittieren ein Photon im sichtbaren oder nahen UltraviolettBereich. In Plastikszintillatoren wird im Mittel ein Photon pro 100eV Energieverlust emittiert. Für eine bestimmte Szintillatorgeometrie erreichen nur 6% dieser Photonen die Photokathode des Photomultipliers, mit dem sie nachgewiesen werden, der Rest wird im Szintillator oder den Wänden absorbiert. Die Photokathode hat eine Quantenausbeute von 30%, d.h. nur 30% der auftreffenden Photonen erzeugen ein Photoelektron, das im Photomultiplier verstärkt wird. In einem Argon-gefüllten Gaszählrohr werden 25eV pro Ionisierung gebraucht. In einem Halbleiterdetektor wird im Mittel eine Energie von 3.6eV (Si) benötigt, um ein Elektron-Loch-Paar zu erzeugen. Für die beiden letzten Detektoren nehmen wir an, dass 100% der Ladungsträger nachgewiesen werden. Wie groß ist der statistische Anteil der relativen Energieaullösung σE/E eines Detektors für einen Energieverlust des Teilchens von 100keV, %MeV und 20MeV? Berechnen Sie die Anzahl der nachgewiesenen Photonen, Ionisationen und Elektron-Loch-Paare. Gehen Sie bei der Berechnung von einer Poissonverteilung aus. In der Poisson-Statistik ist der Fehler einer Zählrate N gleich der Wurzel der Zählrate N N . Der relative Fehler wird dadurch E N 1 E N N Prozess ΔE (MeV) EProzess(eV) N ΔN σ(ΔE)/ΔE Szintillator 0.1 100 / 0.018 18 4.2 0.236 0.024 5 =5556 900 30 0.033 0.167 20 3600 60 0.017 0.333 0.1 2.78·104 167 0.006 0.0006 1.39·106 1179 0.0008 0.0042 20 5.56·106 2357 0.0004 0.0085 0.1 4·103 63 0.016 0.0016 2·105 447 0.0022 0.011 8·105 894 0.0011 0.022 Halbleiter 5 Gaszähler 5 20 3.6 25 MP-41 Teil 2: Physik exotischer Kerne, SS-2012 σ(ΔE) (MeV)