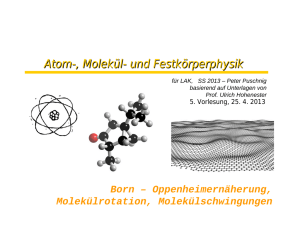
Sternentstehung: Entstehung von Doppelsternen

Sternentstehung: Entstehung von Doppelsternen
Klumpen in Molekülwolken
• Molekülwolken zeigen eine klumpige Unterstruktur
• Die Massenverteilung der Klumpen folgt einem Potenzgesetz:
N(m) ∼ m −2
• Sterne bilden sich in Sternhaufen, die
diesem Potenzgesetz folgen
Die Klumpen sind die
Gebiete aus denen
Sternhaufen entstehen.
Im Gegensatz zu dichten Gasklumpen
ist die stellare Massenfunktion nicht
skalenfrei.
Molekulare Kerne
1.3mm Staubkontinuum Beobachtungen mit dem IRAM 30m
Radioteleskop zeigen sehr dichte Gasgebiete: molekulare Kerne.
• Cluster von Kernen
in Klumpen
• Kohärente, gebundene
Strukturen
• Geringe Linienbreiten
σ
cs
≈ 0.7
Molekulare Kerne
1.3mm Staubkontinuum Beobachtungen mit dem IRAM 30m
Radioteleskop zeigen sehr dichte Gasgebiete: molekulare Kerne.
• Cluster von Kernen
in Klumpen
• Kohärente, gebundene
Strukturen
• Geringe Linienbreiten
σ
cs
≈ 0.7
Eigenschaften von molekularen Kernen:
• Gravitativ gebunden
• Die Massenverteilung entspricht der
stellaren Massenverteilung.
• Kerne haben sich von der turbulenten
Gasbewegung entkoppelt
*
Kerne
Numerische Simulation der Fragmentation
und Sternentstehung
(Klessen & Burkert, 1998, 2000, 2001)
Massenfunktion der Sterne
Simulation
Beobachtung
Das Drehimpulsproblem I
Protostellare Kerne kollabieren innerhalb von 1 − 2 ⋅105 Jahren .
Aber die Kerne rotieren mit
dvlos
≈ 1 − 10 km / s / pc
dr
vlos = Ω ⋅ r
Ω ≈ 3 ⋅10−14 − 3⋅10−13 s −1
Spitzers Problem (78):
(Goodman et al. 93)
0.3 pc = 1018 cm
Ein protostellarer Kern:
M ≈ 1M ⊙
Ω ≈ 3 ⋅10−14 s −1
Während des Kollapses auf Sterngröße von 6 ⋅1010 cm
führt die Drehimpulserhaltung zu Winkelgeschwindigkeiten von:
Ω ⋅ R 2 erhalten → Ωfinal ≈ 0.1s −1
Der Stern würden dann an seiner Oberfläche mit 20% der
Lichtgeschwindigkeit rotieren, d.h. 104 mal der kritischen
Rotation.
Beobachtungen: Sterne rotieren mit ~10% des kritischen Wertes
Der protostellare Kollaps führt zur Bildung von Scheiben.
Das Drehimpulsproblem II
Charakteristische Werte des spez. Drehimpulses (Bodenheimer 95):
Molekülwolken:
1023 cm 2 s −1
Molekulare Kerne:
1021 cm 2 s −1
100 AU Scheibe:
Anfang
5 ⋅1020 cm 2 s −1
Ende
T Tauri Stern (Spin):
5 ⋅1017 cm 2 s −1
Die Scheiben enthalten nur 10% der Masse des Sterns: die
Drehimpulsverteilung j(m) ist am Ende anders als am Anfang.
Doppelsterne
(P = 104 yr ⇔ 5 ⋅1020 cm 2s −1 )
Kollaps einer homogenen Spähre
Scheibenentstehung
Akkretionsschock
Fragmentation der Scheibe
Kollaps eines homogenen Kerns mit einer 50% m=2 Störung
(Boss & Bodenheimer 79; Burkert & Bodenheimer 93)
ρ = ρ0 [1 + 0.5cos ( 2ϕ )]
hohe Dichte
Expansion
Doppelstern
10% m=2 Störung (Burkert & Bodenheimer 93):
vertikale Scheibenstruktur
fragmentierendes Filament
Fragmentation von zentral kondensierten Kernen
ρ(r) = ρ0 exp(− r 2 / r02 )
ρ0 = 20 ⋅ρ(R max )
10% m = 2 Störung