P. Reiter - User web pages on web

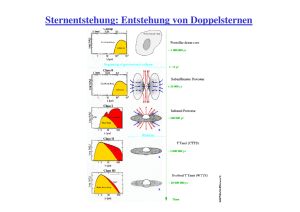
Kernphysik I
Kernmodelle:
• Vibrationsanregungen
• γ-Zerfall
Wiederholung: Deformierte Kerne
Nilsson Zustände
Zur Charakterisierung der Zustände werden
die asymptotische Quantenzahlen
[NnzΛ Ωπ] oder Ωπ [NnzΛ] verwendet.
(Definition kommt gleich)
Nur für große Deformationen β2, δ
sind [NnzΛ] Konstanten der Bewegung.
Bei großer Deformation, kann man die
Bewegung eines Nukleons im deformierten
Potential trennen in Komponenten
entlang und senkrecht zu der Deformationsachse,
die bei axial symmetrischer Deformation als Quantisierungsachse dienen kann.
Die Entartung der Zustände mit bestimmten j, wird hinsichtlich ihrer Projektion m
auf die Deformationsachse aufgehoben, Zustände mit ±m bleiben entartet.
Beispiel: j = 5/2 spaltet in 3 Komponenten auf mit |m|= 5/2; 3/2; 1/2
Wiederholung: Kollektive Kernanregungen
Die Anregung von Einteilchenzuständen
ist auf Kerne in der Nähe abgeschlossener
Schalen beschränkt. Bei allen Kernen
(außer den sehr leichten) ist die Anregung
kollektiver Freiheitsgrade möglich.
Kerne mit vielen Nukleonen außerhalb
abgeschlossener Schalen zeigen auch
kollektive Anregungsspektren.
Kollektive Kernanregungen sind
Fluktuationen des Kerns um die
Gleichgewichtslage:
Dichtefluktuationen oder
Formfluktuationen
Experimentelle Untersuchung:
Kollektive Anregungen werden am
besten mit Hilfe elektromagnetischer
Übergänge untersucht, d.h. mit
γ-Spektroskopie
Beobachtete kollektive Kernanregungen:
• Rotationszustände deformierter Kerne
• Vibrationszustände
Quadrupolschwingungen
Oktupolschwingungen
• Riesenresonanzen
Dipolriesenresonanz
Analogie in der Molekülphysik:
• Einteilchenanregung
• Vibration
• Rotation
Informationen über den Charakter der
Anregung erhält man aus:
• Systematik der Anregungsenergien
• Übergangswahrscheinlichkeiten
• γ-Winkelverteilung
Formschwingungen
Einfachsten Formschwingungen:
- Quadrupolschwingungen
- Oktupolschwingungen
Beobachtung:
Alle gg-Kerne haben im Grundzustand
Spin und Parität Jπ=0+ und - bis auf die
doppelt magischen Kerne - im ersten
angeregten Zustand Jπ=2+
Die Übergangswahrscheinlichkeit
für diese E2-Anregung zwischen
0+ und 2+ ist um bis zwei Größenordnungen höher als für Einteilchenübergänge.
Kollektive Vibrationsanregung
Vibrationszustände
Mittlere
Form
momentane
Form
Oberflächenschwingungen
R(t) = R avr + ∑
Instantane
Koordinate
λ=0
Monopol
r0A1/3
λ
∑α
λμ
(t) Yλμ (θ, φ)
α λμ = α λ, -μ
Symmetrie
λ μ = − λ Amplitude
Sphärische
Kugeloberflächenfunktionen
λ=1
Dipol
λ=2
Quadrupol
λ=3
Oktupol
.
Monopol und Dipol-Anregung
benötigen hohe Anregungsenergie.
Oberflächenschwingungen
R(t) = R avr +
2
∑ α 2μ Y2μ (θ ,φ )
μ = −2
λ=2
Quadrupol
= R avr + α 22 Y22 + α 21 Y21 + α 20 Y20 + α 2,-1Y2,-1 + α 2, -2 Y2, -2
= R avr + α 20 Y20
• Quantisierung der Quadrupol-Vibration nennt man
Quadrupol-Phonon.
• Ein Phonon trägt zwei Einheiten des Drehimpulses.
• Diese Anregungsmode ist dominant.
• Für die meisten gg Kerne existiert ein niedrig liegender
Zustand mit Jπ=2+. Entweder von kollektiver Rotation oder
Vibration.
Formschwingungen
β - Vibration
γ - Vibration
Formschwingungen
Oktupolschwingungen
In doppelt magischen Kernen (16O, 40Ca, 208Pb)
wird niedrig liegender 3--Zustand beobachtet.
Zustände haben um bis zu zwei Größenordnungen
höhere Übergangswahrscheinlichkeiten als
Einteilchenübergänge.
Die kollektiven 3--Zustände können als Oktupolschwingungen interpretiert werden.
Können als kohärente Überlagerung von TeilchenLoch-Zuständen zwischen benachbarten Schalen
erzeugt werden.
Anders als bei der Dipolriesenresonanz ist hier die Schwingung von
Protonen und Neutronen gleichphasig. Dadurch ist die Teilchen-LochWechselwirkung anziehend und die kollektive Oktupolanregung in der
Energie nach unten verschoben.
Elektromagnetische Übergänge
Die Übergangswahrscheinlichkeit vom
Zustand i in den Zustand f ergibt sich
nach Fermis Goldener Regel zu:
2π
dW =
ψ f H int ψ i
h
2
dρ ( E ) =
(2πhc )3
A = (φ / c, A)
⋅ dρ ( E )
Der Phasenraumfaktor für die Emission
eines Photons mit der Energie Eγ in das
Raumwinkelelement dΩ ist gegeben:
Eγ2V dΩ
WW eines geladenen Teilchens mit dem
elektromagnetischem Feld
Die Energie eines geladenen Teilchens
v
im EM Feld:
ist klassisch gegeben durch:
v2
1 v
(
H =
p − eA) + eφ
2m
v
p2 e v v
H =
− pA + e φ
2m m
Wechselwirkungsterm:
H int
e vv
= − pA + e φ ≡ j ⋅ A
m
mit elektrischem Viererstrom j und
EM-Feld A.
Photonen haben transversale Polarisation
-> keine Monopolübergänge, eφ trägt nicht bei.
Elektromagnetische Übergänge
Quantenmechanisch:
ersetze Impuls
v
v
v
p → − i h ∇ A ≡ Wellenfunktion des Photons
Matrixelement:
ψ f H int ψ i
v
v
ieh
3
*
=−
d rψ f ( ∇ ψ i ) A
∫
m
Vertauschungsrelation:
v
ih v h2 v
[r , H 0 ] = p = ∇
m
m
Umformung:
ψ f H int ψ i
v
ie
3
*v
= ( E i − E f ) ∫ d rψ f r ψ i A
m
Matrixelement für Multipolstrahlung
Photon wird durch ebene Welle dargestellt:
v
A=
h
2ε 0ωV
vv
ε cos( kr − ω t )
mit dem Polarisationsvektor ε
der Energie Eγ = ħω
und dem Wellenvektor k
Elektromagnetische Übergänge
Für die Übergangswahrscheinlichkeit gilt damit:
vv
2
e2
3 v
3
* v ikr
dWfi =
E γ ε ∫ d rψ f re ψ i d Ω
2
4 3
8π ε 0 h c
mit Eγ ~ MeV ist λγ >> RKern und
man entwickelt exp(ikr) nach Multipolen:
e
vv
ikr
vv
= 1 + ikr + ....
Elektrische Dipolübergänge (E1)
Aus eikr=1 folgt die Dipolübergangswahrscheinlichkeit
z.B. für γ-Zerfälle bei Einteilchenanregung oder kollektiven
Anregungen.
( E 1)
W fi
e2
3
3
*v
E γ ∫ d rψ f r ψ i
= = λ (E1) =
4 3
3πε 0 h c
τ
1
W fi( E 1) ∝ E γ3
2
Höhere Multipole Übergangsmatrixelement
Abschätzung mit “einfachen” Näherungen für
Übergang zwischen zwei Protonen-Einteilcheniveaus:
ψ i = Rnl' (r )ϕ j ' l' m' (θ, φ )
ψ f = Rnl" (r )ϕ j "l"m" (θ, φ )
Annahme: R n l ' (r ) ~ konstant
für 0 ≤ r ≤ R
Allgemein gilt:
Mittelung über Anfangszustände m’
Summierung über die Endzustände m”.
R = Ro A1/ 3
2l+1
2
⎛
⎞
E
π
l
+
1
⎛
8
⎞
(
)
e
3
γ
2l
λE (l,m ) =
cR
⎜
⎟
⎜ ⎟
⎝ l + 3⎠
hl(2l + 1)!! 4 πεo hc ⎝ hc ⎠
2
2l+1
2
⎞
⎛
⎞
E
8
π
l
+
1
⎛
⎛
⎞
⎞
(
)
e
h
3
1
γ
2l−2
λM (l,m ) =
⎟⎜ ⎟
⎜μ p −
⎜
⎟ ⎜
⎟ cR
⎝l + 2⎠
l + 1⎠ ⎝ m p c ⎠⎝ hc ⎠
hl(2l + 1)!! 4 πεo hc ⎝
2
2⎛
Übergangswahrscheinlichkeit für γ-Zerfälle
Resultate für Einteilchen-Proton-Übergänge:
λE (l = 1) = 1.0 ×1014 A 2 / 3 E 3
λM (l = 1) = 5.6 ×1013 E 3
λE (l = 2) = 7.3 ×10 7 A 4 / 3 E 5
λM (l = 2) = 3.5 ×10 7 A 2 / 3 E 5
λE (l = 3) = 34 A 2 E 7
λM (l = 3) = 16A 4 / 3 E 7
λE (l = 4 ) = 1.1 ×10 −5 A8 / 3 E 9
λM (l = 4 ) = 4.5 ×10 −6 A 2 E 9
Wichtige Verhältnisse:
λ (l + 1)
≈ 10 −5
λ (l)
λE (l)
2
≈
10
λM (l)
Multipolstrahlung besitzt Drehimpuls l und definierte Parität:
π l = ( -1)
(l)
π l = ( -1)
( l +1)
Elektrische Multipolstrahlung
Magnetische Multipolstrahlung
Auswahlregeln für γ-Übergänge
Für die E-M Wechselwirkung
gelten die Erhaltungsgrößen:
-Energie
r
r
-Impuls
E
,
p
,
L
-Drehimpuls
-Parität
Betrachte den Übergang:
, π
Ii → If + L γ
Auswahlregeln
Drehimpuls
Parität
Beispiele:
Ii − If ≤ Lγ ≤ Ii + If
m = mi − mf
πi = πf ⋅πγ
Ii = 3 +
If = 2 −
Ii = 0+ → If = 0+ + Lγ