(+1) = (+1)

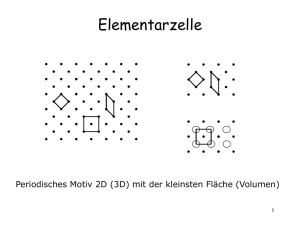
Symmetrielehre - Beispiele
Literatur
- J. E. Huheey, E. A. Kreiter, R.L. Kreiter Anorganische Chemie,
de Gruyter 1995
- F. Engelke Aufbau der Moleküle, Teubner 1996
- R.L. Carter Molecular Symmetry and Group Theory, Wiley 1998
- S.F.A. Kettle Symmetrie und Struktur, Teubner 1994
- D.C. Harris, M.D. Bertolucci Symmetry and Spectroscopy,
Dover 1989
- D.M. Bishop Group Theory and Chemistry, Dover 1973
- F.A. Cotton Chemical Applications of Group Theory,3ed
Wiley 1990
Symmetrielehre - Anwendung & Nutzen!
· IR, UV/VIS-Spektroskopie - Auswahlregeln (Bandenzahl)
· NMR-Spektroskopie - Anzahl Resonanzen
· MO-Theorie - Wechselwirkungsdiagramme
· Kristallographie - Strukturanalyse
(zusätzliche Symmetrieoperation: Translation..)
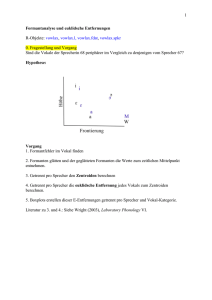
Symmetrielehre
empirisch: Körper zeigen unterschiedliche Symmetrieeigenschaften
180°
Kugel
Würfel
Jede Rotation um Achse bringt Kugel
wieder auf Deckung mit sich selbst
120°
90°
Ausgewählte Symmetrieelemente
des Würfels (Rotationsachsen)
 geringere Symmetrie als Kugel
Systematische Behandlung: Gruppentheorie
Symmetrie
Symmetrieoperationen:
Zu jeder Symmetrieoperation gibt es ein zugehöriges Symmetrieelement
zusätzlich noch weitere Symmetrieoperationen
Symmetrieoperation: Identität
Symbol E: "macht gar nichts!"
entspricht Drehung um 360° oder 0°
- notwendig für vollständige Beschreibung innerhalb
der Gruppentheorie
E =neutrales Element
Symmetrieoperation - Rotation
· H2O hat eine zweizählige Achse
 C2-Achse 360°/2 = 180°
Atome kommen bei Drehung um 180°
wieder zur Deckung
· NH3 hat eine dreizählige Achse
 C3-Achse 360°/3 = 120° (360/n)
Atome kommen bei Drehung um 120° (C3)
und 240° wieder zur Deckung
ebenso: C4, C5, C6 .. Cn-Achsen
 Hauptachse: Achse höchster Zähligkeit: z-Achse
Symmetrieoperation - Rotation
C41
C4
-90°
+90°
C34 = C41
C34
+270°
C2 +180°
C24 +180°
m
allgemein: C n
Bezeichnung: C2
Drehung um: m·360°/n
2
z.B. 2·360°/4=180° = C4
Bezeichnung der Drehachsen
z
C4 /C2
2+
OC
OC
C2 ´
Pt
CO
C2´´
CO
C2´´
Hauptdrehachse: C4  z-Achse
C2 ´
Koordinatensystem
- Ursprung Zentralatom z.B. CH4 C-Atom
- Drehachse höchster Zähligkeit z-Achse
tetraedrische Moleküle x,y,z Achsen colinear mit C2-Achsen
z
- planare Moleküle
y
z-Achse ^ auf Molekülebene
F
F
x-Achse beinhaltet größte Atomzahl
Xe
F
F
z
x
wenn z-Achse in Ebene, dann x ^ auf Molekülebene
x
z
- rechtshändiges Koordinatensystem
H
y
x
y
O
H
Spiegelebene
• Wasser 2 Spiegelebenen
• stehen senkrecht aufeinander
v and v‘
• beinhalten Hauptdrehachse
(hier C2-Achse)
Symmetrieelement: Ebene
Symmetrieoperation: Spiegelung
Dihedrale Spiegelebenen
c6-Hauptachse
c2-Achse
c2-Achse
d
c6
(z-Achse)
c2-Achse
d
d
• dihedrale Spiegelebenen d schneiden C2-Achsen
senkrecht zur Hauptachse
Horizontale Spiegelebene
2Cl
Cl
h
Pt
Cl
Cl
h
h
Cl
Cl
2-
Pt
Cl
Cl
dz2-Orbital symmetrisch
-Orbital antisymmetrisch
Inversionszentrum
i
Inversionszentrum i
Oktaeder
i
Ethen
W(CO)6
Symmetrieoperation:Drehspiegelachse
Kombination aus Drehachse und Spiegelung an Ebene ^ auf Drehachse
Bezeichnung: Kombination aus C4-Achse und Spiegelebene 
S4-Drehspiegelachse
z.B. Methan hat eine Drehspiegelachse (S4):
C4

C2, S4
X
X
Tetraeder 3 S4-Achsen
M
C2, S4
X
C2, S4
X
Symmetrieoperation:Drehspiegelachse
C4
C
C
C
C
C
C
C
v
Allen
C
C
S4-Achse
NB: S2-Achse: C2 &  = i (Inversionszentrum)
y
x
x
z
C2
x,y,z
z
= Inversion
x

z
y
-x,-y,z
y
-x,-y,-z
Definition von Spiegelebenen: h, d, v
C6
S6-Drehspiegelachse
H
H
H 60°
H
H
H

Newman Projektion
Ethan
H
H
H
H
H
H
Symmetrie & Chiralität
Br
I) asymmetrisch = chiral - nur Identität E
F
Cl
I
Me
II) dissymmetrisch = chiral - nur Cn-Achsen
C2
Me
I) & II) identische skalare aber unterschiedliche vektorielle Eigenschaften
z.B. Sdpkt. (skalar)
Wechselwirkung mit polarisiertem Licht (vektoriell)
Me
III) symmetrisch = achiral i, Sn, 

Me
identische skalare und vektorielle Eigenschaften
NMR-Spektroskopie
Me
homotope Protonen (Kerne) Cn-Achsen
C2
Me
gleiche chemische Verschiebung unabhängig vom Lösungsmittel
CH3
enantiotope Protonen (Kerne) 

CH3
gleiche chemische Verschiebung in achiralem Lösungsmittel
kann in chiralem Lösungsmittel unterschiedlich sein
Me
diastereotope Protonen (Kerne)
keine Symmetrie
chemische Verschiebung kann in a/chiralem Lösungsmittel
unterschiedlich sein (kann zufällig gleich sein)
CH3
CH3
NMR-Spektroskopie
wichtig hierbei: Zunächst auf Homotopie überprüfen!
CH3
CH3

C2
CH3
C2
H
H
CH3
H
H
H
H
H
H
H
homotop! 1 Resonanz!
C2
C2
H
homotop!
H
koppeln nicht!
H
CH3
H
H
H
H
CH3
CH3
1H-NMR-Spektrum
CH3
6H
4H
7
 ppm
2
kombinierte Symmetrieoperationen  Gruppentheorie
C2
Br b
[E]
Bra
 Bra   Bra 
 Br   Br 
 b =  b
Cla  Cla 
   
Cl b  Cl b 
[
 Bra   Brb 
 Br   Br 
 b =  a 
v] Cla  Cla 

 

Cl b  Cl b 
C
Clb
Cl a
v
v'
 Bra   Brb 
 Br   Br 
[C2]Clb  = Cla 
a
b

 

Cl
Cl
 b  a 
[
 Bra   Bra 
 Br   Br 
 b =  b
]
v‘ Cl  Cl 
a
b

 

Cl
Cl
 b  a 
Matrixschreibweise:
Aussehen der [E], [C2], [v], [v.]-Matrizen später
Kombinationen von Symmetrieoperationen:
EE = E C2C2 = E
vv= E v‘v‘ = E
EC2 = E Ev = v
Ev‘ = v‘

  Brb   Bra 
 Bra  
 Bra 




 Br 
 Br 
Br 
 Br 




b
a
b
b
[C2 ]x  [ v ]x    = [C2 ]x     =   = [ v ' ] 
Cla 
Cla 
Cl b 
Clb 




2.  1.   
 
 Cl   Cl 
Cl
Cla 
 b

  b  a 
Kombinierte Symmetrieoperationen

 Bra  
 Bra 


 Br 
 Br 


b
b
[C2 ] x  [ v ] x    = [ v ' ] 
Cla 
Cla 


2.  1. Cl  
 
 b 
Clb 


 Bra  
 Bra 


 Br 
 Br 


b
b
[ v ] x  [C2 ] x    = [ v ' ] 
Cla 
Cla 


2.  1. Cl  
 
 b 
Clb 

hier: C2v = vC2
kommutativ nicht allgemeingültig!
Ergebnis meist abhängig von der
Reihenfolge der Symmetrieoperation
z.B. S4 x v v x S4
Beispiel nicht-kommutativ:
D
C
S4
A
v
B
C
B
D
D
A
A
C
B
v
S4
C
D
B
A
C2
A
B
D
C
S4 x v v x S4
Symmetrieoperationen - Multiplikationstafel
1.
2.
E
C2
v
v'
E
E
C2
v
v'
C2
C2
E
v'
v
v
v
v'
E
C2
v'
v'
v
C2
E
Lesart zunächst Zeilen- dann Spaltenoperation
(hier allerdings irrelevant da kommutativ)
v x C2 =v‘
etwas Mathematik - Gruppentheorie & -axiome
Eine Menge G von (mathematischen) Elementen A, B, C heißt Gruppe,
wenn die folgenden 4 Axiome erfüllt sind:
Elemente (mathematischer Sinn): {E, C2, v, v´G}
Axiom 1: Verknüpfung o zwischen den Elementen A,B ({A,B G})
führt zu einer eindeutigen Zuordnung:
C = AoB
wobei {C G} Vollständigkeit
vgl.: Multiplikationstafel
von CH2Br2 Beispiel
E C2 v v'
E E C2 v v'
C2 C2 E v' v
v v v' E C2
v' v' v C2 E
z.B. v´= C2ov
{v´G}
etwas Mathematik - Gruppentheorie & -axiome
Axiom 2: Die Verknüpfung o erfüllt das Assoziativgesetz:
(AoB)oC=Ao(BoC)
CH2Br2 Beispiel:
E C2 v v'
E E C2 v v'
C2 C2 E v' v
v v v' E C2
v' v' v C2 E
C2o(vov´)= C2oC2=E
C2
(C2ov)ov´= v´ov´=E
v´
C2o(vov´)=(C2ov)ov´
Assoziativgesetz erfüllt
etwas Mathematik - Gruppentheorie & -axiome
Axiom 3: Existenz eines neutralen Elementes für alle Elemente von G.
EoA = AoE = A
CH2Br2 Beispiel:
EoC2 = C2oE = C2
Axiom 4: Existenz eines inversen Elementes für alle Elemente von G.
AoA-1 = A-1oA =E
CH2Br2 Beispiel:
E C2 v v'
E E C2 v v'
C2 C2 E v' v
v v v' E C2
v' v' v C2 E
EoE =
C2oC2 =
vov =
v´ov´ =
E
E
E
E
etwas Mathematik - Gruppentheorie & -axiome
zusätzlich - kein Kriterium für eine Gruppe:
wenn sämtliche binäre Operationen kommutieren Abel´sche Gruppe
AoB = AoB
CH2Br2 Beispiel: hier erfüllt!
E C2 v v'
E E C2 v v'
C2 C2 E v' v
v v v' E C2
v' v' v C2 E
voC2 = C2ov
sowie für alle weiteren Kombinationen!
(= symmetrische Matrix i.a. eher Ausnahme)
Abel´sche Gruppe
Symbol der Punktgruppe C2v
S6-Drehspiegelachse
H
H
H 60°
H
H
H

Newman Projektion
Ethan
H
H
H
H
H
H
Diagramm zur Bestimmung der Punktgruppe nach Schönflies
Molekül
ja
Dh
F
l
u
ja linear? nein
ß
d
i?
ja 2 oder mehr nein
i
Cn, n > 2 ?
a
nein
g
ja
r
i?
Flußdiagramm 2 a
ja
m
C5 ? nein
m
1
Cv
Ih
Oh
Td
lineare Gruppen
z.B
C60
kubische Gruppen
von Flußdiagramm 1
Cn? N
J
J  ?N
h
J ? N
J n C2´s ^Cn ?
n2
N
 ?J
J i?N
h
N
n d ?
J
N
n v ?
N
J
S2n ?
N
Dnh
Dnd
Dn
Cn
S2n
Cnv Cnh
Cs
Ci
C1
F
l
u
ß
d
i
a
g
r
a
m
m
2
Ordnung
1
2
2
assymetrisch
zyklische Gruppe
n
2n
2n
2n
2n
4n
4n
dissymetrisch
Diedergruppe
dissymetrisch
kubische Gruppe
24
48
120
Ordnung: Gesamtzahl der Symmetrieoperationen
z.B. C2v: n =2
Ordnung=4
Kubische Gruppen
Tetraeder
Oktaeder
Ikosaeder
Ikosaeder
Dodekaeder
Td-Symmetrie
C2, S4
C3-Achsen
X
X
X
M
C2, S4
M
C2, S4
X
X
X
C3
X
Beispiele für Punktgruppen
O
S
C1
F
Ph
Me
F
I
C4v
Cl
Cl
N
B
Cl
CS
F
F
Br
H
Br
Cl
Ci
C2
Br
O
N
F
H
F
N
O
B
C3h
C2h
Cl
H
H
C3v
H
F
F
B
O
F
H
D3h
F
Fe
Fe
Co
F
F
Co
F
D5h
D5d
D3
chiral!
F
F
Oh
C60 Ih
Punktgruppenbestimmung Ferrocen ekliptisch
N
Y
1)
Fe
C5
Y
C5
Y
2)
C2
Fe
=
C2
D5h
3)
Fe h
D5h
Klasse von Symmetrieoperationen
B = X-1AX Ähnlichkeitstransformation:
B und A zueinander konjugiert
C3v
E
C31
C32
v
 v'
 v"
E
E
C31
C32
v
 v'
 v"
C31
C31
C32
E
 v'
 v"
v
C32
C32
E
C31
 v"
v
 v'
C32vC31 = C32v’ = v”
C32C31C31
= C31
vC31v
= C32
v
v
 v"
 v'
E
C32
C31
 v'
 v'
v
 v"
C31
E
C32
 v”
 v"
 v'
v
C32
C32
E
N
H
C3v
EC31E
= C31
C31C31C32 = C31
v'C31v' = C32
Zur Erinnerung: C32=C31,-1 v=v-1
H
H
Resultat: C32vC31 immer v, v’ oder v”
 v’
v’’
jedoch nie E, C31 or C32.
v, v’ and v” sind in der gleichen KLASSE.
Gleiches gilt für X-1EX = E
sowie
X-1 C31 X und X-1 C32 X = C31 or C32
für alle X der Gruppe.
Punktgruppe C3v: 6 Symmetrieoperationen
E
C31, C32
3 Klassen
v, v’ , v”
Zur Bedeutung später!
vorneweg: Anzahl Klassen = Anzahl irreduzibler Darstellung
Darstellung der Gruppen - Charaktertafeln
Schemata zur Darstellung der Effekte von Symmetrieoperationen
auf Moleküle sind sehr aufwendig.
C4
z.B.

Bevorzugt: numerische Darstellung der Effekte
Alternative: Zuordnung/Verwendung von Vektoren
Auswirkung der Sym-Ops auf Vektoren  numerisch
Beispiel : SO2 (dreitomig, C2v-Symmetrie)
z
y
S
x
z
x
O
z
y
x
y
O
y
Große Pfeile in y-Richtung Translation
& -vektor, Ty
C2v-Symmetrie: Sym-Ops: E, C2, xz and yz.
ETy=Ty
yTy=Ty
keine Änderung Symbol +1
C2 and xz  Vorzeichenumkehr
numerisches Symbol -1.
S
O
O
C2 rotation
S
O
O
E(Ty) = (+1)(Ty)
C2(Ty) = (-1)(Ty)
xz(Ty) = (-1)(Ty)
yz(Ty) = (+1)(Ty)
Ty: BASISVEKTOR
±1 numerische Darstellung des Einflusses der Sym-Ops auf Ty
Analog: Tx und Tz Vektoren.
ebenso: ROTATIONSVEKTOREN
z
x
y
S
O
z
x
O
S
O
z
y
x
O
y
Blick entlang z-Achse
Rotationsvektor um z-Achse: Rz = Basisvektor.
E(Rz) = (+1)(Rz)
C2(Rz) = (+1)(Rz)
xz(Rz) = (-1)(Rz)
yz(Rz) = (-1)(Rz)
Analog: Rx, Ry und Tx und Tz-Vektoren:
C2v
E
C2
xz
yz
+1
+1
+1
+1
+1
+1
-1
-1
+1
-1
+1
-1
+1
-1
-1
+1
Tz
Rz
Tx, Ry
Ty, Rx
korrekte Darstellung der Punktgruppe C2v?
Beleg durch Überprüfung der Multiplikationstafel
C2v Multiplikationstafel:
xz yz = C2
C2v
E
C2
xz
yz
E
C2
xz
yz
+1
+1
+1
+1
+1
+1
-1
-1
+1
-1
+1
-1
+1
-1
-1
+1
Tz Darstellung :
(+1)(+1)
Rz Darstellung :
(-1)(-1)
Tx/Ry Darstellung : (+1)(-1)
Ty/Rx Darstellung : (-1)(+1)
Multiplikationstafel erfüllt:
= (+1)
= (+1)
= (-1)
= (-1)
Tz
Rz
Tx, Ry
Ty, Rx
Weiteres Beispiel: NH3 in C3v-Symmetrie
z
y
x
N
H
H
H
Translation in x und y-Richtung
y
H
Ty
N
H
Tx
H
x
Rotation von Tx and Ty um 120o (C3-Achse)
Ty
Ty
H
120o
N
TTxx''
H
H
TTxx
TTyy''
Zusammenhang zwischen "erzeugten" Vektoren, Tx' and Ty'
und den "alten" Vektoren Tx and Ty? (Basisvektoren)
Tx' = (cos 120o)Tx - (sin 120o)Ty = -(1/2)Tx - (3/2)Ty
Ty' = (sin 120o)Tx + (cos 120o)Ty= +(3/2)Tx - (1/2)Ty
Ty
cos(30o)Tx= (sin 120o)Tx
30o
(cos 120o)Ty
Tx
Ty'
Tx' = (cos 120o)Tx - (sin 120o)Ty = -(1/2)Tx - (3/2)Ty
Ty' = (sin 120o)Tx + (cos 120o)Ty= +(3/2)Tx - (1/2)Ty
Tx und Ty "mischen"  können nicht voneinander separiert werden!
Schreibt man besser als Matrix
[T '
x
 [
Ty ' = Tx
  (1 / 2)  ( 3 / 2)
Ty 


(
3
/
2
)

(
1
/
2
)



Matrizen - etwas Auffrischung
Matrizenmultiplikation: X·Y=Z
 x11 x12 
 y11 y12
x

x 22 
 21
  y 21 y 22
x 31 x 32 
 z11 z12 z13 
y13  

=
z
z
z
21
22
23 
y 23  
z 31 z 32 z 33 
Regel: "i-te Zeile mal j-te Spalte"
z11 = x11 y11  x12 y21
z12 = x11 y12  x12 y22
z13 = x11 y13  x12 y23
z21 = x21 y11  x22 y21
z22 = x21 y12  x22 y22
z23 = x21 y13  x22 y23
Zeile
Spalte
z31 = x31 y11  x32 y21
z32 = x31 y12  x32 y22
z33 = x31 y13  x32 y23
Z: quadratische Matrix (Anzahl Zeilen = Anzahl Spalten)
c: Spur der Matrix = Summe der Diagonalelemente
c = z11 + z22 + z33
ab hier
  (1 / 2)  ( 3 / 2)


[Tx Ty  = [Tx Ty 


(

3
/
2
)

(
1
/
2
)


Für jede Symmetrieoperation der Punktgruppe C3v läßt sich eine
Matrix aufstellen.
 2 x 2 TRANSFORMATIONSMATRIZEN
 1 0
E 

0
1


 v 's
1 0 


0

1


  (1 / 2)  (  3 / 2) 
C 

 (  3 / 2)  (1 / 2) 
1
3
  ( 1 / 2)  (  3 / 2) 



(

3
/
2
)

(
1
/
2
)


  ( 1 / 2 )  (  3 / 2) 
C 23 

  (  3 / 2)  ( 1 / 2) 
  ( 1 / 2)  (  3 / 2) 



(

3
/
2
)

(
1
/
2
)


Tz und Rz Vektoren von NH3:
z
z
TTzz
H
y
N
N
x
x
H
H
N
H
Rz
H
H
y
H
Rz
H
H
H
Tz +1 für alle Symmetrieoperationen.
N
Rz +1 für E, C31, C32; -1 für 3 v's,
H
H
v
Rz
H
N
H
H
Rz
Rz, = -Rz
Darstellung der Translations- und Rotationsvektoren von NH3
E
C31
C32
v
v
v
Tz
+1
+1
+1
+1
+1
+1
Rz
+1
+1
+1
-1
-1
-1
(Tx,Ty)
oder
(Rx,Ry)
 1 0   (1 / 2 )  (  3 / 2 ) 


 
 0 1   (  3 / 2 )  (1 / 2 ) 
1 0 


 0  1
  (1 / 2 )  (  3 / 2 ) 


  (  3 / 2 )  (1 / 2 ) 
  (1 / 2 )  (  3 / 2 ) 


  (  3 / 2 )  (1 / 2 ) 
  (1 / 2 )  (  3 / 2 ) 


  (  3 / 2 )  (1 / 2 ) 
1x1 Vektoren = Zahlen
2x2 Vektor = Matrix
Darstellung der C3v-Punktgruppe (Vollständigkeit)?
 Beleg durch Matrizenmultiplikation/Multiplikationstafel
 erfüllt (ohne Beweis)
Translations- oder Rotationvektoren zur Erzeugung der Darstellungen
BASISVEKTOREN  Darstellungen
Wahl "beliebiger" BASISVEKTOREN, z.B. ORBITALE.
z.B. py Orbital von O-Atom von Wasser:
z
–
O
+
y
x
H
E
+1
C2
-1
H
xz
-1
yz
+1
py Orbital  gleiche Darstellung wie Ty Vektor.
dx2-y2-Orbital des Xe-Atoms von XeF4 Punktgruppe D4h :
x
F
+
F
– Xe –
+
F
Blick in Richtung C4-Achse
y
F
E
2C4
C2
2C2'
2C2"
i
2S4
h
2v
2d
dx2-y2 +1
-1
+1
+1
-1
+1
-1
+1
+1
-1
NB:
(1) 2C4 steht für C41 und C43; 2S4 für S41 und S43
(2) C2 = C42
(3) C2', v beinhaltet Xe-F Bdg.; C2", d schneidet F-Xe-F Winkel
px, py-Orbitale
F
px
–
– Xe +
+
F
F
y
C4
Py
F
x
Rotation um 90o (i.e. C41) transformiert px in –py, und py in px.
2 x 2 Transformationsmatrizen.
[p'
x
 [
p' y = p x
 0  1
py 


1
0



für C41
Weitere Symm-Ops in D4h-Symmetrie:
ebenfalls 2 x 2 Transformationsmatrizen für px, py
Atomorbitale als Basisfunktionen:
wichtige Regeln:
- s-Orbitale: kugelsymmetrisch
 +1 für alle Symmetrieoperationen
- 2 oder mehrere Orbitale, die durch Symmetrieoperationen
vertauschbar sind, müssen die gleiche Energie besitzen (entartet)!
 Symmetrieoperationen führen zu keiner Veränderung der Energie
Reduzible und Irreduzible Darstellungen
Bislang haben wir nur 1 oder 2 Vektoren als Darstellungen benutzt:
 "Freiwillige Selbstbeschränkung:" keine Grenze nach oben
Jede Darstellung mit n (unabhängigen) Vektoren/Funktionen
besteht aus n x n Matrizen.
unendliche Zahl von möglichen Darstellungen
Aber:!
Zerlegung in einige wenige (irreduzible) Darstellungen möglich!
Beispiel NH3: Basisvektoren a,b,c entlang NH-Bindungen
v"
Ha
Hb
N
Hc
a b (a')
b a (b')
c c (c')
Spiegelung an v"
Transformationsmatrix:
a ' 0 1 0 a  0  a  1  b  0  c b
b' = 1 0 0 b = 1  a  0  b  0  c = a 
  
  
  
 c'  0 0 1  c  0  a  0  b  1  c  c 
Basis N-H Bindungsvektoren von NH3 (C3v-Symmetrie)
3 x 3 Transformationsmatrizen für Symmetrieoperationen
1 0 0


E 0 1 0
0 0 1
v
1 0 0


0
0
1


0 1 0
0 0 1


C13 1 0 0
0 1 0
0 1 0


C 23 0 0 1
1 0 0
0 0 1 
0 1 0
' v 0 1 0 "v 1 0 0


0 0 1
1 0 0
Darstellung von C3v ?
 Multiplikationstafel
1 0 0 0 0 1 1  0  0  1  0  0 1  0  0  0  0  1 1  1  0  0  0  0
v C13 = 0 0 1  1 0 0 = 0  0  0  1  1  0 0  0  0  0  1  1 0  1  0  0  1  0

 
 

0 1 0 0 1 0 0  0  1  1  0  0 0  0  1  0  0  1 0  1  1  0  0  0
0 0 1 
= 0 1 0 = ' v
korrekt


1 0 0
Vergleich mit den Translationsvektoren: Tx, Ty, Tz
Transformationsmatrizen (3 x 3) Tx, Ty, Tz für NH3 (C3v)
1 0 0


E 0 1 0
0 0 1
C 23
' v
C13
  (1 / 2 )

  (  3 / 2)

0

  (1 / 2 )  (  3 / 2 ) 0



(

3
/
2
)

(
1
/
2
)
0



0
0
1

  (1 / 2 )

  (  3 / 2)

0

 (  3 / 2 ) 0

 (1 / 2 ) 0
0
1
v
 1 0 0


0

1
0


 0 0 1
 (  3 / 2 ) 0

 (1 / 2 ) 0 "v
0
1
  (1 / 2 )

 (  3 / 2)

0

0 0 1 
C13 1 0 0


0 1 0
zum Vergleich
Bindungsvektoren
 (  3 / 2 ) 0

 (1 / 2 ) 0
0
1
Unterschiede der Darstellungen/Matrizen
Darstellung:
Tx, Ty, Tz
  (1 / 2 )  (  3 / 2 ) 0

1 
C 3   (  3 / 2 )  (1 / 2 ) 0


0
0
1


von Null-verschiedene Elemente:
in Blöcken  "Blockmatrix":
hier: 2x2 und 1x1
Bindungsvektor
0 0 1 
C13 1 0 0


0 1 0
von Null-verschiedene
Elemente "zufällig" verteilt
In jeder beliebigen Darstellung sind die von Null-verschiedenen
Matrixelemente zufällig verteilt!
lassen sich aber in Blockmatrizen überführen (Ausreduzieren)
Y1
Aus-
"0"
Y2
Y3
X
reduzieren
"0"
Ym
X-Matrix
Y1, Y2 ... Ym Matrizen  Darstellungen der Punktgruppe
Beispiel NH3 (C3v-Symmetrie):
Tx, Ty 2 x 2 Blockmatrix/Darstellung
Tz
1x1
""
X-Matrix: reduzible Darstellung
Y-Matrizen: irreduzible Darstellungen
Bedeutung irreduzibler Darstellungen
Atom- oder Molekülorbital, Molekülschwingung ..:
 Basis für eine irreduzible Darstellung
Eigenschaften der Orbitale..
abhängig von ihrer irreduziblen Darstellung
Aus: reduziblen Darstellungen  irreduzible Darstellungen
Wie? später?
 zunächst wichtige Matrizeneigenschaften
Charakter (Spur) einer Matrix, c
 a 11

 a 21
 ...

 ...
 a n1

a 12
a 22
...
...
a n2
a 13
a 23
...
...
a n3
....... a 1n 

....... a 2 n 
....... ... 

....... ... 
....... a nn 
Summe der Diagonalelemente
c = a11 + a22 + a33 + ...... + ann = Saii (i = 1.. n)
c nur definiert für quadratische Matrix (Anzahl Spalten = Anzahl Zeilen)
Charakter gibt wichtige Eigenschaften einer Matrix wider!
"erspart viel Schreibarbeit"
Transformationsmatrizen für Bindungsvektoren in C3v-Symmetrie
1 0 0


E 0 1 0
0 0 1
0 1 0

2 
C 3 0 0 1
1 0 0
' v
0 0 1


0 1 0
1 0 0
c= 3
c= 0
c= 1
0 0 1

1 
C 3 1 0 0
0 1 0
v
"v
1 0 0


0 0 1
0 1 0
0 1 0


1
0
0


0 0 1
c= 0
c= 1
c= 1
Transformationsmatrizen für Tx,Ty,Tz-Vektoren
1 0 0


E 0 1 0
0 0 1
c= 3
  (1 / 2 )  (  3 / 2 ) 0


C 23   (  3 / 2 )  (1 / 2 ) 0

0
0
1

' v
  (1 / 2 )  (  3 / 2 ) 0


C13   (  3 / 2 )  (1 / 2 ) 0

0
0
1

  (1 / 2 )  (  3 / 2 ) 0



(

3
/
2
)

(
1
/
2
)
0



0
0
1

c= 0
c= 1
v
"v
1 0 0


0

1
0


0 0 1
c= 0
c= 1
  (1 / 2 )  (  3 / 2 ) 0



(

3
/
2
)

(
1
/
2
)
0



0
0
1

c= 1
Eigenschaften von Charakteren einer Tranformationsmatrix
1.
Symmetrieoperationen der gleichen Klasse haben den
gleichen Charakter:
für unser Beispiel in C3v-Symmetrie: C31 and C32 sowie v's
2.
Für unabhängige Vektoren wird der gleiche Charakter
erhalten:
für unser Beispiel in C3v-Symmetrie: Bindungs- u. Translationsvektoren
Die Summe der Charaktere der irreduziblen Komponenten ergibt
den Charakter der reduziblen Darstellung.
Symm-Ops der gleichen Klasse  gleicher Charakter:
Charakter der Klasse wird nur einmal aufgeführt:
E
2C3
3v
3
2
1
0
-1
1
1
0
1
reduzible Darstellung
irreduzible Darstellungen
(Bdgs.- oder Translationsvektor)
(2 x 2)
(1 x 1)
Bezeichnung/Symbole der irreduziblen Darstellungen
MULLIKEN-SYMBOLE
1 x 1 Darstellungen/Matrizen
2 x 2 Darstellungen/Matrizen
3 x 3 Darstellungen/Matrizen
A
B
A oder B
E
T
c > 0 bzgl. Drehung um Hauptachse
(symmetrisch bzgl. Drehung)
c < 0 bzgl. Drehung um Hauptachse
(antisymmetrisch bzgl. Drehung)
zusätzliche Indizes:
g
u
c > 0 bzgl. Inversion ('gerade')
c < 0 bzgl. Inversion ('ungerade')
(d.h. symmetrisch/antisymmetrisch bzgl. i)
'
"
c > 0 bzgl. Spiegelung an h (symm.)
c < 0 bzgl. Spiegelung an h (antisymm.)
1
zusätzliche Unterscheidungen bzgl.
Drehungen und Spiegelungen
2
3
CHARAKTERTAFELN
C2v
E
C2
xz
yz
A1
A2
B1
B2
+1
+1
+1
+1
+1
+1
-1
-1
+1
-1
+1
-1
+1
-1
-1
+1
Mulliken
Symbole
Tz
Rz
Tx oder Ry
Ty oder Rx
C3v
E
2C3
3v
A1
A2
E
+1
+1
+2
+1
+1
-1
+1
-1
0
Tz
Rz
(Tx, Ty) oder (Rx, Ry)
Charaktertafeln
- Aufstellung der Charaktere der Transformationsmatrizen
für alle irreduziblen Darstellungen einer Punktgruppe
- Tafeln für sämtliche Punktgruppen verfügbar
 werden demnächst verteilt
Wie erhält man aus einer reduziblen Darstellung
die irreduziblen Komponenten?
Ausreduzieren
Ausreduzier-Formel
1
a p =  c( R ) c p ( R )
h R
ap = Anzahl der irreduziblen Darstellung p in der reduziblen Darstellung
h = Anzahl der Symm-Op´s der Punktgruppe = Ordnung der Punktgruppe
c(R) = Charakter der Symm-Op R der reduziblen Darstellung
cp(R) = Charakter der Symm-Op R der irreduziblen Darstellung p
(z.B. a2)  aus Charaktertafel
 abstrakt! am besten erklärt durch Beispiele!
Beispiel Bindungsvektordarstellung: NH3 (C3V-Symmetrie)
reduzible Darstellung
E
3
2C3
0
3v
1
Schwingungsmoden aus irreduzibler Darstellung
benötigt wird Charaktertafel
C3v
E
2C3
3v
A1
A2
E
+1
+1
+2
+1
+1
-1
+1
-1
0
Ausreduzieren
1
a p =  c( R ) c p ( R )
h R
E
3
2C3
0
3v
1
a A1
1
= [( 3  1)  (0  2  1)  (1  3  1)] = 1
6
a A2
1
= [( 3  1)  (0  2  1)  (1  3  1)] = 0
6
1
a E = [( 3  2)  (0  2  1)  (1  3  0)] = 1
6
GBindungsvektor = A1 + E
G: Symbol für reduzible Darstellung
h=1+2+3=6
C3v
E
A1 +1
A2 +1
E +2
2C3 3v
+1
+1
-1
+1
-1
0
Schwingungsspektroskopie - Prinzip
H
r0
Cl
Hook´sches Federmodell
mechanische Feder
k
Auslenkung aus r0
Energieaufnahme E
r0 wird sich wieder einstellen
Schwingung
F=-k.x
E = - ½ . k . x2
harmonischer Oszillator - IR-Spektroskopie
Schwingung: Anregung durch elektromagnetische Wellen (hn)
V(r)
E4 = 9/2 hn
n=4
E3 = 7/2 hn
n=3
E2 = 7/2 hn
E1 = 5/2 hn
hn
n=2
hn
n=1
hn
n=0
E0 = 1/2 hn
rr00
Atomabstand r
V(r) = ½ k . x2 = 2 2 . m .nosc .x2
V(r): potentielle Energie k: Kraftkonstante
x: Auslenkung
m: reduzierte Masse
nosc: Schwingungsfrequenz des harm. Oszillators
1
n osc =
2
k
m
höhere Frequenz für höhere Kraftkonstante k!
k Maß für Bindungsstärke (BDE)??
BDE
Korrelation k mit Bindungsabstand r0
[kcal/mol]
Badger´s Regel
k = 1.86 (r0- dij)-3
dij = Konstante für Atome i und j von Periode i und j
k [mdyn/Å]
erfüllt!
harmonischer Oszillator
V(r)
E4 = 9/2 hn
n=4
E3 = 7/2 hn
n=3
E2 = 7/2 hn
E1 = 5/2 hn
hn
n=2
hn
n=1
hn
n=0
E0 = 1/2 hn
rr00
Atomabstand r
Auswahlregel: Dn = 1
aber! anharmonisches Potential = Bindungsbruch für r >> r0
!
anharmonisches Potential - Morsepotential
H
H
H
H
BDE
andere Auswahlregel!
Oberschwingungungen Dn = 2, 3 erlaubt!
intensitätsschwächer
Auswahlregeln - Normalkoordinatenanalyse
- Anzahl Molekül-Schwingungen (n) eines n-atomigen Moleküls ?:
- jedes Atom kann sich in x,y,z-Richtung bewegen: 3n-Freiheitsgrade
aber: nicht alle entsprechen Schwingungen:
z
Bewegung der Atome: Translation in y-Richtung
y
O
x
z
x
H
z
y
x
H
y
Massenschwerpunkt ändert sich!
keine Schwingung
analog Rotation Schwingung
zz
x O
y
z
x
H
z
y
x
H
H
O
H
y
Blick entlang z-Achse
lineare Moleküle:
3n-5 Schwingungen: z.B. CO2: 3x3-5=4 n´s
(-3 Translationen -2 Rotationen)
nicht-lineare Moleküle: 3n-6 Schwingungen: z.B. H2O: 3x3-6=3 n´s
(-3 Translationen -3 Rotationen)
Auswahlregeln
Resultat Quantenchemie
Dipolmoment muß sich bei Schwingung ändern!
Valenzschwingung
Bindungslängenänderung
IR-aktiv
O
O
O IR-aktiv
nasym: 2350 cm-1
H
H
C
nsym: 3652 cm-1
O
O
IR-aktiv
O
nasym: 1340 cm-1
H
H
C
IR-inaktiv
(Raman-aktiv)
nasym: 3756 cm-1
Deformationsschwingung
Winkeländerung
IR-aktiv H
O
O
H
-1
nsym: 1596 cm
C
O
666 cm-1 entartet
O
+
C
-
-1
O
+
666 cm entartet
IR-aktiv
Wie bestimmt man die "erlaubten" Schwingungen?
Vorhersage/Ermittlung mittels Gruppentheorie/Symmetrieeigenschaften
jede Schwingungsmode zeigt ein eigenes "Muster (Vektor)"
für die Verrückung der Atome(Dx,Dy,Dy)
Eigensymmetrie = irreduzible Darstellung
Bei Kenntnis des Aussehehens der Schwingungsmoden:
Bestimmung der irreduziblen Darstellung
Anwendung der Auswahlregeln.
Schwingungsmoden sind aber i.a. NICHT bekannt!!
Bestimmung der Moden durch Ausnutzung der Symmetrieeigenschaften
Lösungsansatz:
- 3 Vektoren (x,y,z) für jedes Atom des Moleküls 3n Vektoren
 3n Darstellungen: G3n
z3
x3 3
y3
z1
x1
1
9 Basisvektoren entlang Achsen
z2
y1
z.B. H2O
x2
2
y2
Anwendung der Symmetrieoperationen: C2v-Symmetrie (E, C2, v, v´)
z3
C2
x3 3
y3
z1
x1
1
z2
y1
x2
2
H2O:
C2-Achse:
x1  -x2
x2  -x1
x3  -x3
y1 -y2
y2  -y1
y3  -y3
z1  z2
z2  z1
z3  z3
y2
Transformation in Matrixschreibweise
C2
E
x1  x1 y1 y1
x2  x2 y2  y2
x3  x3 y3  y3
z1  z1
z2  z2
z3  z3
x1 y1 z1 x2 y2 z2 x3 y3 z3
1

0
0

0
0

0
0

0

0
0 0 0 0 0 0 0 0

1 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0

0 0 1 0 0 0 0 0
0 0 0 1 0 0 0 0

0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0

0 0 0 0 0 0 1 0

0 0 0 0 0 0 0 1
x1  -x2 y1  -y2 z1  z2
x2  -x1 y2  -y1 z2  z1
x3  -x3 y3  -y3 z3  z3
x1 y1 z1
0
0

0
0
0
0

 1 0
 0 1

0
0
0
0

0
0

0
0
x2 y2 z2 x3 y3 z3
0 1
0
0
1 0
0 1
0 0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0

0
0 0
0
0 0

0
0 0
0
0 0

0
0 0
 1 0 0

0  1 0

0
0 1
0
0
Transformationsmatrix: dreiatomiges Molekül in C2v Symmetrie
1
0

0

0
0

0
0

0
0
0
1
0
0
0
0
0
0
0
0 0

0 0
0 0

1 0
0  1

0 0
0 0

0 0

0 0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
0 1
0
0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 0
0 0
1 0
0 0
0
0
0
0 0
0 0
0 1
0 0
0 0
0
0
0 0
0 0
0
0
0
0
0
0
0
1
0
0
0

0

0
0

0
0

0
1
0

0 0
0 0

0 0
0 0

0 0
0 0

 1 0

0 1
E
c(E) = 9
0
xz
c(xz) = 1
0
0

0
0
0
0

 1 0
 0 1

0
0
0
0

0
0

0
0
 1

0
0

0
0

0
0

0

0
0 1
0
0

0
0 0
0
0 0

0
0 0
0
0 0

0
0 0
 1 0 0

0  1 0

0
0 1
0
0
1 0
0 1
0 0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0 0
0
0 0
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0
0 0
0 0
0
0
0
1 0
0 1
0 0
0 0
0 0
0
0
0 0
0 0
0
0 0

0 0 0
0 0 0

0 0 0
0 0 0

0 0 0
 1 0 0

0 1 0

0 0 1
C2
c(C2) = -1
0
yz
c(yz) = 3
E C2 xz yz
Charakter: 9 -1 1 3
Transformationsmatrix schwierig zu analysieren
speziell für größere Moleküle
wichtig nur Charakter c der Matrix
C2: c(C2) = -1
0
0

0
0
0
0

 1 0
 0 1

0
0
0
0

0
0

0
0
0 1
0
0
1 0
0 1
0 0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0

0
0 0
0
0 0

0
0 0
0
0 0

0
0 0
 1 0 0

0  1 0

0
0 1
0
C2
0
1
3
2
1 2
2 
3 3
bzgl. C2: nur Atom 3!
nur unbewegte Atome tragen zur Spur/Charakter bei!!!!!!
Beitrag unverschobener Atome bzgl. E: +3 pro Atom
E: c(E) = 9
1
0

0

0
0

0
0

0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
0

0

0
0

0
0

0
1
hier: 9/3 = 3
Auswirkung von Inversionszentren, i
z
ii
y
x
x'
y'
z'
0
 1 0
[x' y' z' = [x y z 0  1 0 
0  1
 0
Beitrag von -3 pro unverschobenem Atom zu c(i) in G3n
Auswirkung einer Spiegelebene, 
xzxz
z
y
z'
y'
2 Achsen in Ebene
x


x'
1 0 0
[x' y' z' = [x y z 0  1 01
0 0

1 

Beitrag von -3 pro unverschobenem Atom zu c() in G3n
Auswirkung einer Drehachse, Cn
z'
y
x'
(360/n)
z
x
(360/n)
y'
 cos a sin a 0
[x' y' z' = [x y z  sin a cos a 0 a = (360/n)°
 0
0
1
Beitrag eines unverschobenen Atoms zu c(Cn) in G3n: 1+2·cos(360/n)
z.B. C2-Achse: 1+2·cos(180)=1+2·(-1)=-1
Auswirkung einer Drehspiegelachse, Sn
 cos a sin a 0 
[x' y' z' = [x y z sin a cos a 0 
 0
0
 1
Drehung wie Cn-Achse: z´=-z
Beitrag eines unverschobenen Atoms zu c(Cn) in G3n: -1+2·cos(360/n)
z.B. S4-Achse: -1+2·cos(90)=-1+2·(0)=-1
Zusammenfassung:
Beiträge zu c(R)/pro unverschobenem Atom von G3N:
R = E
i

Cn
Sn
+3
-3
+1
+1+2·cos(360/n))
-1 +2·cos(360/n))
ergibt für unser 3-atomiges Molekül:
Anzahl unverschobener Atome
c(R)/pro unverschobenem Atom
G3N
E
3
3
9
(3·3)
C2
1
-1
-1
xz
1
1
1
yz
3
1
3
(1·-1)
(1·1)
(3·1)
Aussehen der irreduziblen Darstellungen?
Ausreduzieren liefert: a p =
G3N
A1
A1
1
c( R ) c p ( R )

h R
9
-1
1
3
+1
+1
+1
+1
aA1=1/4·(9·1+(-1)·1+1·1+3·1)=1/4·12 = 3 3 A1
G3N
B
B1
1
9
-1
1
3
+1
1
1
-1
aB2=1/4·(9·1+(-1)·1+1·1+3·(-1))=1/4·6 = 2 2 B1
C2v
E
C2
xz
A1
A2
B1
B2
+1
+1
+1
+1
+1
+1
-1
-1
+1
-1
+1
-1
yz
+1
-1
-1
+1
h=4
Tz
Rz
Tx, Ry
Ty, Rx
analog für A2 und B2
G3N = 3A1 + A2 + 2B1 + 3B2
G3N = 3A1 + A2 + 2B1 + 3B2
beinhaltet noch 3 Translationen und 3 Rotationen
GT = A1 + B1 + B2
GR = A2 + B1 + B2
Gvib= G3n -(GT +GR )
Gvib= 3A1 + A2 + 2B1 + 3B2 - A1 - B1- B2 - A2 - B1 - B2
= 2A1 + B2
C2v
E
C2
xz
A1
A2
B1
B2
+1
+1
+1
+1
+1
+1
-1
-1
+1
-1
+1
-1
yz
+ 1 Tz
-1
Rz
-1 Tx, Ry
+1 Ty, Rx
Weitere Beispiele zur Bestimmung von Gvib, via G3N:
NH3
N
(C3v)
H
H
H
C3v
E
unverschobene Atome
4
c/unverschobenes Atom 3
\ G3N
2C3
1
0
12
0
3v
2
1
2
Ausreduzieren G3N = 3A1 + A2 + 4E
GT+R (Charaktertafel) = A1 + A2 + 2E
Gvib = 2A1 + 2E
Jede E-Mode entspricht 2 Schwingungen (2-fach entartet)
H
CH4 (Td)
C
H
H
Td
unversch. Atome
c/u.A.
\ G3N
H
E
5
3
15
8C3
2
0
0
3C2
1
-1
-1
6S4
1
-1
-1
Ausreduzieren: G3N = A1 + E + T1 + 3T2
GT+R = T1 + T2,
Gvib = A1 + E + 2T2
E: 2-fach entartet; T: 3-fach entartet
6d
3
1
3
F
XeF4 (D4h)
F
Xe
D4h
u.A.
c/u.A.
E
5
3
2C4
1
1
\G3N
15
1
F
F
C2 2C2'
1 3
-1 -1
2C2" i 2S4
1
1 1
-1 -3 -1
-1
-3
-1
-1
-1
h 2v 2d
5
3
1
1
1
1
5
3
1
Ausreduzieren G3N = A1g + A2g + B1g + B2g +Eg +2A2u + B2u + 3Eu
GT+R (Charaktertafel) = A2g + Eg + A2u + Eu,
\
Gvib = A1g + B1g + B2g + A2u + B2u + 2Eu
Symmetrierasse der Schwingungsmoden läßt sich so bestimmen:
Art/Aussehen der Schwingung:
 INTERNEN KOORDINATEN Methode.
Verwendung interner Koordinaten
interne Koordinaten?
Änderung
Schwingungsmode
• Bindungslänge
Valenz- / Streckschwingung
• Bindungswinkel
Deformationsschwingung
• Torsionswinkel
""
Beispiel: C2v-symmetrisches Molekül
r1
H
O r2
q
H
Basisvektoren: Dr1, Dr2 (Streckschwing.)
Dq (Deformationsschwing.)
Charakter: nur unverschobene Vektoren berücksichtigt ( +1 to c).
C2v
GDef.
GStreck
E
1
2
C2
1
0
xz
1
2
yz
1
0
N.B. Transformationsmatrix für GStreck:
E, xz: 1 0
C2, yz :  0 1


0 1 
1
0




c=2
c=0
Bestimmung der irreduziblen Darstellungen
GDef. (1 1 1 1) : irreduzible Darstellung: A1
GStreck (2 0 2 0): keine irreduzible Darstellung
ausreduzieren
Ausreduzieren liefert: a p =
GStreck
A1
A1
1
c( R ) c p ( R )

h R
2
0
0
2
+1
+1
+1
+1
aA1=1/4·(2·1+0·1+0·1+2·1)=1/4·4 = 1
GStreck
B
B2
2
2
0
2
0
+1
-1
1
-1
aB2=1/4·(2·1+0·(-1)+2·1+0·(-1))=1/4·4 = 1
C2v
E
C2
xz
A1
A2
B1
B2
+1
+1
+1
+1
+1
+1
-1
-1
+1
-1
+1
-1
yz
+1
-1
-1
+1
h=4
Tz
Rz
Tx, Ry
Ty, Rx
A1
B1
GStreck= A1 + B1
Wasser: Schwingungsmoden
3n-6: 3.3-6= 3 Schwingungsmoden
2 Streckschwingungen: A1 + B1
1 Deformationsschwingung: A1
Symmetrierassen wichtig für Zuordnung
Charaktertafeln im Netz
http://www-theory.mpip-mainz.mpg.de/~gelessus/group.html
Charaktertafeln im Netz
reduziert aus....
IR & Raman-Aktivität
http://www-theory.mpip-mainz.mpg.de/~gelessus/group.html
Weiteres Beispiel - Ammoniak
rr11
N
r2 r3
H
H
rr23 H
q1 opposite
to r
q
1 gegenüber r11
to rr22
q22 opposite
gegenüber
q
gegenüber
q33 opposite
to rr33
Basis Valenzschwingung:
Dr1, Dr2, Dr3
Basis Deformationsschwingung: Dq1, Dq2, Dq3
C3v
GValenz
GDeform.
E
3
3
2C3
0
0
3
1
1
Ausreduzieren  GValenz = A1 + E
GDeform. = A1 + E
(bereits früher Gvib = 2A1 + 2E)
Bestimmung von Gvib via G3N
N
H
H
H
C3v
E
unverschobene Atome
4
c/unverschobenes Atom 3
\ G3N
2C3
1
0
12
0
Ausreduzieren G3N = 3A1 + A2 + 4E
GT+R (Charaktertafel) = A1 + A2 + 2E
Gvib = 2A1 + 2E
3v
2
1
2
H
Methan, CH4
r1
9 Schwingungsmoden
6 Winkel q1,.....q6,
r4 C r2
H
r
3
H
H
q1 liegt zwischen r1 und r2 etc.
Basen für Valenzschwingungen: Dr1, Dr2, Dr3, Dr4
Basen für Deformationsschwingungen: Dq1, Dq2, Dq3, Dq4, Dq5, Dq6
Td
GValenz
GDeform.
E
4
6
8C3
1
0
3C2
6S4
0
0
2
0
2
Ausreduzieren GValenz = A1 + T2
GDeform, = A1 + E + T2
6d
2
2
4 Moden
6 Moden
0Moden eine zuviel ! vgl.: Gvib = A1 + E + 2T2
eine A1 Mode zuviel!
Problem mit Winkelbasis q1 - q6:
• eine der Koordinaten ist redundant.
• nicht alle 6 sind linear unabhängig
• die 6. te Koordinate ergibt sich aus den restlichen 5 Winkeln
A1-Deformationsschwingung würde bedeuten:
gleichzeitige Vergrößerung aller 6 Winkel!
physikalisch/geometrisch unmöglich
Regel/Tip: zuerst Gvib berechnen.
GDef = A1 + E + T2
PtCl42-
r1
Cl r4
Cl
Pt
Cl r3
D4h
E
GValenz 4
2C4
0
Basis: Dr1,Dr2, Dr3, Dr4.
r2 Cl
C2
0
2C2' 2C2" i 2S4
2
0
0
0
h 2v 2d
4
2
0
Ausreduzieren GValenz = A1g + B1g + Eu
2 Typen von Derformationsmoden:
in der Ebene:
aus der Ebene heraus:
q4
Cl
Cl Definition schwierig (vertagt auf später)
q3 Pt q1
q2
Cl
Cl
D4h
E
GDef(Ebene) 4
2C4
0
C2
0
2C2' 2C2" i 2S4
0
2
0 0
h 2v 2d
4
0
2
Ausreduzieren GDef(Ebene) = A1g + B2g + Eu
Ergebnis: Gvib = A1g + B1g + B2g + A2u + B2u + 2Eu
GValenz
= A1g + B1g + Eu
GDef(Ebene) = A1g + B2g + Eu
wieder eine A1g-Mode zuviel:
"out-of-plane" Deformationsmoden: Differenzbildung
Go.o.p.Def = Gvib - GValenz - GDef(Ebene) = A2u + B2u
bis jetzt erreicht: Anzahl & Symmetrierasse
als nächstes Auswahlregeln für IR/Raman
Spektroskopische Auswahlregeln
allgemeingültig: gelten z.B. auch für UV/VIS-Spektroskopie
Spektroskopie:
End-/ anregter Zustand
Anregung
Übergang
Grund-/Ausgangszustand
Auswahlregeln
• nicht alle Übergange sind erlaubt
• einige Übergänge sind verboten
Ob Übergange erlaubt oder verboten ist, hängt von den
Symmetrieeigenschaften,
d.h. irreduziblen Darstellungen der Grund und Anregungszustände ab:
Intensität des Übergangs I hängt vom Übergangsmoment ab:
I
Es gilt:
( YEPYAdt )2
P = OPERATOR - hängt von der Art der Spektroskopie ab (z.B.Dipolmoment)
YE = Wellenfunktion des Endzustandes
YA = Wellenfunktion des Ausgangzustandes
Operator P : hängt von der Art der Spektroskopie ab.
für IR und elektronische Übergänge (UV/VIS):
WW des Moleküls und der Strahlung via Dipolmoment
Operator = Dipolmoment
"Ideale Welt": Exakte Berechnung des Übergangsdipolmoments
nicht möglich
"Reale Welt": Bestimmung: I = 0 = verboten
I  0 = erlaubt
Ohne Herleitung:

P

d
t
E
A

ist = 0 (verboten) außer wenn das Produkt
EPA
die totalsymmetrische irreduzible Darstellung enthält.
(Nur Übergänge für die iPf totalsymmetisch sind, sind erlaubt)
Totalsymmetrische irreduzible Darstellung einer Punktgruppe
alle c's = +1
Was heißt das nun praktisch - wie macht man´s?
"Ganz einfach": Bestimmung der Symmetrie des Produkts
zweier Wellenfunktion und eines Operators P
Berechnung der DIREKTPRODUKTE (dazu gleich mehr)
IR-Spektroskopie: Operator P = Dipolmoment m
Symmetrie von m?
z
m
mz
mx
x
my
y
Zur Erinnerung: m =Vektor
Vektorzerlegung in x, y und z-Komponente
mmx + my + mz
x,y,z-Komponenten des Dipolmoments haben gleiche Symmetrie
wie Translationsvektoren Tx, Ty, Tz!
in Charaktertafel tabelliert s. unter Tx, Ty, Tz
C2v
E
C2
xz
A1
A2
B1
B2
+1
+1
+1
+1
+1
+1
-1
-1
+1
-1
+1
-1
yz
+1
-1
-1
+1
Tz
mz
Rz
Tx, Ry mx
Ty, Rx my
Symmetrie der Wellenfunktionen YA und YE?
IR: YA und YE sind Wellenfunktionen der Schwingungen
Symmetrie & Aussehen der Wellenfunktionen?
YA einfach! - alle Schwingungsgrundzustände sind totalsymmetrisch,
gehören zur totalsymmetrischen Darstellung (A1..)
YE - Symmetrie der Wellenfunktion entspricht der Symmetrie
der entsprechenden angeregten Schwingungsmode!
z.B: Schwingungsmode mit B2-Symmetrie besitzt entsprechende
Wellenfunktion mit B2-Symmetrie.
Beispiel!
Streckschwingungsbanden mit A1 and E Symmetrie von Ammoniak
IR-aktiv?
A1 Mode: YA A1;
E
A1
C3v
m (Charaktertafel) A1 + E
A1
A2
E
E
+1
+1
+2
2C3
+1
+1
-1
3v
+1
-1
0
Tz, z
Tx, Ty x, y
Direktprodukt : A1 x (A1 + E) x A1
für A1 (mz)
A1
A1
A1
+1
+1
+1
1·1·1
A1
+1
=
A1
+1
+1 YA
+1
+1
mz
+1
+1 YE
1·1·1 1·1·1
+1
+1
= IR-aktiv totalsymmetrisch!
E Mode: YA A1;
m
YE
C3v
E
A1 + E
A1
A2
E
Direktprodukt : A1 x (A1 + E) x E
für E1 (mx,y)
A1
E
E
+1
+2
+2
1·2·2
+4
E
+1
+1
+2
2C3
+1
+1
-1
3v
+1
-1
0
Tz, z
Tx, Ty x, y
+1
+1 YA
-1
0
mz
-1
0
YE
1·-1·-1 1·0·0
+1
Ausreduzieren
E
2C3
+4
+1
+1
A1 +1
1/6·(1·4·1 + 2·1·1 +
+0
1
3v
a p =  c( R ) c p ( R )
h R
0
h=6
+1
3·0·1)= 1/6 (4+2) = 1
enthält 1x A1: totalsymmetrisch! = IR-aktiv!
Operator für Raman-Spektroskopie
IR:  Dipoloperator – Raman ?
Ramaneffekt: physikalische Grundlage
• Wechselwirkung von Molekülen mit sichtbarem Licht
• sichtbares Licht = oszillierendes elektro-magnetisches Feld
• leichte Elektronen können Oszillation des E-Feldes folgen,
• sehr viel schwerere Kerne hingegen nicht.
 Verschiebung negativer Ladung - positive Ladung bleibt liegen
INDUZIERTES DIPOLMOMENT
Induziertes Dipolmoment  Raman-Schwingungsübergänge
IR: permanentes Dipolmoment
Größe des induzierten Dipolmoments abhängig davon wie leicht
sich die e--Wolke verzerren läßt

Polarisierbarkeit: Symbol a.
Polarisierbarkeit = TENSOR = 3 x 3 Matrix
vgl. Dipolmoment (3 x 1) Vektor
Polarsierbarkeitstensor
a xx a xy

a = a yx a yy
a zx a zy
9 Komponenten
a xz 

a yz 
a zz 
Beachte: axy = ayx = symmetrische Matrix
Symmetrieeigenschaften der Komponenten?
axx gleiche Symmetrie wie x2; axy wie xy ..
Binärkombinationen ebenfalls in Charaktertafel tabelliert
Bestimmung Raman-aktiver Banden
 analog zu IR-Banden
Verwendung der Symmetrieeigenschaften der Komponenten des
Polarisierbarkeitstensors (anstelle des Dipolmoments)
Auswahlregeln - Kurzfassung
(a) Jede Mode mit gleicher Symmetrieeigenschaft wie Tx, Ty or Tz
ist IR-aktiv.
(b) Jede Mode mit gleicher Symmetrieeigenschaft wie x2, y2, z2, xy
etc. ist Raman-aktiv.
Bestimmung der Moden:
r1
H
O r2
q
H
Wasser: 3 Moden
GValenz= A1 + B1
(IR: beide erlaubt)
GDef.= A1
(IR: erlaubt)
GDef., GValenz - "Aussehen der Moden ?"
Projektionsoperator
Projektionsoperator
C2
r1
O r2
H
xz
H
yz
C2v
E
C2
xz
yz
r1 
r1
r2
r1
r2
A1
1·r1
1 ·r2
1 ·r1
A2
1 ·r1
1 ·r2
-1 ·r1
B1
1 ·r1
-1·r2
1 ·r1
Summe
1 ·r2 = 2r1 + 2r2

-1 ·r2 = r1 + r2- r1- r2
=0
-1 ·r2 = 2r1 - 2r2
GValenz= A1 + B1!
Projektionsoperator
Resultat: A1-Mode 2r1 + 2r2
B1-Mode 2r1 - 2r2
"heißt übersetzt" auf unser Koordinatensystem
r1
H
r1
O r2
H
A1-Mode
symmetrisch
H
O
O r2
H
B1-Mode
antisymmetrisch
H
H
analog
A1-Mode
"scissors"
Projektionsoperator - Ammoniak

2
3 C3
r3
r2
r3
r1
r1 
r1
r2
r1
r3
r2
r1
r3
r2
Projektionsoperator - Ammoniak
C3v
E
C3
A1
A2
E
+1 r1 +1 r3
+1 r1 +1r3
+2 r1 -1 r3
C32
1
2
3
+1 r2 +1 r1 +1 r3 +1 r2
+1 r2 -1 r1 -1 r3 -1 r2
-1 r2 0 r1 0 r3 0 r2
2r1+2r2+2r3
0
2r1-r2-r3
E: nur eine Mode! zweite durch Verwendung einer anderen Basis
z.B. r2-r3 (steht senkrecht auf r2 und r3)
C3v
E
E
C3
C32
1
+2 (r2-r3) -1 (r2-r1) -1(r1-r3) 0 (...)
2
0 (...)
3
0 (...) = 3r2-3r3
Projektionsoperator - Ammoniak
q2
N
H
q3
q1
H
GDeform. = A1 + E
H
1. E
2. E
Projektionsoperator - Ammoniak
GValenz =
A1
r3
+
r2
N
H
H
GDeform. = A1
2 r1 - r2 - r3
E
H
H
q3
H
2 q1 + 2 q2 + 2 q 3
Regenschirm!
H
3 r2 - 3 r3
+
N
H
H
H
r1
H
H
r2
N
r3
H
r1
H
2 r1 + 2 r 2 + 2 r3
r2
N
r3
H
r1
E
H
q3
q2
N
q1
H
2 q1 - q2 - q3
H
q2
N
q1
3 q2 - 3 q3
H
Auswahlregeln UV/VIS-Spektroskopie
H
H
Ethen: -*Übergang erlaubt?
H
H
* LUMO
hn
 HOMO
zunächst Punktgruppe bestimmen
Symmetrieoperationen
C2(x)
xz
yz
xy
3 Spiegelebenen
C2(z)
i
i, 3 C2-Achsen
C2(y)
H
H
H
ja
Dh
Molekül
F
l
u
H
ja linear? nein
ß
d
i?
ja 2 oder mehr nein
i
Cn, n > 2 ?
a
nein
g
ja
r
i?
Flußdiagramm 2 a
ja
m
C5 ? nein
m
1
Cv
Ih
Oh
Td
lineare Gruppen
z.B
C60
kubische Gruppen
H
H
von Flußdiagramm 1
Cn? N
H
J
H
J  ?N
h
J ? N
J n C2´s ^Cn ?
n2
N
 ?J
D2h
J i?N
h
N
n d ?
J
N
n v ?
N
J
S2n ?
N
Dnh
Dnd
Dn
Cn
S2n
Cnv Cnh
Cs
Ci
C1
F
l
u
ß
d
i
a
g
r
a
m
m
2
H
H
von Flußdiagramm 1
Cn? N
H
J
H
J  ?N
h
J ? N
J n C2´s ^Cn ?
n2
N
 ?J
D2h
J i?N
h
N
n d ?
J
N
n v ?
N
J
S2n ?
N
D2h
Dnd
Dn
Cn
S2n
Cnv Cnh
Cs
Ci
C1
F
l
u
ß
d
i
a
g
r
a
m
m
2
Symmetrierassen
*
i
1
g
B2g
C2(z) C2(y)
-1
-1
B3u
C2(x)

i
-1
C2(z) C2(y)
-1
-1
xz
C2(z)
u
i
C2(y)
xy

Bande erlaubt?
*

B2g
B3u
1
1
-1
-1
B2g.B3u
1·1
1
1
-1
-1
1
1
-1
-1·-1
1·-1
-1·1
1·-1
1
-1
-1
-1
B1u
-1
1
-1·1
-1
1
1
-1
-1
1·1 -1·-1
1
1
I ~ (   *m  dt )
2
B2gmB3u
B1uB1u = Ag!
mz
!
I  0 ! erlaubt
3