Kristallographie(2)_neu

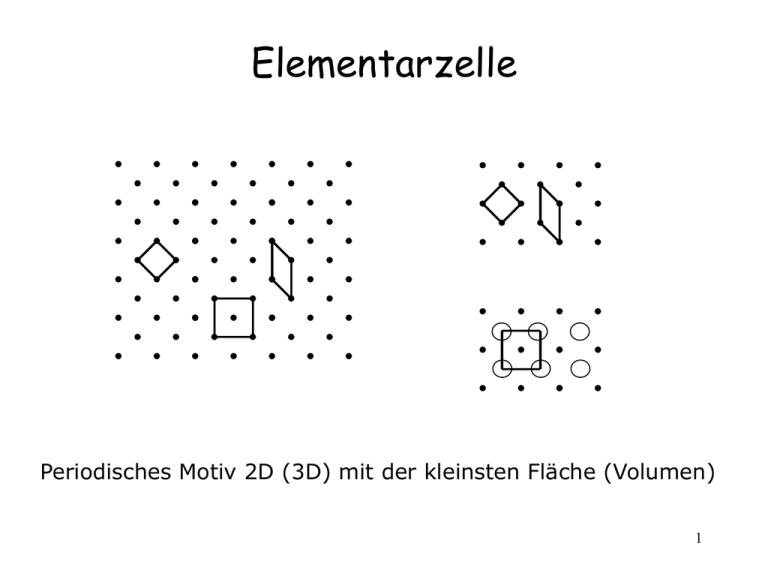
Elementarzelle
Periodisches Motiv 2D (3D) mit der kleinsten Fläche (Volumen)
1
Gitterparameter
C
B
c
a
A
b
Kantenlängen a, b, c
b
Winkel a, b, g
g
a
2
Kristallsysteme
Triklin: a≠b≠c, a≠b≠g
Monoklin: a≠b≠c, a=g=90°≠ b
(Ortho)rhombisch: a≠b≠c, a=b=g=90°
Tetragonal: a=b≠c, a=b=g=90°
Hexagonal: a=b≠c, a=b=90°, g=120°
Rhomboedrisch (trigonal): a=b=c, a=b=g≠90°
Kubisch: a=b=c, a=b=g=90°
7 (6) Kristallsysteme
rhomboedrische Elementarzelle kann man auch
in hexagonalen Achsen beschreiben
3
Anzahl der Atome (Moleküle) in einer
Elementarzelle
N
M
V

m au  Z i
i
1/8
1/4
1/2
1
N … Anzahl der Atome (Moleküle) in der
Elementarzelle
M … Masse aller Atome in der
Elementarzelle
m … Masse eines Moleküls
 … Dichte des Materials
V … Volumen der Elementarzelle
au … atomare Masseneinheit (1,66.10-27 kg)
Zi … Atommasse in AME (au)
4
5
Anzahl der Atome in einer
Elementarzelle – Beispiele
N
M
V

m au  Z i
i
Diamant (C)
Graphit (C)
Fulleren (C60)
Kubisch
a = 3,57 Å
 = 3,51 g/cm³
Hexagonal
a = 2,46 Å
c = 6,70 Å
 = 2,25 g/cm³
Kubisch
a = 14,17 Å
 = 1,68 g/cm³
V = a³
V = 45,5.10-24 cm³
Zi = 12
N=8
V = a²c sin120°
V = 35,1.10-24 cm³
Zi = 12
N=4
V = a³
V = 2845,2.10-24 cm³
Zi = 12
N = 240
Zi = 720
N=4
6
Kristallformen von Kohlenstoff
Fulleren
Diamant
o
a
b
o
c
a
c
Graphit
b
7
Anzahl der Moleküle in einer
Elementarzelle
N
M
V

m au  Z i
i
b
Steinsalz (NaCl)
Kubisch
a = 5,62 Å
 = 2,15 g/cm³
V = a³
V = 177,5.10-24 cm³
Zi = 23,0+35,5 = 58,5
N=4
c
o
a
8
Grundsymmetrieoperationen
Drehachse
nt
a
a
t
mt
mt  2t cos a  nt
nm
cos a 
  1,1
2
t
cos a
-1
-0.5
0
0.5
1
a
180
120
90
60
360
axis
2
3
4
6
1
9
Das Penrose Parkett
Eine ausgesprochen
unerwartete Entdeckung
begeisterte 1984 alle
Festkörperphysiker und
Kristallographen: Proben einer
sehr schnell abgekühlten
Aluminium-Mangan Legierung
(Al_6 Mn) kristallisierten als
kleine Ikosaeder und - noch
schlimmer - zeigten ein
Röntgenbeugungsbild mit
fünfzähliger Symmetrie und
ausgeprägten Maxima. Das
bedeutete, dass die Atome in
dieser Legierung irgendwie mit
fünfzähliger (Rotations-)
Symmetrie angeordnet sein
mussten.
A: 36° und 144°
B: 72° und 108°
Die genaue Anordnung der
Atome ist auch heute noch
nicht bekannt, aber es gibt ein
sehr gutes Modell. In zwei
Dimensionen ist das Modell
verblüffend einfach und auch
ästhetisch sehr ansprechend das Penrose Parkett.
10
Das Penrose Parkett – eine andere
Variante
11
Grundsymmetrieoperationen
Inversionszentrum
Spiegelebene
Verschiebung
12
Transformationen in der Kristallographie
x   M 11 x  M 12 y  M 13 z
y   M 21 x  M 22 y  M 23 z
z   M 31 x  M 32 y  M 33 z
x
x
y  M  y
z
z
13
Identität (1)
y
Drehachse „1“
[x,y,z]
x
x  x
1 0 0
y  y
z  z
M  0 1 0  E
0 0 1
14
_
Inversionszentrum (1)
y
[x,y,z]
x  x
y   y
z  z
x
[x’,y’,z’]
1
M
2
 0
0
0
0
1
1 0  0
0 1 0
0
0
1 0 0
M  0 1 0
0 0 1
1 0 0
1 0  0 1 0  E
0 1 0 0 1
15
Spiegelebene (m)
y
x1   x
[x1’,y1’,z1’]
y1  y
[x,y,z]
z1  z
1 0 0
M  0 1 0
0 0 1
x
[x2’,y2’,z2’]
x2  x
y2   y
z2  z
M
2
 E
x3  x
y3  y
z3   z
1 0 0
M  0 1 0
0 0 1
1 0
0
M  0 1 0
0 0 1
16
Drehachse
y
x  r cos a 1
[x’,y’,z’]
y  r sin a 1
x   r cos a  a 1 
a
y   r sin a  a 1 
[x,y,z]
a1
x   r cosa  a 1   r  cos a cos a 1  sin a sin a 1 
x
y   r sina  a 1   r  sin a cos a 1  cos a sin a 1 
x   x cos a  y sin a
y   x sin a  y cos a
cos a  sin a 0
M  sin a cos a 0
0
0
1
M
n
 E ; n
2
a
17
Drehachse
cos a
 sin a
0
M  sin a
0
cos a
0
0
1
Zähligkeit der Achse
Für die Drehachse
entlang c
a=360°/n
2
180°
3
120°
4
90°
6
60°
 1 0 0


M2   0 1 0
 0 0 1


 1
 2
M 3   23

 0


3
2
1
2

0
0 
0

1

 0 1 0 


M4   1 0 0
0 0 1


 1
 2
M 6   23

 0


3
2
1
2
0
0 
0

1

18
Kopplung der
Symmetrieoperationen
Drehachsen
1, 2, 3, 4, 6
+ Spiegelebene
senkrecht zu den
Drehachsen
+ Inversion
(Drehinversionsachsen)
-1, -2, -3, -4, -6
19
Kopplung der
Symmetrieoperationen
-1, -3 und -4 sind die
einmaligen
Symmetrieoperationen
-2 und -6 sind es nicht, weil:
-2 = m
-6 = 3/m
20
Kombination der
Symmetrieoperationen
Drehachsen mit senkrechter Spiegelebene
21
Kombination / Kopplung der
Symmetrieoperationen
Oktaeder
Tetraeder
22
Kombinationen der
Symmetrieoperationen
Drehachsen mit parallelen Spiegelebene(n)
23
Kombinationen der
Symmetrieoperationen
Kombination von Drehachsen
24
Kombinationen der
Symmetrieoperationen
Kombination von Drehachsen und Spiegelebenen
25
Kombinationen der
Symmetrieoperationen
Kombination der Drehspiegelachsen mit Drehachsen und
Spiegelebenen
26
Drehinversionsachsen
_ _ _ _ _
( 1, 2, 3, 4, 6)
|1 0 0|
1 = |0 1 0|
|0 0 1|
_
|-1 0 0|
1 = | 0 -1 0|
| 0 0 -1|
_
|-1 0 0|
1.1 = | 0 -1 0|
| 0 0 -1|
|-1 0 0|
2 = | 0 -1 0|
| 0 0 1|
_
|1
2.1 = |0
|0
|-1/2 -3/2 0|
3 = |3/2 -1/2 0|
| 0
0 1|
_
| 1/2
3.1 = |-3/2
|
0
|0 -1 0|
4 = |1 0 0|
|0 0 1|
_
| 0
4.1 = |-1
| 0
| 1/2 -3/2 0|
6 = |3/2
1/2 0|
| 0
0 1|
0 0|
1 0| = m(x,y)
0 -1|
3/2 0|
1/2 0|
0
-1|
1 0|
0 0|
0 -1|
_
| -1/2 3/2
6.1 = | -3/2 -1/2
|
0
0
0|
0|
-1|
27
Kombinationen der
Symmetrieoperationen
Ergeben 32 Kristallklassen (Punktgruppen)
System
Triklin
Monoklin
Rhombisch
Tetragonal
C1, Ci
Cs, C2, C2h
C2v, V, Vh
C4, C4h, C4v, D4, D4h, S4, Vd
Hexagonal
Trigonal
C6, C6h, C6v, D6, D6h
C3, C3i, C3v, D3, D3d, C3h, D3h
Kubisch
T, Th, Td, O, Oh
1, 1
2
m
222, 2mm, mmm
4
4 2 2
4, 4, , 422, 4mm, 4 2m,
m
mmm
2
3, 3, 32, 3m, 3 , 6, 6, 622, 6mm,
m
6 6 2 2
6 m2, ,
m mmm
2
4 2
23, 432, 3, 4 3m, 3
m
m m
2, m,
28
Die Mindestsymmetrie in
Kristallsystemen
System
Triklin
Monoklin
Rhombisch
Tetragonal
Hexagonal
Trigonal
Kubisch
1 oder 1 
1 2 oder 2 
3  2 oder 2 
1 4 oder 4 
1 6 oder 6 
1 3 oder 3 
4  3 oder 3 
1, 1
2
m
222, 2mm, mmm
4
4 2 2
4, 4, , 422, 4mm, 4 2m,
m
mmm
2
6 6 2 2
3, 3, 32, 3m, 3 , 6, 6, 622, 6mm, 6 m 2, ,
m
m mmm
2
4 2
23, 432, 3, 4 3m, 3
m
m m
2, m,
29
Symmetrieelemente in einem
Würfel
3 4
43
6 2
9 m
1 1
30
Die 32 Punktgruppen
31
Die 32 Punktgruppen
32
Gittertranslation

Zentrierte (Bravais) Gitter:
–
–
–
–
–

P [primitiv]: (x,y,z)
I [innenzentriert (raumzentriert)]: (x,y,z) + (1/2,1/2,1/2)
F [flächenzentriert]: (x,y,z) + (1/2,1/2,0), (1/2,0,1/2), (0,1/2,1/2)
C [zentrierte C Fläche]: (x,y,z) + (1/2,1/2,0)
R [rhomboedrisch]: (x,y,z) + (1/3,1/3,1/3), (2/3,2/3,2/3)
Gleitspiegelebenen
– Spiegelung + Verschiebung entlang der a, b oder c Achse (a/2, …)
– Spiegelung + Verschiebung entlang der Diagonale (n = a/2+b/2, …)
– Spiegelung + Verschiebung entlang der Diagonale
[Diamantverschiebung] (d = a/4+b/4, …)

Schraubenachsen :
– 21, 31, 32, 41, 42, 43, 61, 62, 63, 64, 65 – Drehachse + Verschiebung
entlang der Schraubenachse
33
Gittertranslation
Erweiterte Notation für die
Matrix der
Symmetrieoperationen
Gitter(sub)translation
x   M11 x  M12 y  M13 z  t ( x )
y   M 21 x  M 22 y  M 23 z  t ( y )
z   M 31 x  M 32 y  M 33 z  t ( z )
x
M11
M12
M13
t ( x)
x
t ( x)
y
M 22
M 23
t ( y)
y
y   M  y  t ( y)
M 21
z
M 32
M 33
t ( z)
z
M 31
1
0
0
0
1
x
x
z
t ( z)


z
1
34
Bravais Gitter (Translationsgitter)
Triklin: P
Monoklin: P, I
Orthorhombisch:
P, I, F, C
35
Bravais Gitter (Translationsgitter)
Tetragonal: P, I
Hexagonal: P, R
Kubisch: P, I, F
36
Kubisches Gitter
Gefülltes Volumen: x = V (Atome) / V (Elementarzelle)
Primitiv
Raumzentriert
Flächenzentriert
b
b
b
o
a
o
a
o
a
c
c
c
a
a  2r
VEZ  8r
3
V Atome  43 r 3
x
V Atome 
  52%
VEZ
6
4r
3
3
 4r 
VEZ  
  12,3  r 3
 3
VAtome  2  43 r 3
x
VAtome  3

 68%
VEZ
8
a
4r
2
3
 4r 
VEZ  
  22,6  r 3
 2
V Atome  4  43 r 3
x
VAtome  2

 74%
VEZ
6
37
Gleitspiegelebenen
c
b
a
Verschiebung entlang b
T = b/2
Gleitspiegelebene
(Verschiebung entlang b) +
Spiegelebene
38
Gleitspiegelebenen
Mögliche Gleitspiegelebenen
Typ der Verschiebung
entlang der a Achse
entlang der b Achse
entlang der c Achse
entlang der Diagonale
Diamantverschiebung
Symbol
a
b
c
n
d
Translationsvektor
a/2
b/2
c/2
a/2+b/2, b/2+c/2, c/2+a/2
a/4+b/4,b/4+c/4,c/4+a/4
39
Schraubenachse
Kombination der Drehachse und der Gittertranslation
entlang der jeweiligen Achse
Bezeichnung: MN; M ist das Symbol für die
Drehachse, N ist die Verschiebung in den 1/MEinheiten des Gitterparameters
mt
T
n
c/2
c
c/2
40
Schraubenachsen
2, 21
3, 31, 32
4, 41, 42, 43
6, 61, 62, 63, 64, 65
41
Symbole der Symmetrieelemente
42
Kombination der
Symmetrieoperationen
Kombination von
Drehachsen + Inversion + Spiegelebenen
ergibt
32 Punktgruppen (Kristallklassen)
Kombination von
Drehachsen + Inversion + Spiegelebenen + Zentrierung +
Gleitspiegelebenen + Schraubenachsen
ergibt
230 Raumgruppen
Zu finden in: International Tables for X-ray Crystallography, Vol. A
43