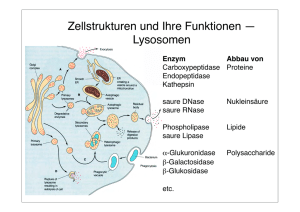
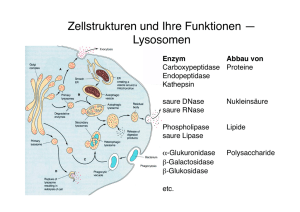
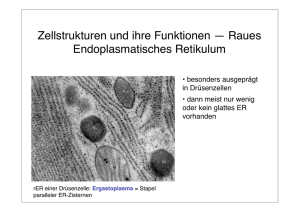
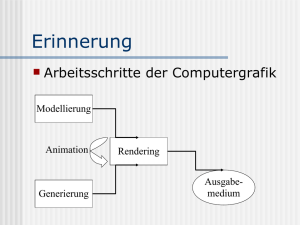
Modellierung von Zellstrukturen

Modellierung von Zellstrukturen
Dynamisches Verhalten
Mathematische Ansätze
Rechenverfahren
Modellierung von Zellstrukturen
1
Modellierung von Zellstrukturen
Stoffunabhängige Gleichungen
Materialgesetze
Kompatibilität
15 Unbekannte:
x y z xy xz yz
x y z xy xz yz
uvw
Modellierung von Zellstrukturen
2
Mathematische Ansätze
3 stoffunabhängige Gleichgewichtsgleichungen
6 kinematische Gleichgewichtsgleichungen
6 Materialgleichungen
Modellierung von Zellstrukturen
3
Stoffunabhängige Gleichungen
Gleichgewichtsgleichungen
F
a
F
b
Virtueller Schnitt
Modellierung von Zellstrukturen
4
Stoffunabhängige Gleichungen
Gleichgewichtsgleichungen
F
Normalspannungen
=dFn/dA
dFn
dA
dF
dFt
Spannungsvektor der
resultierenden Schnittgrößen
Sv=dF/dA
Tangentialspannungen
=dFt/dA
Modellierung von Zellstrukturen
5
Stoffunabhängige Gleichungen
z
zx
Gleichgewichtsgleichungen
zy
yz
xz
xy yx
y
x
Modellierung von Zellstrukturen
6
Stoffunabhängige Gleichungen
Gleichgewichtsgleichungen:
x/x + yx/y + zx/z + X = 0
y/y + xy/x + zy/z + Y = 0
z/z + yz/y + xz/x + Z = 0
Modellierung von Zellstrukturen
7
Modellierung von Zellstrukturen
Eliminiert man aus den 15 Gleichungen alle Spannungen so resultieren
3 partielle Differentialgleichungen für die unbekannten Verschiebungen:
G [u + (1-2) –1 (/x)] +X = 0
G [v + (1-2) –1 (/y)] +Y = 0
(Navier)
G [w + (1-2) –1 (/z)] +Z = 0
Modellierung von Zellstrukturen
8
Modellierung von Zellstrukturen
In den Navier Gleichungen sind:
u = 2u/x2+ 2u/y2 + 2u/z2
v = 2v/x2+ 2v/y2 + 2v/z2
w = 2w/x2+ 2w/y2 + 2w/z2
Modellierung von Zellstrukturen
(Laplace)
9
Modellierung von Zellstrukturen
Eliminiert man aus den 15 Gleichungen die Verschiebungen und deren
Ableitungen so resultieren 3 partielle Differentialgleichungen für die
unbekannten Spannungen:
 x+(1+)–1(2/x2)+2X/x+(1-)–1(X/x +Y/y +Z/z) = 0
 y+(1+)–1(2/y2)+2Y/y+(1-)–1(X/x +Y/y +Z/z) = 0
 z+(1+)–1(2/z2)+2Z/z+(1-)–1(X/x +Y/y +Z/z) = 0
(Beltrami)
Modellierung von Zellstrukturen
10
Modellierung von Zellstrukturen
 xy+(1+)–1 (2/xy) + X/y + Y/x = 0
 xz+(1+)–1 (2/xz) + X/z + Z/x = 0
 yz+(1+)–1 (2/yz) + Y/z + Z/y = 0
(Beltrami)
Modellierung von Zellstrukturen
11
Modellierung von Zellstrukturen
In den Beltrami-Gleichungen sind:
 x= 2x/x2+ 2x/y2 + 2x/z2
 y= 2y/x2+2y/y2 + 2y/z2
 z = 2z/x2+ 2z/y2 +2z/z2
Die Lösung der DGL (Navier + Beltrami) gelingt nur in seltenen Fällen
bei einfacher Geometrie und einfacher Belastung
Modellierung von Zellstrukturen
12
Stoffunabhängige Gleichungen
S - ü = 0
Spannungstensor
Bechleunigungsvektor
Modellierung von Zellstrukturen
13
Stoffunabhängige Gleichungen
Gleichgewichtsgleichungen:
Sx= xex + yxey+ xzez
Sy= yxex + yey + yzez
S=
Sz= zxex + zyez + zez
Tensordarstellung:
x
xy
xz
yx
y
yz
zx
zy
z
S Spannungstensor
Modellierung von Zellstrukturen
14
Modellierung von Zellstrukturen
15 Unbekannte:
x y z xy xz yz
x y z xy xz yz
uvw
3 Stoffunabhängige Gleichungen
6 Materialgleichungen
6 Kompatibilitätsgleichungen
Modellierung von Zellstrukturen
15
Modellierung von Zellstrukturen
Kompatibilitätsbedingung:
Benachbarte materielle Teile
werden nach Belastung
weder auseinanderklaffen
noch sich durchdringen
Die Verschiebungsvektoren und deren
Komponenten sind stetige Funktionen
Modellierung von Zellstrukturen
16
Modellierung von Zellstrukturen
Kompatibilitätsbedingung:
Benachbarte materielle Teile
werden nach Belastung
weder auseinanderklaffen
noch sich durchdringen
u=u(x,y,z,t)=ux(x,y,z,t)ex+uy(x,y,z,t)ey+uz(x,y,z,t)ez
Modellierung von Zellstrukturen
17
Modellierung von Zellstrukturen
C
D
u(x+dx,y,dy,z)
u(x,y+dy,z)
u(x+dx,y,z)
B
A
u(x,y,z)
A1
B1
ux(x+dx,y,z)=ux(x,y,z)+(ux(x,y,z)/ x)dx
Modellierung von Zellstrukturen
18
Kinematisches Gleichgewicht
x = u/x
u v w
y = v/y
z = w/z
xy = v/x + u/y
xz = w/x + u/z
yz = w/x + v/z
Modellierung von Zellstrukturen
19
Modellierung von Zellstrukturen
Kompatibilitätsbedingung:
iklm= 0
Riemann
Modellierung von Zellstrukturen
Tensor 4. Stufe
20
Modellierung von Zellstrukturen
Stoffgesetze:
1-starres Material
2-linear-elastisch
3-nichtlinear-elast.
4-linear-elastisch-idealplastisch
5-starr-plastisch
6-viskoses Material:
Kriechen
7-viskoses Material:
Relaxieren
σ
5
4
2
1
3
6
7
ε
Modellierung von Zellstrukturen
21
Modellierung von Zellstrukturen
Stoffgesetze:
S , S   , 
Verzerrungstensor
Verzerrungsgeschwindigkeit
Spannungstensor
Spannungsgeschwindigkeit
Modellierung von Zellstrukturen
22
Modellierung von Zellstrukturen
Elastisches
Materialverhalten
S 
Stoffe ohne Gedächtnis
Verzerrungstensor
Spannungstensor
Modellierung von Zellstrukturen
23
Modellierung von Zellstrukturen
plastisches
Materialverhalten
Stoffe mit permanentem
Gedächtnis
S  
Verzerrungsgeschwindigkeit
Spannungsgeschwindigkeit
Modellierung von Zellstrukturen
24
Modellierung von Zellstrukturen
viskoses
Materialverhalten
S  
Stoffe mit schwindendem
Gedächtnis
Verzerrungsgeschwindigkeit
Spannungstensor
Modellierung von Zellstrukturen
25
Modellierung von Zellstrukturen
Biologische Systeme und
Zellstrukturen sind in der
Regel:
Nichtlinear, anisotrop, inhomogen
Zylindrische Anisotropie –
Blutgefäße
Biologische Systeme zeigen ein
elastisch bis viskoses Verhalten
und können alle
Zwischenstadien einnehmen
Zellen sind dynamische Systeme
Aggregationsprozesse
Dis
Modellierung von Zellstrukturen
26
Modellierung von Zellstrukturen
Zellen, Zellstrukturen

dynamische Strukturen
Spontane Aggregationsprozesse
Skelettfilamente
Spontane Abbauprozesse
extrazelluläre Matrix
Frequenzabhängige Materialeigenschaften
Versuche zwingend erforderlich
Modellierung von Zellstrukturen
27
Modellierung von Zellstrukturen
Näherungsverfahren:
Diskretisieren
des Zellen und der Zellstrukturen
des Materialverhaltens
der Belastungsfunktionen
der Zeit, direkte Zeitintegration
Modellierung von Zellstrukturen
28