Present_lec3_propag_2009

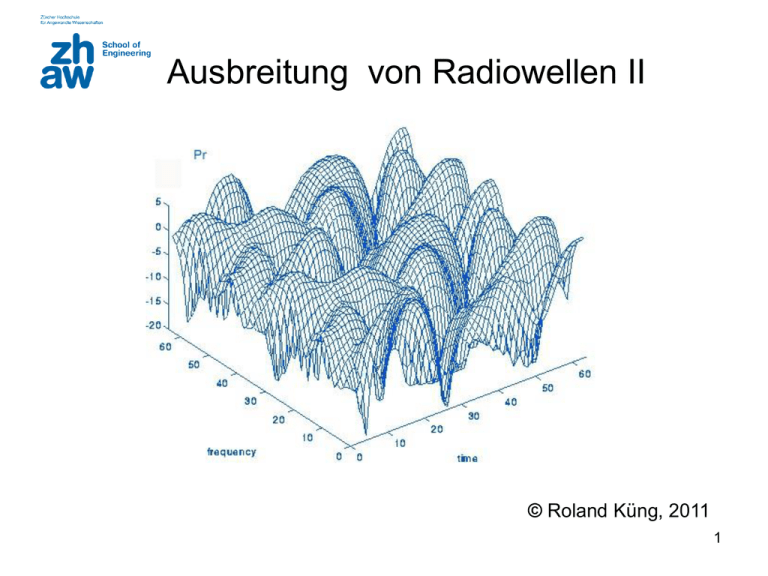
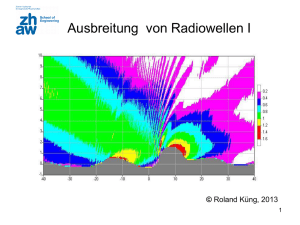
Ausbreitung von Radiowellen II
© Roland Küng, 2011
1
Realität: Mehrwegausbreitung
• Mehrere Reflexionen, Beugungen und Streuungen gleichzeitig
• TX, RX oder Hindernisse bewegen sich
2
Large Scale - Small Scale Modelle
• Addition aller Beträge führt zu Signalschwund (Fading)
• Glättung der Messwerte über kleine Verschiebungen
–  Large Scale Modelle, verfeinert um Statistik
– Wichtig für mittlere Distanzbestimmung
• Fluktuation über kleine Verschiebungen
–  Small Scale Modell
– Wichtig für max. Bandbreite und min. Symbolrate
3
Modell “Exponent n”
• Anpassung des Exponenten n bei der Kanaldämpfung im Term dn
Kanaldämpfung [dB]:
darin Teil Sichtverbindung bis do [dB]:
 d 
PLpath (d)  PL f s(do)  10  n  log 
 do 
 4  do 
PL f s(do)  10  log

  
2
Messtechnischer Ansatz [dBm]:
 d 
Pr (d)  Pf s(do)  10  n  log 
 do 
darin Teil Sichtverbindung bis do [dBm]:
Messwert bei do
oder Rechenwert [dBm]:
 Pt G t Gr 2 
  30
Pf s(do)  10  log
2
2 
 ( 4) do 
Note: fs = freespace
4
Modell “Exponent n”: do und 
Einsatzort
Indoor Office
Indoor Factory
Outdoor Urban
Outdoor Rural
do
1m
10 m
100 m
1000 m
Beispiel: n = 3.8
do
RFprop3*
*Prop Tool auf
https://home.zhaw.ch/~kunr/ntm.html
unter Praktikum 1
5
Indoor Messungen für n und 
•
Wegen statistischen Schwankungen über die Orte (Large Scale), muss auch
die Streuung  von Pr(d) ermittelt werden (Log-normal Verteilung: dB, dBm)
•
Für Verbindungssicherheit ist dann eine Marge X [dB] einzurechnen
PLpath
Pr(d)
X
Prob of missing
Empfangssignal in dBm:
 d 
PXr (d)  Pr (do)  10  n  log   X 
 do 
6
Was bedeutet die Streuung ?
Die Wahrscheinlichkeit, dass ein Empfangspegel PXr den Wert  überschreitet beträgt:
 X 
   Pr (d) 
WSK PXr (d)     Q 

1

Q
 




 
Q-Funktion
PDF
Pr(d)= Pr(do)-10·n·log(d/do) (Mittelwert)
Std. Abweichung  :
84.1% der Pegel im Intervall m- bis ∞
97.7% im Intervall m-2 bis ∞
99.9% im Intervall m-3 bis ∞

Min. Empfangssignal [dBm] für bestimmte WSK:
 d 
  Pr (do)  10  n  log   X
 do 
: Schwelle/Empfindlichkeit [dBm]
Pr(d): mittlerer Empfangspegel [dBm]
X = P r(d) - : Fading Marge [dB]
z.B
X = - (-Pr)

Pr
PXr
7
Was bedeutet die Streuung ?
Beispiele
1
Pr(d) = -60 dBm, Marge X = 10 dB
Streuung  = 10 dB, WSK für Empfang ?
Sensitivity RX  = -70 dBm
Q(-10/10) = Q(-1) = 1-Q(1) = 1-0.159 = 0.841
d.h. mit WSK 84.1% ist PXr(d)>-70 dBm
Mit 15.9% ist der Empfangspegel kleiner als die Schwelle 
2
Pr(d) = -60 dBm, WSK für Empfang = 88.5%
Streuung  = 12 dB, notwendige Marge?
Q(-z) = 0.885, Q(z) = 1-Q(-z) = 0.115 liefert z =1.2
Marge X = 12·1.2 = 14.4 dB
Mit Schwelle  = -74.4 dBm ist WSK für Empfang 88.5%
z
0
Q(-z) = 1-Q(z)
8
Indoor Absorptionen
 Dämpfung durch Absorption Labsorb
[dB]
Empfangssignal in dBm:
 d 
Pr (d)  Pr (do)  10  n  log   L absorb  X 
 do 
9
Empirische Modelle
z.B COST-231 Hata Modell
http://en.wikipedia.org/wiki/COST_Hata_model
Hata Modell für Mobilfunk gilt gut unter
folgenden Randbedingungen:
f = 1500 MHz bis 2500 MHz,
ht = 30 m bis 200 m,
hr = 1 m bis 10 m
d = 1 km bis 20 km
Medianwert Pfad Dämpfung (Path Loss):
PL50  46.3  33.9  log( fc )  13.82  log(ht )  a(hr )  (44.9  6.55  log(ht )) log( d)
a(hr )  (1.1 log( fc )  0.7)hr  (1.56  log( fc )  0.8)
Note: d in km, f in MHz)
10
Small Scale Model – Fading Kanal
Subtraktion des Large Scale Effekts
Antennenverschiebung
Antennenverschiebung oder Verweilzeit
11
Ursache des Small Scale Fading:
Bewegung und Mehrweg
 Solange nur 1 Pfad existiert passiert nichts spezielles
 Änderung Phasenlage
 
2l 2vt

cos 


Einzelner Pfad von vielen
 Frequenzverschiebung (Doppler)
fd 
v
 cos 

Bei bewegtem Mehrweg ergeben sich 3 Effekte:
•
•
•
Lage der E-Feldvektoren ändern räumlich
Doppler Kopien durch unterschiedliche Geschwindigkeiten (Frequency Dispersion)
Zeitliche Echos durch unterschiedliche Laufzeiten (Time Dispersion)
12
Wirkungen bei Mehrweg
H
Bewegung
Echo
h
t
f
H,
m(t)cos(t)
=0
f
t
Doppler Shift
Delay e-j
H
h

fd
t
f
Sum of both
Sum of both
Nullstellen @
f0=k/2, k odd
H,
m(t)cos(t) + m(t)cos((+d)t)
f
t
=
13
Zeitliche Schwankung: Case 1
Grosse Zahl Pfade mit Doppler aber irrelevant geringen Laufzeitunterschieden:
Modell: LOS: Rice Verteilung der Amplitude NLOS: Rayleigh Verteilung (A=0)
u(t), v(t): AWGN A Amplitude LOS
Schmalbandfunk kbit/s
Slow or Fast Fading
14
Zeitliche Schwankung: Case 1
•
Wegen statistischen Schwankungen über die Zeit, muss eine Marge Y [dB]
eingerechnet werden (i.A. nicht Gauss sondern Rayleigh oder Rice verteilt)
X
Y
Note: nur für schmalbandige Signale (Delay Spread irrelevant / Flat Channel) sinnvoll
15
Mehrweg Empfang: Case 2
Anzahl Pfade mit Laufzeitunterschieden aber irrelevant kleinen Dopplerunterschieden
Modell: Tapped Delay Line
Breitbandfunk Mbit/s
_i Delay, a_i Amplitude
Flat or Frequency-Selective Fading
16
Beschreibung mit Mehrweg-Modell
 Am besten beschrieben durch:
Stossantwort = Multipath Impulse Response
Power [dBm]
Line of Sight LOS
Multipath Components (NLOS)
Reflexionen Zugerberg
Reflexionen Rigi
Basisstation Cham
Delay [ns]
17
Mehrweg-Profil in Raum und Zeit
E-Field
Allgemeine Beschreibung.
sehr komplex
MOVEMENT IN m
Delay
18
Mehrweg formt Frequenzgang Bewegung verändert ihn
19
Vereinfachtes Mehrweg-Modell
Für max. Bandbreite von B 
1
bei Frequenz fc
2  
vereinfacht man die Beschreibung von h(t,) im Basisband:
 Es existieren N diskrete Pfade mit i  i  
 h( t, ) 
N1
i  0... N  1
N1
 c (t )  (   (t ))   a (t ) exp[ j(2f  (t )   (t ))]  (   (t ))
i
i0
i
i
c i
i
i
i0
h(t, )
Phase
Amplitude
Delay gegenüber LOS
d.h. Excess Delay
Mehrweg
20
Charakterisierung Mehrwegkanal
Aus der Stossantwort des Kanals
ergibt sich das Power Delay Profile
Pi  ai
2
Stochastik liefert:
LOS
Der RMS Delay Spread beschreibt den
Kanal bezüglich Mehrweg mit einer
einzigen Grösse.
21
Bsp.: Power Delay Profile
Pr()
4.38 µs
1.37 µs
1.37 µs
0 dB
-10 dB
-20 dB
-30 dB

0
1
2
5
Excess Delay
(µs)
  (1)(5)(0.1)(1)(0.1)(2)(0.01)(0)  4.38s
_
[0.010.10.11]
_
2
 
(1)(5) 2 (0.1)(1) 2 (0.1)(2) 2 (0.01)(0) 2
[0.010.10.11]
  21.07(4.38)2 1.37s
 21.07s 2
22
RMS Delay Spread: Typical values
Der RMS Delay Spread ist ein gutes Mass für den Mehrwegkanal
Urban
Swiss GSM
Industrial Site
Suburban
ZHAW Lab
Building
Office Building
10ns
50ns
150ns
3m
15m
45m
500ns
1µs
150m 300m
2µs
600m
5µs
10µs
3Km
25µs
7.5Km
23
LTE Fading Models
Source:
ETSI, TS 136101 Annex B, 2011
24
Symbolbandbreite BS versus Kanal
BS < BC
Mass der Dinge ist die
Kohärenzbandbreite Bc
The coherence bandwidth of a
wireless channel is the range
of frequencies that are allowed
to pass through the
channel without distortion.
BS > BC
25
Flat  Frequency-Selective Fading
Flat
Symbol x
Näherung für Kohärenzbandbreite BC
1
Bc 
2   
Frequency-Selective
Symbol x
Frequency
Time
Bandbreite für Symbole:
BS < BC  Flat
BS > BC  Frequency-Selective
Frequency
Time
Wichtig für die Symbol Detektion !
26
Symboldauer TS versus Kanal
wie rasch ändert der Kanal
Channel x
Slow
Mass der Dinge ist die Kohärenzzeit Tc
Tc 
0 .4
fm
fm = max. Doppler fmax 
v max

Channel x
Frequency
Fast
Time
Dauer für 1 Symbol:
TS < TC  Slow Fading
TS > TC  Fast Fading
Frequency
Wichtig für die AGC (Pegelregelung) !
Time
27
Slow Fast Fading
Im Zeitbereich
28
Slow Flat  Slow Frequency Selective
Fading
Bei Freq. Sel. Fading
fehlen spektrale Anteile.
Dies heisst Verzerrungen!
29
Klassierung Small Scale Fading
Delay
Doppler
(Änderung
des Delay)
30
Wahl von Signalbandbreite und
Symboldauer
•Schmalband (GSM…)
•OFDM (WLAN .11a, 4G…)
•Spread Spectrum
(CDMA, UMTS, WLAN .11b)
•Equalizer-based SC (GSM)
31
Schmalbandsystem Breitbandsystem
 Schmalbandsystem: W < Bc
 Breitband: W > Bc
Bc
W
 Gegenmassnahme zum Kanaleinfluss:
 für Schmalbandsystem mit W < Bc: Diversity Frequenz, Zeit, Raum
 für Breitband mit W > Bc: Kanal Equalizer, Spread Spectrum, OFDM
32
Praktische Systeme
Wie gehen praktische Systeme mit Mehrweg Delay Spread um?
 Analoge Signalübertragung
 Digital Datenübertragung
 GSM
 DECT
 IS95 (USA)
 UMTS
Schmalband: B < Bc
Diversity Zeit, Frequenz, Raum
Adaptiver Equalizer mit
Trainingssequenz für Kanalschätzung
Diversity, nur in Small Delay Umgebung
RAKE Empf. Spread Spectrum
1.2 Mchip/s Length 128 chip/bit
RAKE Empfänger Spread Spectrum
3.84Mchip/s Lenght 4…512
chip/bit
 Digital Audio Broadcasting
WLAN 802.11a
OFDM Multi-Träger Modulation
Kanal aufgesplittet in Subbänder mit B < Bc
33
Mehrwegkanal bestimmt Bandbreite
Der Kanal lässt eine nutzbare Bandbreite Bc zu  max. Symbolrate
Ausnahmen (Breitbandsysteme):
 Spread Spectrum Technik mit RAKE Empfänger zum Einzelempfang
jedes verzögerten Pfades (Lecture 11)
 OFDM, Daten auf je 1 Träger in mehrere Kanäle der Breite <Bc verteilen
(Lecture 10)
Bc 
1
2   
34
Inter Symbol Interference (ISI)
 =1.4 µs
Pr()
Symbol time
0 dB
-10 dB
-20 dB
-30 dB


0
1
2
5
4.4 µs
(µs)
0
1 2
5
(µs)
mean = 4.4 µs
Erfahrungswert:
Symbol time > 10·
--- No ISI, no equalization required, ev. Guard Interval*
Symbol time < 10·
--- ISI, Equalization* will be required to deal with ISI
Im Beispiel sollte Symboldauer > 14 µs sein um ISI zu vermeiden.
d.h. die Symbolrate < 70 kbps (approx)
*Note: NTM2
35
Diversity gegen Slow Fading
 Time Diversity : Dank Doppler ändert die Situation mit der Zeit
 Kopie senden nach Kohärenz-Zeit TC
 Frequency Diversity: Mehrweg wirkt nicht bei allen Frequenzen Flat
Kopie senden in Kanal mit Abstand > Kohärenzbandbreite BC
 Antenna Diversity: Örtlich ist die Situation verschieden (Abstand > /2)
Interleaving: Zusätzliche Massnahme Datenverschachtelung plus Fehlerkorrektur
38
Design-Freiheiten
Distanz
Sendeleistung
Kanaleigenschaften
Funkzulassung
Frequenz
Bitrate
Rauschzahl
Empfindlichkeit
Bandbreite
Fehlerrate (QOS)
Modulation
frei: Quellenkodierung, Fehlerschutz, Beam Forming, Repeater
39