Der Millikan-Versuch (Gleichfeldmethode) - Leibniz

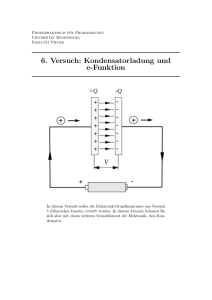
Der Millikan-Versuch
(Gleichfeldmethode)
Facharbeit im Leistungskurs Physik
Bearbeitender Schüler: Alexander Zouari
Betreuender Fachlehrer: Herr Littig
02.06.2006
© Alexander Zouari 2006
Der Millikan-Versuch
(Gleichfeldmethode)
Gliederung:
1. Einleitung
2. Versuchsaufbau
2.1 Stromversorgung des Kondensators
2.2 Stromversorgung der Lampe und der Relais
2.3 Anschluss der Zeitmesser
3. Eichung des Okularmikrometers
4. Versuchsdurchführung / Film
5. Herleitung der benötigten Formel
6. Berechnung von Q
© Alexander Zouari 2006
Der Millikan-Versuch
(Gleichfeldmethode)
1. Einleitung
Mit dem Millikan-Versuch wird die Elementarladung e
bestimmt. In den Millikankondensator werden geladene
Öltröpfchen eingesprüht. Den Kondensator kann man
umpolen und durch die Fall- und Steiggeschwindigkeit der
Öltröpfchen kann man mithilfe einer Formel die
Elementarladung e ausrechnen.
Für die genaue Berechnung der elektrischen Ladung e
anhand dieses Versuchs erhielt Dr. Robert A. Millikan im Jahr
1923 den Nobelpreis für Physik.
© Alexander Zouari 2006
Zeitmesser 1
Kondensatorspannung
Versuchsaufbau
Lampe
Kondensator
Mikroskop
Spannungsquelle
für die Lampe
Zeitmesser 2
Umpolvorrichtung
Spannungsquelle
für Kondensator
und Relais
© Alexander Zouari 2006
© Alexander Zouari 2006
Aufsatz zum
Einsprühen der
Öltröpfchen
Lampe
Kondensator
Mikroskop
© Alexander Zouari 2006
2.1 Stromversorgung des Kondensators
8
7
3
6
4
5
Die Spannungsquelle (3) liefert die für den Kondensator benötigte Spannung. Von
der Spannungsquelle wird der Strom über die Eingangsbuchse (4) in die
Umpolvorrichtung geleitet. Mit dem Hebel (5) kann man den Kondensator umpolen.
Von der Ausgangsbuchse (6) der Umpolvorrichtung fließt der Strom zu dem
Kondensator (7). Die an dem Kondensator angelegte Spannung wird mit dem
Spannungsmessgerät (8) gemessen.
© Alexander Zouari
2.2 Stromversorgung der Lampe und der Relais
3
10
12
9
5
11
Beim Umpolen des Kondensators mit dem Hebel (5) werden zwei Relais betätigt.
Diese werden mit dem schwarzem Kabel (9), das mit der Spannungsquelle (3)
verbunden ist, mit Strom versorgt. Die Lampe (10) muss ebenfalls mit Strom
versorgt werden. Sie ist mit dem weißem Kabel (11) an einer separaten
Spannungsquelle (12) angeschlossen.
© Alexander Zouari 2006
2.3 Anschluss der Zeitmesser
1
2
14
13
5
Der Zeitmesser 1 (1) ist mit dem roten Kabel (13), der Zeitmesser 2 (2) mit dem
gelben Kabel (14) mit der Umpolvorrichtung verbunden. Beim Schalten des Hebels
(5) nach oben wird an dem Kondenstor die eingestellte Spannung so angelegt, dass
oben die Anode liegt. Beim Umlegen des Hebels nach unten wird der Kondensator so
umgepolt, dass die Anode unten liegt. Dabei misst der Zeitmesser 1 wie lange die
Anode oben und der Zeitmesser 2 wie lange die Anode unten ist.
© Alexander Zouari 2006
3. Eichung des Okularmikrometers
Damit man die Strecke, die die Öltröpfchen zurücklegen,
messen kann, muss man in einem Vorversuch die
Unterteilungen des Okularmikrometers des Mikroskops mit
einem Objektmikrometer bestimmen.
Okularmikrometer
Objektmikrometer Die Unterteilung des
Objektmikrometers
(helle Striche) beträgt
ein hundertstel
Millimeter. Daraus folgt,
dass die schwarzen
Striche des
Okularmikrometers etwa
0,025 mm voneinander
entfernt sind.
© Alexander Zouari 2006
4. Versuchsdurchführung
Zum Einbringen geladener Öltröpfchen wird ein Zerstäuber
benutzt. Der Zerstäuber wird mit Paraffinöl gefüllt und an
den Einlass des Aufsatzes zum Einsprühen der Öltröpfchen
gehalten. Bei dem Einsprühen laden sich die Öltröpfchen
durch die Reibung an der Luft auf. Im Innern des Aufsatzes
entsteht ein Wirbel zur Mitte hin. Im Boden befindet sich
eine Bohrung, durch die die Öltröpfchen in das Innere des
Kondensators gelangen. Nach dem Einsprühen der
geladenen Öltröpfchen schaut man durch das Mikroskop,
wählt ein gut sichtbares Öltröpfchen aus und bestimmt zwei
Markierungen auf dem Okularmikrometer, zwischen denen
sich das Öltröpfchen auf und ab bewegen soll.
© Alexander Zouari 2006
4. Versuchsdurchführung
Das Öltröpfchen sinkt wegen der Erdanziehungskraft, ohne
dass ein elektrisches Feld vorhanden ist (Achtung!: Durch
das Mikroskop ist oben und unten vertauscht!). Wenn das
Öltröpfchen eine Markierung erreicht, wird mithilfe der
Umpolverrichtung das elektrische Feld eingeschaltet. Wenn
das Öltröpfchen die andere Markierung erreicht, wird der
Hebel umgelegt, d.h. das Feld wird umgepolt. Diesen
Vorgang wiederholt man einige Male und stoppt dabei die
Steig- und Fallzeiten. Durch das Mikroskop sieht das wie
folgt aus .....
© Alexander Zouari 2006
© Alexander Zouari 2006
5. Herleitung der benötigten Formel
Wir haben zunächst zwei Bewegungen zu betrachten: die Sink- und die
Steigbewegung. Wenn das Öltröpfchen sinkt, dann wirken elektrische Kraft und
Gewichtskraft in die gleiche Richtung, d.h. wir können ihre Beträge addieren, um
eine resultierende Kraft zu erhalten:
Für den Steigvorgang gilt, dass die elektrische Kraft entgegengesetzt zur
Gewichtskraft wirkt, die beiden Kräfte also für eine resultierende Kraft subtrahiert
werden müssen:
© Alexander Zouari 2006
Beim Versuch ist zu beachten, dass es neben den anderen Kräften zusätzlich noch
eine Reibung gibt. Nach dem STOKES’schem Reibungsgesetz ergibt sich für diese
Kraft:
r der Radius des beobachteten Öltröpfchens und v die Geschwindigkeit des
Tropfens seien. Damit die Kraft, die das Tröpfchen bewegt, groß genug ist, muss
sie die Reibung aufwiegen können, für den Sinkvorgang bedeutet das also:
v1 ist hierbei die Sinkgeschwindigkeit. Für die Steiggeschwindigkeit v2 gilt:
© Alexander Zouari 2006
Unser Ziel ist es, Q zu berechnen. Dazu haben wir noch relativ viele
Unbekannte und außerdem noch keinen Zusammenhang zwischen den
beiden Geschwindigkeiten. Deshalb werden wir v1 und v2 addieren, und
dann subtrahieren:
© Alexander Zouari 2006
Beide Gleichungen enthalten den Radius der Öltröpfchen, der uns aber
nicht bekannt ist. Daher stellen wir beide Gleichungen nach r um und
setzen sie anschließend gleich, sodass r aus beiden eliminiert wird:
© Alexander Zouari 2006
Wir behalten weiterhin das Ziel im Auge, Q zu ermitteln und formen
deshalb danach um:
© Alexander Zouari 2006
Da auch E nicht bekannt ist, ersetzen wir es durch
wobei d der Plattenabstand des elektrischen Feldes ist (d = 2,5 mm) und U die
angelegte Spannung (U = 250 V):
Weiterhin ist die Masse m eines Öltröpfchens unbekannt. Ein Öltröpfchen ist relativ
schwer zu wiegen, was es notwendig macht, die Masse aus der Gleichung zu
eliminieren. Die Dichte von Öl ist jedoch bekannt, womit es sinnvoll ist, damit zu
rechnen:
Bei den Tröpfchen gehen wir davon aus, dass sie die Form einer Kugel haben,
womit das Problem des Volumens (fast) behoben wäre:
Daraus folgt für Q:
© Alexander Zouari 2006
Da uns immer noch nicht bekannt ist, wie der Radius des
Öltröpfchens lautet, übernehmen wir die Formel von oben für r:
© Alexander Zouari 2006
Wir teilen nun durch Q³, damit wir alle Q auf eine Seite bekommen,
und erhalten:
E ist uns immer noch nicht bekannt, da wir aber weiterhin wissen,
dass
ist, erhalten wir:
© Alexander Zouari 2006
6. Berechnung von Q
Das Öltröpfchen bewegt sich zwischen 24 Unterteilungen des Okularmikrometers achtmal hoch
und achtmal runter. Der Abstand zwischen zwei Unterteilungen beträgt 0,025 mm. Die zurück
gelegte Strecke beträgt somit:
=> 24 . 0,025 mm = 0,6 mm = 0,0006 m
Benötigte Zeit für das
achtmalige Sinken des
Öltröpfchen (29,4 s)
Benötigte Zeit für das
achtmalige Steigen des
Öltröpfchen (34,1 s)
-19
=>
1,70 . 10 C
29,4 s : 8 = 3,657 s
v1 =
0,0006 m
3,657 s
-4
.
= 1,63 10
m
s
34,1 s : 8 = 4,2625 s
v2 =
0,0006 m
4,2625 s
= 1,41 . 10
-4
m
s
-19
.
Literaturwert: Q = 1,6021892 10 C
Der berechnete Wert Q weicht aufgrund von Messungenauigkeiten minimal vom Literaturwert ab.
© Alexander Zouari 2006