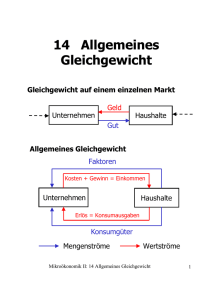
Ausgehandelte Tauschrelation

8.
A:
Zwei Wirtschaftssubjekte, A und B, arbeiten jeweils 10
Stunden pro Tag. In dieser Zeit kann A maximal 84
Mengeneinheiten (ME) von Gut 1 oder 72 ME von Gut 2
herstellen; für B lauten die maximalen Outputs 36 ME von
Gut 1 oder 60 ME von Gut 2.
a) Definieren und quantifizieren Sie: Arbeitskoeffizienten,
Arbeitsproduktivitäten, absolute Kostenvorteile.
Arbeitskoeffizienten: Arbeitsleistung pro ME Output
10  h 
a1=
84  ME 
b1=
10
36
10  h 
a2= 
72  ME 
b2=
10
60
Arbeitsproduktivität: Output pro ME Arbeitsleistung
1 84  ME 

a1 10  h 
1 36

b1 10
1 72

a2 10
1 60

b2 10
Absolute Kostenvorteile : geringerer Arbeitsaufwand pro
ME von Gut i bei einem WiSu als beim anderem WiSu
10
10
a1=
< b1=
Absoluter Kostenvorteil für WiSu A
36
84
1
84
1 36

Absoluter Produktivitätsvorteil für WiSu A
> 
a1 10
b1 10
10
10
a2=
< b2=
Absoluter Kostenvorteil für WiSu A
72
60
1
72
1 60

Absoluter Produktivitätsvorteil für WiSu A
> 
a2 10 b2 10
A:
b) Berechnen, interpretieren und veranschaulichen Sie
grafisch: Gleichung der Produktionsmöglichkeiten,
Transformationskurve, Opportunitätskosten, relative
(komparative) Kostenvorteile.
Gleichung der Produktionsmöglichkeiten:
Arbeitseinsatz
Arbeitseinsatz
Verfügbare
+
=
Bei Gut 1
Bei Gut 2
Arbeitsmenge
Gleichung gibt die maximal mögliche Produktionsmengen
an.
A
A
A
L

X
a1 1
+ a2  X 2
=
 h 


 ME1 
ME1 
[h]
10
 X1A
84
 h 
+  ME 

2
+
ME2 
[h]
10
 XA
2
72
=
[h]
=
10
Interpretation: Gleichung gibt diejenigen MengenkomA
bination von X1A und X2 an, die WiSu A mit seinen
verfügbaren Produktionsfaktoren maximal bestellen kann.
Beispiele für solche Outputkombinationen:
WiSu A:
A
X1A  0 X2  72
A
X
XA

0
1  84
2
vollständige
Spezialisierung
WiSu B:
10
 X1B
36
+
10
 XB
2
60
=
10
Kurve der Produktionsmöglichkeiten:
Geometrischer Ort aller Kombinationen von X1 und X 2 ,
Das WiSu maximal produzieren kann.
X1A
vollst. Spezial.
84
Für WiSu A
vollst. Spezial.
72

XA
2
Die Steigung der Kurve zeigt, wie sich durch andere
Aufteilung der Arbeitszeit ME von Gut 1 in ME von Gut 2
transformieren lassen
X1B
Für WiSu B
vollst. Spezial.
36
vollst. Spezial.
60
XB
2
X1A
84
A
Bsp. WiSu A will X2 um 1 ME erhöhen:
 Pfeil nach rechts
10
 hierfür benötigt es
72
Stunden Arbeit:
XA =1
2
X1A  1.2
72

XA
2
10
 a2 = 1 
72
 diese Zeit muss aus der Prod.
A
X
von 1 abgezogen werden, so
A
dass die Prod. von X1 sinkt um
XA
2
X1A

 10  84
  1
 1.2

 72  10
X A2
1
A a2
 a2   X 2 
a1
a1
Zahl d. Dienstsstunden, die zur
ME von Gut 1, die man pro
A
Mehrproduktion von X 2 benötigt Stunde, die jetzt weggenommen wird, erzeugt hat
A
A
X
X
Wir erkennen: es kostet Prod.-einbußen bei
1, wenn
2
erhöht werden soll.
Der Quotient
X1A 1.2

 1.2
A
1
X 2
bezeichnet:
- ökonomisch die Opportunitätskosten von Gut 2
X1A
  tan 
- grafisch die Steigung der Transformationskurve:
A
X2
Der Quotient lässt sich erkennen an der Gleichung der
Produktionsmöglichkeit:
10
10 72 A L a2 A
X1A 

X2   X2
10 10
a1 a1
84 84
In infinitesimaler Form:
Für WiSu B:
dX1A
84
a2
     1.2
A
72
a1
dX2
dX1B
36
b2
     0.6
B
60
b1
dX2
Ergebnis: WiSu B hat komparative (relative) Kostenvorteile
bei Gut 2, d.h. die Prod.-einbußen bei Gut 1 sind kleiner als
bei WiSu A, wenn Gut 2 um 1 ME mehr produziert wird
c) Erläutern Sie die Vorteile der Spezialisierung für die
Gesamtwirtschaft und veranschaulichen Sie diese grafisch
A:
WiSu A: senkt
XA2 um 1 ME
erhöht X1A um 1.2 ME
WiSu b: erhöht X B2
um 1 ME
senkt X1B um 0.6 ME
Gesamtwirtschaft:
- X 2 konstant (1 – 1) = 0
- X1 um (1.2 – 0.6) = 0.6 ME gestiegen
Basis für gesamtwirtschaftl. Prod.zuwachs:
Erstens:
dX1A
 1.2
A
dX 2
>
dX1B
 0.6
B
dX 2
d.h. unterschiedliche Opp.kosten
Zweitens: Richtige Spezialisierung
d.h. WiSu A spezialisiert sich auf Gut 1, WiSu B
auf Gut 2
Angenommen:
WiSu A spezialisiert sich völlig auf X1: X1 =X1A = 84  Punkt Y
WiSu B völlig auf X 2 : X2 =XB2 = 60  Punkt Z
Verschiebung:
X1
- der Trans.Kurve des B nach oben
- der Trans.Kurve des A nach rechts
120 K
84
Y
 gesamtwirtschaftl. Transf.Kurve:
G
36
Z
60
72
• Punkt G: gesamtw. Prod.Mengen
bei volls. (richtiger) Spez.
• Punkt H: Beide Sektoren spezial.
sich auf X 2
• Punkt K: Beide Sektoren spezial.
sich auf X1
H
132 X 2
Angenommen:
Beide spezialisieren sich falsch:
X1 =X1B max =36
max
X2 =XA
=72
2
X1
 Punkt T

liegt unterhalb d. Prod.Mögl.
bei richtiger Spezialisierung
K
84
Y
G
T
36
Z
60
H
72
X2
d) Erläutern und veranschaulichen Sie grafisch die
Vorteilhaftigkeit der Spezialisierung für A und B, wenn sich
beide auf eine Tauschrelation von 0,8 ME Gut 1 pro ME
Gut 2 einigen
A: Ausgangspunkt: Wenn A u. B das gesamtwirtschaftl.
Sinnvolle (=vollständige Spezialisierung) tun sollen, dann
- müssen sie das jeweils andere Gut vom „Spezialisten“
eintauschen und,
- dabei einen Vorteil gegenüber der Eigenproduktion
aufweisen.
Dies ist gewährleistet, wenn
- sie tauschen und
- sich dabei auf eine Tauschrelation einigen, die
betragsmäßig zwischen ihren Opp.Kosten liegt:
A
A
B
X
dX1
dX
1  B
1

0.8

1.2
 0.6
B
>
>
A
B
A  X2
dX 2
dX 2
Ausgehandelte Tauschrelation
Vorteilhaftigkeit für A:
Angenommen, A möchte 1 ME von Gut 2 mehr haben,
hierfür 2 Möglichkeiten:
- Selbstprod.: Kosten in Form von Opp.Kosten von 1.2
ME von Gut 1
- Bezug von B: Kosten in Form von Tauschkosten in
Höhe von 0.8 ME von Gut 1
- Fazit: für A günstiger, X 2nicht selbst zu produzieren
und dafür X1-Prod. unverändert zu lassen und X 2
von B zu kaufen
Vorteilhaftigkeit für B:
- Wenn B die X 2-Prod. um 1 ME reduziert, kann es in der
eingesparten Arbeitszeit 0.6 ME X1 selbst produzieren
- Wenn B X 2-Prod. unverändert lässt und 1 ME von Gut
2 an A gibt, erhält er ein Tausch von A 0.8 ME von X1
Grafisch lässt sich die Vorteilhaftigkeit veranschaulichen,
indem wir
- das Koordinatensystem des B um 180° drehen und
- an die Spezialisierungsmenge des A anlegen
X1A
Bmax
X
60= 2
O
XB
2
B
84
36
X1B
OA
72
XA
2
WiSu A:
X1A
Bmax
XB
2
60= X 2
84
Vorteil f. 68
60
A:
OA
E
F
20
OB
- will 20 ME von X 2 haben
(ausgehend von vollständig.
Spezialisierung)
- müsste dafür 20 ∙ 1,2 = 24 ME
von Gut 1 weniger produzieren
(Punkt F)
- kann die 10 ME durch Tausch
für 20∙0,8 = 16 ME von Gut 1
erhalten (Punkt E)
 Vorteil: 20∙0,4 = 8 ME von Gut1
16
36
X1B
72
XA
2
WiSu B:
- erhält von A für die 20 ME
von Gut 2, 16 ME von Gut 1
(Punkt E)
- Würde es die Prod. um 20 ME
von Gut 2 reduzieren, könnte
es nur 20∙0,6 = 12 ME von
Gut 1 herstellen (Punkt G)
X1A
 Vorteil: 20∙0,2 = 4 ME von Gut1
XB
2
Bmax
60= X 2
84
G
68
E
60
F
OA
20
OB
12 Vorteil f. B
16
36
X1B
72
XA
2