14 Allgemeines Gleichgewicht

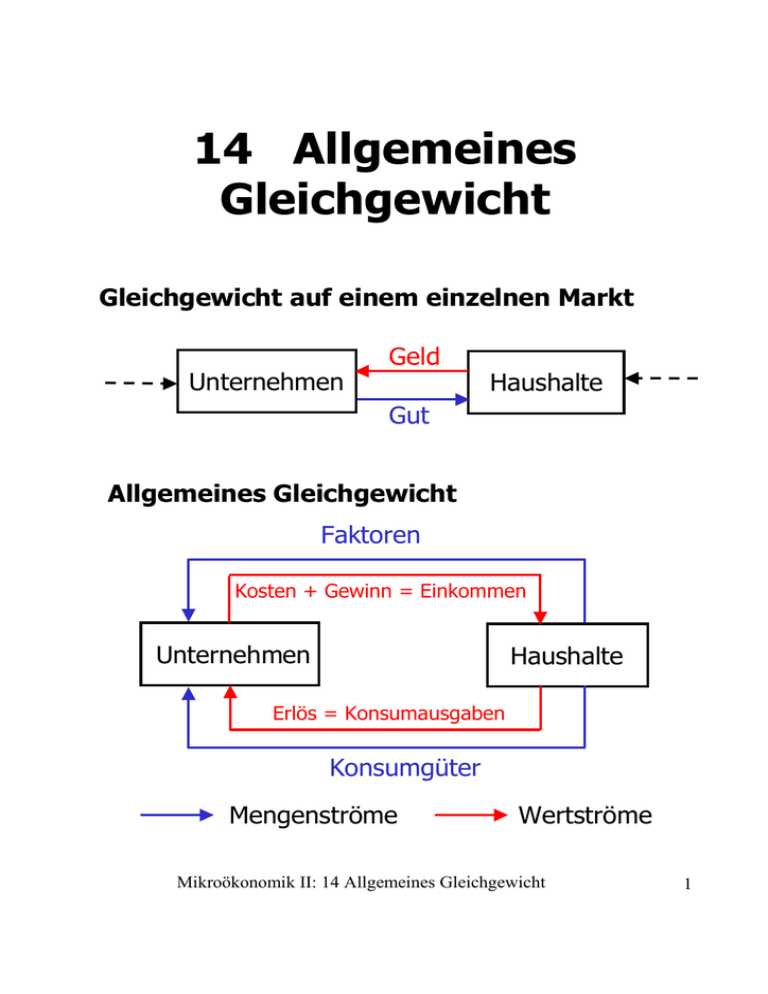
14 Allgemeines
Gleichgewicht
Gleichgewicht auf einem einzelnen Markt
Unternehmen
Geld
Haushalte
Gut
Allgemeines Gleichgewicht
Faktoren
Kosten + Gewinn = Einkommen
Unternehmen
Haushalte
Erlös = Konsumausgaben
Konsumgüter
Mengenströme
Wertströme
Mikroökonomik II: 14 Allgemeines Gleichgewicht
1
In der Theorie des Gleichgewichts auf einem
einzelnen Markt wird nur ein Preis endogen
bestimmt; alle anderen Preise und das
Einkommen jedes Konsumenten sind exogen.
In der Theorie des allgemeinen Gleichgewichts
sind alle Preise endogen. Es wird ein simultanes
Gleichgewicht auf allen (Konsumgüter- und
Faktor-) Märkten bestimmt.
Reiner Tausch
Gut 2
Ausgaben für Gut 2
Haushalt A
Haushalt B
Ausgaben für Gut 1
Gut 1
Mikroökonomik II: 14 Allgemeines Gleichgewicht
2
2 Haushalte A, B
2 Güter 1, 2
Keine Produktion.
ω 1A
ω A2
Ausstattung des Haushalts A mit Gut 1
Ausstattung des Haushalts A mit Gut 2
ω 1B
ω B2
Ausstattung des Haushalts B mit Gut 2
x1A
Konsum des Haushalts A von Gut 1
x 2A
Konsum des Haushalts A von Gut 2
x1B
Konsum des Haushalts B von Gut 1
xB2
Konsum des Haushalts B von Gut 2
(x
1
A
Ausstattung des Haushalts B mit Gut 1
, x A2 , x1B , xB2
)
Allokation
x1A + x1B = ω1A + ω1B 
erreichbare Allokation
2
2
2
2 
und x A + xB = ω A + ωB 
Mikroökonomik II: 14 Allgemeines Gleichgewicht
3
Grafische Darstellung erreichbarer Allokationen
ω1B
x A2
OB
x1B
ω B2
ω A2
x1A
OA
ω1A
xB2
Edgeworth-Box
Mikroökonomik II: 14 Allgemeines Gleichgewicht
4
Pareto-Effizienz
u A (x1A , x A2 )
Nutzenfunktion
u B (x1B , x B2 )
Nutzenfunktion
des Haushalts A
des Haushalts B
Definition:
Eine erreichbare Allokation (x1A , x A2 , x1B , x B2 )
ist Pareto-effizient, wenn es keine erreichbare
Allokation (x 1A , x A2 , x B1 , x B2 ) gibt, so dass
u A ( x 1A , x A2 ) ≥ u A ( x1A , x 2A )
und u B ( x B1 , x B2 ) ≥ u A ( x1B , x B2 ),
mit mindestens einem „>“.
Mikroökonomik II: 14 Allgemeines Gleichgewicht
5
Gut 2
OB
Gut 1
Y
X
Gut 1
OA
Gut 2
Allokation X ist nicht Pareto-effizient. Wenn
Haushalt A etwas von Gut 1 an Haushalt B abgibt
und dafür etwas von Gut 2 von Haushalt B
bekommt (
), dann stellen sich beide besser.
Der rote Pfeil illustriert eine ParetoVerbesserung. Allokation Y ist Pareto-effizient.
Hier gilt MRSA = MRSB.
Mikroökonomik II: 14 Allgemeines Gleichgewicht
6
Die Menge aller Pareto-effizienten Allokationen heißt
Kontraktkurve.
Gut 2
0B
Gut 1
nt
o
K
ve
r
u
tk
k
a
r
Gut 1
0A
Gut 2
Soweit die Kontraktkurve im Inneren der
Edgeworth-Box verläuft (d.h., falls
x1A , x A2 , x1B , x B2 > 0 ), gilt auf ihr
∂u A (x1A , x A2 , ) / ∂x1A
∂u B (x1B , x B2 , ) / ∂x1B
.
=
∂u A (x1A , x A2 , ) / ∂x A2
∂u B (x1B , x B2 , ) / ∂x B2
MRSA = MRSB
Mikroökonomik II: 14 Allgemeines Gleichgewicht
7
Wettbewerbsgleichgewicht
p1
Preis für Gut 1
p2
Preis für Gut 2.
Jeder Haushalt maximiert seinen Nutzen unter
seiner Budgetbeschränkung. Das liefert die
Marshallschen Nachfragefunktionen beider
Haushalte nach beiden Gütern.
Im Gleichgewicht wird von jedem Gut soviel
nachgefragt, wie vorhanden ist.
Haushalt A :
max
1
2
xA , xA
u.d.B.
⇒
u A ( x1A , x A2 )
p1 x1A + p2 x A2 = p1ω 1A + p2ω A2
x1A ( p1 , p2 ; p1ω 1A + p2ω A2 )
x 2A ( p1 , p2 ; p1ω 1A + p2ω A2 )
Mikroökonomik II: 14 Allgemeines Gleichgewicht
8
Ebenso für Haushalt B:
x1B ( p1 , p2 ; p1ω 1B + p2ω B2 )
x B2 ( p1 , p2 ; p1ω 1B + p2ω B2 )
Definition des Gleichgewichts:
Preise p1 , p2 so dass die
Markträumungs-Bedingungen
*
*
x1A ( p1* , p2* ; p1*ω1A + p2*ω A2 ) + x1B ( p1* , p2* ; p1*ω1B + p2*ω B2 ) = ω1A + ω1B
und
x A2 ( p1* , p2* ; p1*ω1A + p2*ω A2 ) + xB2 ( p1* , p2* ; p1*ω1B + p2*ω B2 ) = ω A2 + ωB2
erfüllt sind.
Walras-Gleichgewicht,
Wettbewerbsgleichgewicht
Mikroökonomik II: 14 Allgemeines Gleichgewicht
9
Gesetz von Walras
Für alle Preise p1 , p 2 ist der Wert der
gesamtwirtschaftlichen Überschußnachfrage 0.
[
⋅ [x
p1 ⋅ x1A ( p1 , p2 ) + x1B ( p1 , p2 ) − ω 1A − ω 1B
+ p2
2
A
( p1 , p2 ) + x B2 ( p1 , p2 ) − ω A2 − ω B2
]
]=
0.
Beweis:
Die Nachfragefunktionen erfüllen die Budgetgleichungen.
Folgerung:
Wenn Markt 1 geräumt ist, dann muß auch Markt 2
geräumt sein.
Es genügt zur Bestimmung des Gleichgewichts,
einen der beiden Märkte zu betrachten.
Mikroökonomik II: 14 Allgemeines Gleichgewicht
10
Grafische Bestimmung des Wettbewerbsgleichgewichts
Schnittpunkt der Preiskonsumkurven (offer curves)
Gut 2
OB
Gut 1
Gleichgewicht
x A2 (⋅) − ω A2
Überschußnachfrage
des Hh A,
Gut 2
OCB
OCA
Ausstattung
p1*
− *
p2
OA
ω 1A − x1A (⋅)
Überschußangebot des
Hh A, Gut 1
Gut 1
Gut 2
Die rote Gerade ist die gemeinsame Budgetgerade beider Haushalte zum GleichgewichtsPreisverhältnis p1*/p2*.
Gestrichelte Kurven: Indifferenzkurven durch die
Gleichgewichts-Allokation.
Mikroökonomik II: 14 Allgemeines Gleichgewicht
11
Gleichgewicht und Pareto-Effizienz
Der erste Hauptsatz der Wohlfahrtsökonomik
Die Allokation jedes Wettbewerbsgleichgewichts ist
Pareto-effizient.
Beweis:
Es seien
(x1A , x A2 , x1B , xB2 )
die Allokation im
Gleichgewicht und p1* , p2* die Gleichgewichts-Preise.
Entgegen der Behauptung gebe es eine erreichbare
Allokation, die den einen besser und den anderen
nicht schlechter stellt. Dann gibt es auch eine
erreichbare Allokation (x 1A , x A2 , x B1 , x B2 ) , die beide
besser stellt, d.h.
u A (x 1A , x A2 ) > u A (x1A , x A2 )
und
u B (x B1 , x B2 ) > u B (x1B , x B2 ) .
Mikroökonomik II: 14 Allgemeines Gleichgewicht
12
Da Haushalt A das bessere Güterbündel ( x 1A , x A2 )
im Gleichgewicht nicht gewählt hat, konnte er es
sich nicht leisten:
p1 x 1A + p2 x A2 > p1ω 1A + p2ω A2 .
Ebenso Haushalt B:
p1 x B1 + p2 x B2 > p1ω 1B + p2ω B2 .
Addieren der beiden Ungleichungen liefert:
p1 (x 1A + x B1 − ω 1A − ω 1B ) + p2 (x A2 + x B2 − ω A2 − ω B2 ) > 0.
Die Preise sind positiv. Deshalb muß eine der
beiden Klammern positiv sein. Die Allokation
(x 1A , x A2 , xB1 , xB2 ) ist also nicht erreichbar.
Mikroökonomik II: 14 Allgemeines Gleichgewicht
13
Der zweite Hauptsatz der
Wohlfahrtsökonomik
Wenn alle Haushalte konvexe Präferenzen haben,
dann gibt es zu jeder Pareto-effizienten Allokation
eine Verteilung der Anfangsausstattung, so dass
diese Allokation ein Wettbewerbsgleichgewicht ist.
Gut 2
Gut 1
0B
Y
Pareto-effiziente Allokation
X
Gut 1
0A
Begründung:
Gut 2
Die gemeinsame |MRS| einer Pareto-effizienten
Allokation definiert das GleichgewichtsPreisverhältnis. Die Anfangsausstattung kann dann
beliebig auf der so erzeugten Budgetgeraden
gewählt werden, z. B. X oder Y.
Mikroökonomik II: 14 Allgemeines Gleichgewicht
14
Produktion
Bestandteile einer Produktionsökonomie
•
•
•
Anfangsausstattungen an Gütern und
Produktionsfaktoren
Technologiemengen der Unternehmen
Präferenzen der Haushalte
Erreichbare Allokationen
•
•
Jedes Unternehmen führt einen technisch
möglichen Produktionsplan aus.
Die ursprünglich vorhandene und die
produzierte Menge eines Gutes sind zusammen
so groß wie die konsumierte und die als Input
verwendete Menge dieses Gutes.
Mikroökonomik II: 14 Allgemeines Gleichgewicht
15
Effizienz
Pareto-effiziente Allokationen werden durch drei
Teilaspekte charakterisiert.
Tauschoptimum, effiziente Konsumstruktur
Es ist nicht möglich, durch Tausch der
vorhandenen Konsumgüter einen Haushalt besser
zu stellen ohne einen anderen schlechter zu
stellen (siehe Definition S. 5 dieses Kapitels).
Bedingung für jeweils zwei Haushalte A, B:
MRS des Haushalts A = MRS des Haushalts B
Produktionsmaximum
Es ist nicht möglich, mit den vorhandenen Inputs
mehr von einem Gut zu produzieren ohne von
einem andern Gut weniger zu produzieren.
Bedingung für jeweils zwei Unternehmen 1, 2:
TRS in Unternehmen 1 = TRS in Unternehmen 2
Mikroökonomik II: 14 Allgemeines Gleichgewicht
16
Effiziente Produktionsstruktur
Es ist nicht möglich, durch Umschichtung der Produktion von einem Konsumgut zu einem anderen
einen der beiden Haushalte besser zu stellen.
Die Produktionsmöglichkeitenmenge gibt an,
welche Outputkombinationen mit den vorhandenen
Inputs möglich sind. Sie wird von der oder
Transformationskurve begrenzt.
Gut 2
Trans
fo
kurve rmations-
Produktionsmöglichkeitenmenge
MRT
Gut 1
Mikroökonomik II: 14 Allgemeines Gleichgewicht
17
Die Grenzrate der Transformation MRT gibt
an, um wie viele Einheiten die von Gut 2
hergestellte Menge verändert (d.h. gesenkt)
werden muß, wenn von Gut 1 eine Einheit mehr
hergestellt werden soll.
MRT = Steigung der Transformationskurve
Bedingung für effiziente Produktionsstruktur:
MRT = MRS
Gut 2
Trans
fo
matio rnskur
ve
Effiziente Allokation
Indifferen
zkurve
Gut 1
Mikroökonomik II: 14 Allgemeines Gleichgewicht
18
Produktionsökonomie mit
Privateigentum
Eigentumsrechte und Ziele
•
Die Anfangsausstattungen an allen Gütern
(Produktionsfaktoren und Konsumgüter)
gehören den Haushalten.
•
Die Eigentumsrechte an den Unternehmen
sind zwischen den Haushalten aufgeteilt.
•
Unternehmen maximieren den Gewinn.
•
Haushalte maximieren den Nutzen.
•
Das Einkommen jedes Haushalts besteht aus
dem Wert seiner Anfangsausstattung und
den auf ihn entfallenden Anteilen an den
Unternehmensgewinnen.
Gewinnmaximierung
Ein Unternehmen produziert mit vorgegebenen
Inputs die Güter x1 und x2. Der Gewinn ist
π = p1x1 + p2x2 – Kosten .
Mikroökonomik II: 14 Allgemeines Gleichgewicht
19
Isogewinnlinien
x2 =
π + Kosten p1
− x1
p2
p2
Der gewinnmaximierende Produktionsplan wird
durch die höchste Isogewinnlinie bestimmt, die
mit der Transformationskurve noch einen Punkt
gemeinsam hat. Dort gilt MRT = p1 / p2 .
Gut 2
π + Kosten
p2
Is
og
ew
in
n
lin
ien
Gewinnmaximierender
Produktionsplan
−
p1
p2
Gut 1
Mikroökonomik II: 14 Allgemeines Gleichgewicht
20
Wettbewerbsgleichgewicht
Preise, so dass auf allen Märkten Angebot und
Nachfrage gleich sind.
Das Wettbewerbsgleichgewicht in einer
Produktionsökonomie mit Privateigentum ist
Pareto-effizient.
Gut 2
(Gewinn + Kosten) / p2
= Einkommen / p2
Effiziente Allokation
= Gleichgewicht
p1*
− *
p2
Gut 1
Mikroökonomik II: 14 Allgemeines Gleichgewicht
21
Zusammenfassung
•
Die Theorie des allgemeinen Gleichgewichts
beschreibt die simultane Preisbildung auf allen
Märkten.
•
In der Edgeworth-Box werden erreichbare
Allokationen dargestellt.
•
Die Transformationskurve begrenzt die Menge
der Outputkombinationen, die mit gegebenen
Inputs hergestellt werden können.
•
Die Grenzrate der Transformation gibt an, um
wie viele Einheiten die Produktion eines Gutes
eingeschränkt werden muss, wenn von einem
anderen Gut eine zusätzliche Einheit produziert
werden soll.
•
Pareto-effiziente Allokationen sind dadurch
gekennzeichnet, dass
- die Grenzraten der Substitution zwischen
zwei Gütern bei allen Haushalten
übereinstimmen,
Mikroökonomik II: 14 Allgemeines Gleichgewicht
22
- die Technischen Raten der Substitution
zwischen zwei Inputs bei allen Unternehmen
übereinstimmen, und
- die Grenzrate der Transformation zwischen
zwei Gütern mit der Grenzrate der Substitution
zwischen diesen Gütern übereinstimmt.
•
Im Wettbewerbsgleichgewicht passen sich die
Preise so an, dass alle Märkte geräumt sind.
•
Das Gesetz von Walras besagt, daß der Wert der
gesamtwirtschaftlichen Überschußnachfrage für
alle Preise gleich null ist.
•
Die Allokation jedes Wettbewerbsgleichgewichts
ist Pareto-effizient.
•
Jede Pareto-effiziente Allokation ist eine
Gleichgewichts-Allokation, wenn die
Anfangsausstattungen passend umverteilt
werden.
Mikroökonomik II: 14 Allgemeines Gleichgewicht
23