1 - Lösungsskizze zu Übungsblatt 13 - Hu

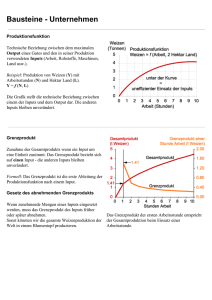
Lösungsskizze zu Übungsblatt 13
(Fehler und Irrtümer vorbehalten)
Aufgabe 1.
1. Auf dem Markt gibt es zwei Anbieter mit folgenden Angebotsfunktionen:
S1(p) = p – 10 für p≥10 und S1(p) = 0 für p < 10 sowie
S2(p) = p – 15 für p≥15 und S2(p) = 0 für p < 15
Offensichtlich gilt:
•
Ist der Marktpreis p ≥ 15, bieten beide Unternehmen an, so dass das Angebot der Branche
sich als Summe der Angebotsmengen beider Unternehmen ergibt:
S(p) = S1(p) + S2(p) = 2p – 25
•
Ist der Marktpreis 15 > p ≥ 10, bietet nur Unternehmen 1 an, so dass das Angebot der
Branche einfach der Angebotsmenge des Unternehmen 1 entspricht:
S(p) = S1(p) = p – 10
•
Ist der Marktpreis p < 10, wird keines der Unternehmen anbieten wollen, so dass das
Angebot der Branche Null ist:
S(p) = 0
Zusammenfassend gilt:
p ≥ 15
2 p − 25 wenn

S(p) =  p − 10 wenn 15 > p ≥ 10
 0
wenn
p < 10

S(p)
15
5
0
p
10
15
20
2.
(a) Wahr. Solange freier Marktaustritt möglich ist, werden die Unternehmen, die Verluste erleiden,
langfristig aus dem Markt ausscheiden.
(b) Wahr. Die langfristige Angebotskurve verläuft bei einem Preis waagerecht, der dem Minimum
der durchschnittlichen Kosten entspricht. Die Unternehmen erhalten langfristig Gewinne von Null.
Nach einer Einführung der Umsatzsteuer scheiden Unternehmen aus der Branche aus, was zu
-1-
einer Reduktion des Marktangebots und einem Anstieg des Marktpreises führt. Die Angebotskurve
verschiebt sich parallel um den Betrag der Steuer nach oben. Der Marktpreis ist gleich den
minimalen Durchschnittskosten plus Steuer.
Aufgabe 2.
(1) Jedes Unternehmen i, das auf dem Markt aktiv ist, wählt die seinen Gewinn maximierende
Angebotsmenge:
max πi(yi), wobei πî(yi) = p⋅yi – C(yi).
yi
Die Bedingung erster Ordnung des Maximierungsproblems lautet:
πî’(yi) = p – C’(yi) = 0 ⇒ p = C’(yi),
wobei C’(yi) = 2yi die Grenzkosten des Unternehmens sind. Aus der Bedingung p = C’(yi) folgt,
dass die optimale Produktionsmenge eines auf dem Markt aktiven Unternehmens durch die
Funktion
yi(p) = ½ p
beschrieben wird. Die Unternehmen stellen jedoch ihre Produktion ein, wenn sie durch die
Produktion Verluste erleiden bzw. ihre Verluste vergrössern. Es muss folglich gelten:
πi(yi(p)) = p⋅yi(p) – C(yi(p)) ≥ πi(0)
Ù
p⋅ ½ p – ( ½ p)² - 1 ≥ 0
Ù
¼ p² ≥ 1
Ù
p≥2
Die Angebotsfunktion eines Unternehmens lautet wie folgt:
1
 2 p, wenn

yi(p) = 
 0, wenn


p≥2
p<2
Sind N Unternehmen auf dem Markt aktiv, ist die kurzfristige Angebotsfunktion der Industrie gleich
1
N 1
∑ 2 p = 2 pN , wenn
N
 i =1
S
y (p) = ∑ y i ( p ) = 
i =1

0,
wenn


p≥2
.
p<2
2.) Bei der kostenlosen Möglichkeit zum Marktaustritt verlassen Unternehmen langfristig den
Markt, wenn sie Verluste erleiden. Beim freien Marktzutritt treten immer neue Unternehmen in
den Markt, solange sie positive Gewinne erwirtschaften können. Langfristig machen
Unternehmen, die auf dem Markt aktiv sind, weder Verluste noch positive Gewinne. Im
langfristigen Gleichgewicht gilt die sogenannte Nullgewinnbedingung, wobei Unternehmen die
Menge produzieren, bei der ihre Durchschnittskosten minimal sind. Sind alle Unternehmen
identisch, verläuft die langfristige inverse Angebotskurve bei einem Preis waagerecht, der gleich
dem Minimum der Durchschnittskosten eines Unternehmens ist.
min AC(yi), wobei AC(yi) =
yi
C ( yi )
1
= yi + .
yi
yi
Die Bedingung erster Ordnung des Minimierungsproblems lautet:
-2-
*
AC’(yi ) = 0 Ù 1 -
1
y i*
2
= 0,
*
woraus folgt, dass yi = 1. Jedes Unternehmen i, das auf dem Markt aktiv ist, produziert im
*
langfristigen Gleichgewicht also yi = 1.
*
3) Das Minimum der Durchschnittskosten ist gleich AC(yi ) = 2. Die langfristige inverse
Angebotsfunktion der Industrie lautet also PS(y) = 2.
4.) Die inverse Nachfragefunktion der Industrie ist durch PD(y) = 52 – y gegeben. Im langfristigen
Gleichgewicht gilt:
PS(y) = PD(y)
Ù
2
= 52 - y
y
= 50
Die im langfristigen Gleichgewicht auf dem Markt gehandelte Menge ist gleich 50. Da jedes
*
Unternehmen i, das auf dem Markt aktiv ist, im langfristigen Gleichgewicht yi = 1 produziert, sind
gerade
*
N = y / yi = 50/1 = 50
Unternehmen auf dem Markt aktiv.
Aufgabe 3.
Der Wert der Exklusivlizenz für ein Unternehmen besteht darin, langfristig positive Gewinne
erwirtschaften zu können. Denn ohne eine solche Zugangsbeschränkung würden alle auf dem
Markt aktive Unternehmen langfristig einen Gewinn von Null erhalten.
Den maximalen Gewinn von Unternehmen i=1,2 berechnet man wie folgt:
max πi(y), wobei πi(y) = p⋅y – Ci(y).
yi
Bedingung 1. Ordnung:
πi’(y) = p – Ci’(y) = 0 ⇒ p = Ci’(y),
Für Unternehmen 1 gilt:
C1’(y) = 0,002·y ⇒ p = 0,002·y Ù y = p/0,002 ⇒ y = 500 (<600 = Marktnachfrage bei p=1)
C1(500) = 0,001·500² + 100 = 350
π1(500) = 1⋅500 – C1(500) = 500 – 350 = 150
Für Unternehmen 2 gilt:
C2’(y) = 0,004·y ⇒ p = 0,004·y Ù y = p/0,004 ⇒ y = 250 (<600 = Marktnachfrage bei p=1)
C2(250) = 0,002·250² + 50 = 175
π2(250) = 1⋅250 – C1(250) = 250 – 175 = 75
Würde also das Unternehmen 1 die Exklusivlizenz erhalten, könnte es einen Gewinn in Höhe von
150 Euro erwirtschaften, während das Unternehmen 2 nur einen Gewinn von 75 erzielen würde.
Das Unternehmen 1 ist also bereit, ein höheres Gebot für die Exklusivlizenz abzugeben.
-3-