Document

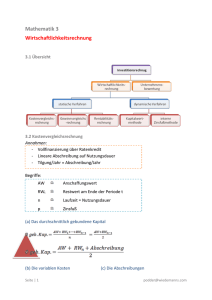
BWL III – Rechnungswesen/
Investition und Finanzierung
Ak. OR Dr. Ursel Müller
Übersicht





Methoden der Investitionsrechnung
3 klassische finanzmathematische Methoden
der Investitionsrechnung
Der Kapitalwert
Die Annuitätenmethode
Der interne Zinsfuß
2
2. Methoden der Investitionsrechnung
Zu (1) Die Kapitalwertmethode





Investitionen sind Zahlungsreihen
Typisch: Beginn mit Auszahlung und danach nur
Einzahlungen
t0
t1
t2
t3
-100
+ 50
+ 50
+ 50
Ermittlung des Barwertes für jeden beliebigen Zeitpunkt
durch Auf- oder Abzinsen!
Barwert: Gegenwartswert einer Zahlungsreihe
Kapitalwert: besonderer Gegenwartswert
3
2. Methoden der Investitionsrechnung




Kapitalwert: besonderer Gegenwartswert
Bezugszeitpunkt hier: A0 in t0
Verwendung des „richtigen“ Kalkulationszinsfußes zur
Diskontierung
Einheitszinssatz i (vollkommener und vollständiger
Kapitalmarkt)
n
Ko = ∑
t=0

Et
(1 + i)t
n
- ∑
t=0
At
(1 + i)t
Für Normalinvestitionen:
n
Et
Ko = ∑
- A0
t=0
(1 + i)t
4
2. Methoden der Investitionsrechnung

Rente: mehrere gleiche Einzahlungen, in gleichem zeitlichen
Abstand, Einzahlung jeweils am Ende der Periode
jährlich nachschüssige Rente (über n Perioden)

Der Gegenwartswert der Rente (E) über n Perioden:
K0 = E x RBWF – A0

Der Gegenwartswert einer ewigen Rente
E
K0 =
- A0
i

Ertragswert: Gegenwartswert der Netto-Einzahlungen bezogen auf
den Zeitpunkt t0
5
2. Methoden der Investitionsrechnung




a)
b)
c)
Interpretation von Kapitalwert und Ertragswert
Wahl: Durchführung der Investition oder Unterlassung
(Ja-Nein-Entscheidung)
Nein: Verzicht auf die Investition
Bedeutet:
Keine Kreditaufnahme zu i bzw.
Einsatz der Mittel in der besten alternativen Verwendung
Anlage am Kapitalmarkt zu i
Durchführung einer anderen Investition
Konsum
6
2. Methoden der Investitionsrechnung





Ökonomische Interpretation de Kapitalwertes:
Der Kapitalwert ist eine Vermögensmehrung im Zeitpunkt des
Investitionsbeginns t0
oder
derjenige Betrag, den der Investor in t0 zusätzlich konsumieren
kann (oder anlegen), wenn er z.B. einen Kredit aufnimmt zum
Zinssatz i, die Investition durchführt und mit den Einzahlungen
daraus den Kredit einschließlich der Zinsen zurückzahlt
oder
derjenige Betrag, den man maximal für die Möglichkeit, die
Investition durchzuführen, bezahlen kann, ohne sich finanziell
schlechter zu stellen als bei Verzicht auf die Investition
K0 = der Grenzpreis der Investitionsmöglichkeit
7
2. Methoden der Investitionsrechnung
Die Reinvestitions- und Finanzierungsannahmen
(1) Beschaffung von finanziellen Mitteln zum Zinssatz i
(2) Anlage der Mittel zum Zinssatz i
(3) Vollkommener Kapitalmarkt, Sicherheit, flache
Zinsstruktur, konstanter Zinssatz
(4) Vollständiger Kapitalmarkt, beliebige Teile können
angelegt und zurückgezahlt werden
(5) Einzahlungen aus dem Investitionsprojekt können
jederzeit zu i zurückgezahlt werden. Implizit notwendige
Annahme des vollst. und vollk. Kapitalmarktes. Bei
Wideranlage zu einem anderen Zinssatz ändert sich der
Kapitalwert.

8
2. Methoden der Investitionsrechnung

Das Entscheidungskriterium (auch für den MehrPerioden-Fall)

K0 ist positiv: die Investition ist vorteilhaft

K0 ist null:

die Investition ist weder vorteilhaft,
noch von Nachteil
K0 ist negativ: die Investition führt zu einer
Verringerung des Vermögens
9
2. Methoden der Investitionsrechnung
(2)





Die Annuitätenmethode
Änderung der Struktur einer Zahlungsreihe, keine Änderung des
Kapitalwertes (im vollk. Kapitalmarkt)
Annuitätenmethode
Ungleich strukturierte Zahlungsreihe 1 mit K01 wird überführt in
Eine Reihe von gleich großen Zahlungen mit gleichem Abstand
und gleichem Kapitalwert ≡ äquivalente Annuität a der
Zahlungsreihe 1
Zahlungen erfolgen nachschüssig, erster Zahlungstermin ist t1
10
Gegeben ist die Zahlungsreihe einer Investition
t0
t1
t2
t3
- 100
+ 68,18
+ 30
+ 50
11
2. Methoden der Investitionsrechnung

3 Möglichkeiten zur Ermittlung der Annuität
(1)
vom Kapitalwert her
a = K0 x WGF (n,i), a = K0 x i (ewige Rente)
(2)
Annuität der Auszahlungsreihe – Annuität der
Einzahlungsreihe
= Ø Einzahlungsüberschüsse = Gewinnannuität
(3)
vom Barwert tn
durch Multiplikation mit dem Tilgungsfaktor i / (1+i)n - 1
12
Aufzinsungsfaktor
Aufzinsung einer Zahlung
von t < tn auf tn
Abzinsungsfaktor
Abzinsung einer Zahlung
von t > t0 auf t0
Rentenendwertfaktor
(REWF)
Aufzinsung jeder Zahlung
auf tn und Addition der
Einzelwerte
Rentenbarwertfaktor
(RBWF)
Abzinsung jeder Zahlung
auf t0 und Addition der
Einzelwerte
Tilgungsfaktor
(TF)
Gleichmäßige Verteilung
des Barwertes in tn auf n
Perioden
Wiedergewinnungsfaktor
(WGF)
Gleichmäßige Verteilung
des Barwertes in t0 auf n
Perioden
13
2. Methoden der Investitionsrechnung
Interpretation

Annuität:



finanzmathematisch richtig berechnete Durchschnitt von
Zahlungen
Verteilung der Anschaffungsauszahlung und der
Nettoeinzahlungen auf die Rentendauer
Gewinnannuität: Ø Überschuss der Nettoeinzahlungen
über die auf die Nutzungsdauer der Investition verteilte
Anschaffungsauszahlung
14
2. Methoden der Investitionsrechnung
Entscheidungskriterium



Eine Investition ist vorteilhaft, wenn die Gewinnannuität
positiv ist. Von alternativen Projekten ist das mit der
höchsten Gewinnannuität zu wählen
Die Investition ist weder vorteilhaft, noch unvorteilhaft,
wenn die Gewinnannuität einen Wert von 0 hat
Eine Investition sollte nicht durchgeführt werden, wenn
die Gewinnannuität negativ ist
15
2. Methoden der Investitionsrechnung
(3)
Der interne Zinsfuß

Keine Abwandlung der Kapitalwertmethode, eigenständiges Kriterium!




Interner Zinsfuß r : Zinsfuß bei dessen Verwendung als
Kalkulationszinsfuß der Kapitalwert einer Investition Null wird
Für eine „Normalinvestition“ gilt:
n
Et
∑
- A0 = 0
t=1 (1 + r)t
Bei endlichen Renten gilt: E x RBWF – A0 = 0
E
Bei ewigen Renten gilt: r =
A0
16
2. Methoden der Investitionsrechnung
Beispiel: Eine Normalinvestition, r = 23,37
t0
t1
t2
- 100
+ 50
+ 50

1
2
3
4
t3
+ 50
5
6
Jahre
Gebundenes
Kapital am Ende
des Vorjahres
Zinsen
(2) x r
Rückflüsse
Kapitalfreisetzung
(4) – (3)
Gebundenes
Kapital am
Jahresende
1
2
3
100
73,37
40,52
23,37
17,15
9,47
50
50
50
26,63
32,85
40,52
73,37
40,52
0
∑ 213,89/3
∑ 49,99/3
= 71,30
= 16,66
16,66/71,30 = 23,37 = interner Zins
17
2. Methoden der Investitionsrechnung
Fazit:

Der interne Zinsfuß entspricht der Verzinsung des
durchschnittlich gebundenen Kapitals, nicht dagegen
der Verzinsung des eingesetzten Kapitals

Anschaffungsauszahlung durch Kredit finanziert: r = der
Sollzinsfuß, bei dessen Verwendung die Rückflüsse
gerade ausreichen, den Kredit samt Zinsen
zurückzuzahlen

r = kritischer Zinssatz; der Zinssatz bei
Fremdfinanzierung darf nicht mehr als r kosten, wenn
die Investition vorteilhaft sein soll
18
2. Methoden der Investitionsrechnung
Die Refinanzierungsannahmen
(1) Kreditrückzahlungen sind jederzeit in dem Maße
möglich, wie Einzahlungen aus dem Investitionsprojekt
vorhanden sind
(2) Einzahlungen können zum Zinssatz r angelegt werden
(Wiederanlageprämisse)
(3) Zusätzliche Mittel kosten r



Merke: Annahme (2) und (3) unterscheiden sich von der
Kapitalwertmethode und der Annuitätenmethode
Geldanlage und –aufnahme sind hier zum
Kalkulationszinsfuß möglich
19
2. Methoden der Investitionsrechnung

Entscheidungskriterium für eine Normalinvestition





r>i
r=i
r<i
KW0 > 0
KW0 = 0
KW0 < 0
Der Interne Zinsfuß allein liefert keine eindeutige
Entscheidung
Vergleich mit dem Kalkulationszinsfuß!
20
2. Methoden der Investitionsrechnung

Entscheidungskriterium für Normalfinanzierung




r < i Finanzierung ist vorteilhaft
r = i Finanzierung ist weder vorteilhaft, noch nachteilig
r > I Finanzierung sollte man unterlassen
Merke: aus Nicht-Normalinvestitionen (mehr als ein
Vorzeichenwechsel) kann man aus der Methode des
internen Zinsfußes kein eindeutiges Kriterium ableiten
21
2. Methoden der Investitionsrechnung

Die Kapitalwertfunktion (einer Normalinvestition)

Beispiel (Schulte, Wirtschaftlichkeitsrechnung, Seite 41)
t0
t1
t2
t3
t3
-1.000
+500
+400
+300
+450
K0 = - 1.000 + 500 (1+r)-1 + 400 (1+r)-2 + 300 (1+r)-3 + 450 (1+r)-3 = 0
r = 0,275
i
0
0,05
0,10
0,15
0,20
0,275
0,50
1,0
KW
650
487
349
230
128
0
-267
-556
22
2. Methoden der Investitionsrechnung
Co
650
r=0,275
i
-1000
-ao
-Co
23
2. Methoden der Investitionsrechnung

Der Zusammenhang der drei Methoden bei Ja-NeinEntscheidungen


Kapitalwertmethode und Annuitätenmethode führen
immer zu gleichen Ergebnissen, übereinstimmende
Annahme über Geldaufnahme und –anlage am
Kapitalmarkt
Kapitalwertmethode und interner Zinsfuß-Methode
führen nur bei „Normalinvestitionen“ zum gleichen
Ergebnis
24
2. Methoden der Investitionsrechnung
Auswahlentscheidungen




Regeln: mehrere sich gegenseitig ausschließende
Investitionsprojekte
Wahl des IP mit dem höchsten KW
Wahl des IP mit dem höchsten internen Zinsfuß
Bei Widersprüchen ist immer die KW-Methode
vorzuziehen
25
2. Methoden der Investitionsrechnung

a)
b)
c)
Investitions- und Finanzierungsprobleme auf einem
unvollkommenen Kapitalmarkt
Endwertmethode / vollständiger Finanzplan
Methode des Capital Budgeting (Dean-Modell)
Ermittlung endogener Grenzzinsfüße als theoretisch
richtige Lenkpreise zur optimalen Steuerung des
Investitions- und Finanzierungsverhaltens (Hering,
2008, S. 136 -142)
26
Vollständiger Finanzplan
Der Einzelunternehmer, Herr Knacks zerbricht sich den Kopf und
bittet deshalb um Ihre Mithilfe. Er hat folgende drei
Handlungsmöglichkeiten in t0:
Er hat 1.800€ übrig. Die Sparkasse bietet ihm 6 % p.a. (Festgeld
über 3 Jahre)
Realinvestition mit dreijähriger Nutzungsdauer. A0 = 2.700. Die
fehlenden 900€ würde ihm die Sparkasse als Kredit mit 10%
Zinsen p.a. einräumen bei jährlicher Tilgung von 300€. Erwartete
Zahlungsüberschüsse aus der Investition: t1: 1.170€, t2: 1.080€,
t3: 990€
Von der Betriebsgründung hat Herr Knacks noch eine
Darlehensschuld gegenüber seinem Onkel in Höhe von 1.800€.
Bei 8 % Zinsen p.a. wurde „Tilgung nach Möglichkeit“ vereinbart.
27
Aufgaben
1)
Die Alternative A (1) bezeichnet eine Finanzinvestition mit der folgenden
Zahlungsstruktur:
t1
t2
t3
A0 = -1000
+100
+100
+100
Einlösung:
+ 1.000
Alternative A (2) ist eine Realinvestition mit der
folgenden Zahlungsstruktur:
t1
t2
A0 = -1.000
PÜ = 450
PÜ = 450
a)
b)
c)
t3
PÜ = 450
Ermitteln Sie Ertrags- und Kapitalwert als Abzinsungsrechnung
Ermitteln Sie den Vermögens-Endwert und Überschuss per t3 als
Aufzinsungsrechnung
Ermitteln Sie den internen Zinsfuß
28
Aufgaben
2)
Gegeben sind folgende zwei Investitionsobjekte:
Investition 1
Zeitpunkt
t0
Auszahlung
-100
Einzahlung
Investition 2
Auszahlung
Einzahlung
t1
t2
t3
...
+ 10
+ 10
+ 10
...
- 100
+ 115,5
a)
Berechnen Sie die jeweiligen Kapitalwerte und die internen Zinssätze
bei i = 0,05 %
b)
Diskutieren Sie den Widerspruch zwischen den beiden Methoden
Lösungshinweise: Schmidt/Terberger, S. 158ff.
29
Aufgaben
3)
Der Anschaffungspreis des Investitionsprojektes M ist
48.000. die Nutzungsdauer ist 6 Jahre. Die
Einzahlungsüberschüsse betragen in den ersten drei
Jahren je 15.000, ab dem 4. Jahr je 10.000. Der
Restwert zu t = 6 wird dem Schrottwert von 2.000
entsprechen, i = 0,10.
Ermitteln Sie den Kapitalwert, die Gewinnannuität und
den internen Zinsfuß
30