Ausgleichsrechnung - Lineare Regression

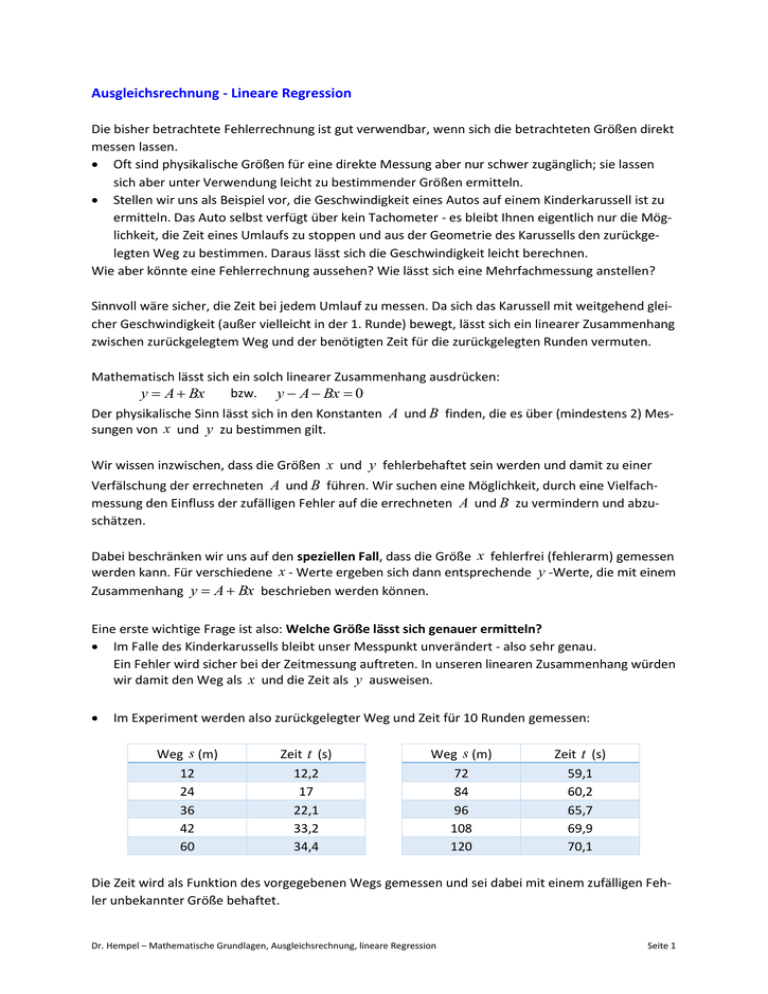
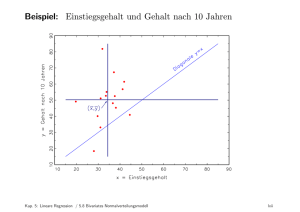
Ausgleichsrechnung - Lineare Regression
Die bisher betrachtete Fehlerrechnung ist gut verwendbar, wenn sich die betrachteten Größen direkt
messen lassen.
 Oft sind physikalische Größen für eine direkte Messung aber nur schwer zugänglich; sie lassen
sich aber unter Verwendung leicht zu bestimmender Größen ermitteln.
 Stellen wir uns als Beispiel vor, die Geschwindigkeit eines Autos auf einem Kinderkarussell ist zu
ermitteln. Das Auto selbst verfügt über kein Tachometer - es bleibt Ihnen eigentlich nur die Möglichkeit, die Zeit eines Umlaufs zu stoppen und aus der Geometrie des Karussells den zurückgelegten Weg zu bestimmen. Daraus lässt sich die Geschwindigkeit leicht berechnen.
Wie aber könnte eine Fehlerrechnung aussehen? Wie lässt sich eine Mehrfachmessung anstellen?
Sinnvoll wäre sicher, die Zeit bei jedem Umlauf zu messen. Da sich das Karussell mit weitgehend gleicher Geschwindigkeit (außer vielleicht in der 1. Runde) bewegt, lässt sich ein linearer Zusammenhang
zwischen zurückgelegtem Weg und der benötigten Zeit für die zurückgelegten Runden vermuten.
Mathematisch lässt sich ein solch linearer Zusammenhang ausdrücken:
bzw. y  A  Bx  0
y  A  Bx
Der physikalische Sinn lässt sich in den Konstanten A und B finden, die es über (mindestens 2) Messungen von x und y zu bestimmen gilt.
Wir wissen inzwischen, dass die Größen x und y fehlerbehaftet sein werden und damit zu einer
Verfälschung der errechneten A und B führen. Wir suchen eine Möglichkeit, durch eine Vielfachmessung den Einfluss der zufälligen Fehler auf die errechneten A und B zu vermindern und abzuschätzen.
Dabei beschränken wir uns auf den speziellen Fall, dass die Größe x fehlerfrei (fehlerarm) gemessen
werden kann. Für verschiedene x - Werte ergeben sich dann entsprechende y -Werte, die mit einem
Zusammenhang y  A  Bx beschrieben werden können.
Eine erste wichtige Frage ist also: Welche Größe lässt sich genauer ermitteln?
 Im Falle des Kinderkarussells bleibt unser Messpunkt unverändert - also sehr genau.
Ein Fehler wird sicher bei der Zeitmessung auftreten. In unseren linearen Zusammenhang würden
wir damit den Weg als x und die Zeit als y ausweisen.

Im Experiment werden also zurückgelegter Weg und Zeit für 10 Runden gemessen:
Weg s (m)
12
24
36
42
60
Zeit t (s)
12,2
17
22,1
33,2
34,4
Weg s (m)
72
84
96
108
120
Zeit t (s)
59,1
60,2
65,7
69,9
70,1
Die Zeit wird als Funktion des vorgegebenen Wegs gemessen und sei dabei mit einem zufälligen Fehler unbekannter Größe behaftet.
Dr. Hempel – Mathematische Grundlagen, Ausgleichsrechnung, lineare Regression
Seite 1
Der unterstellte linearen Zusammenhang t  A  Bs  0 wird nicht exakt erfüllen, d.h. für die einzelnen Zahlenpaare (sk , t k ) wird stets tk  A  Bsk  0 gelten.
Stellt man sich diesen Sachverhalt graphisch dar, liegen die gemessenen Punkte (sk , t k ) stets um
eine Differenz t k neben der Gerade t  A  Bs .

Eine fehlerfreie Berechnung der unbekannten Parameter A und B aus den Wertepaaren
(sk , t k ) wird daher nicht gelingen.

Möglich ist es, aus den Wertepaaren eine Schätzung für A und B zu gewinnen, die bei einer
wachsenden Anzahl von eingehenden Wertepaaren (sk , t k ) den wahren Zahlenwerten von A
und B beliebig nahe kommt.


Berechnet werden also B als Näherung für den wahren Parameter B und A als Näherung für
den wahren Parameter A . A und B nennt man Regressionskoeffizienten.
Welche physikalische Bedeutung haben die Koeffizienten A und B eigentlich im Beispiel?
A ist der Achsenabschnitt der Zeitachse. Er gibt uns die Zeitverzögerung beim Anfahren an.
B ist der Anstieg der Regressionsgeraden tan   t / s ; das Reziproke der Geschwindigkeit.

Die mathematische Bedingung, die der Regressionsgeraden zu Grunde liegt, lautet
10
10
k 1
k 1


 (tk )2   tk  ( B  sk  A )  min
2
A und B müssen so gewählt werden, dass die Summe aller Abweichungen (positiv und negativ daher Quadrat) minimal wird.
Die einzelnen Terme tk  ( B  sk  A ) entsprechen dabei der Differenz t k zwischen dem


Messwert t k und dem exakten Wert der Regressionsgeraden bei s k .
Dr. Hempel – Mathematische Grundlagen, Ausgleichsrechnung, lineare Regression
Seite 2

Wir berechnen die Regressionskoeffizienten A und B :
Im Minimum der Summe der quadrierten t k verschwinden die ersten partiellen Ableitungen
nach A und B .




N
2
  N
  tk  B  sk  A     2  tk  B  sk  A 
A  k 1
k 1

N
 N

 2    tk   N  A  B   sk   0
k 1
 k 1

und




N
2
  N
  t k  B  sk  A     2  t k  B  sk  A    s k 
B  k 1
 k 1
 
N
N
 N
2 
 2    sk  t k   A   sk   B   sk   0
k 1
k 1
 k 1


Wie führen Mittelwerte ein:
s
1 N
  sk
N k 1
, t
1 N
  tk
N k 1
, s2 
1 N 2
  sk
N k 1
, s t 
1 N
  sk  tk
N k 1
und erhalten damit:
N t  N  A  N  B  s  0

t  A  B s  0

s  t  A  s  B  s2  0
sowie
N  s  t  N  A  s  N  B  s2  0

Auflösen der Gleichungen nach B und A liefert die Berechnungsvorschriften
1 N
 1 N  1 N 
   sk  tk      sk      tk 
s  t  s  t  N k 1
  N k 1   N k 1 
B

2
2
s 2  s 
 1 N 2  1 N 
   sk      sk 
 N k 1   N k 1 
und
 1 N   1 N 2  1 N
 1 N 

t


s


s

t





     sk 



k
k
k
k
t  s 2  s  t  x  N k 1   N k 1   N k 1
  N k 1 
A

2
2
2
s  s 
 1 N 2  1 N 
   sk      sk 
 N k 1   N k 1 
1 N 
1 N 
A  t  B  s     tk   B     sk 
 N k 1 
 N k 1 

In unserem Beispiel bedeutet das:
s  65,4 m , t  44 ,39 s
B
s t  s t
s  s 
2
2

, s 2  4277,16 m 2
, s  t  3638,88 m  s
3638,88ms  65,4m  44,39s 735,774ms

 0,6066 s / m
5490m2  4277,16m2
1212,84m2
A  t  B  s  44,39s  1,81996 s / m  44,39m  4,7418 s
Dr. Hempel – Mathematische Grundlagen, Ausgleichsrechnung, lineare Regression
Seite 3
Physikalische Bedeutung hat hier besonders (wie oben bereits erwähnt) der Kehrwert von B ,
1
den Schätzwert für die wahre Geschwindigkeit v liefert.
B
damit wird v  (0,6066 s / m)1  1,648 m / s  5,934 km / h .
der mit der Beziehung v 


Da wir hier Fehlerrechnung betreiben, fragen wir natürlich nach dem Fehler von v !
Diesen Fehler von v gewinnen wir aus dem Fehler des Regressionskoeffizienten B .
 Also auf! Berechnen wir den Fehler von B .
1. Wir berechnen die Summe der Fehlerquadrate der Messwerte t k :

N
N
k 1
k 1

 (tk )2   tk  ( B  sk  A )  276,888 s 2
2
2. Daraus gewinnen wir die mittlere Streuung st der Messwerte t k um die Regressionsgerade:
N
2
1
  tk  A  B  sk   5,883 s
N  2 k 1
Man beachte hier das ( N  2) im Nenner !
sy 
 ( N  2) ergibt sich aus der Tatsache, dass ein Fehler im Anstieg B bzw. im
Achsenabschnitt A sinnvoll erst ab 3 Messwertepaaren bestimmt werden kann.
 welchen Anstiegsfehler könnte man z.B. bestimmen, wenn die Gerade durch genau
2 Punkte verläuft?
3. Da A und B nur mittelbar (aus den Messwerten t1 ...t10 ) errechnet werden, werden ihre
Fehler mittels Fehlerfortpflanzung ermittelt.
Es ergibt sich:
sB  s y 

1
N  s  s 
2
2

 sy 
N

 N 
2
N    sk     sk 
 k 1   k 1 
N
N
sA  sy 

s
2
N  s  s 
2
s A  sB  s 2  sB 
2

 sy 
s
k 1
2
k

 N 
2
N    sk     sk 
 k 1   k 1 
N
2
2
oder
1  N 2
   sk 
N  k 1 
Im Beispiel:
sB  s y 

1
N  s  s 
2
s A  sB  s 2  sB 
2
  0,0534 s / m
1  N 2
   sk   3,958 s
N  k 1 
Dr. Hempel – Mathematische Grundlagen, Ausgleichsrechnung, lineare Regression
Seite 4

Es bleibt spannend!
Uns interessierte eigentlich der absoluten Fehler des Schätzwertes v !
Da die Geschwindigkeit hier das Reziproke des Anstiegs, müssen wir wieder einmal die Fehlerfortpflanzung bemühen. Wie wirkt sich ein Fehler auf den Kehrwert einer Größe aus?
1
 
 v B 
 v B 
 B -1
B

Δv 
 ΔB 
 sB 
 sB 
 sB 
B
B
B
B
 
  1  B - 2  sB  

1
1
 sB  2  sB  0,145 m / s
2
B
B
Es ergibt sich somit eine Geschwindigkeit des Karussells von
v  (1,648  0,145) m / s
Ist diese Angabe sinnvoll?
NEIN !!
Wenn sich der Fehler bereits in der ersten Stelle nach dem Komma bemerkbar macht - was soll
dann eine Angabe weiterer Stellen für einen Sinn haben?
 sinnvolle Ergebnisangabe: (Fehler werden immer aufgerundet!)
v  (1,6  0,2) m / s

Aussagekräftiger als der Wert des absoluten Fehlers Δv  0,2 m / s ist häufig die Angabe des
relativen Fehlers
Δv
.
v
1
 sB durch erneutes Einsetzen des
B2
1 1
1
s
 sB    sB  v   sB  v  B
B B
B
B
ΔB

B
Dieser errechnet sich z.B., indem man die Beziehung Δv 
1
1
umformt: Δv  2
B
B
Δv s B

Division durch v ergibt dann
v
B
 die relativen Fehler von v und B sind gleich.
Zusammenhanges v 
Im Beispiel ergibt sich hier
Δv sB 0,05342
 
 0,088  8,8 %
v
B 0,60665
Der Korrelationskoeffizient r
Gelegentlich (besonders bei schwierigen Messungen) stellt sich die Frage, ob ein vermuteter linearer
Zusammenhang zwischen zwei Größen tatsächlich existiert; ob die beiden Größen also miteinander
korreliert sind.
Nicht immer sieht man es dem Diagramm der Messwerte an, wie „gut“ die eingetragenen Messwerte
auf einer Geraden liegen - oder auch nicht.
Dr. Hempel – Mathematische Grundlagen, Ausgleichsrechnung, lineare Regression
Seite 5
Quantifizieren lässt sich „gut“ hier mit dem Korrelationskoeffizienten r .
Er ist gegeben durch:
r
st  s  t
s 2  s   t 2  t 
2
2

1 N
 1 N  1 N 
   sk  tk      sk      tk 
 N k 1
  N k 1   N k 1 
2
 1 N 2  1 N 
 1 N 2  1 N 
   sk      sk      tk      tk 
 N k 1   N k 1 
 N k 1   N k 1 
2
Der Korrelationskoeffizient r kann dabei Werte zwischen r  1 und r  1 annehmen;
eine physikalische Größe lässt sich aus ihm nicht direkt gewinnen.


Je näher der Betrag von r dabei der 1 kommt, desto stärker enthalten die Wertepaare eine lineare Beziehung.
Für einen Betrag von exakt 1 liegen alle Wertepaare exakt auf einer Geraden, die für r  1 fallend und für r  1 steigend verläuft.
Für r  0 ist keine Abhängigkeit anzunehmen.

Im Beispiel ergibt sich: r   0,97035
Der Korrelationskoeffizient r   0,97035 zeigt mit dem positiven Vorzeichen eine direkte Proportionalität zwischen s und t .
Die geringfügige Abweichung zu +1 zeigt die geringfügige Abweichung der realen Messwertpaare
vom erwarteten linearen Zusammenhang.
Dr. Hempel – Mathematische Grundlagen, Ausgleichsrechnung, lineare Regression
Seite 6