EMFs

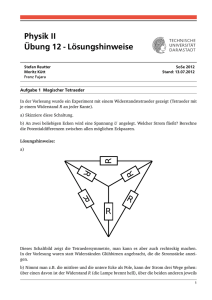
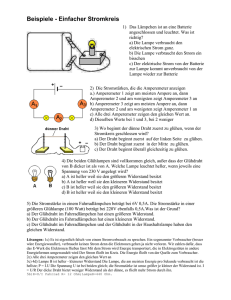
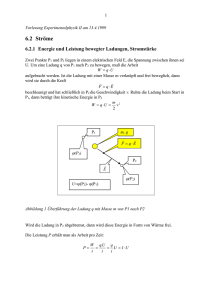
6 – Gleichstromkreis
Alle elektrischen und elektronischen Geräte enthalten Schaltkreise in der einen oder anderen Form. Wir befassen uns zunächst nur mit Gleichstromkreisen und diskutieren Wechselstromkreise später.
6.1 – Gleichstromkreis
Historisch bedingt nennt man die Potentialdifferenz, die zwischen den Polen einer Spannungsquelle besteht, die Elektromotorische Kraft EMF . Der Begriff geht auf die Verwendung von elektrochemischen Zellen (Batterien) als Spannungsquellen zurück, ist aber an sich eine Fehlbezeichnung, da sich die EMF ja nicht auf eine Kraft (Einheit: Newton) sondern eine Spannung (Einheit: Volt) bezieht. Alternativ wird auch der Begriff Urspannung verwendet.
Entnimmt man einer Batterie Ladung, d.h. lässt man über einen Verbraucher einen Strom fließen, so ist die an den Polen der Batterie messbare Spannung (Klemmspannung) kleiner als die EMF. Man denke an die Autobatterie beim Startprozess im Winter. Die Ursache dafür ist, dass die elektrochemischen Prozesse zur Aufrechterhaltung der Ladungstrennung in der Batterie nicht beliebig schnell ablaufen können. Technisch kann dieses Phänomen auf einen sogenannten Innenwiderstand Ri der Batterie abgebildet werden.
Ri

Vab
Die Klemmspannung hängt also vom Strom ab:
V ab = E −IR i
Hörsaal­Übung: An eine Batterie mit Innenwiderstand 0.5  wird ein 65  Widerstand
angeschlossen. Die Batterie hat eine EMF von 12.0 V. Welcher Strom fließt und
welche Klemmspannung stellt sich ein? Welche Leistung wird am äußeren und
inneren Widerstand umgesetzt?
6.2 – Reihen­ und Parallelschaltung von Widerständen
Die Hintereinanderschaltung von Widerständen nennt man eine Reihen­ oder Serienschaltung. Durch alle Widerstände fließt der gleiche Strom, da sich sonst ja an manchen Stellen Ladung anhäufen müsste, an anderen würde sie verarmen; das aber ist im stationären Fall nicht möglich.
R1
R2
R3
Wenn die Potentialdifferenzen über den Widerständen V1, V2 und V3 sind, so gilt:
I
V =V 1V 2 V 3=IR 1IR 2IR 3
V
Das muss so sein, denn beim Passieren eines Widerstand Ri nimmt die potentielle Energie einer Ladung um qVi ab. Die Summe dieser Absenkungen der potentiellen Energie muss qV entsprechen.
Wir können daraus unmittelbar den Wert eines äquivalenten Einzelwiderstandes R ablesen, durch den der gleiche Strom fließen würde:
V =IR  R =R 1 R 2 R 3
Bei einer Reihenschaltung addieren sich die Widerstände zum Gesamtwiderstand.
Bei einer Parallelschaltung (hier von drei Widerständen) teilt sich der Strom I, der die Batterie verlässt, auf. An jedem Widerstand fällt die Spannung V ab.
I1
R1
I2
R2
I3
R3
Wieder lässt sich der an jedem Widerstand auftretende Spannungsabfall damit plausibel machen, dass eine die Batterie verlassende Ladung q beim passieren eines der Widerstände einen gleichen Betrag an potentieller Energie verlieren muss, nämlich qV.
Aus dem Ohmschen Gesetz folgt
I 1=V / R 1 ,I 2=V / R 2 ,I 3=V / R 3
Ausserdem müssen sich die Ströme zu I addieren
I
V
I =I 1I 2I 3
Der äquivalente Einzelwiderstand R muss I = V/R erfüllen, so dass gilt
1
1
1
1
=  
R R1 R2 R3
Bei einer Parallelschaltung addieren sich die Kehrwerte der Widerstände.
Hörsaal­Übung: (Widerstandsleiter) Was ist der äquivalente Widerstand zwischen
den Abgriffen A und B für die Widerstandsleiter auf der Abbildung?
Jeder Einzelwiderstand habe den Wert 100 .
A
B
R
6.3 – Kirchhoffsche Regeln
Die Regeln für die Reihen­ und Parallelschaltung sind nicht ausreichend für die Behandlung komplexerer Schaltungen; bspw. wenn Ströme gesucht sind und eine oder mehrere Spannungsquellen berücksichtigt werden müssen.
G. R. Kirchhoff (1824­1887) hat dazu zwei Regeln formuliert, die auf die Prinzipien der Ladungs­ und Energieerhaltung zurückgehen
Kirchhoffs erste Regel lautet:
An jeder Leiterverbindungsstelle (Knoten) ist die Summe der zufließende Ströme
gleich der Summe der abfließenden Ströme.
Wegen der Ladungserhaltung gilt: was in einen Knoten hineinfließt, muss auch wieder herausfließen.
Die zweite Regel lautet:
Die Summe aller Spannungen entlang eines beliebigen, geschlossenen Teilkreises
(Masche) ist Null.
Hier hilft die Analogie mit einer Achterbahn. An einem beliebigen Punkt gestartet muss nach ihrer Rückkehr zu diesem Punkt die Summe aller Änderungen der potentiellen Energie eines Wagens gerade Null ergeben.
Wesentlich bei der Anwendung der Regeln ist, dass die Vorzeichen konsistent gewählt werden. Dazu merken wir uns:
Problemlösung – Kirchhoffsche Regeln
1. Kennzeichne die Pole aller Batterien mit + und ­.
2. Kennzeichne aller Teilströme Ik und versehe sie mit einem die Richtung
des Stromflusses andeutenden Pfeil. Diese Richtung ist frei wählbar.
3. Wende die Kirchhoffschen Regeln für einen oder mehrere Knoten und die
eine oder mehrere Maschen an. Es werden ebenso viele unabhängige Gleichungen
benötigt, wie es Unbekannte gibt. Es können auch mehr Gleichungen aufgestellt
werden, die dann aber nicht alle unabhängig sind. An jedem Widerstand kann
V=RI verwendet werden, was die Zahl der Unbekannten reduzieren kann.
4. Bei der Anwendung der Maschenregel darf jede Masche nur in einer Richtung
durchlaufen werden. Dabei gilt
(a) Für jeden Widerstand: Ist die Maschen­Durchlaufrichtung parallel zum Zweigstrom
Ik, so zählt die Spannung positiv, sonst negativ.
(b) Für jede Batterie: Ist die Maschen­Durchlaufrichtung vom negativen zum positiven
Pol, so zählt die Spannung positiv, sonst negativ.
5. Löse die Gleichungen algebraisch nach den Unbekannten.
Anwendung der Kirchhoffschen Regeln: Die Wheatstone­Brücke
Die Wheatstone­Brücke ist eine Brückenschaltung zur präzisen Bestimmung eines unbekannten Widerstandes.
I3
R3
A
R1
I1
RX ist der gesuchte Widerstand, R3 ein veränderlicher Widerstand. Dieser wird so eingestellt, dass über das Ampere­Meter kein Strom fließt. In diesem Fall liegen die Punkte B und D auf gleichem Potential. Demnach ist also VAB = VAD oder auch
RX
B
A
D
R2
D
I 3 R3= I 1 R1
V
I1 fließt dann auch durch R2 und I3 fließt auch durch RX. Die Spannungsabfälle über RX und R2 sind gleich:
I 3 R X = I 1 R2
Wir teilen die erste durch die zweite Gleichung und erhalten als Lösung
RX=
R2
R1
R3
EMFs in Serie und parallel
Werden zwei oder mehr Batterien gleichsinnig in Serie geschaltet, so addieren sich ihre Spannungen. Werden Sie hingegen gegensinnig geschaltet, so subtrahieren sich die Spannungen. Dieser Schaltungstyp wird bei Ladeschaltungen verwendet. Dabei ist der zu ladendende Akkumulator mit der Ladespannung gegensinnig in Serie geschaltet. Auch die Lichtmaschine in einem Auto lädt auf diese Art den Bleiakku auf.
Eine gleichsinnige Parallelschaltung von Batterien wird verwendet, wenn – bei gleicher Spannung – ein größerer Laststrom entnommen werden soll.
Hörsaal­Übung: (Starthilfe)
Eine gut geladene Autobatterie wird für die Starthilfe eines Wagens mit schwacher
Batterie verwendet. Diese Batterie hat eine EMF von 12,5 V und einen Innenwiderstand
von 0,02 . Die schwache Batterie hat eine EMF von 10,1 V und einen Innenwiderstand
von 0,1 . Wir nehmen an, dass der Anlasser durch einen Widerstand RS = 0,15 
repräsentiert werden kann.
(a) Welcher Strom fließt durch den Anlasser, wenn nur die schwache Batterie
angeschlossen ist?
(b) Welcher Strom fließt, wenn nun auch die gut geladene Batterie angeschlossen wird?
(c) Was würde passieren, wenn versehentlich die Polung des Starthilfekabels vertauscht
würde?
6.4 – Lade­ und Entladeverhalten eines RC­Kreises
Wir befassen uns in diesem Kapitel nun erstmals mit zeitveränderlichen Strömen. Dazu betrachten wir Schaltkreise, bei denen ein Widerstand R und ein Kondensator der Kapazität C vorkommen. RC­Kreise sind technisch von großer Bedeutung, da über sie viele zeitabhängige Funktionen gesteuert werden, Intervallschalter bspw.
Wir betrachten zunächst den folgenden einfachen Fall:
V0
­
+
C
R
S
Zum Zeitpunkt t=0 ist der Schalter S geöffnet und der Kondensator auf die Spannung V0 aufgeladen.
Was passiert, wenn der Schalter geschlossen wird? ­ Der Kondensator wird entladen und es gilt wegen der Maschenregel zu jeder Zeit
Q t 
 I t  R = 0
C
Damit lässt sich noch nicht viel anfangen, da wir zwei von t abhängige Größen Q und I in der Gleichung haben. Wir erinnern uns, dass gilt dQ/dt = I und leiten deshalb die Gleichung nach der Zeit ab, um Q zugunsten von I zu eliminieren
1 dQ
dI
=− R C dt
dt
 1
dI
I =− R
C
dt
Wir suchen die zeitabhängige Funktion I(t) für t>0. Dazu trennen wir nach den Variablen I und t
−
1
dI
dt =
RC
I
Wir integrieren links über die Zeit von 0 bis t, rechts entsprechend über den dazu korrespondierenden Strom I(t=0) = I0 und I(t)
I dI '
1 t
− ∫0 dt ' =∫I
RC
I'
0
 −
1
I t 
t = ln 

RC
I0
Durch exponentieren auf beiden Seiten können wir nach I(t) auflösen
I t = I 0 e−t / RC
Der Strom fällt also von seinem Anfangswert I0 exponentiell auf 0 ab. Die Zeitkonstante dieses Abfalls ist =RC. In der Zeit  fällt der Strom auf 37 % seines Anfangswertes.
Hörsaal­Übung: Wie lautet die Zeitabhängigkeit der Ladung Q(t) auf dem Kondensator?
6.5 – DC­Strom­ und Spannungsmessgeräte
Ströme misst man mit einem Amperemeter, Spannungen mit einem Voltmeter. Bei Zeigerinstrumenten ist der wesentlich Teil das Galvanometer. Es basiert auf der Kraftwirkung, die ein stromdurchflossener Draht in einem Magnetfeld erfährt. Dazu im nächsten Kapitel mehr. Hier genügt der Hinweis, dass die Auslenkung eines Galvanometers proportional zum Strom ist, der durch es hindurchfließt. Der Draht ist in der Form einer Spule aufgewickelt.
Mit einem Galvanometer lassen sich direkt nur kleine Ströme messen (typisch einige mA bis einige 10 µA). Zur Messung größerer Ströme wird ein Widerstand dem Galvanometer parallel geschaltet. Dieser Widerstand heisst Neudeutsch Shunt (shunt : parallel geschaltet).
IG
I
A
=
Ri
Ish
G
Der Innenwiderstand Ri eines Galvanometers ist der Widerstand des Drahtes, der die Spule bildet.
Rsh
Hörsaal­Übung: Welcher Shunt muss gewählt werden, damit bei einem Amperemeter
ein Strom von 1.0 A Vollausschlag am Galvanometer (Vollausschlag 50 µA) erzeugt?
Der Innenwiderstand sei 30 .
Ein Voltmeter besteht ebenfalls aus einem Galvanometer, dem aber ein Vorwiderstand RV in Reihe vorgeschaltet ist. Dieser Vorwiderstand ist in der Regel groß (einige 100 k bei Zeiger­Instrumenten, einige M bei Digitalvoltmetern).
V
=
RV
Ri
G
Hörsaal­Übung: Welcher Vorwiderstand muss bei einem Voltmeter gewählt werden
(Galvanometer Vollauschlag bei 50 µA, Innenwiderstand 30 ) damit es bei 15 V
Vollausschlag zeigt?
Anwendungshinweis
Amperemeter müssen in die Leitung, in der der Strom gemessen werden soll, “eingeschleift”, d.h. in Reihe geschaltet, werden. Ihr Innenwiderstand muss möglichst klein sein, um eine unverfälschte Messung zu erhalten.
Voltmeter werden zur Messung der Spannungsabfalls über zwei Kontakte (bspw. die Anschlüsse eines Widerstandes) parallel geschaltet. Ihr Innenwiderstand muss möglichst groß sein, um eine unverfälschte Messung zu erhalten.
Ein Ohmmeter besteht aus einer internen Spannungsquelle mit bekannter Spannung in Reihe mit einem Vorwiderstand und einem Amperemeter.
Ri
Rsh
G
Der zu messende Widerstand wird über die Abgriffe in Reihe geschaltet und komplettiert den Stromkreis. Die Auslenkung des Galvanometers ist umgekehrt proportional zum Widerstandswert.
Anwendungshinweis:
RV
V
Da das Ohmmeter einen Strom durch den zu messenden Widerstand fließen lässt, darf dieser nicht Teil eines Schaltkreises sein, sondern muss immer elektrisch isoliert werden. Ansonsten kann das Ohmmeter einen empfindlichen Schaltkreis zerstören.
Die Empfindlichkeit eines Messinstruments ist in der Regel auf der Frontplatte (am Galvanometer) angegeben. Dies kann in der Form /V erfolgen. Dies bedeutet den Widerstand des Instruments pro Volt anliegender Spannung bei Vollausschlag. So hat ein Voltmeter der Empfindlichkeit 30 k/V auf der 10 V Skala einen Widerstand von 300 k was nicht sehr viel ist. Für Amperemeter ist die Stromempfindlichkeit bei Vollauschlag gerade der Kehrwert der eben diskutierten Empfindlichkeit in /V.
6.6 – Transducer, Thermoelement
Unter einem Transducer versteht man einen “Energietyp­Umwandler”. Ein Lautsprecher ist bspw. ein Wandler von elektrischer Energie in Schallenergie. Umgekehrt arbeitet ein Mikrofon, das ebenfalls ein Transducer ist.
Transducer werden oftmals als Messinstrument eingesetzt. Ein wichtiges Beispiel ist das Thermoelement, das thermische Energiedifferenzen in elektrische Energie umsetzt.
V
Messpunkt
T
Metall 2
Referenz
T0
Metall 1
Das Funktionsprinzip des Thermoelements basiert auf dem thermoelektrischen Effekt: Wenn zwei unterschiedlichen Metalle (bspw. Fe und Cu) an den Enden verbunden werden (bspw. verschweisst), so wird zwischen den Enden eine Spannung beobachtet, wenn diese auf verschiedener Temperatur sind.
Dies rührt daher, dass die Elektronen in einem der Metalle eine niedrigere Energie, als im anderen Metall haben. Es kommt zu einem Elektronenfluss, der zur positiven Aufladung des einen und zur negativen Aufladung des anderen Metalls führt. Sind die beiden Kontaktstellen auf der gleichen Temperatur, stellen sich an ihnen die gleichen Kontaktpotentiale ein und es kann keine Potentialdifferenz zwischen ihnen gemessen werden. Bei Temperaturunterschied werden die Energiezustände geändert und eine Potentialdifferenz stellt sich ein (Stichwort: Austrittsarbeit).
Bei der Verwendung eines Thermoelementes wird eine der Kontaktstellen auf eine bekannte Referenztemperatur (bspw. Tripelpunkt von Wasser) gehalten. Die Thermospannung ist über einen weiten Temperaturbereich eine lineare Funktion der Temperaturdifferenz T­T0. Typische Thermospannungen sind einige µV pro Kelvin Temperaturdifferenz.
Hörsaal­Übung: Welche andere Typen von Transducern gibt es noch?