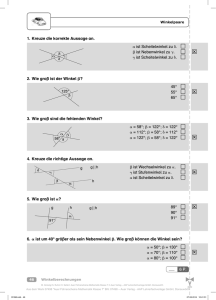
Winkel messen – Hoppelhase

Name:
Einführung
Station 8
Winkel messen – Hoppelhase
Aufgabe 1
Miss die jeweiligen Winkel und notiere die Winkelgrößen in der Tabelle.
Tipp: Wenn die Schenkel zu kurz sind, verlängere diese.
a1
Winkel
a2
a3
g1
g2
g3
d1
d2
d3
e1
e2
e3
Winkelgröße
α2
α3
α1
γ2
γ1
γ3
δ2
ε2
ε1
δ1
δ3
Aufgabe 2
Was ist denn hier geschehen?! Die Beschriftung der Winkel ist
anders als in den sonstigen Figuren. Der Fuchs hat sich drei
Winkelbezeichnungen geholt. Finde die „fehlenden“ Winkelbezeichnungen (mit tiefgestellten Zahlen) heraus und notiere sie.
Sezer Avci: Mathe an Stationen Spezial: Winkel
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
ε3
20
Aus dem Werk 07242 "Mathe an Stationen Spezial Winkel" BN: 07242 - Auer Verlag GmbH
7242.indb 20
05.11.2013 16:40:53
Name:
Winkel zeichnen und messen –
Winkelkunst
Einführung
Station 9
Aufgabe 1
Zeichne die fehlenden Schenkel der Winkel und miss danach den neuen Winkel im entstandenen
Dreieck. Arbeite genau.
Tipp: Bei b) und c) helfen dir Kreuzchen an den Streckenenden und Winkelbögen.
b)
a)
Winkelgröße:
c)
Winkelgröße:
d)
Winkelgröße:
Sezer Avci: Mathe an Stationen Spezial: Winkel
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
e)
Winkelgröße:
f)
Winkelgröße:
Winkelgröße:
Aufgabe 2
Male nun die Felder aus, die die Lösungszahlen aus Aufgabe 1 enthalten.
21
Aus dem Werk 07242 "Mathe an Stationen Spezial Winkel" BN: 07242 - Auer Verlag GmbH
7242.indb 21
05.11.2013 16:40:54
Station 3
Name:
Dreiecke – Innenwinkelsumme
entdecken
Aufgabe 1
Zeichne auf ein Blatt Papier drei unterschiedliche Dreiecke (auch unregelmäßige Dreiecke). Markiere in jedem Dreieck die Innenwinkel durch einen Winkelbogen. Färbe alle Ecken eines Dreiecks
mit einer Farbe ein und nummeriere in jedem Dreieck die Ecken (mit den Zahlen 1, 2 und 3) durch.
Schneide dann die Dreiecke aus und reiße oder schneide anschließend bei jedem Dreieck die
Ecken vorsichtig ab. Lege diese Ecken aneinander.
Aufgabe 2
Geometrische
Figuren
a) Was stellst du fest?
b) Gib, ohne zu messen, die Summe der farbigen Winkel eines Dreiecks an. Wie nennt man diese
Winkelart?
c) Formuliere mit den angegebenen Begriffen einen Merksatz zur Innenwinkelsumme in Dreiecken.
Dreieck
Grad
jedem
Sezer Avci: Mathe an Stationen Spezial: Winkel
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
einhundertachtzig
Innenwinkelsumme
38
Aus dem Werk 07242 "Mathe an Stationen Spezial Winkel" BN: 07242 - Auer Verlag GmbH
7242.indb 38
05.11.2013 16:40:59
Name:
Station 4
Dreiecke in Farbe
Aufgabe
Berechne im Kopf die Größe des jeweils fehlenden Winkel im Dreieck ABC und notiere sie in der Tabelle. Male dann im Bild die Felder mit den Lösungszahlen farbig aus.
Dreieck ABC hat die Innenwinkel:
a
b
a)
20°
80°
b)
40°
40°
100°
20°
d)
100°
e)
45°
f)
95°
50°
g)
62°
64°
h)
i)
35°
49°
99°
37°
33°
56,8°
45,5°
Sezer Avci: Mathe an Stationen Spezial: Winkel
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
j)
50°
Geometrische
Figuren
c)
g
39
Aus dem Werk 07242 "Mathe an Stationen Spezial Winkel" BN: 07242 - Auer Verlag GmbH
7242.indb 39
05.11.2013 16:40:59