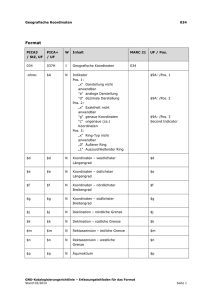
T3 - Elektrodynamik

T3 - Elektrodynamik
Ludwig-Maximilian-Universität München
Sommersemester 2014
Abschrift basierend auf den Materialien von Prof. Hofmann
Version vom 27. Juni 2014
angefertigt von: Christian Röske
Diese Abschrift ist nicht redigiert und stellt keinen Anspruch auf Vollständigkeit. Insbesondere Fehler können nicht
ausgeschlossen werden. Gerne können diese (und sonstige Anmerkungen zur Abschrift) jedoch mitgeteilt werden:
B [email protected]
Inhaltsverzeichnis
0
Relativitätsprinzipien. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
0.1 Galilei . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
0.2 Einstein . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
0.3 Minkowski . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
1
Tensoren
2
Minkowski-Raumzeit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
20
3
Heuristischer Übergang zur Klassischen Feldtheorie . . . . . . . . . . . . . . . . . . . . . . . .
25
4
Lagrange-Dichte für das elektromagnetische Potential . . . . . . . . . . . . . . . . . . . . . .
32
5
Lösungstheorie
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
5.1 Quellenfreie Theorie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
5.1.1
5.1.2
5.1.3
5.1.4
5.1.5
Die eindimensionale Wellengleichung. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
Die mehrdimensionale Wellengleichung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
Vektorwellen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
Quellenfreie elektromagnetische Wellen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
Die allgemeine Lösung der homogenen Wellengleichung . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
5.2 Absorption und Emission . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
0
Relativitätsprinzipien
3
0 Relativitätsprinzipien
Relativitätsprinzipien sind ordnende Prnzipien.
0.1 Galilei
Trägheitssatz von Galilei: In einem Inertialsystem hat ein Massenpunkt, der keinen Kräften ausgesetzt ist, eine
konstante Geschwindigkeit. Für abgeschlossene Systeme gilt das
Spezielle Relativitätsprinzip von Galilei: Die grundlegenden Gesetzte der klassischen Mechanik sind identisch in
allen Bezugssystemen, die sich mit gleichförmiger Geschwindigkeit relativ zueinander bewegen.
Dies bedeutet: Die Gesetze der Physik sind invariant unter den speziellen Galilei-Transformationen:
Gv :
R3 × R → R3 × R,
df.
(q, t) → Gv (q, t) = (q + vt, t)
für alle v ∈
R3 . Somit:
Spezielle Galilei-Transformationen sind Symmetrien physikalischer (mechanischer Systeme und führen Inertialsysteme ineinander über. Neben der Relativität der Geschwindigkeit ist auch die Richtung im Raum relativ (Isotropie).
Weiterhin sind die Festlegungen des Ursprungs im Raum und in der Zeit relativ (affiner Raum).
Dies bedeutet: Die Gesetze abgeschlossener Systeme sind auch invariant gegenüber
• Rotationen:
R:
R3 × R → R3 × R,
(q, t) → (Rq, t)
für alle R ∈ SO(3)
• Translationen:
Tw :
R3 × R → R3 × R,
df.
(q, t) → Tw (q, t) = (q + w, t)
Tδ :
R3 × R → R3 × R,
df.
(q, t) → Tδ (q, t) = (q, t + δ)
R
für alle w ∈
R
R
R3 , δ ∈ R.
R
Die Gruppe von bijektiven Abbildungen 3 ×
→ 3 × , die von den Transformationen Gv (v ∈
3
SO(3), Tw (w ∈
) und Tδ (δ ∈ ) erzeugt wird, heißt die eigentliche, orthochrone Galilei-Gruppe Γ.
R
R
R3 ), R ∈
Relativitätsprinzip von Galilei: Alle Inertialsysteme sind gleichberechtigt. Die grundlegenden Gesetze abgeschlossener Systeme sind invariant gegenüber Γ. Γ ist also eine Symmetriegruppe der Mechanik abgeschlossener
Systeme. Symmetrien erzeugen Erhaltungsgrößen. Im Falle von Γ sind es 10 Erhaltungsgrößen:
Impuls, Energie, Bahndrehimpuls, Geschwindigkeit des Massenschwerpunkts.
Γ legt eine Geometrie fest, die Galilei-Raumzeit.
Erinnerung: Eine Galilei-Raumzeit ist ein 4-dimensionaler affiner Raum M mit folgenden Eigenschaften:
1. Auf dem zu M gehörigen 4-dimensionalen Vektorraum V ist eine Linearform ∆ : V →
df.
R gegeben.
2. Auf dem Kern V0 = {v ∈ V : ∆(V ) = 0} von ∆ ist ein euklidisches Skalarprodukt gegeben, das V0 zu einem
3-dimensionalen euklidischen Vektorraum macht.
0
Relativitätsprinzipien
4
M ist dabei als Raum der Ereignisse zu interpretieren. Zu den Ereignissen a, b ∈ M ist ∆(ab) der Zeitunterschied.
df.
R
Die Fasern Vt = ∆−1 (t)(t ∈ ) beschreiben in V und damit auch in M Schichten gleicher Zeit =
ˆ räumliche Hyperebenen. Diese erhalten durch die euklidische Metrik von V0 ebenfalls eine Metrik: Für a, b ∈ M mit ∆(ab) = 0,
ist
df.
d(a, b) = |ab|
wegen ab ∈ V0 wohldefiniert. Durch diese Metrik auf Vt wird also der räumliche Abstand von Ereignissen in dieser
Zeitschicht (räumliche Hyperebene) festgelegt. Ereignissen aus unterschiedlichen Zeitschichten ist kein Abstand
zugeordnet.
Standardmodell für eine Galilei-Raumzeit:
M=
R4 als affiner Raum, V = R4 als Gruppe von Translationen
∆ : V = R3 × R → R,
df.
(q, t) → ∆(q, t) = t
d ist durch das übliche Skalarprodukt auf
übertragen.
∀(q, t) ∈ V.
R3 gegeben, und wird direkt auf V0 = R3 × {0}
Aufgabe: Skizze.
Aufgabe: Die volle Symmetriegruppe der Galilei-Raumzeit.
Soll Γ als die volle Symmetriegruppe der Galilei-Raumzeit fungieren, so ist folgende Ergänzung notwendig:
3. Die Vektorräume V, V0 sind orientiert.
Aufgabe: Zeigen Sie, dass Γ die volle Symmetriegruppe der Mechanik ist.
Kritik: Da die speziellen Galilei-Transformationen eine Gruppe bilden, gilt:
v
v
2
(q, t) →1 Gv (q, t) = (q + v1 , t) −→
(Gv2 ◦ Gv1 )(q, t)
= (q + (v1 + v2 ) t, t)
⇒ Gv2 ◦ Gv1 = Gv1 +v2
(Addition der Geschwindigkeiten)
Diese einfache Folgerung hält nun experimentellen Überprüfungen nicht stand! Insbesondere gibt es in der Natur
keine sofortigen Wirkungen (Fernwirkungen). Auf der Annahme der Existenz von Fernwirkungen beruht aber die
Mechanik nach Newton. Vielmehr beobachten wir eine Maximalgeschwindigkeit mit der sich Informationen ausbreiten. Wir bezeichnen diese Grenzgeschwindigkeit mit c. Im Rahmen der Messgenauigkeit, kann c nicht von der
Lichtgeschwindigkeit im Vakuum unterschieden werden. Die Mechanik nach Newton ist somit nicht exakt, sondern
stellt vielmehr eine sehr brauchbare Näherung dar, solange vc 1 gilt.
Aufgabe: Finden Sie in der Literatur den präzisesten Wert für die Lichtgeschwindigkeit im Vakuum, und beschreiben Sie den dazu zugehörigen Messprozess.
Damit ist auch die Galilei-Raumzeit kein exaktes Raumzeit-Modell! Es bedarf einer Erweiterung dieses Modells,
die der Existenz einer Grenzgeschwindigkeit strukturell Rechnung tragen kann.
0.2 Einstein
Aus den speziellen Galilei-Transformationen folgt ein Additionsgesetz der Geschwindigkeiten, das unverträglich mit
Beobachtungen ist. Diese Unverträglichkeit rührt von der Hypothese der absoluten Zeit, die wir offenbar aufgeben
müssen. Mit anderen Worten: Die Zeit läuft in verschieden Bezugssystemen verschieden schnell ab. Die Angabe
eines Zeitintervalls ist somit nur sinnvoll, wenn auch das Bezugssystem angegeben wird, auf das sich die Aussage
bezieht. Die Erfahrung zeigt also, dass ein allgemeineres als das Galilei’sche Relativitätsprinzip gelten muss.
0
Relativitätsprinzipien
5
Relativitätsprinzip von Einstein: Es ist unmöglich, aufgrund irgendwelcher physikalischer Erscheinungen (nicht
nur solcher der Mechanik) ein absolut ruhendes Inertialsystem zu bestimmen. Inertialsysteme sind absolut gleichwertig. Die Naturgesetze können so geschrieben werden, dass sie forminvariant (kovariant) sind gegenüber den noch
zu bestimmenden Transformationen von einem Inertialsystem in ein anderes. Die gesuchten Transformationen heißen Lorentz-Transformationen.
Herleitung der Lorentz-Transformation aus dem Relativitätsprinzip von Einstein:
Annahmen:
(A1) Der Raum ist isotrop.
(A2) Raum und Zeit sind homogen.
(A3) Alle Inertialsysteme sind gleichberechtigt.
Bemerkungen: (A1) und (A2) definieren Inertialsysteme bereits vollständig. Wegen (A2) müssen die gesuchten
Transformationen linear sein.
Aufgabe: Erläutern Sie die Bemerkungen.
Wir analysieren die folgende Situation:
y0
y
K
K0
v
0(t = 0) = 00 (t = 0)
00 (t) = (vt, 0, 0)
0
00
x
x0
linear
Für die gesuchte lineare Transformation schreiben wir

x0 = γ(v)(x − vt) 



y 0 = α(v)y
(H1)

z 0 = α(v)z



t0 = µ(v)t + ε(v)x
Bemerkungen: γ, α, µ, ε sind von den Koordinaten unabhängig, sie hängen höchstens von der Relativgeschwindigkeit v ab. Wegen der Isotropie des Raumes (A1) ist die Transformation (y, z) → (y 0 , z 0 ) alleine durch α(v) gegeben.
In der Gleichung für t0 kommen die Koordinaten (y, z) nicht vor (A1).
Aufgabe: Erläutern Sie die Bemerkungen.
Wir bestimmen nun γ, α, µ, ε
(H2): Wir transformieren x → x , x0 → −x0 , v → −v und erhalten die Orientierung. Wegen (A1) gilt:
−x0 = γ(−v)(−x + vt)
−y 0 = −α(−v)y
+z 0 = +α(−v)z
+t0 = µ(−v)t − ε(−v)x
0
Relativitätsprinzipien
6
Der Vergleich mit (H1) liefert:
γ(−v) = γ(v), α(−v) = α(v), µ(−v) = µ(v) , aber ε(−v) = −ε(v).
Statt der ungeraden Funktion ε(v) führen wir durch
ε(v) = −
v
µ(v)
η(v)
die in v gerade Funktion η(v) ein. Einsetzen liefert:

x0 = γ(v)(x − vt) 



y 0 = α(v)y
(H2)
0

z = α(v)z



v
t0 = µ(v)(t − η(v)
x)
(H3): Für die inverse Transformation notieren wir wegen (A3):

x = γ(v)(x0 − vt0 ) 



y = α(v)y 0
(H3)

z = α(v)z 0



v
x0 )
t = µ(v)(t + η(v)
(H2)
=⇒ α2 = 1 ⇒ α = ±1
Damit die Transformation für v → 0 stetig in die identische Abbildung übergeht, wählen wir
α = ±1
Jetzt rechnen wir: µ · 1. Gl. (H2) + vγ · 4. Gl. (H2) liefert
v2
x
µx0 + vγt0 = µγ 1 −
η
Auflösen nach x gibt
x=
x0
γ 1−
+
2
v
η
vt0
µ 1−
v2
η
Der Vergleich mit 1. Gleichung (H3) liefert
γ=
1
γ 1−
v2
η
, γ=
⇒ γ = µ , γ2 =
1
µ 1−
v2
η
1
2
1 − vη
Wegen unserer Forderung, dass die Transformation für v → 0 stetig in die identische Abbildung übergehen soll,
wählen wir
γ = ±q
1
1−
v2
η
Jetzt ist nur noch η unbekannt. Wir wissen bereits, dass η(v) eine gerade Funktion der Relativgeschwindigkeit v
sein muss. Wir betrachten folgende Situation:
v
v
1
2
K −→
K0 −→
K00
w
wie auf Seite 5
0
Relativitätsprinzipien
7
Aus dem Relativitätsprinzip (A3) folgt, dass die Komposition von zwei Lorentz-Transformationen ebenfalls eine
Lorentz-Transformation ist. Außerdem sind die Transformationen assoziativ und die inverse Transformation und
die identische existieren. Lorentz-Transformationen bilden somit eine Gruppe. Dazu später mehr. Es ist
x = γ(v1 ) x − v1 t
v1
0
t = γ(v1 ) t −
x
η(v1 )
0
0
x = γ(v2 ) x − v2 t
v2 00
00
0
t = γ(v2 ) t −
x
η(v2 )
0
00


v1
00

x = γ(v2 )γ(v1 ) x − v1 t − v2 t − η(v1 ) x
⇒

v1
v2
00

t = γ(v2 )γ(v1 ) t − η(v1 ) x − η(v2 ) x − v1 t
Wie oben dargelegt liefert (A3),
w
00
00
x = γ(w) x − wt , t = γ(w) t −
x
η(w)
v1 v2
v1 v 2
⇒ γ(w) = γ(v2 )γ(v1 ) 1 +
= γ(v2 )γ(v1 ) 1 +
η(v1 )
η(v2 )
⇒ η(v1 ) = η(v2 ) = const.
Die Größe η ist also eine universelle Konstante mit der Dimension einer Geschwindigkeit zum Quadrat. Die Konstante muss endlich sein: Für η → ∞ gehen die Lorentz-Transformationen in die (speziellen) Galilei-Transformationen
2
über. Diese widersprechen aber Einsteins Relativitätsprinzip und gelten lediglich approximativ für vη 1.
Wir rechnen:
v1 v2
γ(w) = γ(v2 )γ(v1 ) 1 +
η
v2
v2
(1 − η1 )(1 − η2 )
w2
=
⇒1−
η
(1 + v1ηv2 )2
⇒
1 (v1 + v2 )2
w2
=
η
η (1 + v1ηv2 )2
Vergleich der Koeffizienten von η −1 liefert:
w=
v1 + v2
1 + v1ηv2
Dies ist Einsteins Additionstheorem bei gleichgerichteten Geschwindigkeiten v1 und v2 .
df. √
Aufgabe: Zeigen Sie, dass σ = η eine Grenzgeschwindigkeit darstellt. Und: Selbst wenn ein Vorgang mit σ
im System K0 propagiert, ergibt das Additionsgesetz in einem beliebigen Inertialsystem w = σ. Nach allen experimentellen Erkenntnissen stimmt die Grenzgeschwindigkeit σ mit der Lichtgeschwindigkeit im Vakuum überein.
Aufgabe: Leiten Sie die Lorentz-Transformationen aus Einsteins Relativitätsprinzip und der Konstanz der Lichtgeschwindigkeit her.
Bei beliebiger Richtung der Relativgeschwindigkeit gehen wir so vor: Wir definieren Projektoren (mit den übli-
0
Relativitätsprinzipien
8
chen Eigenschaften)
(k)
P(~v) :
R3 → R3
(k)
df.
~x → P(~v) (~x) =
(⊥)
P(~v) :
R3 → R3
h~v , ~xi
~v ,
h~v , ~v i
df.
(⊥)
(k)
~x → P(~v) (~x) = id − P(~v) (~x)
Aufgabe: Finden Sie die Matrixdarstellung dieser Projektoren.
df.
(k)
~x(k) = P(~v) (~x) ,
0
~x(k) = γ(v) ~x(k) − ~v t ,
Mit
gilt offenbar
df.
(⊥)
~x(⊥) = P(~v) (~x)
0
~x(⊥) = ~x(⊥) ,
h~v , ~x(k) i
t0 = γ(v) t −
c2
Wir rechnen:
0
0
~x0 = ~x(k) + ~x(⊥)
= γ(v) ~x(k) − ~v t + ~x(⊥)
(k)
(⊥)
= γ(v) P(~v) (~x) − ~v t + P(~v) (~x)
(k)
(k)
= γ(v) P(~v) (~x) − ~v t + id − P(~v) (~x)
(k)
= ~x + (γ(~v ) − 1)P(~v) (~x) − γ(v)~v t)
( 0
v ,~
xi~
v
~x = ~x + (γ(v) − 1) h~h~
vt
v ,~
v i − γ(v)~
⇒
h~
v
,~
x
i
t0 = γ(v) t − c2
Dies sind die gesuchten Transformationsgleichungen.
Aufgabe: Finden Sie die mit diesen Transformationen assoziierte Matrix.
0.3 Minkowski
Uns interessiert hauptsächlich eine rationelle Formulierung der speziellen Relativitätstheorie, die auch ein mit dem
Relativitätsprinzip von Einstein verträgliches Raumzeit-Modell erlaubt. Wir denken uns Ereignisse (RaumzeitPunkte) folgendermaßen koordinatisiert:
x0 = ct , ~x = (x1 , x2 , x3 ) , x = (x0 , ~x)
Offenbar kann der Raumzeit-Punkt x zumindest lokal bezüglich einer festen Basis von
(
1 für µ = ν
df.
ν
ν
{eµ }µ∈I , I = {0, 1, 2, 3} , (eµ ) = δµ =
0 sonst
R × R3
dargestellt werden:
x = xλ eλ
(Summenkonvention!)
R
Wenigstens lokal kann die Raumzeit mit 4 identifiziert werden. Diese Identifikation muss noch mit einer mit dem
Relativitätsprinzip verträglichen geometrischen Struktur ergänzt werden. In der Galilei-Raumzeit war diese gerade
durch die Euklidische Metrik gegeben, die ja als Isometrien die vollständige Galilei-Gruppe hatte.
Das Relativitätsprinzip von Einstein impliziert insbesondere, dass ein Teilchen, welches sich in einem Bezugssystem mit c bewegt, dies auch in allen Bezugssystemen tut.
0
Relativitätsprinzipien
9
Aufgabe: Zeigen Sie dies. Diskutieren Sie die Möglichkeit, in das Ruhesystem des Teilchens zu transformieren.
Dies ist eine absolute Implikation des Relativitätsprinzips: In allen Bezugssystemen gilt:
d~x d~x
,
5 c2
dt dt
⇒ −c2 (dt)2 + dxa dxb he~a , e~b i 5 0
⇒ −c2 (dt)2 + δab dxa dxb 5 0 , a, b ∈ {1, 2, 3}
↑
Eukidische
Metrik
Wir fassen dies folgendermaßen zusammen:
df.
−(ds)2 = ηµν dxµ dxν
wobei die Minkowski-Metrik η in unseren Konventionen die folgenden Komponenten hat:


−1 0 0 0
 0 1 0 0

ηµν = 
 0 0 1 0
0 0 0 1
Bemerkung: Die Differentialgeometriker mögen mir verzeihen.
Da im gewählten Koordinatensystem η nicht vom Raumzeit-Punkt abhängt, kann die Raumzeit global mit
identifiziert werden (globale Koordinaten). Genauer:
R
Das Paar ( 4 , η) bestehend aus der differenzierbaren Mannigfaltigkeit
mit den üblichen Orientierungen) heißt Minkowski-Raumzeit,
df.
R4
R4 und der Minkowski Metrik η (zusammen
R4 , η)
M4 = (
Wegen (ds)2 5 0 (in unseren Konventionen) handelt es sich bei M4 um eine Lorentz-Mannigfaltigkeit.
Zur Interpretation von ds: Gegeben sei eine C 1 -Kurve
γ : [λ1 , λ2 ] ⊂
R → M 4,
λ → γ(λ) = xµ (λ)eµ
Dann ist das Funktional
Z γ(λ2 ) Z λ2 r
dxµ dxν
L=
=
dλ −ηµν
dλ dλ
γ(λ1 )
λ1
die Bogenlänge der Kurve γ.
Während die Angabe eines Raumzeitpunktes von Koordinatensystem abhängt, ist die Bogenlänge koordinatenunabhängig. Größen, die in allen Koordinatensystemen übereinstimmen kommen in der Physik eine besondere
Rolle zu: Sie erfüllen die notwendige Voraussetzung, um als Observable zu fungieren.
Aufgabe: Zeigen Sie, dass L koordinatenunabhängig ist. Wie sieht es mit der Minkowski-Metrik aus?
Offenbar enthält η die essentielle geometrische Information. Weiter unten untersuchen wir die Isometrien dieser
Geometrie. Zuvor jedoch: Das Quadrat der Länge eines Lorentz-Vektors x = xλ eλ ist:
df.
||x||2 = −η(x, x) = − xµ xν η(eµ , eν )
= − xµ xν ηµν
= (x0 )2 − |~x|2
0
Relativitätsprinzipien
10
(1) ||x||2 = 0 heißen lichtartig
(2) ||x||2 < 0 heißen raumartig
(3) ||x||2 > 0 heißen zeitartig
x0
x0
zeitartig
zeit artig
lichtartig
π/4
raumartig
x
x
raumartig
π/4
Aufgabe: Diskutieren Sie den skizzierten Lichtkegel. In welchen Raumzeit-Regionen bewegen sich masselose und
massive Teilchen? Ist ein raumartiges Ereignis vom Ursprung des Lichtkegels aus erreichbar? Können Ereignisse,
die in einem Bezugssystem durch einen zeitlichen Abstand voneinander getrennt sind, in einem anderen gleichzeitig
stattfinden?
Die Lorentz-Gruppe fungiert auch als Isometriegruppe, wie wir nun sehen werden: Die Lorentz-Gruppe ist
n
o
df.
O(1, 3) = A ∈ (4) : η( A x, A y) = η(x, y) ∀x, y ∈ 4
n
o
T
= A ∈ (4) : A η A = η
R
R
R
Die Koeffizienten der Matrizen aus O(1, 3) sind nicht beschränkt.
Daher ist O(1, 3) nicht kompakt. Außerdem ist
O(1, 3) nicht zusammenhängend. Für A ∈ O(1, 3) gilt det A = 1 wegen
−1 = det(η) = det
A Tη A
= det
AT
det(η) det
A
= − det
Für den Einheitsvektor e0 = (δ0λ ) gilt
2
2
2
−1 = η(e0 , e0 ) = η A 0 , A 0 = − A 00 + A 10 + A 20 +
2
2
2
2
2
⇒ A 00 = 1 + A 00 + A 10 + A 20 + A 30 = 1
A
2
A 30
2
Daher sind folgende vier Teilmengen von O(1, 3) abgeschlossen und offen in O(1, 3):
A ∈ O(1, 3) : det A = +1 und + A 00 = 1
↑ df. L− = A ∈ O(1, 3) : det A = −1 und − A 00 = 1
df. L↓+ = A ∈ O(1, 3) : det A = +1 und − A 00 5 1
df. L↓− = A ∈ O(1, 3) : det A = −1 und − A 00 5 1
df.
L↑+ =
In der Tat sind diese Mengen abgeschlossen direkt nach Definition, denn A → A 0 und det sind stetige Abbildungen. Sie sind auch offen, weil zum Beispiel L↑+ folgendermaßen beschrieben werden kann:
n
o
0
L↑+ = A ∈ O(1, 3) : det A ∈ (1/2 , 2) und A 0 > 1/2 .
0
0
Relativitätsprinzipien
11
Wieder wegen der Stetigkeit ist eine solche Menge offen. Die Lorentz-Gruppe lässt sich also zerlegen in die disjunkten
Mengen
O(1, 3) = L↑+ ∪ L↑− ∪ L↓+ ∪ L↓− ,
die alle vier zugleich abgeschlossen und offen sind. Daher ist O(1, 3) nicht zusammenhängend.
Die eigentliche, orthochrone Lorentz-Gruppe ist
n
o
0
df.
SO(1, 3) = A ∈ O(1, 3) : det A = 1 und A 0 = 1 = L↑+
SO(1, 3) ist zusammenhängend. Das liegt daran, dass sich jedes
0
df. B
R(B) =
, B ∈ SO(3)
0 1
A ∈ SO(1, 3) als Produkt von „Drehungen“
und „Boosts “(die auf Seite 5 betrachtete spezielle Lorentz-Transformationen) Lj (j ∈ {1, 2, 3}) entlang der durch
ej gegebenen räumlichen Richtung darstellen lässt. Es gilt:
A = R(B)Lj R(B 0 )
mit geeigneten B, B 0 ∈ SO(3) und j ∈ {1, 2, 3}.
Aufgabe: Zeigen Sie dies.
Weil SO(3) zusammenhängend ist, gibt es einen stetigen Weg γ in SO(3), der B mit der Einheitsmatrix verbindet. Also einen stetigen Weg R(γ)Lj (v)R(B 0 ) in SO(1, 3), der A mit Lj (v)R(B 0 ) verbindet. Und einen weiteren,
der Lj (v)R(B 0 ) mit Lj (v) in SO(1, 3) verbindet. Schließlich findet sich leicht ein stetiger Weg in SO(3), der Lj (v)
mit der Einheitsmatrix Lj (0) verbindet. Als Ergebnis finden wir die folgende Charakterisierung von SO(1, 3). SO(3)
ist die größte zusammenhängende Teilmenge von O(1, 3) welche idR4 enthält.
Außerdem sind auch die anderen Bestandteile in
n der Zerlegung
o von O(1, 3) zusammenhängend, weil sie jeweils
↑
↑
↑
diffeomorph zu L+ sind. Zum Beispiel ist L− = ηA : A ∈ L+ .
Wir halten fest: SO(3) fungiert einerseits als Gruppe von Transformationen zwischen Bezugssystemen, und andererseits als Isometriegruppe der Minkowski-Raumzeit.
Aufgabe: Ist dies ein Zufall?
1
Tensoren
12
1 Tensoren
Die folgenden Betrachtungen sind rein heuristischer Natur und entbehren jeglicher algebraischen und geometrischen
Präzision.
Sei wieder {eµ }µ∈I die kanonische Basis von M4 , also
(eµ )d = δµα
Hierbei bezeichnet α die entsprechende Komponente des Einheitsvektors eµ . Der Index µ gibt also an, welcher
Einheitsvektor betrachtet wird und bezeichnet keineswegs eine Komponente.
Anschauung: eµ liegt tangential (lokal) an der Koordinatenlinie xµ . Damit kann eµ als Ableitungsoperator
∂µ ≡ ∂x∂ µ aufgefasst werden. In der Tat gilt
eµ (xα ) = ∂µ xα = δµα
Wir haben also die Entsprechung ∂0 =
ˆ (1, 0, 0, 0)T , und so weiter. Wegen der einfachen Geometrie von M4 und
der kanonischen Koordinatenwahl, ist der lokale Charakter dieser Konstruktion nicht transparent, im allgemeinen
aber essentiell.
Die allgemeine Situation ist ganz grob die folgende: Sei M eine differenzierbare Mannigfaltigkeit, I = [t1 , t2 ] ⊂
mit 0 ∈ I, und γ eine Kurve in M, d.h.
γ:I→M
Sei (U (ϕ), ϕ) eine Koordinatenumgebung von p ∈ U (p) ⊂ M und
ϕ : U (P ) →
RdimM
ein Diffeomorphismus. Außerdem sei f : M →
R eine differenzierbare Funktion. Wir haben
M
γ
γ
U
p
I
f
R
ϕ
Rn
R
R
1
Tensoren
13
Wie ändert sich f entlang γ mit der „Zeit“? Am Punkt γ(0) = p gilt
id
z }|
{
d d −1
f
γ(t)
=
f
ϕ
ϕ(γ(t))
dt t=0
dt t=0
| {z }
Koordinatendarstellung
von γ in U(p)
Bezeichnen wir die lokalen Koordinaten mit x1 , . . . , xdimM , so ist ∀ t ∈ I mit γ(t) ∈ U (γ(0))
ϕ γ(t) = x1 (t), . . . , xdimM (t) =: x(t)
Dann gilt mit der Kettenregel
d ∂ A
f ϕ−1 (x) ,
f γ(t) = ẋ (0) A dt t=0
∂x ϕ(p)
wobei A ∈ {1, . . . , dimM}. Also,
∂ d A
f γ(t) ,
f
γ(t)
=
ẋ
(0)
A
dt t=0
∂x ϕ(p)
Wir identifizieren daher
d ∂ A
=
ˆ ẋ (0) A dt t=0
∂x ϕ(p)
In ähnlicher Art und Weise kann die gesamte Analysis über lokale Koordinatenkarten übertragen werden, sofern
diese sich hübsch zu einem Atlas kleben lassen (garantiert für differenzierbare Mannigfaltigkeiten nach Definition.)
ẋA ist die A-te Komponente des Geschwindigkeitsvektors, der im Punkt p ∈ M tangential an γ(0) anliegt, ausgedrückt durch lokale Koordinaten. ẋA ist also ein Tangentenvektor. Die Menge der Tangentenvektoren an p ∈ M (=
ˆ
allen Geschwindigkeitsvektoren aller Kurven durch p) bildet einen Vektorraum, den sogenannten Tangentialraum
Tp M an p.
Es lohnt sich auch aus buchhalterischen Gründen, die Formalismen (und die gesamt Anschauung) zu verinnerlichen. Das sehen wir schnell ein:
Sei Vp ein Tangentenvektor an p ∈ M (das heißt Vp ∈ Tp M), und U (p), ϕ eine Koordinatenumgebung von
p ∈ M. Dann gilt ja
A ∂ Vp = Vp
A
∂x ϕ(p)
Sei nun (V (p), Ψ(p)) eine weitere Koordinatenumgebung von p. Dann gilt auch
∂ Vp = VepA A ∂y Ψ(p)
wobei wir die Koordinaten mit y bezeichnet haben.
Frage: Wie hängen beide Beschreibungen zusammen?
kennen wir die Transformationsgleichungen y = f (x), so folgt aus der Kettenregel ganz einfach
B
∂ A ∂ A ∂y Vp = Vp
= Vp
∂xA ϕ(p)
∂xA ϕ(p) ∂y B Ψ(p)
A
A
B ∂y e
⇒ Vp = Vp
∂xB ϕ(p)
1
Tensoren
14
Beachten Sie, dass f nicht linear zu sein braucht. Obige Beziehung für das Transformationsverhalten von Vektorkomponenten gilt für beliebige Koordinatenwechsel (Diffeomorphismen).
Aufgabe: Können Sie die Beziehung rein algebraisch herleiten?
Aufgabe: Überzeugen Sie sich, dass diese Beziehung für Drehungen im
R3 das korrekte Resultat liefert.
Vektoren, deren Komponenten sich unter Koordinatentransformationen wie oben transformieren, heißen in der
Physik kontravariante Vektoren. Zur Kennzeichnung tragen deren Komponenten den Index immer oben.
Anschluss an die klassische Vorstellung von einem Einheitsvektor: Sei (U (p), ϕ) eine Koordinatenumgebung von
df.
p ∈ M. Die Koordinaten bezeichnen wir mit x1 , . . . , xn , n = dim M. Das ist buchhalterisch noch nicht zufriedenstellend (ohne weitere Erläuterung), schließlich müssen wir ja die Koordinaten aller Punkte in (U (p)) unterscheiden
können. Etwa so: Für jedes q ∈ U (ϕ) ist
T
ϕ(q) = x1 (q), . . . , xn (q) ∈
Rn
Also sind die Koordinaten selbst Funktionen
xj : M →
R1 ,
j ∈ {1, . . . , n}
Aufgabe: Welche Qualifikationen müssen diese erfüllen?
∂
Sei { ∂x
j }j∈{1,...,n} eine Basis in dieser Koordinatenumgebung- Diese besteht aus partiellen Ableitungen nach den
Koordinaten xj . Partielle Ableitungen wollen aber auf Funktionen wirken. Elementar ist die Wirkung auf Koordinaten:
∂ ∂ i
i
T
x
(q)
=
δ
=
ˆ
(0,
.
.
.
,
1
,
.
.
.
,
0)
=
ϕ(q)
j
↑
∂xj ϕ(q)
∂xj ϕ(q)
i=j
Ein Vektorfeld ist eine differenzierbare Zuordnung
[
V :M→
Tp M
p∈M
dass heißt jedem Punkt der Mannigfaltigkeit wird ein Vektor aus dem an diesem Punkt verankerten Tangentialraum zugeordnet. Die Qualifikation differenzierbar bezieht sich auf die Forderung, dass die Komponenten des
Vektorfeldes differenzierbar von ihrem Argument abhängen. Gilt dies in einer Basis, so in allen.
Zunächst gilt umständlich für differenzierbare Funktionen
V (p)(f ) = V (p)(f ◦ ϕ−1 ◦ ϕ)
= vϕ(p) (f ◦ ϕ−1 )
∂ j
= vϕ(p)
(f ◦ ϕ−1 )
∂ϕj ϕ(p)
in einer Koordinatenumgebung (U (q), ϕ) mit p ∈ U (q). Bezeichnen wir die Koordinaten wieder mit x1 , . . . , xn und
unterdrücken die Abhängigkeit von p in der Notation, so gilt salopp:
V (p) = V j (x)
∂
∂xj
∀p ∈ M
Achtung: Dabei haben wir die Koordinaten aller Punkte mit x1 , . . . , xn bezeichnet. Dies meint nicht, dass wir ein
globales Koordinatensystem haben!
Bemerkung: Natürlich dürfen Sie auch folgendes schreiben:
V (x) = V j (x) ej (x)
1
Tensoren
15
Wir könnten nun duale Vektoren in algebraischer Manier einführen. Oder aber wie folgt. Gegeben sei eine differenzierbare Funktion f : M →
und ein Vektor Vp ∈ Tp M. Eine interessante Frage ist, wie sich f in Richtung Vp
ändert. Die Antwort hierauf gibt das Differential von f am Punkt p ∈ M. Dabei handelt es sich um das lineare
Funktional
R
df : Tp M →
R,
df.
Vp → df (Vp ) = Vp (f )
(∗)
Diese Definition ist unabhängig von Koordinaten. In einer lokalen Koordinatenumgebung gilt den üblichen Bezeichnung
∂f
(∗)
j ∂
= Vp j j (p)
df (Vp ) = df Vp
j
∂x
∂x
Dabei meint
∂f
∂ f ◦ ϕ−1 (x)
(p)
=
j
j
∂x
∂x ϕ(p)
Aufgabe: Gelingt Ihnen eine andere Definition des Differentials?
Insbesondere könnte uns folgende Fragestellung interessieren:
∂
(∗) ∂
dxi
xi = δji
=
j
∂x
∂xj
Diese Betrachtung führt uns natürlich zum Konzept der zur Koordinatenbasis dualen Basis. Nämlich: Sei p ∈
df.
M und U (p, ϕ) eine Koordinatenumgebung. Wir bezeichnen die Koordinaten mit x1 , . . . , xn , n = dim M, und
∂
j
entsprechend die Koordinatenbasis mit { ∂xj }j∈{1,...,n} . Dann ist die hierzu duale Basis {dx }j∈{1,...,n} . Diese spannt
den sogenannten Tangentialraum Tp∗ M auf. Das allgemeinste lineare Funktional ist in diesen Koordinaten durch
∂
α=α
dxj = αj dxj
∂xj
gegeben, und heißt eine Differentialform. Beachten Sie: Nicht jede Differentialform ist das Differential einer Funktion.
Abbildungstechnisch vereinbaren wir: Eine 1-Form ist ein lineares Funktional
α : Tp M →
R
Eine differenzierbare Zuordnung einer 1-Form zu jedem p ∈ M (oder p ∈ U ⊂ M) ein kovariantes Vektorfeld. In
Koordinaten,
α = αj (x) dxj
Beispiel: df =
∂f
∂xj
dxj . Die Zahlen
R
∂f
∂f
∂x1 , . . . , ∂xn
bilden also die Komponenten eines kovarianten Vektorfeldes.
R
R
Aufgabe: Überdecken Sie 3 mit Kugelkoordinaten (r, θ, ϕ) wie üblich. gegeben sei eine Funktion f : 3 → .
Geben Sie df an. Warum macht es keinen Sinn, die Komponenten von df in diesem Koordinatensystem (und daher
in allen!) als Komponenten des Gradienten von f zu bezeichnen?
Wieder führen wir uns die buchhalterische Leichtigkeit des Formalismus vor Augen: Sei αp eine 1-Form an p ∈ M
(dass heißt αp ∈ Tp∗ M), und (U (p), ϕ) eine Koordinatenumgebung von p. Dann gilt ja
αp = αpA dxA
bei offensichtlicher Bezeichnung der Koordinaten. Sei nun (V (p), Ψ) eine weitere Koordinatenumgebung von p ∈ M.
Wir bezeichnen die Koordinaten mit y. Dann gilt auch
αp = α
epA dy A
1
Tensoren
16
Kennen wir die Transformationsgleichung y = f (x), so folgt elementar
∂f A B
A
dx
dy =
∂xB ϕ(p)
ϕ(p)
Ψ(p)
Also
αpA = α
epB
∂y B ∂xA ϕ(p)
für beliebige Koordinatenwechsel. Vektoren, deren Komponenten sich unter Koordinatentransformationen wie oben
transformieren, heißen in der Physik kovariante Vektoren. Zur Kennzeichnung tragen deren Komponenten den Index immer unten.
Erinnerung: Sei E ein n-dimensionaler Vektorraum, ausgestattet mit einem Skalarprodukt h◦, ◦i. Dann gilt für
v, w ∈ E in einer Basis {eA }A∈{1,...,n}
hv, wi = hv A eA , wB eB i = v A wB heA , eB i
Wir definieren eine Matrix g mit Komponenten
df.
gAB = heA , eB i
Damit
hv, wi = v A gAB wB
Die Matrix g heißt Metrik oder metrischer Tensor.
Aufgabe: Wann erhalten Sie die Euklidische Metrik?
Wie gewöhnlich, können wir die Metrik benutzen, um komfortabel lineare Funktionale zu konstruieren und eine Vorstellung von diesen zu entwickeln. Sei v ∈ E. Dann ist durch
df.
v ∗ (w) = hv, wi ∀w ∈ E
ein lineares Funktional definiert, v ∗ ∈ E ∗ . Mittels des Skalarproduktes (der Metrik) können wir also jedem Vektor
v ∈ E einen dualen Vektor v ∗ ∈ E ∗ zuordnen.
Sei {eA }A∈I eine beliebige Basis von E und {eB }B∈I die zugehörige duale Basis von E ∗ , so gilt
V ∗ = VB∗ eB = V ∗ (eB )eB = hv, eB ieB = hv A eA , eB ieB = v A heA , eB ieB = (v A gAB )eB
⇒ VB∗ = V A gAB
Traditionell spart man sich den ∗ und notiert salopp
VB = V A gAB
Deswegen spielt die Indexstellung zur Unterscheidung von ko- und kontravarianten Vektorkomponenten eine wichtige Rolle (Ricci).
Aufgabe: Drücken Sie wie oben nun die Komponenten eines kontravarianten Vektors durch die des zugehörigen kovarianten Vektors aus.
Aufgabe: Definieren Sie den Gradient einer Funktion als kontravarianten Vektor.
Wir kommen nun zu den zentralen Sprachelementen der gesamten Physik. Auch wenn hier die geometrische Anschauung betont wird, so handelt es sich trotzdem schlicht und einfach neue Konstruktionen, die gänzlich in der
Linearen Algebra angesiedelt sind, oder präziser: der Multilinearen Algebra.
1
Tensoren
17
Vorbereitung: Sei Tp M der Raum von Tangentialvektoren am Punkt p ∈ M einer differenzierbaren Mannigfaldf.
tigkeit mit dim M = n ∈ . I = {1, . . . , n}. Eine Basis von Tp M bezeichnen wir mit {ea }a∈I . Bezeichnen wir die
1
lokalen Koordinaten mit x , . . . , xn , so notieren wir ea = ∂x∂ a , a ∈ I. Der Zusammenhang zwischen Basisvektoren
und Derivationen ist für uns im Moment zu interessant, um das Verhalten von Tensoren unter Koordinatentransformationen zu studieren. Das weitere funktioniert aber selbstverständlich genauso, wenn Sie an der klassischen
Vorstellung eines Vektors festhalten wollen.
N
Sei Tp∗ M der zugehörige duale Vektorraum. Eine Basis von Tp∗ M bezeichnen wir mit {eA }a∈I , und ea = dxa
für a ∈ I.
Ein kovarianter Tensor vom Rang r am Punkt p ∈ M ist eine multilineare Abbildung
T ∗ : Tp M × ... × Tp M →
|
{z
}
R
r Faktoren
Multilinear meint hierbei, dass die Funktion T ∗ (v1 , . . . , vr ), v1 , . . . , vr ∈ Tp M, linear in jedem Argument ist, vorausgesetzt, dass alle anderen Argumente festgehalten werden.
Beispiele: Ein kovarianter Vektor ist ein kovarianter Tensor vom Rang 1. Ein kovarianter Tensor 2. Stufe (=
ˆ
Rang 2) heißt auch eine bilineare Abbildung (von Vektoren). Der bekannteste kovariante Tensor 2. Stufe ist wohl
die Metrik. In Koordinaten gilt:
T ∗ (V1 , . . . , Vr ) = T ∗ (V1a1 ea1 , . . . , Vrar ear )
= V1a1 T ∗ (ea1 , . . . , Vrar ear )
= V1a1 ...Vrar T ∗ (ea1 , . . . , ear )
wobei aj ∈ I für j ∈ {1, . . . , r}. Dies notieren wir auch so:
T ∗ (V1 , . . . , Vr ) = Ta∗1 ...ar V1a1 ...Vrar
df.
mit der Setzung Ta∗1 ,...,ar = T ∗ (ea1 , . . . , ear ).
a
Unter einem Basiswechsel eeb = ∂x b ea ∀a, b ∈ I transformieren sich die Komponenten eines kovarianten Tensors
∂e
x
vom Rang r wie folgt:
Tea∗1 ...ar = T ∗ (e
ea1 , . . . , eear )
=
∂xb1
∂xbr ∗
·
·
·
T (eb1 , . . . , ebr )
a
∂e
x 1
∂e
xar
Wegen der Multilinearität der Abbildung.
Zum merken:
∂xb1
∂xbr ∗
Tea∗1 ···ar =
·
·
·
T
∂e
xa1
∂e
xar b1 ···br
Aufgabe: Wie transformiert sich die Euklidische Metrik beim Übergang von kartesischen zu sphärischen Polarkoordinaten? Wie ihre Komponenten?
Die Menge aller kovarianten Tensoren vom Rang r ist ein Vektorraum (unter den üblichen Operationen). Die
Addition wird hierbei komponentenweise erklärt, ebenso die Multiplikation mit reellen Zahlen.
Aufgabe: Wie viele Komponenten hat ein kovarianter Tensor vom Rang r?
Der Vektorraum aller kovarianten Tensoren vom Rang r bezeichnen wir mit
Tp∗ M ⊗ · · · ⊗ Tp∗ M ≡
|
{z
}
r Faktoren
r
O
Tp∗ M
1
Tensoren
18
Sind α und β kovariante Vektoren, α, β ∈ Tp∗ M, so können wir aus ihnen leicht einen kovarianten Tensor 2. Stufe
bilden, das sogenannte Tensorprodukt von α und β. Dafür erklären wir
α ⊗ β : Tp M × Tp M →
R
df.
(v, w) → α ⊗ β(v, w) = α(v)β(w)
In Koordinaten,
α ⊗ β(ea , eb ) = α(ea )β(eb ) = αa βb
Nach einer Vorbemerkung kommen wir alsbald zu kontravarianten Tensoren. Zunächst erinnern wir uns, dass
kontravariante Vektoren als Derivationen auf Funktionen wirken. Dies macht die Dualität zwischen kontra- und
kovarianten Vektoren nicht sehr transparent. Um diese manifester zu machen, bemerken wir:
Ein kontravarianter Vektor v ∈ Tp M kann als lineare Funktion aufgefasst werden:
v : Tp∗ M →
R
df.
α → v(α) = α(v)
Aufgabe: Zeigen Sie, dass v(α) linear ist.
Ein kontravarianter Tensor T vom Rang s ist eine multilineare Abbildung
T : Tp∗ M × · · · × Tp∗ M →
{z
}
|
R
s Faktoren
Ähnlich wie zuvor ist
T (α1 , . . . , αs ) = T (α1a1 ea1 , . . . , αsas eas ) = α1a1 T (ea1 , . . . , asas eas ) = ... =
= α1a1 · · · αsas T (ea1 , . . . , eas )
Wir setzen
df.
T a1 ···as = T (ea1 , . . . , eas )
und notieren
T (α1 , . . . , αs ) = α1a1 · · · αsas T a1 ···as
e
xa b
∀a, b ∈ I transformieren sich die Komponenten eines kontravarianten Tensors
Unter einem Basiswechsel eea = ∂∂x
b e
der Stufe s wie folgt
Tea1 ···as = T (e
ea1 , . . . , eeas )
∂e
xa1
∂e
xas
=
· · · bs T (eb1 , · · · , ebs )
b
1
∂x
∂x
∂e
xas b1 ···bs
∂e
xa1
·
·
·
T
=
b
∂x 1
∂xbs
Zum merken:
∂e
xas b1 ···bs
∂e
xa1
·
·
·
T
Tea1 ···as =
b
∂x 1
∂xbs
Aufgabe: Nennen Sie Beispiele für kontravariante Tensoren. Zeigen Sie, dass die zu g inverse Metrik g −1 ein kontravarianter Tensor 2. Stufe ist.
Die Menge aller kontravarianten Tensoren der Stufe s ist auch ein Vektorraum (übliche Qualifikation, komponentenweise realisiert). Diesen bezeichnen wir mit
Tp M ⊗ · · · ⊗ Tp M ≡
|
{z
}
s Faktoren
s
O
Tp M
1
Tensoren
19
Ähnlich wie oben erklären wir für v, w ∈ Tp M:
v ⊗ w : T ∗ M × Tp∗ M →
R
df.
(α, β) → v ⊗ w(α, β) = v(α)w(β)
Ein gemischter Tensor, r mal kovariant und s mal kontravariant, ist eine multilineare Abbildung T mit
T : Tp M × · · · × Tp M × Tp∗ M × · · · × Tp∗ M →
{z
} |
|
{z
}
r Faktoren
R
s Faktoren
Mit den üblichen Bezeichnungen gilt
T (v1 , . . . , vr , α1 , . . . , as ) = α1a1 · · · αsas T a1 ···as b1 ···br V1b1 · · · Vrbr
Aufgabe: Zeigen Sie dies.
Aufgabe: Zeigen Sie: unter einem Basiswechsel transformieren sich die Komponenten eines gemischten Tensors
wie folgt:
∂e
xc 1
∂e
xcs ∂xb1
∂xbr a1 ···as
Tec1 ···cs d1 ···dr =
·
·
·
·
·
·
T
b1 ···br
∂xa1
∂xcs ∂e
xd1
∂e
xdr
Aufgabe: Nennen Sie Beispiele für gemischte Tensoren. Zeigen Sie, dass die lineare Abbildung A : Tp M → Tp M
einen gemischten Tensor 2. Stufe induziert.
df.
Sei v ∈ Tp M, α ∈ Tp∗ M. Das Tensorprodukt v ⊗ α ist der durch (v ⊗ α)(β, w) = β(v)α(w) definierte gemischte
Tensor gemeint.
Aufgabe: In Anlehnung unseres Vorgehens beim Übergang von der punktweisen Konstruktion von Vektoren zu
Vektorfeldern, erklären Sie das Konzept eines gemischten Tensorfeldes.
Bemerkung: Sei A ein kovariantes Vektorfeld. In Komponenten bezüglich einer lokalen Basis, A = Aα dxα . Wir
fragen nun, ob ∂α Aβ in dieser Basis die Komponenten eines kovarianten Tensors 2. Stufe sein können? Hierbei
df.
haben wir die populäre Abkürzung ∂α = ∂x∂α verwendet.
Zur Beantwortung dieser Frage untersuchen wir das Verhalten von ∂α Aβ unter beliebigen Koordinatentransformationen x = f (e
x). Zunächst ist
∂f α (e
x) β
de
x
∂e
xβ
∂f λ (e
x)
eβ (e
⇒A
x) = Aλ (f (e
x))
∂e
xβ
A(x) = Aα (x)dxα = Aα (f (x))
Lassen Sie uns nicht zu eilig sein und das Kalkül entschlacken:
λ
∂x
eβ (e
A
x) = Aλ (x) β
∂e
x
eλ (e
⇒ Aβ (x) = A
x)
∂e
xλ
∂xβ
Jetzt ist es ökonomisch sinnvoll!
2
Minkowski-Raumzeit
20
2 Minkowski-Raumzeit
R
Wir hatten das Paar ( 4 , η) Minkowski-Raumzeit M4 genannt. M4 ist die einfachste Vakuumlösung der Allgemeinen Relativitätstheorie. In natürlichen Koordinaten, siehe 0.3,
−(ds)2 = ηµν dxµ ⊗ dxν
= −dx0 ⊗ dx0 + δab dxa ⊗ dxb
Diese Koordinaten heißen natürlich, weil Geodäten von folgender Form sind:
γ:I⊂
R → M4
df.
λ → γ(λ), xα (λ) = ϕα (γ(λ)) = λU α + C α
α
wobei U α,C Konstanten sind.
Nun beschreiben Geodäten Bahnen von Teilchen, die sich frei bewegen. In obigen Koordinaten bewegen sich frei
Teilchen also auf Geraden. Sie bieten sich daher als natürliche Koordinaten an, mit denen wir Inertialsysteme
überdecken.
Außerdem reicht eine einzige solchen Koordinatenumgebung für ganz M4 . Da zwei beliebige Raumzeit-Punkte
von M4 eindeutig durch eine Geodäte verbunden werden können, heißt M4 auch geodätisch vollständig.
Eine in die Zukunft gerichtete zeitartige Kurve ist eine differenzierbare Kurve
γ:I⊂
R → M4
λ → γ(λ), −η(γ̇(λ), γ̇(λ)) ≡ ||γ̇(λ)||2 > 0
∀λ ∈ I
Mit C + (p) bezeichnen wir die chronologische Zukunft von p ∈ M4 . Dabei handelt es sich um die folgende Menge
von Raumzeit-Punkten (Ereignisse):
df. C + (p) = q ∈ M4 ∃ γ : I → M4 , γ(0) = p , γ(1) = q und − η(γ̇(λ), γ̇(λ)) > 0 ∀λ ∈ I
Man kann zeigen, dass C + (p) ist immer eine offene Teilmenge von M4 . Im Allgemeinen ist p 6∈ C + (p).
Aufgabe: Kann p ∈ C + (p) gelten in M4 ?
Für jede Teilmenge S ⊂ M4 definieren wir
[
df.
I + (S) =
I + (p)
p∈S
I + ist offen in M4 .
Aufgabe: Definieren Sie die chronologische Vergangenheit von p ∈ M4 .
In M4 ist I + (p) exakt die Menge von Raumzeit-Punkten, die von p ∈ M4 aus mit einer in die Zukunft ge0
richteten zeitartigen Geodäte erreicht werden können. Der Rand von I + (p) (oder die Hülle), I + (p) notiert, wird
von den lichtartigen Geodäten generiert, die von p ∈ M4 aus starten.
Bemerkung: Für andere Raumzeiten gelten diese Aussagen im allgemeinen nicht, lokal jedoch immer. Dies zeigt
die besondere Bedeutung von M4 für die lokale Analyse von Raumzeiten.
Eine Teilmenge S ⊂ M4 heißt achronal, wenn
@ p, q ∈ S : q ∈ C + (p)
0
0
Tatsächlich ist C + (S) für jede Teilmenge S ⊂ M4 achronal. Das sehen wir so: Sei q ∈ C + (S), und p ∈ C + (q). Dann
0
ist q ∈ C − (p). Da C − (p) offen in M4 ist, gibt es eine offene Umgebung U (q) von q mit U (q) ⊂ C − (p). Da q ∈ C + (S)
2
Minkowski-Raumzeit
21
nach Voraussetzung, folgt U (q) ∩ C + (S) 6= ∅. Also, P ∈ C + (U (q) ∩ C + (S)) ⊂ C + (S) → C + (q) ⊂ C + (S).
0
Ähnlich zeigen wir, dass C − (q) = M4 \C + (q). Wir nehmen jetzt an, dass C + (S) nicht achronal ist und führen
0
0
diese Annahme zum Widerspruch. Wäre C + (S) nicht achronal, dann gäbe es q, r ∈ C + (S) mit r ∈ C + (q), und somit
auch r ∈ C + (S). Nun ist C + (S) aber offen, daher gilt
0
C + (S) ∩ C + = ∅
0
Folglich muss C + (S) achronal sein.
Aufgabe: Fertigen Sie eine aussagekräftige Skizze an.
Aufgabe: Geben Sie explizite Beispiele (auch nicht-triviale) für achronale Teilmengen in Zusammenhang mit
dem Lichtkegel an.
Achronale Teilmengen von M4 spielen eine wichtige Rolle, um Anfangswertprobleme global zu analysieren. Zuvor
ist allerdings eine Ausweitung unserer Kurven-Botanik notwendig. Nämlich:
Eine in die Zukunft gerichtete kausale Kurve Λ ist eine differenzierbare Kurve
γ : I ⊂ → M4 , λ → γ(λ) , −η Λ̇(λ), Λ̇(λ) = 0
∀λ ∈ I
R
Die kausale Zukunft K+ (p) von p ∈ M4 ist definiert als die folgende Teilmenge von Ereignissen:
df. K+ (p) = q ∈ M4 ∃ γ : I → M4 , γ(0) = p , γ(1) = q , −η (γ̇(λ), γ̇(λ)) = 0
∀λ ∈ I)
Es gilt also immer p ∈ K+ (p). In M4 ist K+ (p) eine abgeschlossene Teilmenge. Ähnlich wie zuvor setzen wir
[
K+ (S) =
K+ (p)
p∈S
für eine Teilmenge S ⊂ M4 . Analog definieren wir die kausale Vergangenheit eines Raumzeit-Punktes und einer
Teilmenge.
Aufgabe: Zeigen Sie: Ist q ∈ K+ (p)\C + (p), dann ist jede q und p verbindende kausale Kurve lichtartig.
Sei γ(λ) eine in die Zukunft gerichtete kausale Kurve. p ∈ M4 heißt zukünftiger Endpunkt von γ, wenn es zu
jeder Umgebung U (p) ein λ0 ∈ I gibt mit γ(t) ∈ U (p) ∀t0 < t ∈ I. Wir denken uns M4 immer so topologisiert,
dass das Trennungsaxiom von Hausdorff gilt. Daher hat γ höchstens eine zukünftigen Endpunkt. Dieser braucht
allerdings nicht auf der Kurve zu liegen. Die Kurve γ(λ) heißt unausweitbar in die Zukunft, wenn sie keinen zukünftigen Endpunkt besitzt. Unausweitbarkeit in die Vergangenheit wird analog erklärt.
Bisher lag unser Augenmerk auf Teilmengen von Ereignissen, C + (S) oder K+ (S), die von einer vorgegeben Teilmenge S von Ereignissen beeinflusst werden konnten. Jetzt werden wir mutiger und fragen nah Ereignissen, die
gänzlich durch S bestimmt sind. Im Falle von M4 sind sogar alle Ereignisse durch ein entsprechend gewähltes S
bestimmt, wie wir unten sehen werden.
Sei S eine abgeschlossene, achronale Teilmenge von M4 . Der zukünftige Einflussbereich D+ (S) von S ist
df.
D+ (S) = {p ∈ M4 in die Vergangenheit unausweitbare kausale Kurve durch p schneidet S}
Offenbar gilt immer S ⊂ D+ (S) ⊂ K+ (S). Da S als achronal angenommen wird, ist außerdem D+ (S) ∩ C − (S) = ∅
Aufgabe: Interpretieren Sie D+ (S) informationstechnisch.
D+ (S) ist von großem Interesse, denn bei geeignet vorgegebenen Anfangsbedingungen auf S, erlaubt die kausale Struktur Vorhersagen für Ereignisse in D+ (S) zu machen.
2
Minkowski-Raumzeit
22
Umgekehrt, ist p ∈ C + (S) aber p 6∈ D+ (S) ...
Aufgabe: Vervollständigen Sie den Satz.
Der vergangene Einflussbereich D− (S) von S ist
df.
D− (S) = {p ∈ M4 Jede in die Zukunft unausweitbare kausale Kurve durch p schneidet S}
Der totale Einflussbereich von S ist definiert als
df.
D(S) = D+ (S) ∪ D− (S)
D(S) ist die vollständige Menge von Ereignissen, die durch Kenntnis gewisser Daten auf S vollständig bestimmt
sind.
Eine abgeschlossene, achronale Teilmenge Σ ⊂ M4 mit
D(Σ) = M4
0
heißt eine Cauchy-Fläche. Jede Cauchy-Fläche ist eine eingebettete C-Untermannigfaltigkeit von M4 . Dies rechtfertigt unsere Sprechweise. Da Σ nach Voraussetzung achronal ist, können wir und Σ als im ganzen Raum fixierten
Zeitpunkt vorstellen. Tatsächlich sind die Flächen
x0 = const. ∀p ∈ M4
eine Familie von Cauchy-Flächen, die ganz M4 überdecken. Da M4 eine Cauchy-Folge besitzt, ist M4 eine sogenannte global-hyperbolische Raumzeit. Dies meint, dass die gesamte Zukunft und Vergangenheit eines physikalischen Systems aus der Kenntnis gewisser Bedingungen zum durch Σ repräsentierten Zeitpunkt bestimmt werden
kann.
Aufgabe: Was passiert in Raumzeiten, die keine Cauchy-Fläche haben? Ist dies physikalisch sinnvoll?
Bemerkung: In natürlichen Koordinaten (Vergleiche Seite 20) bleibt das raumzeitliche Volumenelement unter
Lorentz-Transformation erhalten,
d4 x = d4 x
e
Wir werden dies später geometrisieren. Es findet hier Erwähnung, weil wir als bald invariante Ausdrücke in Vektorfeldern konstruieren werden, wobei die Invarianz sich lediglich auf Lorentz-Transformationen von Inertialsytemen
in natürlichen Koordinaten bezieht. Wir hätten ja auch Kugelkoordinaten einführen können. In der üblichen Notationen ist dann
−(ds)2 = −dx0 ⊗ dx0 + dr ⊗ dr + r2 (dθ ⊗ dθ + sin2 (θ)dϕ ⊗ dϕ)
Aufgabe: Zeigen Sie dies. Wie sieht das entsprechende raumzeitliche Volumenelement aus?
Aufgabe: Wie viele Koordinatenumgebungen brauchen Sie mindestens, um ganz M4 zu überdecken?
Erinnerung: Wir fanden früher:
Die Lorentz-Gruppe ist:
df. O(1, 3) = Λ ∈
= Λ∈
R(4) η(Λx, Λy) = η(x, y)
R(4) ΛT η Λ = η
∀x, y ∈ M4
Die eigentliche, orthochrone Lorentzgruppe ist
SO(1, 3) = Λ ∈ O(1, 3) detΛ = 1 und Λ00 = 1
2
Minkowski-Raumzeit
23
Elemente dieser Gruppe haben bezüglich der natürlichen Basis die Komponenten


γ
−βx γ
−βy γ
−βz γ
2
(γ−1)β
(γ−1)βx βy
(γ−1)βx βz 
 −β
1 + β2 x


x
β2
β2
µ


2
Λν =
(γ−1)βy
(γ−1)βy βz 
(γ−1)βx βy
1
+
2
2
2
−βy γ

β
β
β
(γ−1)βz2
(γ−1)βy βz
(γ−1)βx βz
−βz γ
1 + β2
β2
β2
~ βi
~
mit β~ = ~v /c und β 2 = hβ,
Aufgabe: Zeigen Sie, dass dies mit unserem früheren Ergebnis auf Seite 8 übereinstimmt.
Wir kommen nun zu der auf Seite 19 angedeuteten Einschränkung. Zunächst überdecken wir M4 global mit
natürlichen Koordinaten. Dies repräsentiert ein Inertialsystem (Laborsystem).
Mittels Λ(v) ∈ SO(1, 3) transformieren wir in ein anderes Inertialsystem. Die beiden Koordinatensysteme stehen folgendermaßen zueinander in Beziehung: x
e = Λ(v) · x.
Wir spezialisieren jetzt:
Ein kovariantes Lorentz-Tensorfeld vom Rang r ist eine multilineare Abbildung
T : M4 × · · · × M4 →
R
In Koordinaten,
T (V1 (x), . . . , Vr (x)) = V1 µ1 (x) · · · Vr µr (x)Tµ1 ···µr (x)
wobei
Teµ1 ···µr (e
x) = (Λ−1 (v))ν1 µ1 · · · (Λ−1 (v))νr µr Tν1 ···νr (x)
mit x = Λ−1 (v) · x
e
Ein Lorentz-Tensor braucht kein Tensor zu sein, da die Spezialisierung Diff(M4 ) → SO(1, 3) als Transformationsgruppe eine vehemente Einschränkung bedeutet und insbesondere nichtlineare Transformationen ausschließt.
Zum Beispiel können die δα Aβ (Vergleiche Seite 19) Komponenten eines kovarianten Lorentz-Tensors 2. Stufe
sein. Wir wissen aber bereits, dass sie nicht die Komponenten eines Tensors sein können.
Ein kontravariantes Lorentz-Tensorfeld vom Rang s ist eine multilineare Abbildung
T : M4∗ · · · M4∗ →
R
In Koordinaten,
T (α1 (x), . . . , αs (x) = α1µ1 (x) · · · αsµs (x)T µ1 ···µs (x),
wobei
Teµ1 ···µs (e
x) = Λ(v)µ1 ν1 · · · Λ(v)µs νs T ν1 ···νs (x)
Bemerkung: Wir haben ja eine Metrik. Daher
df.
linear
αµ = η(∂µ , ◦) : M4 −→
R
ein kovariantes Lorentz-Vektorfeld, und zwar
df.
α0 = −dx0 , αa = dxa für a ∈ {1, 2, 3}.
2
Minkowski-Raumzeit
24
Umgekehrt, sei
df.
η −1 = η αβ ∂α ⊗ ∂β , η −1 = diag(−1, 1, 1, 1).
Dann ist
df.
linear
V µ = η −1 (dxµ , ◦) : M4∗ −→
R
ein kontravariantes Lorentz-Vektorfeld, und zwar
V 0 = −∂0 , V a = ∂a für a ∈ {1, 2, 3}.
Dies lässt sich geradeaus multilinear verallgemeinern. Die Metrik erlaubt so einen bequemen Wechsel zwischen
kovarianten und kontravarianten Lorentz-Tensorfeldern.
Aufgabe: Referat zum Ricci-Kalkül.
Ein r-fach kovariantes und s-fach kontravariantes Lorentz-Tensorfeld ist eine multilineare Abbildung
T : M4 × · · · × M4 × M4∗ × · · · × M4∗ →
{z
} |
{z
}
|
r
R
s
In Koordinaten,
T (V1 (x), . . . , Vr (x), α1 (x), . . . , αs (x)) = V1 µ1 (x) · · · Vr µr (x)α1ν1 (x) . . . αsνs (x)T ν1 ···νs µ1 ···µr (x)
wobei
Teµ1 ···µs ν1 ···νr (e
x) = Λµ1 α1 · · · Λµs αs T α1 ···αs β1 ···βr (Λ−1 )β1 ν1 · · · (Λ−1 )βr νr
mit x = Λ−1 · x
e
3
Heuristischer Übergang zur Klassischen Feldtheorie
25
3 Heuristischer Übergang zur Klassischen
Feldtheorie
Wir betrachten ein System aus N gleichen Punktmassen m, die durch Federn gleicher Federkonstanten k verbunden
sind, sodass der Konfigurationsraum 1 ist:
R
m
k
m
k
m
a
Der Abstand zweier Punktmassen betrage in der Ruhelage a. Uns interessiert die Dynamik dieses Systems um die
Ruhelage, also die Gleichgewichtslage, ohne diese zu destabilisieren. Die kinetische Energie des Gesamtsystems ist
N
T =
1X
mΦ̇2j
2 j=1
wobei Φj = f (t) die Auslenkung der j-ten Punktmasse aus ihrer Gleichgewichtslage zum Zeitpunkt t bezeichne.
Die potentielle Energie ist
N
V =
1X
k(Φj+1 − Φj )2
2 j=1
Damit finden wir für die Lagrange-Funktion dieses Systems
N
L=
1 X
mΦ̇2j − mω 2 (Φj+1 − Φj )2
2 j=1
Wir normieren die Auslenkungen auf den Abstand zweier Punktmassen in der Ruhelage und notieren
(
2 ) X
N
N
1X
m 2 m 2 2 Φj+1 − Φj
L=
a
aLj
Φ̇j − ω a
=
2 j=1
a
a
a
j=1
Tatsächlich liefert dies die gleichen Bewegungsgleichungen wie
(
2 )
N
1X
Φj+1 − Φj
2
2 2
L=
a Φ̇j − a ω
2 j=1
a
Der Ausdruck für die potentielle Energie ist gewissermaßen nicht-lokal, da die Auslenkung der (j + 1)-ten Punktmasse mit der Auslenkung der j-ten Punktmasse relativ zum Abstand beider in der Ruhelage verglichen wird.
Im Grenzfall a → 0 (und N → ∞) geht der diskrete Index j in einen kontinuierlichen über. Die Bedeutung
dieses kontinuierlichen Index ist offenbar die Postion (der Ort) an dem die Auslenkung abgefragt wird.
Die Zeit, ebenso ein kontinuierlicher Index, haben wir als Argument von Φ notiert, und genauso wollen wir die
Ortsabhängigkeit notieren:
Φj (t) → Φ(t, x)
Damit ist im Grenzfall a → 0, N → ∞ die dynamische Variable ein Feld geworden. Zeit und Ort parametrisieren
dies lediglich, nun aber wenigstens gleichberechtigt. In diesem Rahmen ist
Φj+1 − Φj
Φ(t, x + a) − Φ(t, x)
∂
→
→
Φ(t, x)
a
a
∂x
3
Heuristischer Übergang zur Klassischen Feldtheorie
26
df.
Die Größe Ve = aω geht in diesem Grenzfall gegen eine Konstante v, die die Dimension einer Geschwindigkeit trägt,
m
[v] =
s
Riemann folgend finden wir
Z
1 2
1
2
2
L(t) =
(∂t Φ) (t, x) − v (∂x Φ) (t, x)
dx
2
2
R
Der Integrand
df.
L(Φ̇, Φ0 , t, x) =
1
1 2
Φ̇ (t, x) − v 2 Φ02 (t, x)
2
2
heißt die Lagrange-Dichte des betrachteten Systems. Die Wirkung ist jetzt ein Funktional der Felder:
Z tf
Z tf Z
S[Φ] =
L=
dxL(Φ̇, Φ0 , t, x)
ti
R
ti
Das Prinzip von Hamilton auf diese Verallgemeinerung übertragen, fordert, dass die Wirkung (das Wirkungsfunktional) für physikalische Prozesse, die das System im Zustand zum Zeitpunkt ti in den Zustand zum Zeitpunkt
tf überführen, stationär sei. Hieraus folgen die Bewegungsgleichungen als Euler-Lagrange-Gleichungen für das
Variationsproblem (mehr zur Mathematik unten).
∀x ∈
δS[Φ] = 0 δΦ(ti , x) = 0 , δΦ(tf , x) = 0
R
Die Herleitung der Euler-Lagrange-Gleichung verläuft analog zur Klassischen Mechanik. Grob,
Z tf Z
δS[Φ]
!
δΦ(t, x) = 0
δS[Φ] =
dt
dx
ti
R δΦ(t, x)
δS[Φ] !
⇒
= 0 , t ∈ [tf , ti ]
δΦ(t, x)
R
df.
Wir setzen I = [tf , ti ] ⊂ und rechnen für a ∈ {t, x}
Z
Z
δ
1
e
dt
de
x (∂a Φ)2 (e
t, x
e)
δΦ(t, x) I
2
Z
Z Rh
i
=
de
t
de
x ∂a δ (1) (t − e
t)δ (1) (x − x
e) ∂a Φ(e
t, x
e)
ZI ZR
= − de
t
de
x δ (1) (t − e
t) δ (1) (x − x
e) ∂a2 Φ(e
t, x
e)
R
=
I
−(∂a2 Φ)(t, x)
Aufgabe: Qualifizieren Sie dies mathematisch.
Als Bewegungsgleichung erhalten wir somit
2
2
∂
2 ∂
−v
Φ(t, x) = 0,
∂t2
∂x2
also eine homogene, lineare partielle Differentialgleichung zweiter Ordnung, die noch um die Anfangsdaten ergänzt
werden muss, damit das Problem vollständig formuliert ist. Die allgemeine Lösung dieser Gleichung ist von folgender
Form:
Φ(t, x) = f (−) (z − ) + f (+) (z + )
df.
wobei z s = x + s · vt, s ∈ {−, +}, und f (s) zweimal stetig differenzierbar sei in (t, x). Ansonsten werden die
Funktion f (s) nicht weiter eingeschränkt. Die Anfangsdaten seinen
(
(+)
Φ(ti , x) = f (−)
n (x − vti ) + f (x + vti )
o
(−)
Φ̇(ti , x) = v − ∂f
∂z − (x − vt) +
∂f (+)
∂z + (x
+ vti )
3
Heuristischer Übergang zur Klassischen Feldtheorie
27
In der Tat gilt
df (s)
∂ (s) s
∂z s df (s)
=
sv
f (z ) =
∂t
∂t dz s
dz s
2
∂
∂ df (s)
d2 f (s)
∂ 2 (s) s
d2 f (s)
⇒ 2 f (s) (z s ) = sv
= s2 v 2
,
f (z ) =
2
s
2
s
∂t
∂t dz
∂x
dz
dz s2
Da s2 = ±1, folgt
2
2
∂
2 ∂
−v
f (s) (z s ) = 0
∂t2
∂x2
Über Eindeutigkeit etc. werden wir später nachdenken.
Aufgabe: Verallgemeinern Sie unsere heuristischen Betrachtungen auf drei räumliche Dimensionen.
Wir bleiben zunächst noch bei einer räumlichen Dimension. Uns interessiert jetzt das folgende Anfangswertproblem:
Für v > 0 geben wir als Daten zum Zeitpunkt ti
Φ(ti , x) = δ (ti , x0 )
Φ̇(ti , x) = γ (ti , x0 )
df.
vor, wobei δ und γ den kompakten Träger I = [x0 − , x0 + ] ( > 0) haben. Anschaulich handelt es sich um
bei x0 ∈ lokalisierte Funktionen. Außerdem sei für x ∈ I das Feld Φ von der Form Φ(ti , x) = f (x − vti ).
R
Zum Zeitpunkt t > ti ist Φ dann um x0 + v(t − ti ) > x0 lokalisiert. Interpretieren wir Φ(ti , x) als anfängliches Signal (Information mit kompaktem Träger), so propagiert dieses mit fortschreitender Zeit nach rechts. Die
maximale Geschwindigkeit dieser Informationsausbreitung ist offenbar durch den Parameter v bestimmt. Damit ist
die Interpretation von v geklärt. Eine kausale Analyse folgt später.
Aufgabe: Zeichnung und Beispiele für Φ(ti , x).
In Übereinstimmung mit Einsteins Relativitätsprinzip interessiert uns vor allem der Fall v = c, dass heißt die
maximale Ausbreitungsgeschwindigkeit von Informationen ist durch die in der Speziellen Relativitätstheorie gegebene Grenzgeschwindigkeit gesetzt. Diese ist bei heutiger Präzision, nicht von der Lichtgeschwindigkeit im Vakuum
zu unterscheiden.
In M4 ist die von uns betrachtete Lagrange-Dichte einfach
1 2
Φ̇ (t, ~x) − c2 δab (∂ a Φ∂ b Φ)(t, ~x)
2
1 2
= c (−η00 )(∂ 0 Φ∂ 0 Φ)(x) − c2 ηab (∂ a Φ∂ b Φ)(x)
2
−c2
=
ηµν (∂ µ Φ∂ ν Φ)(x)
2
L0 (∂µ Φ, x) =
Diese Lagrange-Dichte liefert die selbe Bewegungsgleichung wie
1
L(∂µ Φ, x) = − ∂λ Φ(x)∂ λ Φ(x)
2
Die Euler-Lagrange-Gleichung ist
df.
Φ(x) = 0 (+ Anfangsbedingungen), = ηαβ ∂ α ∂ β
Aufgabe: Zeigen Sie dies.
Bemerkung: Die maximal mögliche Ausbreitungsgeschwindigkeit ist im -Operator implementiert, unabhängig
3
Heuristischer Übergang zur Klassischen Feldtheorie
28
davon ob sich das Feld (beziehungsweise Beobachtungsgrößen) tatsächlich mit dieser Geschwindigkeit ausbreiten.
Damit prägt der -Operator den entsprechenden physikalischen Prozessen gewissermaßen die durch den lokalen
Lichtkegel induzierte kausale Struktur auf. Dies ist sinnvoll, da L(∂µ Φ, x) offenbar ein freies Feld beschreibt, genauer dessen kinetische Energiedichte. Wechselwirkungsfreie Systeme unterliegen aber immer kausalen Anforderungen
und daher sind diese immer in dem Operator implementiert, der die freie Evolution des Systems beschreibt.
Aufgabe: Erläutern Sie die Bemerkung so quantitativ wie möglich.
Aufgabe: Referat zu sogenannten Massen- beziehungsweise Energie-Dimension.
Bemerkung:
Sei c = 1 und ~ = 1 Bezeichne
E=
ˆ Energieeinheit, T =
ˆ Zeiteinheit, L =
ˆ Längeneinheit
und [ ] die durch [E] = E, [T ] = E −1 , [L] = E −1 [T α Lβ ] = [T ]α [L]β für α, β ∈
R
charakterisierte Vorschrift. Dann gilt einerseits
[L] =
E
= E4
[L]3
und andererseits
[L] = [∂Φ]2 =
[Φ]2
= E 2 [Φ]2 ⇒ [Φ] = E
L2
Damit können wir nun allgemeinere Theorien skalarer Felder konstruieren. Zunächst eine Erinnerung:
Sei B ein Inertialsystem, ausgestattet mit einem kanonischen Koordinatensystem Σ, und Be ein Beobachter, der
sich relativ zu B gleichförmig mit der Geschwindigkeit v bewegt.
e ausgestattet. Sei p ∈ M4 ein Raumzeit-Punkt mit KoordinaBe sei ebenfalls mit kanonischen Koordinaten (Σ)
ten
e µ ∈ {0, 1, 2, 3}
xµ (p) ∈ Σ, x
eµ (p) ∈ Σ,
Dann gibt es eine Lorentz-Transformation
df.
e x → L(v)(x) = x
L(v) : Σ → Σ,
e
Genauer,
df.
x(p) → L(v) (x(p)) = x
e(p)
Ein Lorentz-Skalarfeld
Φ : M4 →
R
transformiert sich trivial unter Lorentz-Transformationen, dass heißt
e x) = Φ(x)
Φ(e
Es ist üblich p ∈ M4 zu unterdrücken. Genauer haben wir
e (e
Φ
x(p)) = Φ (x(p))
Mit Hilfe der entsprechenden inversen Lorentz-Transformation finden wir
e = Φ ◦ L−1 (v).
e (e
Φ
x(p)) = Φ L−1 (v)(e
x(p)) ⇒ Φ
3
Heuristischer Übergang zur Klassischen Feldtheorie
29
e im allgemeinen nicht dieselbe Form wie Φ als Funktion von x! Die oft verwendete abkürAls Funktion von x
e hat Φ
e darf nicht zu Missverständnissen führen. Wir verallgemeinern jetzt unsere Konstruktion
zende Schreibweise Φ = Φ
(in Hinblick auf die Elektrodynamik, es geht noch allgemeiner): Bisher hatten wir
1
L(0) (∂Φ, x) = − ∂λ Φ(x)∂ λ Φ(x)
2
betrachtet. Dieser Term transformiert sich wie ein Lorentz-Skalarfeld, denn
1
L(0) (∂Φ, x) = − η(dΦ(x), dΦ(x))
2
Wir wollen das expliziter einsehen und rechnen ganz überausführlich:
1
g
(0) (∂Φ,
f x
e x), dΦ(e
e x))
L
e) = − η (dΦ(e
:::::::::
2
1
e x) ∂eβ Φ(e
e x)
= − ηe (de
xα , de
xβ ) ∂eα Φ(e
2
1
e x) ∂eβ (e
x)
= − ηeαβ ∂eα Φ(e
2
1
= − ηeαβ ∂eα Φ(L−1 (v) · x
e) ∂eβ Φ(L−1 (v) · x
e)
2
1
η αβ ∂µ Φ(x) ∂v Φ(x)
= − (L−1 )µα (v)(L−1 )νβ (v)e
2
1
= − η µν ∂µ Φ(x) ∂v Φ(x)
2
1
= − η (dΦ(x), dΦ(x)) = L(0) (∂Φ, x)
:::::::::
2
In der Tat transformiert sich die die L(0)agrange-Dichte wie ein Lorentz-Skalarfeld.
Aufgabe: Konsequenz für die Bewegungsgleichungen?
Wie stark schränkt nun die Forderung nach Lorentz-Kovarianz die Konstruktion der freien Skalarfeld-Theorie
ein?
Zunächst scheint doch auch
0
L(0) (∂Φ, x) = c0 Φ(x) Φ(x)
ein legitimer Ausdruck zu sein.
0
Aufgabe: Leiten Sie die Euler-Lagrange-Gleichung für L(0) her.
Auch ohne die Bewegungsgleichungen herzuleiten, können wir uns folgendermaßen ein Urteil erlauben:
Z
Z
4
(0)0
d x L (∂Φ, x) =
d4 x L(0) (∂Φ, x) + R[Φ]
M4
M4
!
wobei der Randterm (c0 = 12 )
Z
df. 1
R[Φ] =
d4 x ∂ρ {Φ(x)∂ ρ Φ(x)}
2 M4
In der Abwesenheit von Rändern fordern wir stets, dass R[Φ] = 0 gilt.
Aufgabe: Interpretieren Sie diese Forderung. Warum ist sie gerechtfertigt?
Aufgabe: Konstruieren Sie die allgemeinste Lagrange-Dichte, in der jeder Term aus zwei Ableitungen und zwei
Feldern besteht, sich Lorentz-kovariant transformiert und Masse-Dimension vier hat.
3
Heuristischer Übergang zur Klassischen Feldtheorie
30
Auch wenn es vom Standpunkt unserer heuristischen Überlegungen her unverständlich erscheint, so ließe zumindest
Lorentz-Kovarianz der Lagrange-Dichte auch folgende Terme zu:
N, c[4−4p] ∈ R
wobei [c[4−4p] ] = E 4−4p . p ∈ N garantiert einen polynomialen Beitrag. Dies bedeutete aber die Einführung einer
c[4−4p] η p (dΦ, dΦ) , p ∈
kompensierenden Energieskala (für p > 1), deren physikalische Bedeutung hier nicht gewürdigt werden kann,
jedenfalls nicht in Gänze. Folgendes kann uns an dieser Stelle aber inspirieren: Sei Λ diese Energieskala, also
c
c[4−4p] = 4(p−1) , c ∈
Λ
Der Einfachheit halber betrachten wir lediglich ein Monom mit p > 1. Im Moment noch etwas lax interpretieren
wir
1
ε(0) = η(dΦ, dΦ)
2
als kinetische Energiedichte. Wir betrachten
R
L = ε(0) + c[4−4p] η p (dΦ, dΦ)
(p > 1)
c
= ε(0) + 4(p−1) η p (dΦ, dΦ)
Λ
p
2p c
1
(0)
= ε + 4(p−1)
η(dΦ, dΦ)
2
Λ
p
2
c
= ε(0) + 4(p−1) {ε(0) }p
(Λ
(0) p−1 )
ε
(0)
p
=ε
1+2 c
Λ4
Wir verstehen: Λ ist die energetische Grenze zwischen zwei Regimen. Für kinetische Energien ε(0) Λ4 finden
wir dass L ≈ L(0) gilt. In diesem Regime haben wir den heuristischen Übergang zur klassischen freien Feldtheorie
vollzogen und besitzen daher bereits einige Anschauung. Diese Anschauung verlangt von uns, das Monom als eine
Art der Selbstwechselwirkung von Φ zu interpretieren. Im betrachteten Regime ist Φ also nahezu frei und „spürt
sich selbst kaum.“
Für kinetische Energien ε(0) Λ4 dagegen dominiert diese Selbstwechselwirkung gegenüber der freien Dynamik.
Das System besteht hauptsächlich aus potentieller Energie. Offenbar unterscheidet Λ also zwei grundverschiedene Regime, die physikalisch absolut entgegen gesetzten Situationen entsprechen. Daher muss die Skala Λ selbst
irgendwie physikalisch konstituiert werden, muss eine physikalische Ursache haben. Für die in dieser Vorlesung
betrachteten Effekte kann immer ε(0) Λ4 angenommen werden, also p = 1 und dieser Beitrag ist ja bereits in
ε(0) enthalten.
Welche Wechselwirkungsterme können wir notieren, die sich Lorentz-kovariant transformieren, keine Ableitungen
enthalten und Massendimension vier haben? Hier ein Vorschlag:
L(1) (Φ, x) =c[0] Φ4 (x) + c[1] Φ3 (x) + c[2] Φ2 (x) + c[3] Φ1 (x)
c[j] ∈
R,
j ∈ {0, 1, 2, 3}
Wir setzen zunächst c[3] = 0 und rechtfertigen dies a posteriori. Dann ist
L(1) (Φ, x) =
2
X
c[j] Φ4−j (x)
j=0
Die Parameter c[1] , c[2] tragen eine positive Massendimension. Diese stellen keine Probleme dar, denn
L(Φ, x) = L(0) (Φ, x) + L(1) (Φ, x)


2


4−j
X
c[j]
Φ (x)
= ε(0) (Φ, x) 1 +
j/4
(4−j)/4
(0)
(0)


{ε (Φ, x)} {ε (Φ, x)}
j=0
3
Heuristischer Übergang zur Klassischen Feldtheorie
31
Hier ist es also möglich, ε(0) beliebige Skala zu haben und erwartungsgemäß eine näherungsweise freie Theorie
vorzufinden, dass heißt L ≈ L(0) .
Der Koeffizient c[2] heißt die dem Feld Φ zugeordnete Masse.
Aufgabe: Warum hat c[2] diese Interpretation? Tipp: Relativistische Energie-Impuls-Beziehung.
Wir widmen uns nun dem Term c[3] Φ. Zunächst: Hätten wir das diskrete System von Seite 25 nach der Anfangsauslenkung nicht einfach sich selbst überlassen (frei), sondern einer externen Kraft (Antrieb) unterworfen, so
hätte sich dies durch einen Beitrag fj (t)Φj (t) in der Lagrange-Funktion bemerkbar gemacht. In der Mechanik von
Punktteilchen darf diese externe Kraft fj (t) nicht explizit vom Ort abhängen, da der Ort ja ein dynamischer Freiheitsgrad ist. Hier wird dagegen fj (t) von außen vorgegeben und die Rückwirkung des Systems auf die Krafterzeugung als vernachlässigbar angenommen. Daher wird die externe Kraft nicht in dynamische Freiheitsgrade aufgelöst.
Die externe Kraft kann Auslenkungen aus der Ruhelage selbst erzeugen oder diesen entgegenwirken. Beim heuristischen Übergang zu einer Feldtheorie entspricht der externen Kraft eine Quelldichte ρ(x), die sowohl als Quelle
als auch als Senke des Feldes fungiert, dieses also „emittieren und absorbieren“ kann. Diese Quelldichte bleibt eine
externe Größe, an die das Feld zwar koppelt, jedoch ohne eine Rückwirkung zu erzeugen. Eine solche Rückwirkung
kann berücksichtigt werden, erfordert aber selbst eine dynamische Theorie für die die Quelldichte konstituierenden
Freiheitsgraden.
Der Betrag c[3] Φ(x) kann nun in ρ(x)Φ(x) absorbiert werden und findet prinzipiell so Berücksichtigung. Es hat
sich eingebürgert, die quadratischen Terme (in den Feldern) der freien Theorie zuzurechnen, höhere Potenzen von
Φ als Selbstwechselwirkung zu bezeichnen und den Term linear in Φ als Ankopplung an eine externe Quelle zu
interpretieren. Wir finden so:
1
1
L(Φ, x) = − η(dΦ(x), dΦ(x)) − m2 Φ2 (x) + c[1] Φ3 (x) + c[0] Φ4 (x) + ρ(x)φ(x)
2
2
Aufgabe: Formulieren Sie einen präzisen Regelkatalog, der die Gestalt dieser Lagrange-Dichte erzwingt. Diskretisieren Sie Terme der Form c[−n] Φ4+n (n ∈ \ {0}), c[4+n] Φ−n , etc.
N
Aufgabe: Gegeben sei
1
L(Φ, x) = − η(dΦ(x), dΦ(x)) + ρ(x)Φ(x)
2
Diskutieren Sie, ob eine raumzeitliche homogene Quelle konsistent ist.
Bemerkung: Die Integrationstheorie der zugehörigen Bewegungsgleichungen verschieben wir auf später. Sie folgt
sobald wir eingesehen haben, in wie weit diese etwas mit Elektrodynamik zu tun haben.
Bemerkung: Folgende Schreibweise ist üblich:
L(Φ, dΦ, x) = ...
4
Lagrange-Dichte für das elektromagnetische Potential
32
4 Lagrange-Dichte für das elektromagnetische
Potential
Aus Beobachtungen folgt, dass die mit elektromagnetischen Phänomenen verknüpfte Zustandsbeschreibung auf
sogenannten Feldstärke-Vektoren beruht.
Da wir eine manifest Lorentz-kovariante Beschreibung anstreben, konstruieren wir die zugehörige Lagrange-Dichte
aus Lorentz-Vektorfeldern und deren Ableitungen. Diese Beschreibung fallt etwas üppig aus: Im Vakuum tragen die
Feldstärke-Vektoren lediglich zwei Freiheitsgrade, während unsere Beschreibung vier-komponentige Objekte nutzt.
Für eine Lorentz-kovariante Beschreibung zahlen wir also den Preis, redundante Komponenten in die Zustandscharakterisierung einbezogen zu haben. In dieser Redundanz kann keine Physik abgelegt werden, sie ist absolut
unphysikalisch und wir dürfen uns ihrer bequem aber sinnvoll entledigen.
Wir versuchen zunächst diese Aussagen etwas präziser zu würdigen. Hierbei hilft eine fundamentale Erfahrung,
welche besagt:
Es gibt keine Quellen oder Senken für elektrische Ladungen.
Betrachten wir einen Raumbereich B, so gilt für die elektrische Ladung QB in diesem Bereich folgende Bilanzgleichung:
Q̇B + I(B) = 0
wobei I(B) den Strom von elektrischen Ladungen durch die Oberfläche (B) von B bezeichne. Da auf der rechten
Seite dieser Gleichung weder eine Erzeugungsrate noch eine Vernichtungsrate auftritt, liefert diese spezielle Bilanzgleichung einen wichtigen Satz über die Erhaltung der elektrischen Ladung.
Aufgabe: Interpretieren Sie den Erhaltungssatz.
In Anlehnung an unsere Betrachtungen auf Seite 31, formulieren wir den Erhaltungssatz mittels Dichten. Sei ρ
die Ladungsdichte der Gesamtladung QB im Raumbereich B und ~j die zu I(B) gehörende Stromdichte. In der
Sprache der klassischen Vektoranalysis:
Z
~ , ~ji
I(B) =
hdF
(B)
Mit dem Satz von Gauß finden wir für den Erhaltungssatz
Z
Z
d
dV ρ +
dV div~j = 0
dt B
B
Bei zeitunabhängigem Integrationsbereich B folgt daraus die sogenannte Kontinuitätsgleichung,
∂ρ(t, ~x)
+ div~j(t, ~x) = 0
∂t
was gerade die differentielle Form der Ladungserhaltung ausdrückt. Dieser Sachverhalt lässt sich leicht kovariantisieren: Sei J(x) das kontravariante Vektorfeld mit Komponenten
J µ (x) = (ρ(x), ~j(x))
Dann gilt
∂λ J λ (x) = 0
Da die Lorentz-Stromdichte J nicht von Freiheitsgraden abhängt, kann sie als externe Quelle für die LorentzVektorfelder A(x) dienen, die wir zur (redundanten) Beschreibung von elektromagnetischen Phänomenen benutzen.
Die Lorentz-Stromdichte (zusammengesetzt aus einer Ladungsdichte und einer räumlichen Stromdichte) kann das
4
Lagrange-Dichte für das elektromagnetische Potential
33
kovariante Vektorfeld A(x) aufnehmen (absorbieren) oder abgeben (emittieren). In der Sprache der Klassischen
Elektrodynamik können Ladungs- und räumliche Stromdichten als Quellen und Senken für A(x) fungieren. Diese
Kopplung modellieren wir analog zu unseren Betrachtungen auf Seite 31 durch folgenden Term (minimale Ankopplung) in der Lagrange-Dichte:
Lext = Aλ (x)J λ (x)
Bemerkung: [J] = E 3 ⇒ [A] = E 1
Lext transformiert sich offenbar wie ein Lorentz-Skalarfeld. Ladungserhaltung hat nun eine wichtige Konsequenz:
(k)
df.
Felder der Form Aλ (x) = ∂λ f (x) (f eine Funktion) entkoppeln von der externen Quelle, können also weder
emittiert noch absorbiert werden. Wir sehen das so:
Z
(k)
d4 xAλ (x)J λ (x) = 0
M4
Vom Standpunkt der Quelle her sind also zwei kovariante Vektorfelder A1 (x) und A2 (x) äquivalent, wenn sie sich
lediglich um den Lorentz-Gradienten einer Funktion f (x) unterscheiden:
A1 (x) ∼ A2 (x) , wenn A1 (x) − A2 (x) = df (x)
Buchhalterisch haben wir es zunächst also immer mit einer Äquivalenzklasse zu tun:
e:A
e = A + df für f : M4 →
[A] = {A
R}
Der Raum der kovarianten Vektorfelder zerfällt so und uns interessiert der entsprechende Quotientenraum.
Diese Wahlfreiheit ist Ausdruck der anfangs erwähnten Redundanz. Die externe Quelle koppelt aufgrund der Ladungserhaltung an Äquivalenzklassen von kovarianten Vektorfeldern. Die Quelle diskriminiert lediglich zwischen
Repräsentanten, nicht aber innerhalb einer Äquivalenzklasse.
Nun sind für die Physik natürlich nur die Vektorfelder interessant, die auch absorbiert werden können, dass heißt
die an einem Detektor koppeln und so prinzipiell beobachtet werden können (über die von ihnen induzierten Phänomene). Es ist hierbei wichtig zu beachten, dass die Kopplung
(k)
Aλ (x) J λ (x)
im allgemeinen nicht verschwindet, aber diese sogenannte Vertexdichte ist eben auch kein Lorentz-Skalar! Daher
wird in der Wirkung über ganz M4 integriert, also
Z
df.
Sext [A] =
d4 x Aλ (x)J λ (x)
M4
Dies macht auch physikalisch Sinn: Wir „summieren“ über alle Quellenereignisse in der Raumzeit. Wir wissen bereits, dass Sext [A(k) ] = 0.
Da in diesem Sinne A(k) weder emittiert noch absorbiert wird, wollen wir diesen Feldern auch keine kinetische
Energie erlauben: Nur die Feldkonfigurationen sollen sich in der Raumzeit ausbreiten, die auch an Quellen koppeln
können. Dies schränkt die Konstruktion der „freien“ Wirkung wesentlich ein!
Prinzipiell kommen für die freie Wirkung folgende Terme in Frage:
Z
Sfrei [A] =
d4 x e
c1 ∂µ Aν ∂ µ Aν + e
c2 ∂µ Aµ ∂ν Aν + e
c3 Aλ Aλ + e
c4 Aµ ∂ µ ∂ ν Aν (x)
M4
mit e
ci ∈
R
für i ∈ {1, 2, 3, 4}
Aufgabe: Erläutern Sie das Konstruktionsprinzip.
4
Lagrange-Dichte für das elektromagnetische Potential
34
Mittels partieller Integration finden wir
Z
Sfrei [A] =
d4 x {c1 ∂µ Aν ∂ µ Aν + c2 ∂µ Aµ ∂ν Aν }
M4
mit ci ∈
R. Nun ist
Z
!
4
Sfrei [A] =
f ∈ C 2 (M4 )
d x (c1 + c2 ) f (x) f (x) = 0
M4
c1 = −c2
|{z}
:=c
Somit ist
Z
d4 x c {∂µ Aν ∂ µ Aν − ∂µ Aµ ∂ν Aν } (x)
Sfrei [A] =
M4
Z
part. Int.
d4 x c {∂µ Aν ∂ µ Aν − ∂ν Aµ ∂ µ Aν } (x)
=
M4
Z
d4 x c {∂µ Aν − ∂ν Aµ } (x) ∂ µ Aν (x)
=
M4
Die Kombination ∂µ Aν − ∂ν Aµ bildet die Komponenten eines zweifach kovarianten Lorentz-Tensorfeldes F (x)
df.
Fµν (x) = ∂µ Aν (x) − ∂ν Aµ (x)
Dieses hat eine sehr schöne Eigenschaft, nämlich
(k)
∂µ A(k)
ν (x) − ∂ν Aµ (x) = 0
auf ganz M4 (und natürlichen Forderungen an die Komponenten).
Hierfür war wesentlich, dass
Fµν = −Fνµ
gilt, F (x) ist also ein antisymmetrisches Lorentz-Tensorfeld.
Damit wird
Z
d4 x c Fµν (x)∂ µ Aν (x)
Sfrei [A] =
M4
Z
d4 x
=
M4
c
Fµν (x)F µν (x)
2
Aufgabe: Zeigen Sie dies.
F (x) heißt aus Gründen, die alsbald klar sind, der elektromagnetische Feldstärke-Tensor. Die Komponenten dieses
Tensorfeldes sind observabel.
Aufgabe: Ist auch A(x) beobachtbar?
Insgesamt finden wir mit kj ∈
Z
S[A] =
R
(j ∈ {1, 2, 3})
d4 x k1 Fµν F µν + k2 Aλ J λ (x)
M4
Aufgabe: Unter welchen Voraussetzungen darf der Term (∗F )µν F µν vernachlässigt werden?
Das zweifach kovariante Lorentz-Tensorfeld F (x) hat drei Komponententypen: F00 = 0, F0a (x) = −Fa0 (x) und
4
Lagrange-Dichte für das elektromagnetische Potential
35
Fab (x) = −Fba (x) (a, b ∈ {1, 2, 3}). Der Historie ist folgende aus der Perspektive der Speziellen Relativitätstheorie
als unglücklich zu qualifizierende Konvention geschuldet:
~ ∈
Folkloristisch werden die drei Komponenten F0a (x) zu einem Galilei-Vektorfeld E
Komponenten
R3 zusammengefasst, mit
Ea (x) = −F0a (x)
~
E(x)
heißt die elektrische Feldstärke.
~ ∈
Ebenfalls folkloristisch werden die drei Komponenten des (Pseudo-)Vektorfeldes B
R3 eingeführt:
Fab (x) = +abc Bc (x)
~
B(x)
heißt die magnetische Feldstärke (Induktion).
Aufgabe: Lösen Sie Fab = −abc Bc nach Bc auf.
Wir rechnen:
Fµν F µν = Fµν η µα η νβ Fαβ
= F0a η 00 η ab F0b + Fa0 η ab η 00 Fb0 + Fab η ac η bd Fcd
= − 2F◦a δ ab F◦b + Fab δ ac δ bd Fcd
~ Ei
~ + 2hB,
~ Bi
~
= − 2hE,
Aufgabe: Gelingt es Ihnen, die Quellenkopplung durch die elektrische und magnetische Feldstärke auszudrücken?
~ B
~ herleiten, gibt es einen recht trockenen
Bevor wir nun die Bewegungsgleichung für A und die Feldstärken E,
Einschub.
Einschub: Definition der Funktionalabteilung
Sei S ein Funktional auf D(S) und A ∈ D(S). Wir fragen: Wie verändert sich S[A], wenn wir A „etwas“ verändern. Dabei heißt „etwas“ verändern, dass wir A + h ∈ D(S) mit ||h|| klein betrachten. Für ||h|| → 0, sollte
S[A + h] → S[A] sein, sonst wäre S an der Stelle A nicht einmal stetig. Wie aber konvergiert S[A + h] gegen S[A]?
Wir streben eine lineare Approximation an (ein Paradigma der gewöhnlichen Analysis):
S[A + h] ≈ S[A] + L[h] wenn h ≈ 0,
wobei L ein lineares Funktional sei. Selbstverständlich hängt L von S und der Stelle A ab. Diese Abhängigkeit
notieren wir folgendermaßen:
L≡
δS
δA
L heißt die Ableitung des Funktionals S an der Stelle A. Wir werden endlich präziser.
Definition: Ein Funktional S auf D(S) heißt an der Stelle A ∈ D(S) differenzierbar, wenn es einen linearbeschränkten Operator δS/δA gibt (die Funktionalableitung von S an der Stelle A), so dass
S[A + h] − S[A] − δS h 5 ||h|| ε(||h||) ,
δA
für alle h mit ||h|| < δ
Hierbei ist ε eine Nullfunktion: ε(x) → 0 für x → 0.
Bemerkung: Die Normen auf der linken und rechten Seite sind unterschiedlich trotz gleicher Bezeichnung.
Aufgabe: Zeigen Sie Eindeutigkeit der Funktionalableitung. Zeigen Sie, dass ein differenzierbares Funktional erst
recht stetig ist.
4
Lagrange-Dichte für das elektromagnetische Potential
36
Aufgabe: Euler-Lagrange-Gleichungen der Klassischen Mechanik.
In der Literatur finden wir häufig die Schreibweise
δ
S[A],
δA(x)
gelesen so: Die Änderungen des Funktionals S[A] bei Änderung der Funktion A an der Stelle x. Daher der Name
Funktionalableitung. Nun ist diese Funktionalableitung aber selbst ein linear-stetiges Funktional und hat als solches
seine Bedeutung als Anzuwendendes auf geeignete Funktionenräume M ⊃ D(S). Es ist also selbst Element des
zugehörigen dualen Raumes,
δS[A]
∗
∈M
δA
und seine Wirkung kann wie üblich als inneres Produkt notiert werden: Für h ∈ M ist
Z
δ
δ
S[A] h = dz
S[A] h(z)
δA
δA(z)
Aufgabe: Wie erhalten Sie hieraus obige lokale Auswertung der Funktionalableitung (an der Stelle x)?
Ein instruktives Beispiel ist folgendes: Sei S[A] die Zuordnung
S[A] = A(y) ∈
R
(oder
C)
Dann ist
S[A + h] − S[A] = h(y)
Z
≡ dz
δ
S[A] h(z)
δA(z)
Folglich existiert die Funktionalableitung und es gilt die übliche Formel
δA(y)
= δ(y − z)
δA(z)
Uns interessiert hauptsächlich, wie Feldgleichungen (das heißt Bewegungsgleichungen für Felder) aus dem Extremalprinzip der Wirkung folgen. Sei
Z
S[f ] = d4 x L(f (x), ∂µ f (x), x)
Extremalprinzip:
δS[f ]
∂L
∂
∂L
=0
=0 ⇒
−
δf (x)
∂f
∂xλ ∂ ∂f
λ
∂x
Aufgabe: Zeigen Sie dies!
Beispiel:
1
1
L = − η(dΦ, dΦ) − m2 Φ2 + JΦ ,
2
2
∂L
= −m2 Φ + J ,
∂Φ
∂L
= −∂ λ Φ
∂∂λ Φ
⇒ Euler-Lagrange-Gleichung (Feldgleichung)
( − m2 )Φ(x) = −J(x)
Dies ist die sogenannte Klein-Gordon-Gleichung für ein reelles Skalarfeld.
4
Lagrange-Dichte für das elektromagnetische Potential
37
In manchen Anwendungen ist es zweckmäßig, die Funktionalableitung auf die gewöhnliche Ableitung dadurch zurückzuführen, dass S[A+τ h] als Funktion von τ ∈ aufgefasst wird. Dafür definieren wir das Richtungsdifferential
des Funktionals S and der Stelle A durch
R
df.
S[A + τ h] − S[A]
τ →0
τ
∂S[A; h] = lim
sofern der Limes existiert. Beachten Sie, dass ∂S nicht nur von der „Stelle“ A abhängt, sondern auch von der
„Richtung“ h. Die Abhängigkeit des Richtungsdifferentials von der Richtung kann linear sein, muss es aber nicht!
Wenn ∂S[A; h] bezüglich h durch einen linearen Operator zu beschreiben ist,
∂S ! ∂S
h
h≡
∂S[A; h] =
∂A
∂A so nennen wir den linearen Operator
∂S
∂A
über einen geeigneten Funktionenraum die Richtungsableitung.
Der Zusammenhang mit der Funktionalableitung ist folgender:
(I) Wenn (!) S an der Stelle A funktional differenzierbar ist, so existiert erst recht die Richtungsableitung, und
es gilt:
∂S
δS
=
δA
∂A
(II) Existiert (!) ∂S[A; h] in einer Umgebung ||A−A0 || 5 r von A ∀ h, und ist es in h stetig sowie in A gleichmäßig
stetig, so ist S in dieser Umgebung funktional differenzierbar.
Höhere Funktionalableitungen können ohne weitere Probleme eingeführt werden. Es gelten die Ketten- und die
Produktregel. Für Funktionale gilt ein Mittelwertsatz und eine Taylor-Entwicklung mit Restgliedabschätzung.
Aufgabe: Informieren Sie sich hierüber und formulieren Sie die Sachverhalte so präzise wie möglich. Ein Blick
in die Beweiskultur sei empfohlen.
Auf Seite 34 fanden wir:
Z
S[A] =
d4 x k1 Fρσ F ρσ + k2 Aλ J λ
{z
}
|
M4
L(Aρ ,∂σ Aρ ,x)
Zunächst einmal ist
Fρσ F ρσ = Fρσ η ρλ η σκ Fλκ
und
∂Fαβ
∂
∂
∂
=
= (η µα η νβ − η µβ η να )
∂(∂µ Aν )
∂(∂µ Aν ) ∂Fαβ
∂Fαβ
Wir rechnen:
∂L
∂L
∂L
= k2 J µ ,
= (η µα η νβ − η µβ η να )
∂Aµ
∂(∂µ Aν )
∂Fαβ
= (η µα η νβ − η µβ η να ) 2k1 F αβ = 4k1 F µν
Die Feldgleichungen sind somit
k2 J µ (x) − 4k1 ∂λ F λµ (x) = 0
wobei k1 , k2 ∈
R noch unbestimmt sind.
Nun ist
∂λ F λµ = Aµ − ∂ µ (∂λ Aλ )
µ
⇒ 4k1 A
− 4k1 ∂ µ (∂λ Aλ ) = k2 J::µ
::::
4
Lagrange-Dichte für das elektromagnetische Potential
38
Eine Frage die sich hier direkt stellt ist, ob überhaupt eine interessante Information in dem Koeffizienten steckt.
Wir untersuchen diese Frage mit einem strukturellen Vorgriff.
Dieser Vorgriff besteht in der Formulierung von Klassischer Feldtheorie nach Hamilton und ist, salopp geschrieben,
eine nahe liegende Verallgemeinerung von Hamiltons Formulierung der Theorie dynamischer Systeme von Punktteilchen auf dynamische Systeme von Feldern.
Zunächst ist
∂L
= 4k1 F 0µ := π µ
∂(∂0 Aµ )
Insbesondere ist π 0 = 0, weshalb A0 kein dynamischer Freiheitsgrad sein kann. Hierzu später mehr!
Die Hamilton-Funktion ist somit
Z
H = d3 x ~π , Ȧ − L
Es genügt den quellen-freien Fall zu betrachten, also
Z
H = d3 x ~π , Ȧ − k1 Fαβ F αβ
Z
= d3 x ~π , Ȧ + 2k1 (F0a )2 − k1 (Fab )2
Für die kanonisch konjugierten Impulsfelder fanden wir
π 0 = 0 , π c = 4k1 F 0c = 4k1 Fc0 = −4k1 F0c = πc
Also ist
~˙ − ∇A0 ) ⇒ h~π˙ , Ai
~˙ = − 1 h~π , ~π i + h~π , ∇A0 i
~π = −4k1 (A
4k1
Weiterhin gilt
hF0a , F0a i =
1
4k1
2
h~π , ~π i
Z
1 1
3
2
⇒H= d x −
h~π , ~π i + h~π , ∇A0 i − k1 (Fab )
2 4k1
Z
1 1
3
~
~
= d x −
h~π , ~π i − 2k1 h∇ × A, ∇ × Ai + h~π , ∇A0 i
2 4k1
Wir müssen uns Klarheit über den letzten Term verschaffen.
Da A0 kein dynamischer Freiheitsgrad ist (π 0 = 0), liefert die Euler-Lagrange-Gleichung für ν = 0 statt einer
Bewegungsgleichung (zweiter Ordnung in den Zeitableitungen) folgende Einschränkung im quellen-freien Fall:
∂a F a0 = ∂a (−
1 a !
π )=0
4k1
~ · ~π = 0.
also die Einschränkung ∇
Partielle Integration des letzten Terms in H liefert
Z
Z
!
3
d xh~π , ∇A0 i = − d3 xh∇ · ~π , A0 i = 0
Wir finden somit
Z
1 1
3
~
~
~
~
H= d x −
h~π , ~π i − 2k1 h∇ × A, ∇ × Ai
2 4k1
4
Lagrange-Dichte für das elektromagnetische Potential
39
Der Integrand ist gerade die Energiedichte der quellen-freien (überhaupt freien) Theorie.
Daher muss
1 1
~ ∇ × Ai
~ =0
h~π , ~π i − 2k1 h∇ × A,
2 4k1
⇒ k1 < 0
df.
H=−
Ansonsten ist k1 unbestimmt und wir dürfen die Felder zweckmäßig redefinieren. Zum Beispiel k1 = − 41 . Dann ist
1
1
~ ∇ × Ai
~
H = + h~π , ~π i + h∇ × A,
2
2
Der Koeffizient k2 kann (gegebenenfalls nach geeigneter Feldredefinition) in der externen Quelle (Stromdichte)
absorbiert werden. Als Resultat finden wir
Z
1
αβ
λ
4
(∗)
S[A] =
d x − Fαβ F + Aλ J
4
M4
~ und B
~ aus.
Aufgabe: Drücken Sie H durch E
Aufgabe: Warum fehlen Terme wie c[2] Aλ Aλ , c[0] (Aλ Aλ )2 , c[−4] (Fαβ F αβ )2 , ...?
Aus der Maxwell-Wirkung (∗) folgen die berühmten und überaus mächtigen Maxwell-Gleichungen mit Quellen:
Aλ − ∂ µ (∂λ Aλ ) = −J µ
Die nicht manifest Lorentz-kovariante Zerfällung geht so:
Wir haben zunächst die Gleichungen
(
∂λ F λµ = −J µ
F0a = −Ea , Fab = abc Bc
~ =ρ
µ = 0 : ∂a F a0 = −J 0 ⇔ ∂ a Fa0 η 00 = −J 0 ⇔ ∇ · E
~˙ + ∇ × B
~ = J~
µ = b : Für b ∈ {1, 2, 3} finden wir ähnlich ∂λ F λb = −J b ⇔ −E
Bemerkung: δ 0 = η 0λ ∂λ = −∂0
Wir haben also vier Bewegungsgleichungen
~ = ρ , rotB
~ −E
~˙ = J~
divE
und sechs definierende Gleichungen
−Ea = F0a , abc Bc = Fab
Aus nostalgischen Gründen formulieren wir die definierenden Gleichungen folgendermaßen um:
~ = rotA
~
abc Bc = Fab ⇒ B
~ =0
⇒ divB
~ = −A
~˙ + gradA0
−Ea = F0a ⇒ E
~ +B
~˙ = ~0
⇒ rotE
Insgesamt finden wir somit
~ =ρ,
divE
~ =0,
divB
~ −E
~˙ = J~
rotB
~ +B
~˙ = ~0
rotE
Aufgabe: Kovariantisieren Sie die definierenden Gleichungen
5
Lösungstheorie
40
5 Lösungstheorie
5.1 Quellenfreie Theorie
Wir beginnen mit
Φ(x) = 0
Offenbar handelt es sich hierbei um eine lineare partielle Differentialgleichung 2. Ordnung mit konstanten Koeffizienten. Sie wird als homogene (weil quellenfreie) Wellengleichung in der Literatur geführt. Eine algebraische
Charakterisierung funktioniert so: Betrachte
l
X
Mab ∂a ∂b Φ(x0 , . . . , xl ) = 0
a,b=0
wobei
M ∈ R(l). Mit dieser Matrix können wir andererseits die quadratische Form
F(x0 , . . . , xl ) =
l
X
Mab xa xb
a,b=0
bilden. Setzen wir F = const. , so beschreibt sie in 2 Dimensionen die üblichen Kegelschnitte, in 3 Dimensionen
Kegelschnittflächen und Analoges in höheren Dimensionen.
Nun unterscheiden sich Hyperbeln von Ellipsen geometrisch sehr, und welche der beiden Möglichkeiten realisiert
ist, hängt von den Vorzeichen der stets existierenden Eigenwerte der Matrix M ab. In diesem Fall ist M = η, die
Wellengleichung ist also mit einer hyperbolischen Form assoziiert. Und nach dieser Form wird die Wellengleichung
auch als hyperbolische Differentialgleichung bezeichnet.
Aufgabe: Geben Sie eine algebraische Charakterisierung der Schrödinger-Gleichung an.
Es wird sich herausstellen, dass die algebraische Charakterisierung extrem relevant für den physikalischen Inhalt
einer Theorie und sogar für deren Konsistenz ist.
5.1.1 Die eindimensionale Wellengleichung
Für eine Raumdimension haben wir
∂2
∂2
Φ(x0 , x1 ) = 0
− 2+
∂x0
∂x21
df.
Wir nennen U± = x1 ± x0 und betrachten Funktionen
C 2 (M2 ) 3 f : M2 →
K,
(x0 , x1 ) → f (U± )
Wegen der speziellen Abhängigkeit gilt
d2 f
∂2f
=
2
2 ,
∂x0
dU±
d2 f
∂2f
=
2
2
∂x1
dU±
Somit löst jede solche Funktion die Wellengleichung in einer Raumdimension.
Offenbar beschreibt f (U− ) eine Funktion, die sich ohne Veränderung ihrer Form, also starr, mit der konstanten Geschwindigkeit c von links nach rechts verschiebt, und f (U+ ) entsprechend.
t=
t=0
∆x
∆x
c
x
5
Lösungstheorie
41
Viele unter Ihnen werden sich unter einer „Welle“ etwas ganz anderes vorgestellt haben, nämlich irgendeine raumzeitliche periodische Struktur. Wir kommen hierauf zurück.
Zunächst: Wir bezeichnen die mit konstanter Geschwindigkeit laufenden allgemeinen Lösungen als Wellenzüge.
Da die Wellengleichung linear ist, lassen sich mehrere Wellenzüge superponieren (überlagern). Das ist nicht sonderlich aufregend, solange sie die gleiche Laufrichtung haben:
t=0
t>0
t=0
t>0
x
Gegenläufige Lösungen durchdringen sich ungestört. In diesem Fall ändert sich die Gestalt der Gesamtlösung in
charakteristischer Weise:
Die allgemeine Lösung ist eine Überlagerung:
g(x0 , x1 ) = f (+) (U− ) + f (−) (U+ )
Da die Wellengleichung eine Differentialgleichung von zweiter Ordnung in der Zeit ist, bestehen die zur Bestimmung
einer eindeutigen Lösung notwendigen Anfangsdaten aus Anfangswerten g(x0 , x1 ) und Anfangsgeschwindigkeiten
ġ(x0∗ , x1 ).
Aufgabe: Wann reicht die Angabe der Anfangswerte?
Interessant (später) sind insbesondere Lösungen der Form
cos(k U± ) = cos(kx ± kct)
n
o
= Re ei(kx±kct) ,
k>0
Ihre Periodizität in der Phase U± führt zu einer doppelten Periodizität in Zeit und Ort. Zu gegebener Zeit t∗ ist
sie nämlich räumlich periodisch mit der Wellenlänge
λ=
2π
k
und am festen Ort x∗ zeitlich periodisch mit der Schwingungsdauer
T =
2π
λ
=
ck
c
In der Zeit T schiebt sich die Lösung gerade um λ weiter und ist dann natürlich nicht mehr von der unverschobenen
Lösung zu unterscheiden.
5
Lösungstheorie
42
Weiterhin nennen wir
ν=
1
c
ck
= =
T
λ
2π
die Frequenz und
ω = 2πν = ck
die Kreisfrequenz dieser Lösung. Die Größe k wird als Wellenzahl bezeichnet. Offenbar gilt für diese Lösung
n
o
cos(k U± ) = Re ei(kx±ωt)
Der Ursprung des Koordinatensystems ist natürlich willkürlich:
cos k(x − x∗ ) ± ω(t − t∗ ) = cos(kx ± ωt + ϕ)
wobei ϕ der Phasenwinkel heißt. Für beliebiges A ∈
o
n
o
n
|A| Re ei(kx±ωt+ϕ) = Re Aei(kx±ωt)
C ist damit auch
eine Lösung der Wellengleichung.
Addieren wir die beiden gegenläufigen Wellen cos(k U± ), so erhalten wir
cos(k U+ ) + cos(k U− ) = 2 cos(kx) cos(ωt)
Diese Lösung läuft nicht mehr, sondern steht. Sie heißt stehende Welle.
Aufgabe: Betrachten Sie k → −k , ω → −ω.
Und: k > 0 , ω → −ω. Diskutieren Sie die Physik!
Die gerade betrachteten Lösungen entsprechen unserer naiven Vorstellung von Wellen. Zunächst handelt es sich
hierbei aber um höchst spezielle Lösungen der Wellengleichung. Sie sind aber trotzdem die wichtigsten, denn jeder
Wellenzug kann als Superposition periodischer Lösungen dargestellt werden.
5.1.2 Die mehrdimensionale Wellengleichung
Für zum Beispiel drei räumliche Variablen, x = (x0 , ~x) mit ~x = (x1 , x2 , x3 ) ist
!
Φ(x) = (−∂02 + ∆)Φ(x0 , ~x) = 0
Wir beginnen mit einem speziellen Lösungstyp, nämlich den ebenen Wellen, die sehr direkt den Lösungen der
(1+1)-dimensionalen Wellengleichung entsprechen.
Für jeden beliebigen Lorentz-Vektor k = (k 0 , ~k) mit k 0 = ±|~k| und ~k 6= ~0 lösen die Funktionen
n
o
f (x0 , ~x) = Re eiη(k,x)+iϕ
die Wellengleichung. Wir schreiben η(k, x) =: k · x. In der Tat gilt ja
−∂02 f = (k0 )2 f , ∆f = −|~k|2 f ⇒
(k0 )2 − (~k)2 = 0
was gerade für k 0 = ±|k| erfüllt ist.
Wie sehen ebene Wellen aus? Zu einem festen Zeitpunkt x0 = x0∗ gilt doch
f (x0∗ , ~x) = const.
∀~x ∈
R : h~k, ~xi = const.
5
Lösungstheorie
43
Das sind aber alle Punkte auf einer Normalebene zu ~k. Jede dieser
Ebenen heißt Wellenfront, da f (x0∗ , ~x) auf ihnen konstant ist.
Lassen wir x0 laufen, so bewegen sich die Wellenfronten parallel und mit der Geschwindigkeit c längs ~k, und zwar in Richtung
~kˆ ≡ ~k für k 0 > 0 und entgegengesetzt zu ~kˆ für k 0 < 0. Für ebene
|~
k|
Wellen gelten folgende Bezeichnungen: ~k heißt Wellenvektor, |~k|
ˆ
heißt Wellenzahl und ~k Ausbreitungsrichtung. Für Wellenlängen gilt
2π
wieder λ = |~k| und für die Frequenz
ν=
~k
x0 = const.
c
c |k 0 |
=
2π
λ
Ebene Wellen spielen eine fundamentale Rolle für die allgemeine Lösung der Wellengleichung.
Ein anderer wichtiger Lösungstyp ist durch die sogenannten Kugelwellen gegeben
o
n
0 0
1
~
f (x0 , ~x) =
Re ei(−k x ±|k||~r|)
|~r|
Dass diese Funktionen Lösungen der quellenfreien Wellengleichung darstellen, zeigen wir am einfachsten in Kugelkoordinaten. Offenbar gilt:
1 ∂
2 ∂f
∆f (x0 , |~x|) =
|x|
|~x|2 ∂|~x|
∂|~x|
Wir rechnen:
∂f
i|~k|
1
−i(k0 x0 ∓|~
k||~
x|+ϕ)
= + Re
±
− 2 e
∂|x|
|~x|
|~x|
−i(k0 x0 ∓|~
k||~
x|+ϕ)
2 ∂f
~
= + Re
± i|k||~x| − 1 e
|~x|
∂|~x|
∂
−i(k0 x0 ∓|~
k||~
x|+ϕ)
2 ∂f
2
~
|~x|
= − Re |k| |~x| e
∂|~x|
∂|~x|
⇒ ∆f = −|~k|2 f , ∂0 f = −(k 0 )2 f
Insgesamt erhalten wir
(k 0 )2 − |~k|2 f = 0 für (k 0 )2 = |~k|2
Wie sehen Kugelwellen aus?
(1) Die Wellenfronten werden bestimmt durch
|~k||~x| − k 0 x0 = const.
Es handelt sich also um Kugelflächen um den Ursprung. Besitzen k 0 und ±|~k| das gleiche Vorzeichen, bewegen
sie sich mit konstanter Phasengeschwindigkeit c von Ursprung fort, andernfalls in den Ursprung hinein. Daher
werden diese Lösungstypen auslaufende beziehungsweise einlaufende Kugelwellen genannt.
den Abstand zwischen zwei aufeinanderfolgender Nulldurchgänge ver(2) Wir können als Wellenlänge λ = |2π
~
k|
stehen. Kugelwellen sind allerdings nicht räumlich periodisch. Es gilt immer noch
f (|~x|) = 0 ⇒ f (|~x| +
Z · λ) = 0
hingegen nicht mehr
f (|~x| +
Z \ {0} · λ) = f (|~x|)
Aufgabe: Fertigen Sie eine Skizze an.
5
Lösungstheorie
44
5.1.3 Vektorwellen
~ (x) ein Vektorfeld mit V
~ (x) = P3 V j (x) ej Wir betrachten
Sei V
j=1
~ (x) = ~0
V
~ genügt für sich dieser homogenen Wellengleichung, und folglich liefert der Ansatz
Jede Komponente von V
n
o
(0)
(0)
Vj = Re Vj eik·x , Vj ∈ , j ∈ {1, 2, 3}
C
eine Lösung, falls nur |k 0 | = |~k| gilt.
Der komplexe Vektor V~(0) heißt Amplitudenvektor. Diesen können wir in jede Orthonormalbasis entwickeln, insbesondere auch in folgender:
ˆ ˆ df. ~k
e~3 = ~k , ~k =
|~k|
(0)
(0)
(0)
Damit bedeutet V3 die Amplitude in Ausbreitungsrichtung und V1 , V2 sind die Amplituden ⊥ zur Aus~ (0) in Richtung von ~k, V
~ (0) k ~k, so schwingt die Vektorwelle ausschließlich in
breitungsrichtung. Liegt speziell V
Ausbreitungsrichtung. In diesem Fall sprechen wir von einer longitudinalen Welle.
~ (0) ⊥ ~k, so finden die Auslenkungen senkrecht zur Ausbreitungsrichtung statt und wir sprechen
Gilt hingegen V
von einer transversalen Welle. Wir werden später sehen, dass freie elektromagnetische Wellen stets transversal sind.
Transversale Wellen besitzen ein weiteres Charakteristikum, die sogenannte Polarisation, die mit der relativen
(0)
(0)
Phase der komplexen Amplituden V1 und V2 zusammenhängt,
n
o
~ = Re |V (0) | ei(kx+ϕ1 ) e~1 + |V (0) | ei(kx+ϕ2 ) e~2
V
1
2
Für ϕ1 = ϕ2 (...) ist
n
o
~ = |V (0) |e~1 + |V (0) |e~2 Re ei(kx+ϕ)
V
1
2
und es gibt genau eine wohldefinierte Richtung ~e auf der
Normalebene ⊥ ~k, in der die transversale Welle unabhängig von x = (x0 , ~x) schwingt. Eine solche Welle heißt
linear polarisiert, ihre Amplitude ist durch
q
~ (0) | = V (0) V (0)∗ + V (0) V (0)∗
|V
1
1
2
2
(0)
gegeben, wobei Vj
∈
~k
C für j ∈ {1, 2}.
(0)
(0)
(0)
Eine weiter Möglichkeit ist gegeben, wenn |V1 | = |V2 | = |V3 | und ϕ2 = ϕ1 ± π2 . In diesem Fall haben wir
~ = |V (0) | cos(kx + ϕ1 ), sin(kx + ϕ1 ), 0 T
V
~ = (V1 , V2 , 0)T eine
Die Schwingungsrichtung ist nicht länger unabhängig von der Phase, vielmehr beschreibt V
rechts
π
~
Kreisspirale mit Achse k und Ganghöhe λ, die für ∆ϕ = ± 2 als links –Spirale durchlaufen wird. Bei fixiertem ~x
durchläuft sie mit konstanter Winkelgeschwindigkeit ω = ck 0 einen Kreis mit Radius |V (0) |. Entsprechend sprechen
wir von rechts
links –zirkular polarisierten Wellen.
Aufgabe: Zeigen Sie: Ist eine transversale Welle weder linear noch zirkular polarisiert, so ist sie elliptisch polarisiert.
5
Lösungstheorie
45
5.1.4 Quellenfreie elektromagnetische Wellen
Aus der Maxwell-Wirkung und den Definitionsgleichungen für E-, und B-Feld folgten die sogenannten MaxwellGleichungen
~ =ρ,
divE
~ =0,
divB
~ −E
~˙ = J~
rotB
~ +B
~˙ = ~0
rotE
Quellenfrei bezieht sich auf die Abwesenheit von elektrischen Ladungen, also ρ = 0 und J~ = ~0.
Da die Maxwell-Gleichungen linear sind, werden der Real-, und der Imaginärteil komplexer Lösungen in ihnen
nicht gemischt. Finden wir also, dass bereits die komplexen Wellen Lösungen dieser Gleichungen sind, so können
wir durchgängig mit ihnen rechnen und den Übergang zum Realteil erst am Endergebnis vollziehen. Noch wissen
wir aber nicht, ob elektromagnetische Wellen tatsächlich die Maxwell-Gleichungen lösen.
Drei Vorgehensweisen erscheinen evident:
(1) Wir untersuchen, ob die kovarianten Bewegungsgleichungen für Aµ Wellenlösungen haben. Dies wird im
Moment noch dadurch erschwert, dass wir die in diesen Gleichungen vorhandene eichtheoretische Redundanz
noch nicht fixiert haben.
(2) Wir leiten Differentialgleichungen zweiter Ordnung zu der Zeit für E, B her und untersuchen deren Lösungstypen.
(3) Wir setzen einfach Wellengleichungen an und prüfen die Konsistenz dieses Ansatzes mit den quellenfreien
Maxwell-Gleichungen.
Aufgabe: Arbeiten Sie alle Strategien en detail aus.
Wir verfolgen (3), also
~
~ (0) eik·x , B(x)
~
~ (0) eik·x
E(x)
=E
=B
Wir finden
~ = 0 ⇒ +ih~k, Ei
~ =0
divE
~˙ + rotB
~ = ~0 ⇒ +i k0 E
~ + ~k × B
~ = ~0
−E
~ = 0 ⇒ +ih~k, Bi
~ =0
divB
~˙ + rotE
~ = 0 ⇒ −i k0 B
~ − ~k × E
~ = ~0
B
(1)
(2)
(3)
(4)
Aus (1) und (3) folgt, dass die ebenen Wellen transversal sein müssen, um die Maxwell-Gleichungen zu erfüllen.
Die Gleichungen (2) und (4) multiplizieren wir vektoriell (folkloristisch für Kreuzprodukt) mit ~k und setzen sie
dann ineinander ein. Wir erhalten
)
(
~k × (~k × B)
~ = −k0~k × E
~ = −(k0 )2 B
~
~ = ~0
− ko2 + |~k|2 B
⇒
2
2
~ = ~0
~k × (~k × E)
~ = −(k0 )2 E
~
− ko + |~k| E
Somit: Transversale ebene Wellen lösen die Maxwell-Gleichungen genau dann, wenn
k0 = ±|~k|
gilt. Dies ist aber genau der in den vorigen Abschnitten geforderte Zusammenhang.
Interessant ist hierbei, dass elektromagnetische Wellen, einmal angeregt, sich im Vakuum ungedämpft ausbreiten. Das ist aber noch nicht die gesamte Information, die in den quellfreien Maxwell-Gleichungen steckt. Aus der
Definitionsgleichung (4) folgt ja direkt, dass
~
~ = 1 ~k × E
B
k0
(∗)
5
Lösungstheorie
46
~ nicht nur auf ~k senkrecht, sondern auch auf E.
~ Und zwar gilt diese Aussage für den Real-, als auch
Also steht B
für den Imaginärteil der komplexen Wellenlösung getrennt.
Es folgt unmittelbar
~
1 ~ ~
~ = |k| |E|
~
|k||E| sin ^(~k, E)
|k0 |
|k0 |
~
|~k|
|B|
=
⇒
~
|k0 |
|E|
~ =
|B|
~ und B-Feld
~
Insbesondere impliziert (∗), dass der Polarisationszustand von E-,
der gleiche ist.
5.1.5 Die allgemeine Lösung der homogenen Wellengleichung
Wie Sie bereits wissen, erlaubt die Fourier-Transformation die Darstellung jeder (transformierbaren) Funktion f (x)
.
durch kontinuierliche Überlagerung von periodischen Funktionen der Wellenlänge λ = |2π
~
k|
Gleichweise bedeutet
Z
d4 k ik·x e
f (x) =
e f (k)
(2π)2
dass jede Fourier-transformierbare Funktion durch eine kontinuierliche Überlagerung von ebenen Wellen erzeugt
werden kann, wobei kµ ∈ (−∞, +∞) für µ ∈ {0, 1, 2, 3}. Wir stellen nun den Zusammenhang zu Lösungen der
homogenen Wellengleichung her. Um eine Lösung der homogenen Wellengleichung zu bekommen, dürfen wir nur
solche ebene Wellen überlagern, die selbst Lösungen sind, für die also |k0 | = |~k| gilt. Folglich muss für die FourierAmplitude folgendes gelten:
fe(k) = fe(−) (~k) δ (1) (k0 + |~k|) + fe(+) (~k) δ (1) (k0 − |~k|)
wobei fe(∓) ansonsten frei wählbar sind. Somit
f (x0 , ~x) =
Z
d3 k n e ~ i(h~k,~xi+|~k|x0 ) e ~ i(h~k,~xi−|~k|x0 ) o
f(−) (k) e
+ f(+) (k) e
(2π)2
Dies ist die allgemeine Lösung der homogenen Wellengleichung. Speziell für eine Raumdimension besteht diese
genau aus allen (transformierbaren) Funktionen der Gestalt
f (x0 , ~x) = f (+) (x − x0 ) + f (−) (x + x0 )
in denen wir unsere Wellenzüge wiederentdecken.
Aufgabe: Zeigen Sie, dass dieses Resultat immer in Ausbreitungsrichtung gilt.
Wir hätten auch so vorgehen können:
Z
Z
d4 k ik·x 2
d4 k ik·x e
e
f
(k)
=
0
⇒
e
i η(k, k) fe(k) = 0
f (x) = 0 ⇒ 2
(2π)
(2π)2
Aufgabe!
η(k, k)fe(k) = 0
Dass heißt fe(k) muss überall verschwinden mit Ausnahme der Nullstellen von η(k, k). Auf dieser Nullstellenmenge
kann fe(k) aber nicht identisch verschwinden, denn dann wäre ja fe ≡ 0 und f wäre die triviale Lösung. Dies
impliziert wiederum (zeigen Sie dies), dass
fe(k) = fe(−) (~k) δ (1) (k0 + |~k|) + fe(+) (~k) δ (1) (k0 − |~k|)
also unser altes Resultat.
5
Lösungstheorie
47
Wie lassen sich diese Resultate nun auf die quellenfreien Maxwell-Gleichungen übertragen. Nicht direkt, denn
die Bewegungsgleichungen sind ja von der Form
Aµ − ∂µ (∂ · A) = 0
Wir Fourier-transformieren in gewohnter Weise und erhalten als Bestimmungsgleichung für die Fourier-Amplitude,
beziehungsweise deren Komponenten:
eλ (k) = 0
η(k, k) ηµλ − kµ k λ A
Für η(k, k) 6= 0, muss folgendes gelten:
λ
λ
df.
eλ (k) = 0 , wobei P (⊥)µ (k) = ηµλ −
P (⊥)µ (k)A
kµ k λ
η(k, k)
Im Kern des Projektionsoperators P (⊥) liegen die sogenannten longitudinalen Fourier-Amplituden, im Bild die
transversalen Anteile. Die Namensgebung ist folgendem Umstand geschuldet:
λ
eλ (k) = 0 ⇔ A
eλ (k) ∼ kλ
P (⊥)µ A
Für η(k, k) = 0 finden wir (und k 6= 0)
eλ (k) = 0
kλ A
e ∼ k wieder eine Lösung, allerdings
Die Analyse dieser Gleichung ist ein wenig komplizierter. Zunächst einmal ist A
e
e
die triviale, da η(A, A) = 0. Eine interessante Lösung ist
eµ (k) = P ⊥ (k) η(k, k) e
A
aλ (k)
µ
Aufgabe: Welche Forderung stellen Sie an e
a(k)?
Für η(k, k) 6= 0 finden wir also lediglich longitudinale Fourier-Amplituden, während für η(k, k) = 0 ausschließlich transversale vorliegen. Die Frage ist nun, ob sowohl longitudinale als auch transversale Fourier-Amplituden
physikalisch relevant sind. Insbesondere gilt ja für die longitudinalen Fourier-Amplituden
e
η(k, A(k))
6= 0 für η(k, k) 6= 0
e
Nun ist aber die algebraische Bestimmungsgleichung für A(k)
invariant unter der Ersetzung
eµ (k) → A
eµ (k) + kµ χ
e0µ (k)
A
e(k) =: A
Dies ist der algebraische Ausdruck für die Redundanz, die sich aus der Ladungserhaltung ergibt.
Wir finden
e0 (k) = η k, A(k)
e
η k, A
+η(k, k) χ
e(k)
|
{z
}
6=0
Da χ
e(k) beliebig ist (bis auf übliche Qualifikationen), können wir insbesondere die folgende Wahl treffen:
1
e
χ
e(k) = −
η k, A(k)
, η(k, k) 6= 0
η(k, k)
und erreichen so immer, dass
e0 (k) = 0
η k, A
gilt. Die Redundanz lässt sich also derart fixieren, dass die longitudinalen Fourier-Amplituden allesamt zum Verschwinden gebracht werden können. Sie stellen keine physikalischen Freiheitsgrade dar, können also keine Physik
tragen. Die Forderung
e
η k, A(k)
=0
5
Lösungstheorie
48
kann somit für alle Fourier-Amplituden gestellt werden. Die dynamischen Freiheitsgrade der Maxwell-Theorie sind
transversale Polarisationen.
Mit dieser Forderung wird die algebraische Bestimmungsgleichung
(
e
η (k,
k)A(k)
=0
e
η k, A(k)
=0
Die inverse Fourier-Transformation liefert als Bewegungsgleichung für die transversalen Polarisationen
(
Aµ (x) = 0
∂λ Aλ (x) = 0
Die zweite Gleichung ist ein Restriktion, keine dynamische Gleichung. Diese Restriktion heißt Lorentz-Eichung,
A(x) wird Eichpotential oder Eichfeld genannt. Die Lorentz-Eichung erlaubt offenbar, eine Komponente von A(x)
zu eliminieren und durch die anderen auszudrücken.
Wir fragen nun, ob die Lorentz-Eichung alle Redundanzen in der Beschreibung fixiert, die wir uns zu Gunsten
einer manifest Lorentz-kovarianten Formulierung eingehandelt haben?
Die in Frage kommenden Transformationen von A(x) müssen konsistent mit der geforderten Quellenerhaltung
sein, denn diese verursacht ja physikalisch die Redundanz. Daher kommen lediglich Transformationen der Form
A → A + dχ0
in Frage. Die Funktion χ0 nun gehorcht der homogenen Wellengleichung, χ0 (x) = 0. Welche Anfangsbedingungen
wählen wir? χ(t0 , ~x) sei Lösung von
~ 0 , ~x)
∆χ0 (t0 , ~x) = −divA(t
und für die erste Zeitableitung setzen wir
χ̇0 (t0 , ~x) = −A0 (t0 , ~x)
(c = 1)
df.
Die durch f = A0 + χ̇0 definierte Funktion gehorcht
f (x) = 0
Die Anfangsbedingungen sind
f (t0 , ~x) = 0
f˙(t0 , ~x) = Ȧ(t0 , ~x) + χ̈0 (t0 , ~x) = 0
~ (Lorentz-Eichung) und χ0 gehorcht der homogenen Wellengleichung mit Anfangswert ∆χ0 =
denn Ȧ0 = divA
~ Die eindeutige Lösung der homogenen Wellengleichung für f mit den genannten Anfangsbedingungen ist
−divA.
f (x) = 0 ⇒ χ̇0 = −A0
∀t ∈
R
Daher erlaubt die Transformation A → A + dχ0 die Komponente A0 zu eliminieren. Diese nachfolgende Eichung
(setzt die Lorentz-Eichung voraus) heißt auch eingeschränkte Eichung. Die Wahl A0 = 0 ∀x ∈ M4 wird Temporale
Eichung genannt. Damit ist sämtliche Redundanz eliminiert und wir verbleiben mit zwei dynamischen Freiheitsgraden in der quellenfreien Theorie!
Aufgabe: Beweisen Sie die letzte Aussage.
Aufgabe: Führen Sie die Argumentation im Fourier-Raum durch.
Referat: Eichungen
5
Lösungstheorie
49
5.2 Absorption und Emission
Wir beginnen mit einer heuristischen Vorbetrachtung anhand von
Φ(x) = ρ(x) , x = x0 , ~x
Wir können diese Gleichung so lesen: Φ hängt funktional von der Quelle ab, also
Φ[ρ] = f (x)
Wegen des Superpositionsprinzips handelt es sich in der Tat um ein lineares Funktional
Φ[ρ1 + ρ2 ] = Φ[ρ1 ] + Φ[ρ2 ]
Wir machen daher den folgenden Ansatz:
Z
Φ[ρ](x) =
d4 y G(x, y) ρ(y)
M4
mit einem unbekannten bilokalen Objekt G, dessen mathematische Qualifikationen noch im Dunkeln liegen.
Einsetzen in die Bewegungsgleichung liefert
Z
x Φ[s](x) = x
d4 y G(x, y) ρ(y)
M4
Z
!
=
d4 y ρ(y) x G(x, y) = ρ(x)
M4
::::::::::::::::::::
Z
d4 y ρ(y) δ (4) (x − y)
=
M4
::::::::::::::::::::
bel. Quellen
x G(x, y) = δ (4) (x − y)
Die Raumzeit-Homogenität von M4 erlaubt folgende Notation:
x G(x − y) = δ (4) (x − y)
Es handelt sich bei G um eine Distribution, die durch obige Gleichung bestimmt wird. Die Distribution G ist ein
alter Bekannter, nämlich das Dirac-Maß.
In der Physik schreiben wir lax
Z
Φ(x) =
d4 y G(x − y) ρ(y)
M4
für die Lösung der inhomogenen Wellengleichung.
Vorsicht: Diese Beschreibung bedingt Φ[0](x) = 0. Dabei handelt es sich doch gerade um die Lösungen der
quellenfreien Theorie! Im Moment sollten wir also besser folgenden Ansatz notieren:
Z
Φ[ρ](x) = Φ[0](x) +
d4 y G(x − y) ρ(y) , wobei Φ[0](x) = 0 gilt.
M4
Andererseits müssen Wellenzüge an irgendeinem Raumzeitpunkt von einer Quelle generiert worden sein. Lassen
Sie uns im Moment vereinfacht annehmen, dass ρ(x) die einzige Quelle in M4 ist (insbesondere zu allen Zeiten).
Dann wäre es physikalisch konsistent in diesem Fall Φ[0] = 0 zu setzen. Eine mathematische Begründung hierfür
überlegen wir uns später. Wie interpretieren wir nun die Distribution G(x − y)? Zunächst einmal haben wir zwei
Raumzeitpunkte x, y ∈ M4 . Am Raumzeitpunkt x fragen wir den Wert des Feldes Φ ab. Dies ist noch kein
physikalischer Messprozess. Dieser wird ja in der Wirkung durch die Vertexdichte
Z
ρa (x)Φ(x) =
d4 x ρa (x) G(x − y) ρe (y)
M4
5
Lösungstheorie
50
beschrieben. Hierbei bezeichnet ρa die zu einem Absorber gehörende Quelldichte (Ladungsdichte) und ρe die zu
einem Emitter gehörende. Nun hatten wir aber angenommen, dass nur eine Quelle ρ in M4 existiert. Außerdem
ist die Quellenankopplung minimal. Daher schreiben wir
ρ = ρa + ρe
Für die Vertexdichte finden wir somit
Z
ρ(x)Φ(x) =
d4 y ρ(x) G(x − y)ρ(y)
M4
Der Einfachheit halber nehmen wir an, dass Emitter (Quelle) und Absorber (Senke) im Hausdorff Sinn getrennt
sind in M4 , sagen wir
supp ρe = [ze − εe , ze + εe ]
supp ρa = [za − εa , za + εa ]
mit supp ρe ∩ supp ρa = {∅}, wobei wir uns ρe und ρa hinreichend gut um ze und za lokalisiert denken.
Nun macht es sicherlich Sinn zu fordern, dass ein Absorber (Detektor) ausschließlich dann ein Signal registriert,
wenn dieses zuvor emittiert wurde. Diese Forderung nach Kausalität sagt uns, dass die Kombination
ρa (x) G(x − y) ρe (y)
(∗)
nur dann von Null verschieden sein sollte, wenn x0 > y 0 . Diese Einschränkung kann aber weder in ρa noch in ρe
kodiert sein, da diese lokale Funktionen sind. Das einzige bilokale Objekt ist die Distribution G(x − y). Damit (∗)
sinnvoll ist, muss also gelten, dass
G(x − y) = θ(x0 − y 0 ) G> (x − y) + f (x − y)
Hierbei ist die Distribution
(
1 für x0 > 0
0 df.
θ(x ) =
0 sonst
und f bezeichne eine Distribution, für die (∗) verschwinde.
Folgendes liegt nahe:
f (x − y) = θ(y 0 − x0 ) G< (x − y)
Die Distribution
df.
Gret (x, y) = θ(x0 − y 0 ) G> (x − y)
heißt retardierende Green-Funktion, die Distribution
df.
Gav (x, y) = θ(y 0 − x0 ) G< (x − y)
heißt avancierte Green-Funktion.
Effektiv haben wir dann für (∗)
ρa (x) Gret (x, y) ρe (y)
Nun gibt es aber auch die Kombination
ρe (x) G(x − y) ρa (y)
Dies macht offenbar nur Sinn für x0 < y 0 , daher haben wir
ρe (x) Gav (x, y) ρa (y)
5
Lösungstheorie
51
Schließlich verlangt die Lorentz-Invarianz der Wirkung die Vertexdichte über M4 aufzuintegrieren:
Z
Z
Z
4
4
d x ρ(x) Φ(x) =
d x
d4 y ρ(x) G(x − y) ρ(y)
M4
M4
M4
Wir sehen, die Unterscheidung in Emitter und Absorber macht keinen Sinn. In beiden Fällen wird von Quellen
gesprochen. Obige Überlegungen liefern uns aber eine Interpretation der Distribution G(x − y).
Nur die Distribution G hängt vom Raumzeit-Abstand zwischen Emitter und Absorber ab. Folglich beschreibt
G, wie sich die Information, dass ein Emitter am Raumzeit-Punkt y ∈ M4 sitzt, zum Absorber hin am RaumzeitPunkt x ∈ M4 ausbreitet (oder umgekehrt). Dieser Informationsausbreitung entspricht aber gerade die Ausbreitung
des emittierten Feldes selbst. Damit ist die essentielle Felddynamik in G kodiert. Distributionen, die die raumzeitliche Ausbreitung von Feldern zwischen Emissions-, und Absorptionsereignis beschreiben sind von grundlegender
Bedeutung für das Verständnis von Wechselwirkungen in der Natur!
Wir beenden unsere heuristische Betrachtungsweise mit folgender Bemerkung: Offenbar gilt
[G] = E 2
Weiterhin wissen wir, dass sich ein masseloses Feld ausschließlich auf dem Lichtkegel ausbreitet.
Dies und unsere bisherigen heuristischen Betrachtungen legen nahe, dass
G ≶ (x − y) =
1 (1)
δ
(x − y)2
2π
Wir haben somit
1
1
G(x − y) = θ(x0 − y 0 ) δ (1) (x − y)2 + θ(y 0 − x0 ) δ (1) (x − y)2
2π{z
2π{z
|
} |
}
Gret (x,y)
Gav (x,y)
Aufgabe: Zeigen Sie, dass die Zerlegung von G in retardierte und avancierte Anteile vom Bezugssystem unabhängig ist. Dies ist nicht selbstverständlich, da die Stufenfunktion die Zeitkoordinate auszeichnet.
Zum Schluss extrahieren wir noch eine wichtige Abstandsskalierung. Wir betrachten
δ (1) (η(z, z)) = δ (1) (z 0 )2 − h~z, ~zi = δ (1) (z 0 )2 − r2
| {z }
≡r 2
Das Argument der δ-Distribution verschwindet für
z 0 = ±r
Aus dem Transformationsverhalten dieser Distribution folgt
o
1 n (1) 0
δ (1) (η(z, z)) =
δ (z − r) + δ (1) (z 0 + r)
2r
Aufgabe: Zeigen Sie dies.
Als Ergebnis unserer heuristischen Überlegungen notieren wir:
1
δ (1) x0 − y 0 − |~x − ~y |
4π|~x − ~y |
1
+ θ(y 0 − x0 )
δ (1) y 0 − x0 − |~x − ~y |
4π|~x − ~y |
G(x − y) = θ(x0 − y 0 )
Aufgabe: Interpretieren Sie dieses Skalierungsverhalten.
Wir wenden uns nun der inhomogenen Wellengleichung
Aµ (x) = −J µ (x) , ∂λ Aλ (x) = 0
5
Lösungstheorie
52
~ unter Lorentz-Eichung zu.
für die Potentiale (Φ, A)
Wir nehmen vereinfacht an, dass J die einzige Stromdichte in M4 ist. Wie oben argumentieren wir, dass A = f [J]
ein lineares Funktional der Stromdichte ist. Dies motiviert folgenden Ansatz:
Z
Aµ [J](x) =
d4 y Gµλ (x, y)J λ (y)
M4
Einsetzen in die inhomogene Wellengleichung unter Lorentz-Eichung liefert
x Gµλ (x, y) = −η µλ δ (4) (x − y) , ∂µ Gµλ (x − y) = 0
Es ist klar, dass Gµλ ∼ η µλ + · · · , denn die Komponenten von A mischen ja nicht in der Bewegungsgleichung.
Nun können wir aber prinzipiell zu η einen Operator addieren, der J in seinem algebraischen Kern hat. Wir
verallgemeinern:
x Gµλ (x, y) = −P µλ δ (4) (x − y) , ∂µ Gµλ (x, y) = 0
Im Fourier-Raum bedeutet dies
e µ (k) = −Peµ (k) , kµ G
e µ (k) = 0
−η(k, k) G
λ
λ
λ
µ
e
e µ (k) = P λ (k) , kµ Peµ (k) = 0
⇒G
λ
λ
η(k, k)
Damit handelt es sich bei Pe(k) um die Fourier-Darstellung des transversalen Projektors,
k µ kλ
Peµλ (k) = η µλ −
η(k, k)
Als Zwischenergebnis halten wir fest:
e µ (k)
G
λ
=
η µλ −
kµ kλ
η(k,k)
η(k, k)
Wir setzen dies in unseren Ansatz ein:
Z
Z
Z
Z
d4 q iq·(x−y) e µ
d4 k ik·y eλ
Aµ [J](x) =
d4 y Gµλ (x, y)J λ (y) =
d4 y
e
G
(q)
e J (k)
λ
(2π)4
(2π)4
M4
M4
Z
Z
Z
d4 q iq·x e µ
d4 k eλ
=
e
G
(q)
J
(k)
d4 y ei(k−q)·y
λ
(2π)4
(2π)4
M4
|
{z
}
Z
d4 q iq·x e µ
(2π)4 δ (4) (k−q)
λ
e
=
e
G λ (q) J (q)
(2π)4
µ
Z
q µ qλ
d4 q iq·x η λ − η(q,q) eλ
e
J (q)
=
(2π)4
η(q, q)
Z
Z
Z
d4 q iq·x η µλ eλ
d4 q eiq·x
e
η q, J(q)
=0 → =
e
J
(q)
=
d4 y e−iq·y J µ (y)
(2π)4
η(q, q)
(2π)4 η(q, q) M4
Z
Z
Z
d4 q eiq·(x−y)
=
d4 y G(x − y) J µ (y)
=
d4 y J µ (y)
4 η(q, q)
(2π)
4
4
M
M
|
{z
}
=: G(x−y)
Also finden wir
µ
Z
A [J](x) =
d4 y G(x − y) J µ (y)
M4
mit
x G(x − y) = −δ (4) (x − y)
5
Lösungstheorie
53
Unsere Mühen während der heuristischen Betrachtung der inhomogenen Wellengleichung für ein Skalarfeld haben
sich damit gelohnt. Es bleibt unsere Heuristik analytisch zu untermauern.
Wir wissen bereits, dass
Z
1
d4 k iη(k,x) e
e
G(x) =
e
G(k) , G(k)
=
(2π)4
η(k, k)
Die Fourier-Transformation war nützlich, da die Fourier-Amplitude einer algebraischen Gleichung genügt, und
damit das Problem G = −δ bequem auf Integration reduziert wurde. Es ist
Z
G(x) = −
R
3
Z
=−
R
3
0
dk0 e−ik0 x
R 2π (k0 )2 − |~k|2
(
)
Z
~
d3 k eihk,~xi
dk0 −ik0 x0
1
1
e
−
(2π)3 2|~k| R 2π
k0 − |~k| k0 + |k|
|
{z
}
d3 k ih~k,~xi
e
(2π)3
Z
=: I(|~
k|,x0 )
Der Integrand von I(|~k|, x0 ) hat zwei einfache Pole auf der reellen Achse bei k0 = ±|~k|. Dies hat zur Folge, dass
dem reellen Integral nur mit funktionentheoretischen Mitteln sinnvoll ein reeller Wert zugewiesen werden kann.
R
R
Die Idee ist zunächst, den Integrationsweg ins Komplexe zu verschieben, schematisch
→ ± i , > 0. Dies
kann aber äquivalent auch so interpretiert werden, dass die Pole ins Komplexe verschoben werden, ±|~k| → ±|~k| + i
oder ±|~k| → ±|~k| − i. Es wird so immer erreicht, dass der Integrationsweg frei von Polen ist. natürlich müssen
wir nach der Integration den Limes ε → 0+ betrachten. Die Berechnung des Integrals vereinfacht sich außerdem,
wenn wir vom Residuenkalkül Gebrauch machen können. Wir hoffen also, einen Pfad γ 0 zu finden mit folgenden
Eigenschaften:
I C (|~k|, x0
j
Z
+K
dk0 f k0j |~k|, x0j K→∞ −K 2π
(Z
)
+K Z
dk0C C ~ 0 f k0 j |k|, x j = lim
K→∞
0
2π
−K
γK
I
dk0C C ~ 0 df.
0
≡ lim
f k0 j |k|, x j , wobei γK = [−K, K] ∪ γK
geschlossen
K→∞ γ
2π
K
Z
dk0C C ~ 0 K→∞
und
f k0 j |k|, x j −→ 0
0
2π
γK
) = lim
0
? Da der Weg γK nach VorAußerdem bedeutet k0C die Komplexifizierung von k0 . Aber wie wählen wir γK
+
aussetzung geschlossen sein soll, muss er bei K =
in die komplexe Ebene einbiegen und dabei einen nicht
verschwindenden Imaginärteil entwickeln. Einschränkend fordern wir weiter, dass der Realteil der Punkte entlang
des Weges immer 5 K ∈ + sein soll. In einer geeigneten Umgebung U (K) von K besitzen die Punkte des in U (K)
0
verlaufenden Wegstückes dann folgende Polardarstellung: Für k0C ∈ γK
∩ U (K) gilt
R
R
k0C = A(K) eiϕ
wobei A(K) ∈
R+ ,
ϕ ∈ [−δ, +δ] ,
R+ 3 δ 1. Dann ist k0C = A(K)(1 + iϕ) + O(δ2 )
Daraus folgt
C x0
e−ik0
0
≈ e−iA(K)x e+A(K)ϕx
0
0
Das Wegintegral entlang γK
verschwindet sicherlich, wenn für fixiertes x0 gilt:
e+A(K)ϕx
0
K→∞
−→ 0
5
Lösungstheorie
54
Aus unserer lokalen Betrachtung lernen wir aber noch mehr. Für x0 < 0 muss ϕ > 0 gewählt werden, und für
x0 > 0 muss ϕ < 0 gewählt werden, also
x0 > 0 : Pole bei ± |~k| − i
x0 < 0 : Pole bei ± |~k| + i
0
Entlang γK
wählen wir einfach A(K) = K, so dass γK0 einen großen Halbkreis mit Radius K in der oberen Halbebene für x0 > 0 ist, und entsprechend für x0 < 0.
Im Grenzübergang → 0+ gilt dann
2πi
0
0
0
~
~
(−2i) sin |k|x
I(|k|, x ) = θ(+x ) −
2π
2πi
0
0
~
+ θ(−x ) +
(−2i) sin |k|x
2π
Einsetzen in G(x) auf Seite 53 liefert
G(x) = Gret (x) + Gav (x) ,
Gret (x) = +θ(+x0 )
av
0
G (x) = −θ(−x )
3
Z
Z
d k ih~k,~xi
e
(2π)3
d3 k ih~k,~xi
e
(2π)3
sin |~k|x0
|~k|
sin |~k|x0
|~k|
Nun ist
h~k, ~xi = |~k||~x| cos ^(~k, ~x)
| {z }
=:ϑ
Wir rechnen weiter:
Z +∞
Z 1
1
~
~k||~k| sin |~k|x0
d|
d cos(ϑ)ei|k|~x| cos ϑ
(2π)2 0
−1
Z +∞
θ(x0 ) 2
~k| sin |~k|x0 sin |~k||~x|
d|
=
(2π)2 |~x| 0
Z
1 θ(x0 ) +∞ ~
~k|x0 sin |~k||~x|
=
d|
k|
sin
|
(2π)2 |~x| −∞
Z +∞
n ~ 0
o
0
1 θ(x0 ) 2
~
=
d|~k| ei|k|(x +|~x|) − ei|k|(x −|~x|)
2
2
(2π) |~x| (2i) −∞
n
o
1 θ(x0 ) 2
2π δ (1) x0 + |~x| − δ (1) x0 − |~x|
=
2
2
(2π) |~x| (2i)
1 1 (1) 0
= θ(x0 )
δ
x − |~x|
4π |~x|
1
=
θ(x0 ) δ (1) (η(x, x))
2π
Gret (x) = θ(x0 )
Aufgabe: Berechnen Sie Gad