Übungsaufgaben zur Vorbereitung der Klassenarbeit

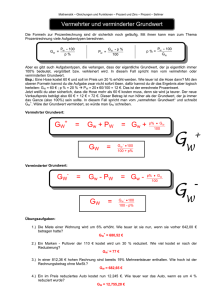
Übungsaufgaben zur Vorbereitung der Klassenarbeit Prozentrechnung
(die Lösungen mit Lösungshinweisen findet Ihr ab Seite 2)
1. Übertrage die Tabelle und ergänze!
Prozentsatz
11,5%
Grundwert
480
17,8%
Prozentwert
9,93%
12000
63
27000
750
7850
990
2. In einem Sportverein sind 261 Mitglieder. Die Vereinsstatistik weist folgende
Altersverteilung auf:
00 - 10 Jahre:
11 - 20 Jahre:
21 - 30 Jahre:
31 - 40 Jahre:
46 Mitglieder
86 Mitglieder
62 Mitglieder
33 Mitglieder
Der Rest der Mitglieder ist älter als 40 Jahre.
a) Gib die Altersverteilung in Prozent an! (Runde auf Zehntel!)
b ) Veranschauliche die Altersverteilung in einem Kreisdiagramm!
3. Lindenblüten verlieren beim Trocknen 74% ihrer Masse. Wie viel getrocknete
Lindenblüten erhält man aus 350 kg frischen Lindenblüten?
4. Nach Abzug eines Rabattes (Preisnachlass) muss Frau Reichenbach für ein Fernsehgerät
statt 2 340 Euro nur noch 2 176, 20 Euro bezahlen.
Wie viel Prozent betrug der Rabatt?
5. Herr Glück hat von seinem Lottogewinn bereits 24% ausgegeben. Es bleiben ihm noch
950 Euro.
Wie hoch war der Gewinn?
6. Ein Automechaniker kauft ein gebrauchtes Fahrzeug zu 40% des Neuwertes. Er richtet es
her und baut einen Austauschmotor ein. Dann schlägt er auf den Betrag, zu dem er das
Auto gekauft hat, 65% auf und verkauft es zu einem Preis von 7500 Euro.
Berechne den Neuwert des Autos!
Lösungen und Lösungshinweis
Hinweis: / bedeutet Bruchstrich, * bedeutet Malzeichen
1. Übertrage die Tabelle und ergänze!
Hinweis:
Führt zunächst einen Überschlag im Kopf durch. z.B. erste Spalte 10% = der Zehnte
Teil von 500 sind 50.
Hier kann man entweder den Dreisatz anwenden oder die Werte direkt mit dem
Taschenrechner.
Beispiel Dreisatz für die 2. Spalte:
63 ≙ 17,8%
63/17,8% ≙ 1%
63/17,8% * 100 ≙ 100%
354 ≙ 100%
Der Taschenrechner zeigt hier 353,9325… an. Da 17,8% mit drei genauen Stellen
angegeben ist, runden wir das Ergebnis ebenfalls auf drei genaue Stellen.
Beispiel schnelle direkte Berechnung
(dritte Spalte): 750/12000*100=
(vierte Spalte): 0,0993 * 27000 =2681,1
9,93% (drei genau Stellen), deshalb
Ergebnis auf drei genaue Stellen gerundet
Prozentsatz
11,5%
17,8%
6,25%
9,93%
12,6%
Grundwert
480
354
12000
27000
7850
Prozentwert
55,2
63
750
2680
990
3. In einem Sportverein sind 261 Mitglieder. Die Vereinsstatistik weist folgende
Altersverteilung auf:
00 - 10 Jahre:
11 - 20 Jahre:
21 - 30 Jahre:
31 - 40 Jahre:
über 40 Jahre
46 Mitglieder (17,6%)
86 Mitglieder (33,9%)
62 Mitglieder (23,8%)
33 Mitglieder (12,6%)
34 Mitglieder (13,0%)
Der Rest der Mitglieder ist älter als 40 Jahre.
a) Gib die Altersverteilung in Prozent an! (Runde auf Zehntel!)
Zunächst ist die Anzahl der Mitglieder über 40 Jahre zu berechnen.
Gesamtmitglieder – Mitglieder (0-40 J.): 261 -227= 34.
Jetzt können die prozentualen Anteile berechnet werden. Der schnellste Weg führt
über Berechnung der Anteile mit dem Taschenrechner. Ich rechne hier immer nur
den Prozentwert/Grundwert. Das Ergebnis multipliziere ich im Kopf mit 100(einfach
zwei Kommastellen nach rechts verschieben).
Beispiel: 46/261=0,1762.. Komma um zwei nach rechts und runden: 17,6%.
Hinweis: Durch Rundungsfehler kommt es dazu, dass die Summe der Anteile nicht
exakt 100% ergibt.
b ) Veranschauliche die Altersverteilung in einem Kreisdiagramm!
Hinweis: Bitte darauf achten, dass die Kreissegmente der Größe nach geordnet
eingezeichnet werden.
5. Lindenblüten verlieren beim Trocknen 74% ihrer Masse. Wie viel getrocknete
Lindenblüten erhält man aus 350 kg frischen Lindenblüten?
Nach dem Trocknen bleiben 100%-74%=26% der ursprünglichen Masse erhalten.
0,26 * 350 kg = 91kg
Man erhält 91kg getrocknete Blüten.
6. Nach Abzug eines Rabattes (Preisnachlass) muss Frau Reichenbach für ein Fernsehgerät
statt 2340 Euro nur noch 2176,20 Euro bezahlen.
Wie viel Prozent betrug der Rabatt?
Lösung:
Der ursprüngliche Preis (2340€) ist hier der Grundwert.
Da wir jetzt nach dem Prozentsatz suchen, muss hier zunächst beim Dreisatz nach dem
Prozentsatz für ein Euro gesucht werden.
2340 € ≙ 100%
1 € ≙ 100%/2340
2176,20 € ≙ 100%/2340 * 2176,2 = 93%
Eine andere Vorgehensweise:
Man bestimmt die Differenz zwischen altem und neuem Preis und rechnet dazu den Prozentsatz
aus.
Der Preis wurde um 163,80 € gesenkt.
2340 € ≙ 100%
1 € ≙ 100%/2340
163,80 € ≙ 100%/2340 * 163,80 = 7%
Der Rabatt beträgt 7%.
6. Herr Glück hat von seinem Lottogewinn bereits 24% ausgegeben. Es bleiben ihm noch
950 Euro.
Wie hoch war der Gewinn?
Lösung: Der verbleibende Teil entspricht 100% - 24% = 76%. Die Höhe des Gewinns ist der
Grundwert.
950 € ≙ 76%
Der Gewinn beträgt 1250 €.
7. Ein Automechaniker kauft ein gebrauchtes Fahrzeug zu 40% des Neuwertes. Er richtet es
her und baut einen Austauschmotor ein. Dann schlägt er auf den Betrag, zu dem er das
Auto gekauft hat, 65% auf und verkauft es zu einem Preis von 7500 Euro.
Berechne den Neuwert des Autos!
Lösung:
Um sich den Sachverhalt klar zu machen,
empfehle ich die Anfertigung einer Skizze.
Diese Aufgabe muss man „rückwärts“ lösen.
Die erste Frage lautet: Wie hoch ist der
Kaufpreis?
Wir wissen:
7500€ sind der Kaufpreis plus 65%. Der
Kaufpreis ist 100%.
7500€ ≙ 165%
7500€/165% ≙ 1%
7500/165*100€ ≙ 100%
Der Kaufpreis beträgt rund 4545,45 €. (Hinweis: Dieser Preis ist nicht sehr
praxisnah. Ein Preis von 4500 oder 4600 wäre realistischer.)
Da der Kaufpreis 40% des Neupreises (=100%) entspricht können wir jetzt diesen
berechnen:
4545,45 € ≙ 40%
4545,45 €/40 ≙ 1%
4545,45 €/40 * 100 ≙ 100%
Der Neupreis beträgt 11363,63 €.