Nachtrag zu Mittelwerten und Maßen der Dispersion Normalverteilung

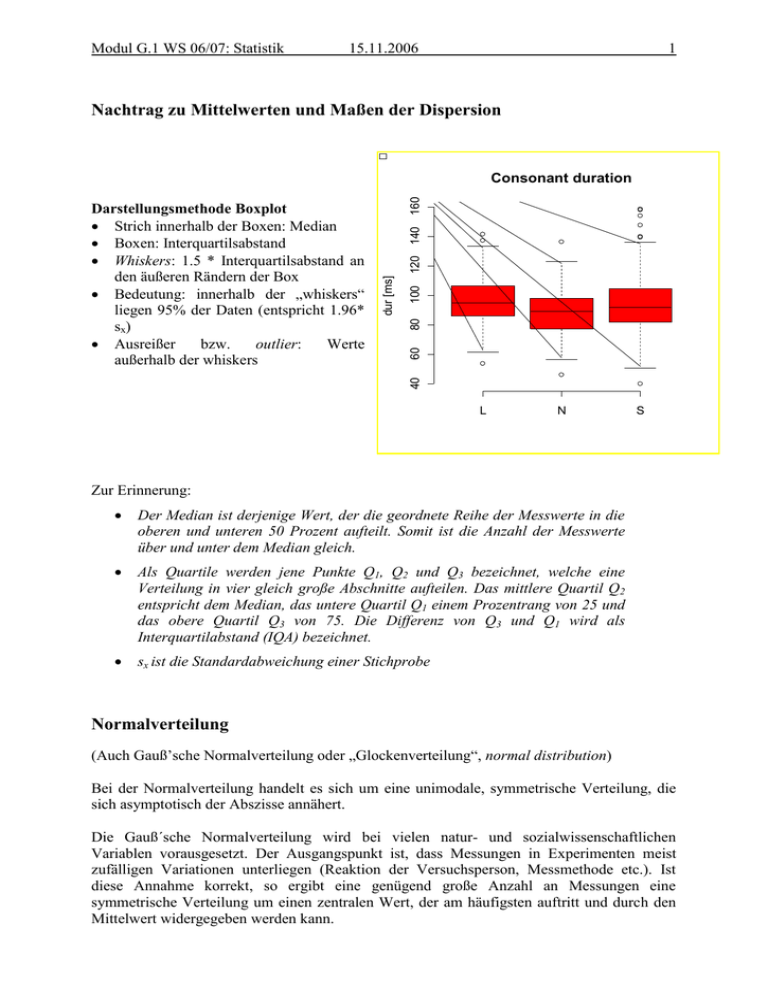
Modul G.1 WS 06/07: Statistik
15.11.2006
1
Nachtrag zu Mittelwerten und Maßen der Dispersion
120 140
100
80
60
40
dur [ms]
Darstellungsmethode Boxplot
 Strich innerhalb der Boxen: Median
 Boxen: Interquartilsabstand
 Whiskers: 1.5 * Interquartilsabstand an
den äußeren Rändern der Box
 Bedeutung: innerhalb der „whiskers“
liegen 95% der Daten (entspricht 1.96*
sx)
 Ausreißer
bzw.
outlier:
Werte
außerhalb der whiskers
160
Consonant duration
L
N
S
Zur Erinnerung:

Der Median ist derjenige Wert, der die geordnete Reihe der Messwerte in die
oberen und unteren 50 Prozent aufteilt. Somit ist die Anzahl der Messwerte
über und unter dem Median gleich.

Als Quartile werden jene Punkte Q1, Q2 und Q3 bezeichnet, welche eine
Verteilung in vier gleich große Abschnitte aufteilen. Das mittlere Quartil Q2
entspricht dem Median, das untere Quartil Q1 einem Prozentrang von 25 und
das obere Quartil Q3 von 75. Die Differenz von Q3 und Q1 wird als
Interquartilabstand (IQA) bezeichnet.

sx ist die Standardabweichung einer Stichprobe
Normalverteilung
(Auch Gauß’sche Normalverteilung oder „Glockenverteilung“, normal distribution)
Bei der Normalverteilung handelt es sich um eine unimodale, symmetrische Verteilung, die
sich asymptotisch der Abszisse annähert.
Die Gauß´sche Normalverteilung wird bei vielen natur- und sozialwissenschaftlichen
Variablen vorausgesetzt. Der Ausgangspunkt ist, dass Messungen in Experimenten meist
zufälligen Variationen unterliegen (Reaktion der Versuchsperson, Messmethode etc.). Ist
diese Annahme korrekt, so ergibt eine genügend große Anzahl an Messungen eine
symmetrische Verteilung um einen zentralen Wert, der am häufigsten auftritt und durch den
Mittelwert widergegeben werden kann.
Modul G.1 WS 06/07: Statistik
15.11.2006
2
Johnson (2004, p.14) beschreibt diese mittlere Tendenz als das zugrundeliegende Merkmal,
das wir bei Experimenten herausfinden wollen, das aber durch zufällige Fehler „verfälscht“
wird. Für die zufälligen Fehler gilt, dass die größeren Abweichungen seltener auftreten,
weshalb sich die Verteilung zu den Rändern hin an null annähert.
Die besondere Bedeutung der Normalverteilung beruht unter anderem auf dem zentralen
Grenzwertsatz, der besagt, dass eine Summe von n unabhängigen, identisch verteilten
Zufallsvariablen im Grenzwert
normalverteilt ist. Das bedeutet, dass man
Zufallsvariablen dann als normalverteilt ansehen kann, wenn sie durch Überlagerung einer
großen Zahl von Einflüssen entstehen, wobei jede einzelne Einflussgröße einen im Verhältnis
zur Gesamtsumme unbedeutenden Beitrag liefert.
Beispiel:
Auf einer Hühnerfarm mit sehr vielen Hühnern werden eine Woche lang die einzelnen Eier
gewogen. Definieren wir die Zufallsvariable X: Gewicht eines Eis in Gramm. Es stellt sich
heraus, dass ein Ei im Durchschnitt 50 g wiegt. Der Erwartungswert EX (oder auch µ) ist
daher 50. Außerdem sei bekannt, dass die Varianz s2(x) = 25 g2 beträgt. Man kann die
Verteilung des Gewichts annähernd wie in der Grafik darstellen. Man sieht, dass sich die
meisten Eier in der Nähe des Erwartungswerts 50 befinden und dass die Wahrscheinlichkeit,
sehr kleine oder sehr große Eier zu erhalten, sehr klein wird. Wir haben hier eine
Normalverteilung vor uns. Sie ist typisch für Zufallsvariablen, die sich aus sehr vielen
verschiedenen Einflüssen zusammensetzen, die man nicht mehr trennen kann, z.B. Gewicht
des Huhns, Alter, Gesundheit, Standort, Vererbung usw.
Die Normalverteilung ist symmetrisch bezüglich μ. Die Verteilung P(X ≤ a) von X ist die
Fläche unter dem Graph der Dichtefunktion. Sie wird bezeichnet als
Beispielsweise beträgt die Wahrscheinlichkeit, dass ein Ei höchstens 55 g wiegt, 0,8413. Das
entspricht der roten Fläche in der Abbildung.
Modul G.1 WS 06/07: Statistik
15.11.2006
3
Mit Standardabweichung = 𝜎 und Erwartungswert = µ
Der Erwartungswert (selten und doppeldeutig Mittelwert) ist ein Begriff der Stochastik. Der
Erwartungswert μ einer Zufallsvariablen (X) ist jener Wert, der sich (in der Regel) bei
oftmaligem Wiederholen des zugrunde liegenden Experiments als Mittelwert der Ergebnisse
ergibt. Er bestimmt die Lokalisation (Lage) einer Verteilung und ist vergleichbar mit dem
empirischen arithmetischen Mittel einer Häufigkeitsverteilung in der deskriptiven Statistik.
Das Gesetz der großen Zahlen sichert in vielen Fällen zu, dass der Stichprobenmittelwert bei
wachsender Stichprobengröße gegen den Erwartungswert konvergiert.
Eigenschaften:
 Datenreduktion: Mit den beiden Kenngrößen μ und σ kann die Wahrscheinlichkeit für das
Auftreten einzelner Messwerte vorhergesagt werden.
 Die Fläche unterhalb der Kurve ist immer 1, d.h. Normalverteilungen mit einem
Mittelwert, der eine geringe Häufigkeit aufweist, haben eine große Standardabweichung
(„flach und breit“) und umgekehrt („spitz und schmal“)
 Dichte (density): gibt die Wahrscheinlichkeit an, dass ein Maß sehr nah an einem
Messwert liegt. Wahrscheinlichkeiten liegen zwischen 0 und 1 mit steigender
Wahrscheinlichkeit. Durch die Definition der Funktionsgleichung ist es möglich, das
Integral, die Fläche, unter der Kurve, zu berechnen. Mit dieser Fläche kann man die
Intervalle bestimmen, in denen gewisse Prozentanteile der Stichprobe mit hoher
Wahrscheinlichkeit enthalten sind. Eine Dichtefunktion, Wahrscheinlichkeitsdichte oder
Wahrscheinlichkeitsdichtefunktion (WDF oder pdf von engl. probability density function)
dient in der Mathematik der Beschreibung von Wahrscheinlichkeitsverteilungen
 Bei normalverteilten Daten liegen 68,28% der Daten innerhalb eines Bereiches von ±
1Standardabweichung und 95,44 % im Bereich von ± 2 SD
 Im statistischen Sinne normale Daten liegen zwischen -1,96 * SD und +1,96*SD. Alle
außerhalb dieser 95% Marke liegenden Daten sind Ausreißer.
Modul G.1 WS 06/07: Statistik
15.11.2006
4
Die Wahrscheinlichkeiten der einzelnen Ausprägungen einer stetigen Zufallsvariablen können
(im Gegensatz zum diskreten Fall der Wahrscheinlichkeitsfunktion) nicht angegeben werden,
denn die Wahrscheinlichkeiten für jede einzelne Ausprägung müssen streng genommen 0
gesetzt werden. Es lassen sich nur Wahrscheinlichkeiten f(x)dx dafür angeben, dass die Werte
innerhalb eines Intervalls dx um x liegen. Die Funktion f(x) heißt dann Dichtefunktion. Die
Wahrscheinlichkeit, dass die Zufallsvariable Werte zwischen a und b annimmt, wird dann
allgemein definiert als das Integral über diese Funktion mit den Integrationsgrenzen a und b.
Beispielsweise fragt man nicht, wie viele Personen exakt 1,75 Meter groß sind, sondern z. B.,
wie viele Personen zwischen 1,75 und 1,76 m groß sind. Denn die Wahrscheinlichkeit, dass
eine Person auf beliebig viele Nachkommastellen genau 1,75 Meter groß ist, ist theoretisch
und praktisch gleich Null (daraus folgt: Nullmenge).
Beispiel:
Der HAWIE (Hamburg-Wechsler-Intelligenztest für Erwachsene) besitzt einen Mittelwert
von 𝒙 = 100 IQ-Punkte und eine Standardabweichung von sx=15 Punkten. Dies bedeutet, dass
4,56% der Bevölkerung einen IQ von unter 70 oder über 130 Punkten haben.
Abweichungen von der Normalverteilung
0.008
0.006
0.004
0.002
Density
0.010
0.012
1. Mehrere Gipfel (bimodal bis multimodal)
bedeutet meist, dass die Quelle der Variation nicht zufällig ist, z.B. Vokaldauern, wenn Kurzund Langvokale in einem Datensatz analysiert werden.
60
80
100
120
Vokaldauer [ms]
140
160
180
Modul G.1 WS 06/07: Statistik
15.11.2006
5
2. Asymmetrie (skewness)
Achtung: linkssteil = rechtsschief, rechtsteil = linksschief
Die Schiefe wird mit dem zentralen Moment dritter Ordnung berechnet. Als zentrales
Moment wird die Differenz eines individuellen Werts vom Mittelwert bezeichnet:
(xi - 𝑥 )a
Der Exponent a bestimmt die Ordnung des zentralen Moments.
a3=0: Symmetrie
a3<0: rechtssteil
a3>0: linkssteil
Modul G.1 WS 06/07: Statistik
3. „Gipfeligkeit“, Exzess, Breite
a4=3: normal
a4<3: platykurtisch (breit)
a4>3: leptokurtisch (spitz)
15.11.2006
6
Modul G.1 WS 06/07: Statistik
15.11.2006
Rechenbeispiel zur Schiefe und Gipfeligkeit einer Verteilung
7
Modul G.1 WS 06/07: Statistik
15.11.2006
8
Normierung
Wichtig ist, dass die gesamte Fläche unter der Kurve gleich 1 ist, also der Wahrscheinlichkeit
eines fast sicheren Ereignisses entspricht. Somit folgt, dass, wenn zwei gaußsche
Glockenkurven dasselbe μ, aber unterschiedliche σ-Werte haben, jene Kurve mit dem
größeren σ breiter und niedriger ist (da ja beide zugehörigen Flächen jeweils den Wert von 1
haben und nur die Standardabweichung (oder „Streuung“) höher ist). Zwei Glockenkurven
mit dem gleichen σ, aber unterschiedlichen μ haben gleich aussehende Graphen, die jedoch
auf der x-Achse um die Differenz der μ-Werte zueinander verschoben sind.
Standardnormalverteilung und die z-Transformation
Die Standardnormalverteilung hat einen Mittelwert von 0 und eine Standardabweichung von
1.
Modul G.1 WS 06/07: Statistik
15.11.2006
9
Dichtefunktion der Standardnormalverteilung
Eigenschaften der z-Verteilung: Die Fläche ist wiederum 1 bzw. 100%.
Transformation zur Standardnormalverteilung (z-Transformation)
Ist eine Normalverteilung mit beliebigen μ und σ gegeben, so kann diese durch eine
Transformation auf eine
-Normalverteilung zurückgeführt werden.
Die Überführung geschieht durch die z-Transformation in die sogenannten z scores.
zi=(xi-𝑥)/sx
Geometrisch betrachtet entspricht die durchgeführte Substition einer flächentreuen
Transformation der Glockenkurve von
zur Glockenkurve von
.
Durch die z-Transformation können sämtliche Normalverteilungen standardisiert werden,
d.h. auf einen Standard gebracht werden. Wir bezeichnen deshalb die Normalverteilung
mit μ= 0 und σ=1 als Standardnormalverteilung.
Modul G.1 WS 06/07: Statistik
15.11.2006
10
(vgl. Bortz, 5. Auflage, S. 75, vgl. Übungsaufgabe zur z-Transformation)
Wichtige Anwendung in der Phonetik: Sprechernormalisierung
Problem: Formanten sind nicht nur von der Vokalqualität sondern auch von sprecherspezifischen Merkmalen des Ansatzrohres abhängig.
Lösung:
1. z-Transformation mit sprecherspezifischen Mittelwerten und Standardabweichungen =
Lobanov-Transformation
Fn.norm=(Fn-Fn.mean)/Fn.sd
Fn.norm wird für jeden einzelnen Sprecher berechnet.
n entspricht jeweils dem n-ten Formanten (F1, F2 etc.)
2. Daten werden auf den maximalen Range der einzelnen Sprecher normalisiert =
Gerstman-Transformation
Fn.norm=(Fn-Fn.min)/(Fn.max-Fn.min)
(vgl. Harrington & Cassidy (1999) S. 76-78)